基于粒度和信息熵的并行支持向量机算法
2021-05-14毛伊敏张刘鑫卢欣荣
毛伊敏, 张刘鑫, 卢欣荣
(1.江西理工大学信息工程学院, 赣州 341000; 2.江西理工大学应用科学学院, 赣州 341000)
支持向量机(support vector machine, SVM)算法是数据挖掘和机器学习的常用方法之一,其以结构风险最小化为准则设计学习模型,具有较好的鲁棒性;利用核函数将样本数据映射到高维特征空间,避免了“维度灾难”;将原问题转化为凸二次规划问题,求解目标函数可以获得全局最优解[1]。因此,支持向量机算法被广泛应用于图像分析[2]、目标检测[3]、生物医学[4]等各种领域。
随着信息技术的快速发展以及大数据时代的来临,大数据相较于传统数据具有了Volume(数量大)、Veracity(准确性)、Variety(种类多)、Velocity(速度快)、Value(价值密度低)的“5V”特性[5]。但是传统的支持向量机所需的时间复杂度较高,只适用于较小规模的数据集,而在处理大数据时,无疑会产生巨额的计算复杂度[6]。所以,如何降低支SVM算法的计算复杂度并提高其执行效率、使其能够处理大数据是个关键性的难题。
随着Google开发的MapReduce架构的广泛应用,以Hadoop、Spark为代表的分布式计算架构受到了越来越多的关注[7-9]。为了能进一步降低SVM算法的计算复杂度,通过改进传统的支持向量机算法,并与分布式的计算架构结合成为当前支持向量机算法的研究热点。Alham等[10]提出了基于MapReduce和Bagging的并行集成支持向量机算法(MapReduce-based distributed SVM ensembles algorithm,MRESVM),该算法利用MapReduce计算模型在Hadoop平台上并行训练SVM,在保证分类精度的同时有效地提高了算法的执行效率,但是,随着训练样本的增大,算法的运行时间会迅速增长。在此基础上,Kun等[11]提出了并行组合支持向量机算法(parallel sequential minimal optimization,PSMO),为解决支持向量机处理大规模数据时执行效率低的问题,该算法将原始数据集划分成规模较小的子数据集,在每个子数据集上训练SVM模型,合并所有局部支持向量并单独训练支持向量机得到最终分类模型,实验结果分类准确度不高。为了进一步提高算法的性能,丁萱萱等[12]提出了基于MapReduce和Bagging的并行组合支持向量机算法(parallel recombined SVM ensembles algorithm,PRESVM),该算法首先采用分组训练的方式删除大部分的非支持向量,缩小训练集的规模,然后利用随机梯度下降算法加快SVM的训练过程,实验表明该算法的执行效率得到了提高。然而,这些算法都未有效识别和删除噪声数据,导致大数据环境下算法的分类准确度较低。
如何解决并行支持向量机算法的噪声数据较敏感问题,并提高大数据环境下算法的分类准确度,一直是并行SVM算法的重要研究内容。为了解决这个问题,Fan等[13]提出了基于概率推理的分布式支持向量机算法(distributed SVM algorithm based on probabilistic inference,PIDSVM),该算法利用概率推理方法找出隐藏在训练集中的噪声特征,并将其考虑到建模中。同时,Sarumathiy等[14]提出了基于特征提取和互信息的并行支持向量机算法(parallel SVM algorithm based on feature select and mutual information,FMPSVM),该算法有效地识别数据集中相关度较低的特征,降低了噪声数据的影响。虽然以上算法可以有效地识别和删除大数据环境下的噪声数据,避免了噪声数据成为支持向量,影响分类决策平面的构建,但是这些算法都忽略了训练样本数据冗余问题对模型训练的影响,导致算法的时间复杂度较高。针对这个问题,王瑞等[15]提出了基于K-means的分布式SVM优化算法,该算法通过聚簇的方式划分数据集,快速删除训练样本中的冗余数据,有效地加快了算法的执行效率。除此之外,Hu等[16]提出了一种基于MapReduce的并行迭代SVM算法(parallel iterative SVM algorithm based on cuckoo search,PISVM-CS),该算法利用布谷鸟算法优化SVM的参数,以并行迭代的方式筛选类边界样本,从而得到较好的分类模型。虽然目前基于MapReduce的并行支持向量机算法的研究已经取得了一些成果,但如何有效地识别并删除大数据环境下的噪声数据,从而提高算法的分类精度,如何迅速删除冗余的训练样本集,降低算法的时间复杂度,仍是当前亟需解决的问题。
针对以上问题,提出基于粒度和信息熵的(the SVM algorithm by using granularity and information entropy based on MapReduce,GIESVM-MR)算法。主要工作为:①提出噪声清除策略(noise cleaning, NC)对每个特征属性的重要程度进行评价,获得样本与类别之间的相关度,以达到识别和删除噪声数据的目的;②提出基于粒度的数据压缩策略(data compression based on granulation, GDC),通过筛选信息粒的方式来保留类边界样本删除非支持向量,获得规模较小的数据集,从而解决了大数据环境下训练样本数据冗余问题;③结合Bagging的思想和MapReduce计算模型并行化训练SVM,生成最终的分类模型。实验表明,GIESVM-MR算法的分类效果更佳,且在大规模的数据集下算法的执行效率更高。
1 相关概念介绍
1.1 信息熵
对于一个离散型的变量X,其信息熵[17]为
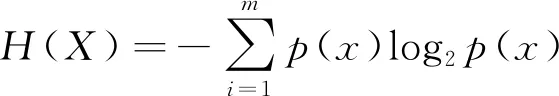
(1)
式(1)中:p(x)为离散变量X在系统事件中出现的概率。
1.2 粒度支持向量机
粒度支持向量机是由Tang等[18]最先提出来的,给定一个数据集D={x1,x2,…,xn},可以以某种方式构建粒度空间,信息粒可以表示为
G={g1,g2,…,gm}
(2)
式(2)中:m为信息粒的个数。
2 GIESVM-MR算法
GIESVM-MR算法主要包括3个阶段:噪声过滤、数据压缩和并行SVM模型构建。
(1)在噪声过滤阶段:提出了噪声清除策略NC对每个特征属性的重要程度进行评价,获得样本与类别之间的相关度,有效地识别和删除大数据环境下的噪声数据。
(2)在数据压缩阶段:提出基于粒度的数据压缩策略GDC, 通过筛选信息粒的方式保留类边界样本删除非支持向量,获得规模较小的数据集,从而解决了大数据环境下训练样本数据冗余问题。
(3)在并行SVM模型构建阶段:结合Bagging的思想和MapReduce计算框架并行训练SVM模型,组合所有基学习器得到最终分类模型。
2.1 噪声过滤
由于大数据环境下并行SVM算法对噪声数据较敏感,当噪声数据成为支持向量,会严重影响SVM分类决策平面的构建,从而导致算法的分类准确度降低。为了解决大数据环境下并行支持向量机的噪声敏感问题,提出NC策略来识别和删除噪声数据,首先判断每个特征属性的重要程度,并以信息熵加权的方式获得属性的权值;然后结合属性权值和欧式距离公式设计信息熵加权距离公式IEWED,计算样本间的相似度;最后对样本与类别之间的相关度进行度量,识别并删除大数据环境下的噪声数据。具体步骤如下:
2.1.1 获得每个特征属性的权值
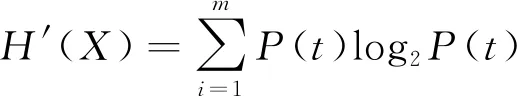
(3)
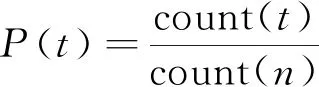
(4)
式中:t表示在类别判断中某一个特征属性的重要程度;m表示特征属性的数目;P(t)表示正类样本中属性t出现的概率;count(t)表示正类样本中属性t出现的次数,count(n)表示正类样本的数目。
证明:
(1)单调性。对于∀t1,t2且t1-t2>0,P(t1)-P(t2)>0,则H′[P(t1)]-H′[P(t2)]<0。
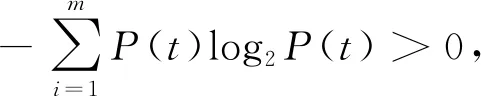
(3)累加性。对于∀t1,t2∈X,H′(X)=H′[P(t1,t2)]=H′[P(t1)·P(t2)]=H′[P(t1)]+H′[P(t2)]。
因此式(3)满足信息熵定义的基本条件,是算法稳定的度量公式。
由于每个属性的重要程度不一样,在类别判定中起的作用不同,可以利用信息熵的比值来显性地表示某个属性在类别划分中所占的权值,则基于信息熵的加权系数ωi可以表示为
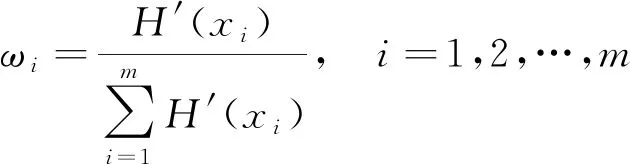
(5)
2.1.2 计算样本间的相似度
传统的欧式距离只能计算两个样本之间的线性距离,是建立在所有特征属性都同等重要的条件下[19]。然而,样本的属性不一定和类别相关联,如果样本的属性与类别相关联,其相关联程度也不一定相同,仅仅使用欧氏距离来衡量两个样本间的关联程度,没有考虑样本内不同属性与类别的相关度,加强相关联比较大的属性和减弱相关联比较小的属性能够更加准确地计算样本间相似度。因此,结合特征属性权值和欧式距离公式设计的信息熵加权的距离(IEWED)公式可以表示为
d(x,y)=
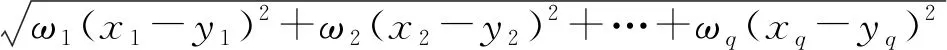
(6)
式(6)中:q为样本的特征数;x、y为数据集S={x1,x2,…,xn}中的两个样本;xq、yq分别为样本x、y第q个属性的数值。
证明:
(1)对于∀x,y∈S且x≠y,存在d(x,y)>0,非负性满足。
(2)对于∀x,y∈S,d(x,y)=d(y,x),对称性满足。
(3)对于∀x,y,z∈S,d(x,y)+d(y,z)>d(x,z),三角不等式满足。
因此式(6)满足相似性度量的以上3个特性,是相似性度量公式。
2.1.3 获取样本与类别之间的相关度
对于数据集S={x1,x2,…,xn},其中正类样例集P中样本的个数为nS+,负类样例集N中样本的个数为nS-,且nS++nS-=nS。根据中心点计算公式[20],可以设置正类样例的类中心c+和负类样例的类中心c-为
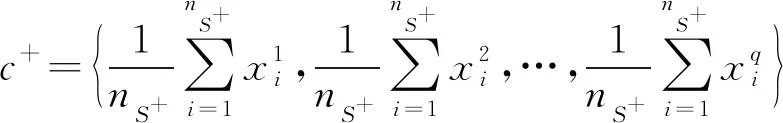
(7)
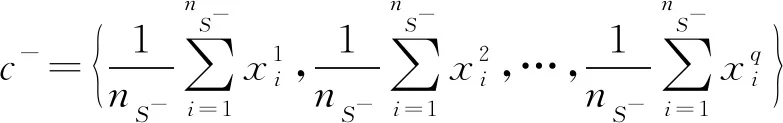
(8)
式中:q表示样本的特征数。可以根据信息熵加权的距离公式(IEWED)分别计算每个样本到正类中心和负类中心的距离d(xi,c+)和d(xi,c-),d(xi,c+)和d(xi,c-)的计算公式如下:
d(xi,c+)=
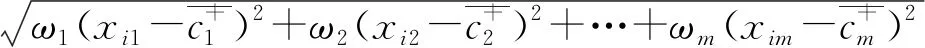
(9)
d(xi,c-)=
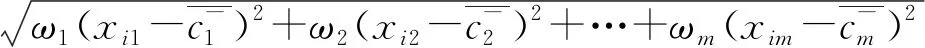
(10)
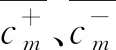
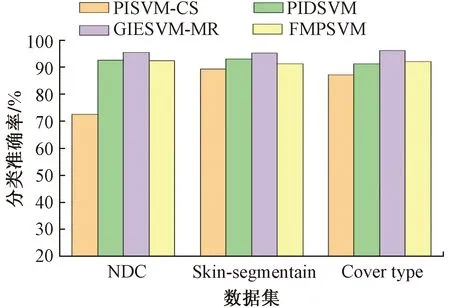
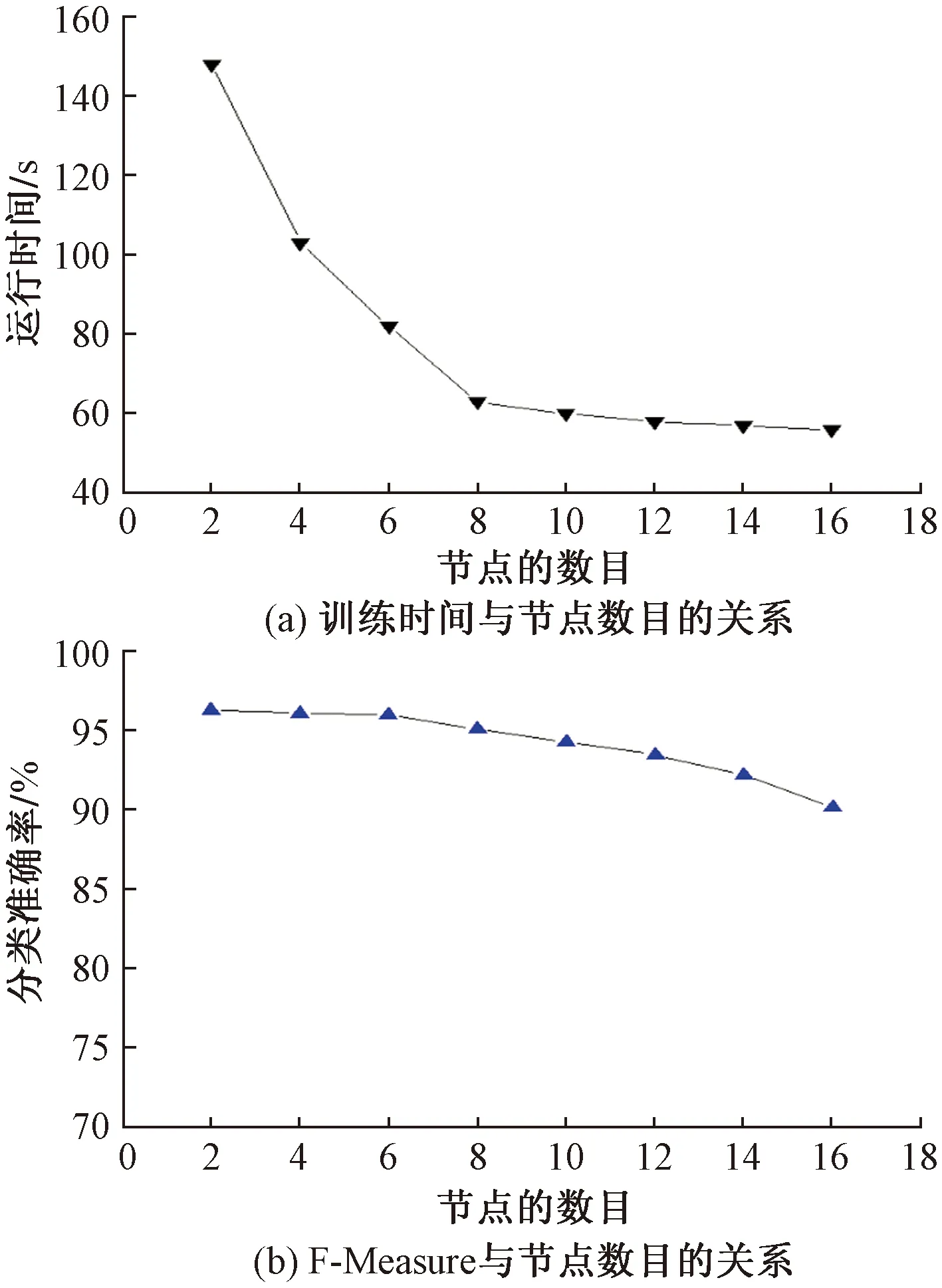
利用d(xi,c+)和d(xi,c-)表示样本与类别之间的相关联程度,对于∀xi∈P,如果d(xi,c-) NC策略的伪代码如下。 算法1 NC策略 输入:训练集S={x1,x2,…,xn} 输出:噪声过滤后的数据集set(S′) (1) Foriinndo{ (2) Calculated(xi,c+) by Eq.(9) (3) Calculated(xi,c-) by Eq.(10) (4) Ifxi∈P&&d(xi,c-) (5) Regardxias noise (6) } (7) Else if{ (8)set(S′)←xi (9) }end if (10) Ifxi∈N&&d(xi,c+) (11) Regardxias noise (12) } (13) Else if{ (14)set(S′)←xi (15) }end if (16)}end for (17)Returnset(S′) 2.2.1 获取全局支持向量 在利用NC策略识别和删除大数据环境下的噪声数据后,为了进一步降低并行SVM算法处理大规模数据的时间复杂度,需要删除训练样本中的冗余数据。对此,提出了GDC策略来删除大数据环境下的训练样本冗余数据,首先对样本特征空间进行等分,并获得划分后的信息粒;然后筛选并保留边界样本对应的信息粒,即支持向量,以此解决了训练样本数据冗余问题。具体步骤如下。 1)信息粒的划分 (11) 对于信息粒gi,用Pi表示该信息粒中正例所占的比例,Ni表示该信息粒中负例所占的比例,则信息粒gi的纯度Purityi可以表示为 Purityi=1-min(Pi,Ni) (12) 性质1对于∀gi∈G={g1,g2,…,gm},m为信息粒的个数,若Purityi=1,则表示该信息粒为纯粒,信息粒中仅有正例或负例;若Purityi∈[1/2,1),则表示该信息粒为混合粒,信息粒中同时含有正例和负例,且Purityi值越小,该信息粒混合度越高,Purityi值越大,该信息粒混合度越低。 证明: 因为Purity=1-min(Pi,Ni) 所以 当Purityi=1时,1-min(Pi,Ni)=1 则存在Pi=1,Ni=0或Pi=0,Ni=1 因此信息粒gi仅有正例或负例,即为纯粒。 所以当Purityi∈[1/2,1)时,1-min(Pi,Ni)∈[1/2,1),则min(Pi,Ni)∈(0,1/2],存在Pi≠0且Ni≠0,当且仅当Pi=Ni=1/2时Purityi=1/2,此时信息粒gi中正例和负例的数目相等,信息粒的混合度最高。因此信息粒gi中同时含有正例和负例,即为混合粒。 由性质1可知,如果某信息粒为纯粒,则该信息粒中仅有正例或负例;如果信息粒为混合粒,则该信息粒中同时含有正例和负例。由于SVM的决策平面与支持向量相关,而支持向量多为类边界样本[21]。因此可以保留混合粒中的样本,即支持向量,删除纯粒中的样本,即非支持向量。从而达到保证SVM模型分类准确度的同时迅速缩减训练集的目的,进而提高算法的执行效率。 2)信息粒的筛选 对于任一混合粒,如果信息粒中样本数目大于给定阈值ε,则对该信息粒对应特征空间的每个特征值域进行二等分。直到所有信息粒为混合粒的同时满足以上条件,则停止信息粒的划分。此时得到的信息粒都是混合粒即类边界样本,合并所有混合粒得到与原始问题近似的全局支持向量。(取ε=4)。 GDC策略的伪代码如下。 算法2GDC策略 输入:训练集D={x1,x2,…,xn},样本的特征空间维度d,停止划分阈值ε 输出:数据压缩后的数据集set(D′) (1) DivideDinto 2dgi (2) Foriin 2ddo{ (3) Calculate Purityiby Eq.(12) (4) If Purityi=1 { (5) Regardgias pure grain (6) } (7) Else if { (8) Regardgias mixture grain (9) }end if (10) While(Ngi>ε) { (12) } (14) }end for (15) Returnset(D′) 2.2.2 并行获取全局支持向量 在提出了GDC策略后,为了能更快地删除训练样本中的冗余数据,进一步加快算法的执行效率,结合MapReduce计算模型,提出并行获取全局支持向量的方法。在Split阶段,将给定的数据集划分成同等规模并存储在每个mapper节点上;在Map阶段,对每个数据块内的数据使用GDC策略筛选支持向量,删除冗余的训练数据,获得局部支持向量;在Reduce阶段,合并所有Mapper节点上得到的支持向量得到全局支持向量。并行获取全局支持向量的伪代码如下。 算法3并行获取全局支持向量 输入:数据集D={x1,x2,…,xn},节点个数T 输出:数据压缩后的数据集set(D′) (1) Split(DatasetD) (2) Divide datasetDinto same size block by Hadoop file block strategy (3) Create(MR-job) (4) Map: (5) For each mappers do (6) Obtain local SVs result by calling GDC strategy (7) Reduce: (8)set(D′)←SVs (9) Returnset(D′) 在经过数据压缩获得较小规模的数据集后,需要训练SVM模型。由于单个支持向量机模型容易产生误分类的问题,导致算法的分类准确度不高。基于Bagging的集成学习方法可以有效地克服这个问题,通过训练多个基学习器共同做决策,有效地避免了单一分类器模型出现的误差问题,加强了算法整体的稳定性[22]。为了提高算法的分类准确度,基于Bagging的思想训练多个基分类器,采用投票法获得类别划分的结果。为了进一步加快SVM模型的训练过程,提高算法的总体并行化效率,利用MapReduce计算模型并行训练支持向量机模型。在数据划分阶段,根据bootstrap自助抽样的方法获得m个与初始样本集同等规模的数据集,并分发给每个Mapper节点;在Map阶段,利用每个子数据集单独训练一个支持向量机模型,将训练得到的基学习器组合起来得到一个强的分类模型。并行SVM模型构建的伪代码如下。 算法4 并行SVM模型构建 输入:数据集D′={x1,x2,…,xn},节点个数T 输出:预测模型 (1) Split(DatasetD′) (2) Replicate datasetS′based on bootstrap and getmtraining datasets (3) Map: (4) For each Block do (5) Train SVM onmtraining datasets (6) Obtainfi(x) (7) Save the SVM model in each node of Hadoop (8) Emit PredictionModel() GIESVM-MR算法的具体实现步骤如下。 步骤1 根据输入的原始数据集,通过调用算法1的NC策略识别并删除噪声数据,得到噪声清除后的训练集; 步骤2 在数据压缩阶段,通过调用算法3并行执行GDC策略,快速获得数据压缩后的全局支持向量SVs; 步骤3 获取数据压缩后的数据集,启动MapReduce任务,调用算法4并行训练SVM模型,从而获得最终的分类模型。 GIESVM-MR算法的时间复杂度主要由噪声过滤、数据压缩、并行SVM模型构建这几个步骤构成。这些步骤的时间复杂度分别为: (1)噪声过滤阶段,设原数据集的大小为M,使用“NC”策略对数据集进行噪声样本的识别和删除,其中需要计算每个样本到正类中心和负类中心的距离,则进行噪声过滤的时间复杂度为O(M)。 (2)数据压缩阶段,设经过噪声过滤得到的样本集大小为N,样本的维度为d,则使用GDC策略进行粒度化并划分,需要对2d个信息粒进行判断,则进行数据压缩获得SVs的时间复杂度为O(2d)。 (3)并行SVM模型构建阶段,假设数据压缩后的样本集中样本数目为M′,则训练支持向量机模型的时间复杂度为O(M′3)。因此GIESVM-MR算法时间复杂度为数据压缩、噪声过滤和并行SVM模型构建的时间复杂度之和O(2d+M+M′3)。 为验证GIESVM-MR算法的性能展开了相关实验。实验的硬件设备为Master主机1台和Slaver机3台,共4个节点,每一台硬件设备的处理器均为Intel(R)Core(TM)i5-9400H CPU @ 2.9 GHz,内存16G。实验的软件编程环境均为python3.5.2;操作系统均为Ubuntu 16.04;MapReduce架构均为Apache Hadoop3.2版本。 GIESVM-MR算法采用的实验数据是来自标准UCI数据库的真实数据集,分别是NDC数据集[23]、Skin-Segmentain数据集[24]和Cover type数据集[25]。其中,NDC数据集是由正态分布集群数据发生器随机生成的数据,该数据集样本数量为100 000,维度为32,具有数据量小、噪声数据多的特点;Skin-Segmentain数据集是随机采集的人脸图像,包含不同种族、不同年龄、不同性别的数据,该数据集样本数量为245 057,维度为3,具有维度小的特点; Cover type数据集是美国地质调查局和USF记录某森林覆盖率的数据,其中包含多种植被的数据,将其划分为两类:A类植被和非A类植被,该数据集样本数目为581 012,维度为10,具有数据量大,支持向量少的特点。数据集的具体信息如表1所示。 表1 实验数据 使用F-Measure作为指标来评价算法的分类准确度,F-Measure综合考虑了分类结果的正确率(precision)和召回率(recall)的情况,能够较为准确地评价分类算法的结果,其计算公式为 通常情况下,参数λ设置为1,当F-Measure的值较高时,表示分类结果更为准确合理。 GIESVM-MR算法使用GDC策略根据特征属性将原始数据划分为信息粒,通过保留类边界样本对应的混合粒,删除对SVM模型构建没有作用的纯粒,即非支持向量,以达到删除训练样本中的冗余数据的目的,进而降低支持向量机的训练时间。但对于信息粒再划分的阈值ε来说,需要指定具体的数值,阈值ε过小,原始训练集将压缩为空集,所以阈值ε的值至少大于1,同时,如果阈值ε设置过大,不仅不能有效地识别训练集中的支持向量,而且通过GDC策略得到的训练集规模较大,导致GIESVM-MR算法的整体执行时间增加。为了加快GIESVM-MR算法执行效率的同时能获得更加准确的分类结果,需要对阈值ε的取值进行合理的设置,在基于NDC数据集下,保证其他参数不变,将阈值ε的取值设置为[2,10],重复运行10次,取10次的F-Measure平均值进行分析。从图1中可以看出,阈值ε给定的太小会影响分类结果的准确度。实验结果表明,在ε的值取4的时候,能得到准确的分类结果,并且此时利用GDC策略得到的训练集规模较小。 图1 阈值ε的选取 3.5.1 算法的时间复杂度分析 将GIESVM-MR算法分别与PIDSVM[13]、FMPSVM[14]和PISVM-CS[16]算法在NDC、Skin-Segmentain和Cover type数据集下进行对比实验,在实验中分别比较了不同数据规模下GIESVM-MR算法与PISVMAM算法和PIDSVM算法的执行时间,实验结果如图2所示。 图2 不同算法在3个数据集上的执行时间 从图2中可以明显看出,随着数据规模的增大,GIESVM-MR算法的执行时间呈线性小幅度的增长,而PIDSVM、FMPSVM和PISVM-CS算法的执行时间呈几何倍数增长。在规模较小的NDC数据集上,GIESVM-MR算法的执行时间相较于PIDSVM、FMPSVM和PISVM-CS算法分别降低了76.2%、43.7%和60.5%;随着训练数据规模的增大,在Skin-Segmentain数据集上,与PIDSVM、FMPSVM和PISVM-CS算法相比,该算法的执行时间分别降低了83%、71.2%和60%;在规模最大的Cover type数据集上,相较于PIDSVM、FMPSVM和PISVM-CS算法3种算法,GIESVM-MR算法的执行时间分别降低了82.4%、72.1%和68.4%。其主要原因是:GIESVM-MR算法使用GDC策略筛选支持向量,删除大规模数据中的冗余数据即非支持向量,以更优的方式适应了大数据环境。其中,相较于PIDSVM算法虽然利用分布式的训练方式处理大规模数据,但是每个支持向量机需要处理的数据规模还是相当庞大的,没有利用一种有效的方法来筛选支持向量,缩小原始训练集的规模,对于FMPSVM算法虽然利用特征选择的方式减少了相关度较低的特征,降低了训练样本集的维度,但是支持向量机模型的训练还是需要处理大规模的数据集,导致算法的执行时间较大。同时,PISVM-CS算法,利用遗传算法寻找最优的参数,以迭代的方式寻找支持向量,模型的训练过程中存在大量的迭代过程,多次执行MapReduce任务,增加了节点间的信息传输时间,随着训练数据集规模的增大算法的迭代寻优过程更加复杂,导致算法的训练时间急剧增长。因此,GIESVM-MR算法能够克服此类问题是因为首先将数据粒化,并根据特征空间划分成不同的信息粒,筛选类边界样本所对应的混合粒,即支持向量,迅速减小了训练集的规模,有效地提高了大数据环境下GIESVM-MR算法的执行效率。 3.5.2 算法的分类准确度分析 将GIESVM-MR算法分别与PIDSVM[13]、FMPSVM[14]和PISVM-CS[16]算法在NDC、Skin-Segmentain和Cover type数据集下进行对比实验,在实验中分别比较了GIESVM-MR算法与PISVMAM算法和PIDSVM算法的分类准确度F-Measure,实验结果如图3所示。 图3 各种算法在3个数据集上的F-Measure 从图3可以看出,GIESVM-MR算法在3个数据集上的分类准确度均较高。在噪声数据较多的NDC数据集上,GIESVM-MR算法的分类准确度相较于PIDSVM、FMPSVM和PISVM-CS算法分别提高了3.2%、3.4%和27.4%,这是因为该算法使用NC策略有效的识别并删除数据中的噪声,获得没有噪声的数据集,从而避免了噪声数据成为支持向量影响分类决策平面的确立。PIDSVM算法利用概率推理方式识别隐藏在数据集中的噪声数据,并将其考虑到模型的构建中,克服了噪声数据的干扰。同时,FMPSVM算法结合特征选择和互信息有效识别了数据集中相关度较低的特征,降低了噪声数据的影响。然而,PISVM-CS算法没有有效地识别数据集中的噪声数据,多次迭代反而会积累误差,导致分类准确度较差。在Skin-Segmentain数据集上,与PIDSVM、FMPSVM和PISVM-CS算法相比,GIESVM-MR算法的分类准确度分别提高了2.1%、4.3%和6.5%。而在数据规模最大的Cover type数据集上,GIESVM-MR算法的分类准确度比PIDSVM、FMPSVM和PISVM-CS 3种算法分别提高了5.5%、4.6%和10.4%。这是因为GIESVM-MR算法利用NC策略有效地识别和删除了噪声数据,进而提高了大数据环境下算法的分类准确度。 为了验证GIESVM-MR算法在不同节点数目下的分类准确度和训练时间, 在NDC数据集上进行10次重复实验,计算均值作为最终结果,实验结果如图4所示。 图4 GIESVM-MR算法在不同节点数目上执行时间和F-Measure 从图4(a)可以看出, GIESVM-MR算法的执行时间随着节点数的增多而迅速减少。这是由于节点数的增多,有效地提高了算法的并行化程度,减少了每个节点上的任务量,同时降低了每个节点上的训练时间,从而减小了算法整体的运行时间;但是节点数超过10以后,算法的执行时间保持在60 s左右,每个节点上的执行时间趋于平缓,节点间的信息传输时间会增加,所以算法的运行时间不会明显减少。此外,由图4(b)可知,算法的分类准确度会随着节点数目的增加而逐渐减小,从2个节点增加到16个节点,算法的分类准确度从96.3%降低到90.2%。随着数据的不断划分,数据的空间分布会发生改变,根据GDC策略得到的支持向量会发生变化,导致算法的分类准确度降低,因此在提高算法执行效率的同时应该考虑节点数目增加导致算法分类准确度降低的问题。综合上述分析,GIESVM-MR算法处理大数据环境下的分类问题具有更强的适应性以及更好的分类准确度。 为解决并行SVM算法在大数据背景下存在噪声数据较敏感,训练样本数据冗余等问题,提出了基于粒度和信息熵的GIESVM-MR算法。首先,该算法对原始数据集提出了噪声清除策略NC对每个特征属性的重要程度进行评价,获得样本与类别之间的相关度,有效的识别和删除大数据环境下的噪声数据;其次提出基于粒度的数据压缩策略GDC, 通过筛选信息粒的方式保留类边界样本删除非支持向量,获得规模较小的数据集,从而解决了大数据环境下训练样本数据冗余问题;最后结合Bagging的思想和MapReduce计算模型并行化训练SVM,生成最终的分类模型。为了验证GIESVM-MR算法的性能,在NDC、Skin-Segmentain和Cover type 3个数据集下与现有算法进行综合性能对比分析。实验结果表明GIESVM-MR算法的分类效果更佳,且在大规模的数据集下算法的执行效率更高。2.2 数据压缩
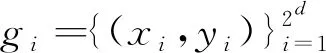
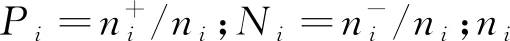
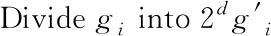
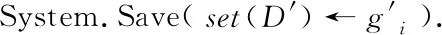
2.3 并行SVM模型构建
2.4 GIESVM-MR算法步骤
2.5 GIESVM-MR算法的时间复杂度分析
3 实验结果及分析
3.1 实验环境
3.2 实验数据

3.3 评价指标
3.4 参数选取

3.5 算法性能比较分析
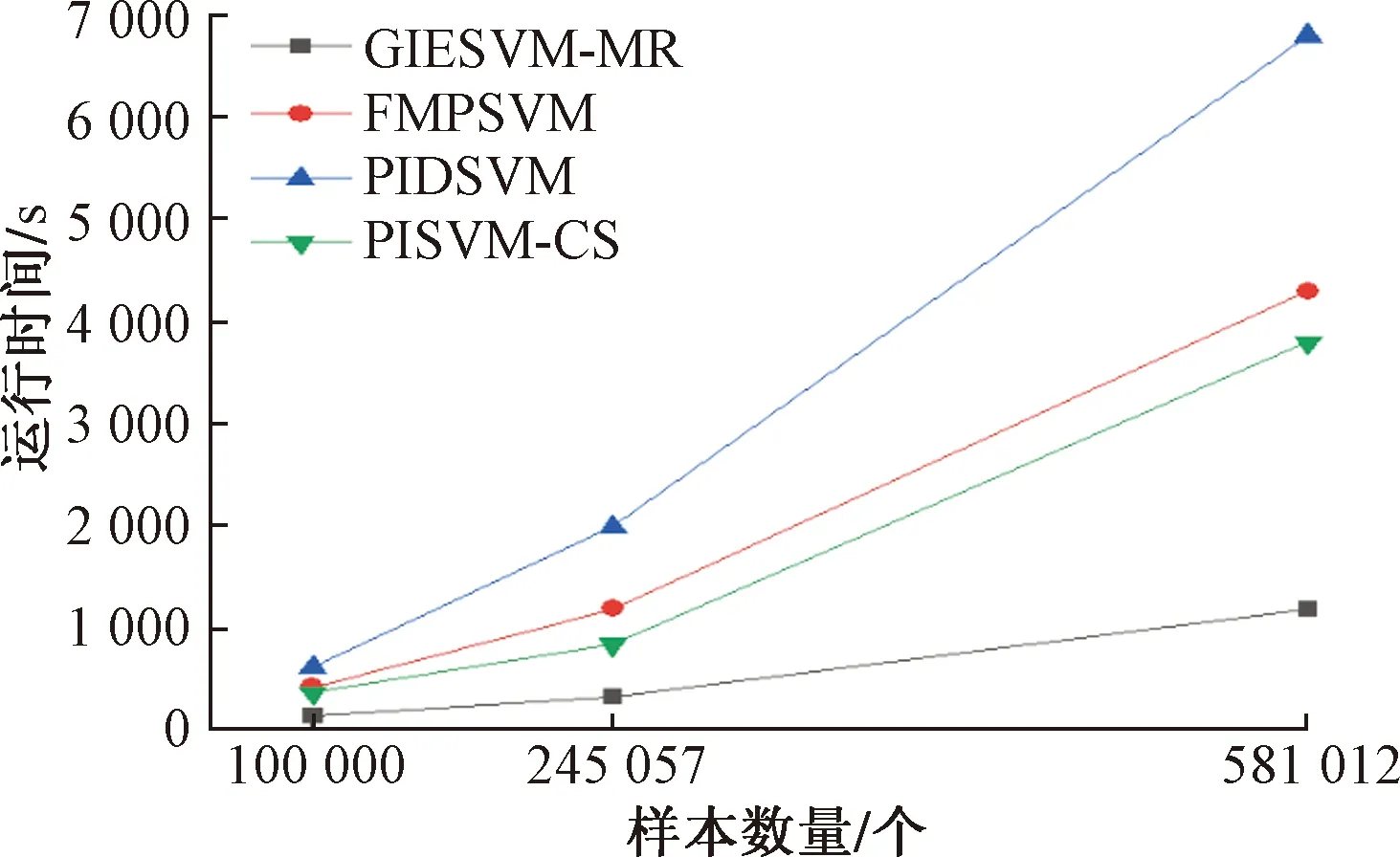
3.6 算法的可扩展性分析
4 结论
