水下大臂展机械手动力学建模与仿真分析
2021-05-14张奇峰张运修孙英哲范云龙
刘 涛, 张奇峰, 张运修, 孙英哲, 范云龙
(1.中国科学院沈阳自动化研究所机器人学国家重点实验室,辽宁沈阳 110016;2.中国科学院机器人与智能制造创新研究院,辽宁沈阳 110169;3. 辽宁省水下机器人重点实验室,辽宁沈阳 110169; 4.中国科学院大学,北京 100049)
引言
水下机械手是作业型水下机器人的核心工具,其性能决定了水下机器人的作业能力,随着海洋资源的开发利用及其关键技术的日趋成熟,水下机械手得到了越来越广泛的应用。水下机械手按驱动方式分为液压机械手[1]和电动机械手[2]。水下液压机械手发展比较成熟,有较强的负载能力,但需要复杂的液压系统支持[3];水下电动机械手体积小,重量轻,控制精度较高,可通过关节内部充油进行压力补偿以适应深海作业[4]。当前水下机械手的研究主要集中在0.5~2 m 之间的臂展[5],搭载在中小型遥控水下机器人及载人潜水器上,开展深海布放、拾取、采样及辅助测量等作业,大范围的移动依赖机器人本体的移动。随着深海作业愈加复杂和专业化,大臂展机械手在一些作业领域显现出明显的优势,如深海实验站等大型装备的原位作业,保持实验站静止而动作较大臂展的机械手,可以更好地保持环境参数,覆盖更大作业范围及获得更高的重复作业精度;同时,对于水下大型装备的捕获,也需要更大臂展及作业范围的机械手。
大臂展机械手在空间领域发展较早。加拿大航天局开发的SSRMS最大臂展约17 m,重达1.63 t,可进行国际空间站硬件的装配、维修和更换[6];美国宇航局中性浮力实验室开发的Robonaut大臂展机械手用于配合航天员模拟失重训练,需将最大线速度控制在 0.3~0.6 m/s 之间,以减小水动力影响[7]。当前,小臂展的水下机械手驱动设计较为保守,关节驱动力矩设计余量较大;受制于电机、减速机及制动器等元器件的约束,水下大臂展机械手的设计需要较为精确地评估关节驱动力矩,因此动力学建模和关节驱动力的求解是设计阶段迫切需要解决的问题,也是本研究的重点。
1 运动学分析
6R串联型机械手具有工作空间/占地比大、结构紧凑、灵活度高等优点[8],在许多领域应用广泛。本研究所述的水下大臂展机械手采用R1⊥R2∥R3∥R4⊥R5⊥R6构型,如图1所示。相比常规臂展水下机械手,大臂展机械手的第2,3关节连杆加长以增大作业空间,末端连杆不变以兼具灵巧性。由于关节2,3连杆较长,前3个关节所需驱动力矩较大,是重点研究对象。
1.1 正运动学分析
机械手运动学方程,是建立每2个相邻连杆之间的坐标变换关系,与世界坐标系或基坐标系联系起来,表示末端位置和姿态的方程。连杆i-1与连杆i之间坐标系变换为旋转变换和平移变换的叠加,即[9]:
Rot(xi,αi-1)
(1)
式中,ai-1—— 连杆长度
αi-1—— 连杆扭转角
θi—— 关节夹角
di—— 连杆偏距
利用D-H法[10]建立图1所示构型6R水下大臂展机械手的坐标系,连杆示意图如图2所示,连杆参数表如表1所示。

图1 水下大臂展机械手构型

图2 水下大臂展机械手连杆示意图

表1 水下大臂展机械手D-H连杆参数表


(2)
其中,位置矢量P=(pxpypz)T表示末端连杆位置;旋转矩阵R=[noa]代表末端连杆的方位。已知各关节角θ1,θ2,θ3,θ4,θ5,θ6,可以求解得到末端位置和姿态。
1.2 逆运动学分析
逆运动学是机械手运动控制的基础,为使机械手末端到达目标位置和姿态,必须求得相应的各关节转角θi。水下大臂展机械手的末端3个关节轴线相交于一点,所以有封闭解,利用几何法与欧拉角法求得机械手的逆解。
利用三角代换:
(3)

逆解出各关节角度分别为:
(4)
2 动力学分析
水下大臂展机械手机械结构外形如图3所示,其中关节2,3连杆长度分别为L1,L2。末端的3个连杆相对整机尺寸较小、质量较轻(水下配成中性浮力),其运动对机械手整机影响相对较小,故在分析水下大臂展机械手的动力学时,为简化计算,将末端3个关节和负载视为1个刚体,重点研究前3个关节驱动力矩。

图3 水下大臂展机械手机械结构及坐标转换
对水下大臂展机械手进行受力分析,可得其动力学模型的一般表达式[12]:
(5)
式中,τ—— 关节驱动力矩,τ=[τ1τ2τ3]T

M—— 包括质量的惯量矩阵

C—— 离心力系数和科氏力系数
H—— 浮力和重力项,为常数
JT—— 力雅克比矩阵,是速度雅克比矩阵J的转置
FF—— 末端受到的力
DL—— 水动力项
2.1 连杆运动的传递
为了方便水动力项求解和末端线速度控制,需要求解各关节的的角速度、角加速度以及各连杆的线速度、线加速度。
连杆i+1的角速度相对于自身坐标系∑i+1的表达式为[13]:
(6)

坐标系∑i+1原点的线速度在坐标系∑i+1中的表达:
(7)
式中,iPi+1为坐标系∑i+1在坐标系∑i的位置向量。按照图3所示坐标系,可得前3个关节的线速度。

(8)
式中,J为速度雅克比矩阵。
对式(6)求导,可得连杆i+1的角加速度相对于坐标系∑i+1的表达式:
(9)
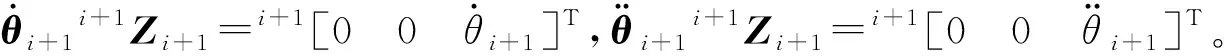
对式(7)求导,并考虑连杆质心的位置矢量iPci,可得各连杆质心处的线加速度在连杆坐标系下的表达:
2.2 水动力项求解
水下大臂展机械手所受的水动力主要来自流体环境影响和关节旋转。各连杆上不同位置的速度、加速度可由2.1节求解,本节将使用莫里森公式和D-H理论求解动力学模型中的水动力项。
莫里森方程将水流对物体的水动力分为两部分:一部分为同相对速度的平方以及投影面积成正比的拖曳力项,另一部分为同相对加速度以及单位体积成正比的惯性力项[12]。
物体受到的拖曳力为:
(11)
式中,CD—— 拖曳力系数,与物体形状有关
ρ—— 海水密度
A—— 垂直于速度方向投影面积
μx—— 水平速度,通过μx|μx|决定拖曳力的正负
物体受到的惯性力为:
(12)
式中,CM—— 惯性力系数,与物体形状有关
V0—— 单位物体排水体积
将由式(11)和式(12)推导水下机械手的水动力项。连杆受水动力如图4所示,其中difDK为杆上微元k受到的水动力,dl为微元长度,iνDK为水流与杆的相对速度,iνSDK为水流与杆在垂直与杆方向上的相对速度,PK为微元在杆坐标系下的位置向量,jrk为微元k相对于坐标系j的位置向量,jri为i坐标系相对于j坐标系的位置向量,irk为微元k相对于i坐标系的位置向量。

图4 水下机械手连杆所受的水动力
水流在根关节坐标系下的速度为:
0νw=[νwxνwyνwz]T
(13)
则其在各关节坐标系下的速度为:

(14)
杆上微元k在各关节坐标系下的速度为iνki,其在各坐标系下的位置向量为Pk=[lk0 0]T,则其在关节坐标系下的速度用如下公式计算:
iνk=iνi+ωi×iPk
(15)
则水流与微元的相对速度为:
iνDk=iνw-iνk
(16)
根据参考文献[14],沿杆的切向的水动力很小,故利用垂直于杆方向的速度计算拖曳力。

iνSDk=SyziνDk
(17)
则圆柱杆微元上的拖曳力为:
(18)
其中“∘ ”为哈达玛积(Hadamard product),表示矩阵对应项相乘。
式中,Ri—— 圆柱杆的半径,m
2Ridl—— 微元在垂直于杆速度方向的投影面积,m2
则微元上的拖曳力对坐标系j的力矩为:
(19)
jrk可由i坐标系相对于j坐标系的位置向量jri和微元k相对于i坐标系的位置向量irk代替,于是上式变成:
(20)
上式为i杆上的微元对坐标系j的拖曳力矩,对上式求积分得到i杆受到的拖曳力对坐标系j的拖曳力矩:
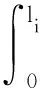
(21)
对上式求和可得到所有杆上受到的拖曳力对坐标系j产生的力矩:
(22)
对上式右乘关节z向的方向向量jzj=[0 0 1]T,可得关节j上水动力产生的关节力矩:
(23)
同理,对式(19)进行修改可得圆柱杆微元上的惯性力:
(24)
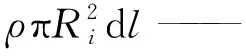

对上式按照式(19)~式(23)的方法进行推导,可得惯性力产生的关节力矩计算公式:
(25)
则关节所受水动力矩τd为:
τd=DL=[τd1τd2τd3]T
=[τD1+τA1τD2+τA2τD3+τA3]T
(26)
2.3 其他力项求解
通过拉格朗日公式推导可得出惯性力、离心力、科氏力的合力矩[9]:
(27)
末端3个连杆以及负载对关节产生的力矩为:
τs=JTFF=[τs1τs2τs3]T
(28)
式中,FF=[FxFyFzτxτyτz]T为末端的负载,JT为力雅克比矩阵,是速度雅克比矩阵J的转置,矩阵J可用式(8)求解。
则动力学模型表达式(5)可改写为:
τ=τk+τs+τd
(29)

3 仿真分析
以上章节构建了水下大臂展机械手的运动学和动力学模型,并求解了关节驱动力矩τ的函数表达式。本章将结合具体运动实例进行分析,水下大臂展机械手机械结构如图5所示,相比正常机械手,其连杆2,3较长、前3个关节负载较大。由于水下大臂展机械手的重量尺寸大,负浮力会产生较大静力矩,故通过使用臂杆配浮力材的方式使其整体在水下呈中性浮力(即H=0)。该手搭载于最高航行速度为2.5 kn的大型载体上,其极限作业目标为:将负浮力为10 kg的小体积重物放入采样篮中;辅助长5.02 m,直径543 mm,质量为400 kg的中性浮力的大型自治水下机器人(AUV)回坞,各连杆详细参数见表2。

图5 水下大臂展机械手三维模型
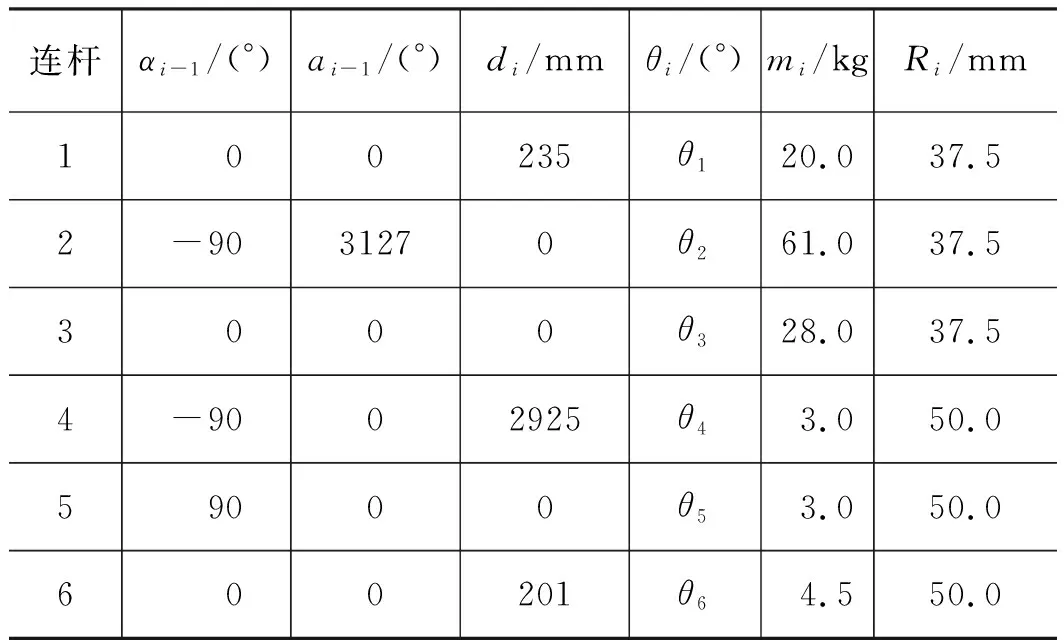
表2 水下大臂展机械手D-H连杆参数表
工业机器人的动力学模型已经比较成熟,故惯性力、离心力、科氏力项不再重复验证。将单个臂杆简化为长3 m、外径100 mm的圆柱体,使用Computational Fluid Dynamics(计算流体动力学)软件进行水动力数值仿真,令臂杆绕其关节(垂直于臂杆轴线方向)以角速度ω旋转,仿真得出关节所受水动力矩。如图6所示,对10组不同角速度下的关节水动力矩仿真值进行二阶的最小二乘法拟合,结合式(21)可解其拖曳力系数CD值[15]。

图6 不同角速度下关节水动力矩
分别假设末端空载、夹持重物或AUV以及载体是否移动的场景,分析水下大臂展机械手末端靠近目标点过程中各关节所受的各部分力矩。在该过程中,机械手末端以夹爪朝下的固定姿态从世界坐标系∑0的坐标点(807,-4580,667)运动至点(-69,-485,1826)。在始末位置之间采用五次多项式插值法进行机械手轨迹规划以完成上述动作,该过程中各关节角速度ω和角加速度ψ见图7。
根据式(26)可求解出该过程中各关节所受水动力矩,各关节所受水动力矩大小与连杆形状、迎流面积、排水体积均有关系。在静水中末端靠近目标点时各关节所受水动力矩如图8a所示,结合图7a可知,水动力矩与关节角速度平方成正比。当载体全速前进时,水下大臂展机械手在0νw=[0 -0.514 0]Tm/s的水流环境中完成该动作,各关节所受水动力矩如图8b所示。加载沿世界坐标系y轴方向的水流前后,关节1,2,3所受最大水动力矩分别增加了0,216,120 N·m。通过轨迹规划可减小运动过程中臂杆的迎流面积,从而减小水流引起的关节水动力矩。
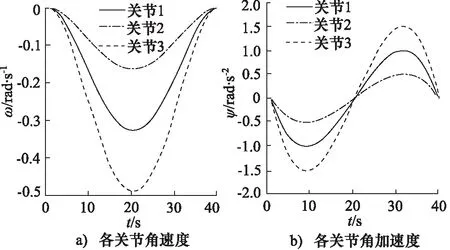
图7 靠近目标点过程中各关节角度信息
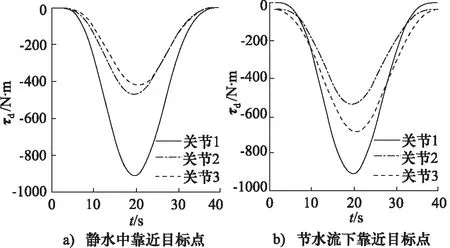
图8 靠近目标点过程中各关节所受水动力矩
根据式(27)可求解出末端靠近目标点过程中前三关节所受的惯性力、离心力、科氏力的合力矩,该力矩与各连杆质量、关节角速度及角加速度均有关。空载状态时末端靠近目标点的过程中各关节力矩如图9a所示,结合图7b可知,该力矩的大小与对应关节的角加速度成反比,会阻碍关节的加速运动。当该手夹持质量为400 kg 的AUV完成相同动作时,由于AUV对惯性张量的影响,各关节力矩如图9b所示,相对图9a空载状态成比例的增大。故在运动轨迹规划时,需要考虑末端负载的质量,以设定机械手各关节相应的角加速度上限。另外,在满足刚度条件下,选用轻质的复合材料臂杆替换合金材料臂杆,可大幅度减小运动过程中各关节所受的合力矩。

图9 靠近目标点过程中惯性力、离心力、科氏力的合力矩
根据式(28)可求解出靠近目标点过程各关节所受的末端力矩。空载靠近目标点过程中,3个关节所受末端作用力矩均为0。当该手夹持负浮力为10 kg的重物以相同动作放回采样篮中时,末端负载为FF=[0 0 -100 N 0 0 0]T,该过程各关节所受末端作用力矩如图10a所示。

图10 靠近目标点过程中各关节所受末端作用力矩
当载体全速前进、机械手夹持大型AUV以相同动作完成回收时,AUV的运动可分解为随载体0.514 m/s前向运动和随机械手向下的1 m/s的侧向运动。将AUV三维模型进行简化,并通过水动力仿真分别求2个方向的水动力,图11a和图11b分别为AUV前向和侧向运动时所受的压力云图,得出末端力为FF=[0 401.5 N 747.1 N 0 0 0]T,该过程各关节所受末端作用力矩如图10b所示。故在运动轨迹规划时,需要考虑末端负载的净浮力和水动力,以设定机械手各关节相应的角速度上限。

图11 AUV移动过程水动力仿真压力云图
根据式(29)的动力学模型,可求解出水下大臂展机械手动作过程中各关节所需的驱动力矩。在设计水下大臂展机械手时,需根据应用需求(包括作业空间、环境水流速度、负载),并在其所有工作位置和姿态内选取关节所受力矩的最大值,作为极端情况设计关节驱动模块、校核臂杆强度。在分析水下大臂展机械手时,可对负载能力、响应速度进行估算。
4 结论

