如何正确运用χ2检验<br/>——病例对照设计四格表资料的χ2检验

如何正确运用χ2检验
——病例对照设计四格表资料的χ2检验

2021-05-14胡纯严胡良平

四川精神卫生 2021年2期

胡纯严，胡良平，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在流行病学研究或临床研究中，为了较快地找到可能导致某种疾病发生的原因，研究者需要开展“病例对照研究”。也就是找到与病例组条件接近的对照组，基于临床专业知识，提出各种可能导致所研究疾病发生的全部可疑因素，回顾性调查病例组与对照组受试对象接触各种可疑因素的情况，计算并比较两组受试对象接触各种可疑因素的比例，从而为确定导致所研究疾病发生的可能危险因素提供线索。

若假定每个可疑危险因素只分为“接触”与“未接触”两个水平，此时，基于病例对照设计所收集的资料就可以简化成“病例对照设计四格表资料（参见下文表1和表2）”。对其进行统计分析主要包括两个方面：其一，检验“患病与否”与“接触与否”之间是否存在关联性（所需要的统计分析方法与处理横断面设计四格表资料的统计分析方法相同，参见文献［1］）；其二，检验“优势比（Odds ratio，OR）是否等于1”。本文着重介绍优势比的概念、对总体OR的Mantel-Haenszel’s χ2检验（简称 MH χ2检验）、对总体OR的区间估计方法以及使用SAS和R软件实现计算的方法。

1 病例对照设计的概念及其四格表资料的实例

1.1 概念

所谓“病例对照设计”，就是依据专业知识和基本常识，提出一些“重要的非试验因素（如年龄、性别、职业、生活环境、生活方式等）”，针对现有“病例组”具备的条件，寻找在前述重要的非试验因素方面与“病例组”非常接近但未患所研究疾病的另一组人群，他们被称为“对照组”；再依据专业知识，提出一些可能导致所研究疾病发生的“可疑影响因素”，让前述提及的两组受试对象回忆之前是否接触过这些“可疑影响因素”。于是，计算出两组人群对每种“可疑影响因素”的“接触比例”，进而依据统计学原理对其进行假设检验。

1.2 病例对照设计四格表资料的表达模式

从前面的“概念”可知，在病例对照设计资料的收集过程中，先有“患病”与“未患病”的结果分档，后有“接触危险因素（简称‘接触’）”与“未接触危险因素（简称‘未接触’）”的原因分组，故其四格表资料的表达模式见表1。

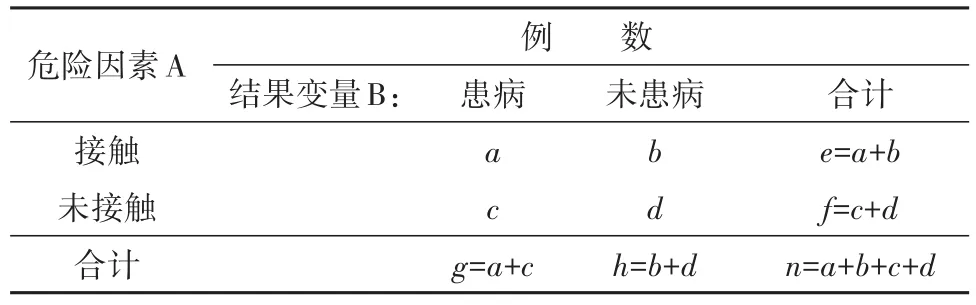
表1 n个受试对象病例对照研究结果的表达模式

1.3 实例

【例1】在文献［2］中，作者根据MINI 5.0中文版自杀模块判断未治疗抑郁障碍患者有无自杀风险，共6个条目，评分范围0～33分。评分＜6分为无自杀风险，评分≥6分为有自杀风险。假定作者收集资料时，首先关注的是“是否伴有精神病性症状”，并将其视为“结果变量”。在此基础上，对“有精神病性症状”与“无精神病性症状”的两组受试对象进行回顾性调查或测量，从而获得两组受试对象中各自“有自杀风险者所占的比例”，具体数据见表2。

表2 未治疗抑郁障碍患者“有无精神病性症状”与“有无自杀风险”之间关系的调查结果

对表2资料进行统计分析涉及以下两个问题：①“有无精神病性症状”与“有无自杀风险”之间是否存在独立性；②“有精神病性症状”与“无精神病性症状”的优势比是否等于1。

【统计分析方法的选择】回答第1个问题，可选用“Pearson’sχ2检验”或“校正的 Pearson’sχ2检验”或“似然比χ2检验”或“Fisher’s精确检验”。因为这些检验方法所对应的零假设均为“两属性变量互相独立”；回答第2个问题，需要先计算“OR”，然后选用“Mantel-Haenszel’sχ2检验”，该检验的检验假设为：“H0：OR=1，H1：OR≠1”。因为 MHχ2检验所对应的零假设为“优势比等于1”。

1.4 独立性检验方法

虽然病例对照设计四格表资料中的两个变量有“原因变量”与“结果变量”之分，但在回答两变量之间是否存在“独立性”时，仍可将其视为“两属性变量”之间关系的研究问题，故可采用的统计分析方法与横断面设计四格表资料是完全相同的，具体方法参见文献［1］。因篇幅所限，此处不再赘述。

2 优势比的概念、假设检验与区间估计

2.1 概念

OR是两个人群odd值之比值［3-4］，这两个人群分别受到一个可疑危险因素两个水平（例如接触与未接触）的影响。具体地说，OR是病例组的“odd病例”与对照组的“odd对照”之比，它揭示了“危险因素的两个水平”在两组中的相对作用强度大小。若OR＞1，表明“危险因素”对“病例组”的影响大于对“对照组”的影响；反之亦然。OR的计算公式如下：

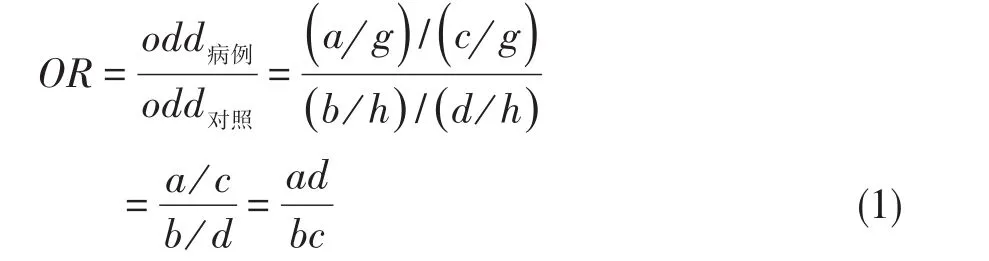
前提条件：两个人群应处于相同的地理环境之中，生活在相同的时间区间内；每个人群都有足够大的样本含量（两个人群的样本含量之差越小越好）；对照组在一切重要的非试验因素方面与病例组越接近越好；应避免带有诱导性的提问；应尽可能保证在回顾性调查过程中，每位受试对象通过回忆给出的回答越准确越好。

2.2 假设检验

OR是一个一般的样本统计量，存在抽样误差，要想知道总体中的OR是否为1，就需要对其进行假设检验，即

对式（2）进行假设检验所需要的检验统计量为Mantel-Haenszel’s χ2，一般记为χ2MH，见下式：

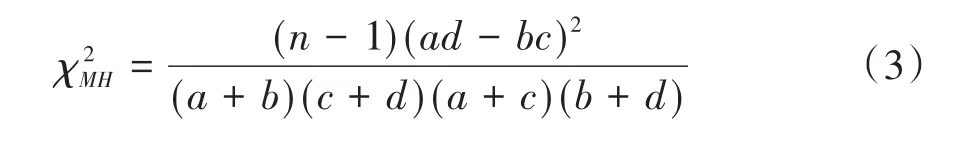
2.3 区间估计

2.3.1 概述

由于OR是一个一般的样本统计量，通常，人们需要知道与其对应的总体参数所在的范围，这就是总体优势比的区间估计问题。在SAS/STAT的FREQ过程中［5］，给出了三种置信区间的计算方法，即“渐近置信区间法（简称WALD法）”“评分置信区间法”和“精确置信区间法”［4-5］。

2.3.2 渐近置信区间法

OR的渐近100（1-α）%置信区间的计算公式：

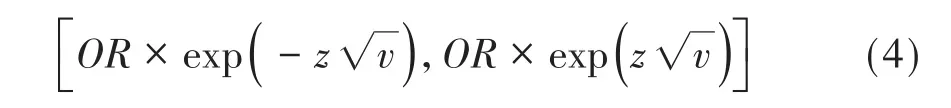
在式（4）中，z是标准正态分布曲线下左侧面积为100（1-α/2）%处横坐标轴上的分位数；而v为对数优势比的方差，见下式：

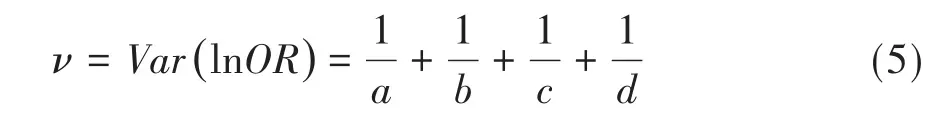
2.3.3 评分置信区间法

满足式（7）的所有θ值构成OR的100（1-α）%置信区间。

2.3.4 精确置信区间法

基于Thomas和Gart提出的方法［5］，用迭代的方法求解下列两个方程，可以获得置信限的下限和上限值φ1和φ2：

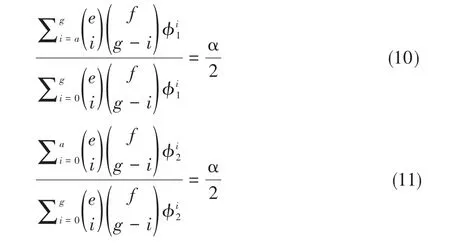
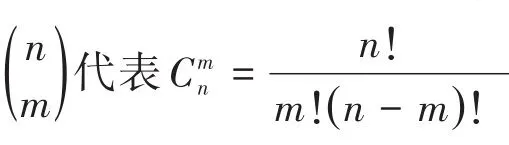
3 病例对照设计四格表资料统计分析的软件实现

3.1 问题与数据

【例2】沿用例1中的“问题与数据”，试完成下列4项任务：①检验两变量（即“有无精神病性症状”与“有无自杀风险”）之间的关联性；②计算优势比（OR）；③对OR进行假设检验，即“H0：OR=1，H1：OR≠1”；④对OR进行区间估计。

3.2 基于SAS实现独立性检验、计算OR值及求其置信区间

所需要的SAS程序如下［5-6］：

【程序说明】第一个过程步对四格表资料进行“关联性或独立性”检验（包括检验、校正检验、检验和Fisher’s精确检验）；计算OR值，还包括对OR是否等于1的检验。第二个过程步对四格表资料进行“OR值计算”，并基于“渐近置信区间法（即WALD法）”求“OR值的95%置信区间”。第三个过程步对四格表资料进行“OR值计算”，并基于“评分法”求“OR值的95%置信区间”。第四个过程步对四格表资料进行“OR值计算”，并基于“精确置信区间法（简称精确法）”求“OR值的95%置信区间”。

【SAS主要输出结果及解释】

第一部分，“关联性或独立性”检验结果见表3。

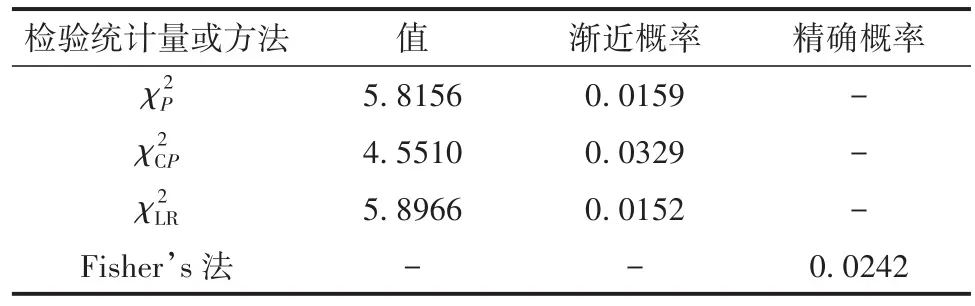
表3 例1中病例对照设计四格表资料关联性或独立性检验结果

第二部分，优势比的计算结果及其假设检验的结果：OR=4.0915，=5.7659，渐近概率=0.0163。

第三部分，基于三种方法估计总体优势比OR值的95%置信区间的结果如下。渐近法：［1.2190，13.7329］；评分法：［1.2704，13.0550］；精确法：［1.1022，18.6182］。

【结论】由表3结果可知，“有无精神病性症状”与“有无自杀风险”之间是不独立的，具体地说，“有精神病性症状”者比“无精神病性症状”者具有更大的“自杀风险”，其OR=4.0915；总体中OR值的95%置信区间随着计算方法的改变略有变化，即渐近法：［1.2190，13.7329］；评分法：［1.2704，13.0550］；精确法：［1.1022，18.6182］。

3.3 基于R实现独立性检验以及OR值的计算、假设检验与区间估计

所需要的R程序如下［6-7］：

【程序说明】“＞”代表R软件运行环境中的“提示符”，上面的R程序中共有3个提示符，说明共有3个R语句；第一句将四格表资料组织成一个矩阵；第二句调用函数fisher.test（），此函数将采用Fisher’s精确检验实现四格表资料的“独立性检验”，同时，还计算优势比OR的值，并采用精确法求总体OR值的95%置信区间；第三句调用函数chisq.test（），此函数将采用校正公式进行Pearson’sχ2检验（即实现两属性变量之间的独立性检验）。

【R主要输出结果及解释】

以上结果表明，采用Fisher’s精确检验对四格表资料中两属性变量进行独立性检验得到的结果为：P=0.02423，优势比OR=4.042456（注意：与前面基于SAS计算得出的OR=4.0915略有出入），基于精确法求得总体OR的95%置信区间为［1.1022，18.6130］。

以上为进行了连续性校正的Pearson’s χ2检验结果，即=4.551，P=0.0329。

【结论】参见前文SAS输出结果及结论，此处从略。

4 讨论与小结

4.1 讨论

在SAS/STAT的FREQ过程中［5］，增加了一些新的方法求总体优势比OR值的置信区间，其中，精确置信限的计算方法计算得出的下限值与其他两种方法计算的下限值比较接近，而上限值比其他两种方法计算得出的上限值大得多，其原因有待进一步查证。

“病例对照研究”是一种“由果溯因”的研究，它只能为探索疾病的“因果关系”提供线索，而不能提供确凿的证据。原因主要有以下几点：其一，很难保证两组人群具有高度的可比性；其二，很难确定每位受试对象接触可疑影响因素的强度（包括作用时间长短和作用量的大小）；其三，很难保证每位受试对象回忆结果的准确性；其四，很难保证真正的危险因素全部都被研究者提出来并加以研究。

在实际科研工作中，无论基于队列研究设计还是病例对照研究设计收集的资料通常都是多因素多结局的资料，一般来说，常将多结局变量分解成一个一个的结局变量，但应该将多个原因变量同时纳入统计分析（即选用多重回归分析或其他多因素统计分析），这样不仅可以克服单因素分析的许多弊端，还有利于考察因素之间的交互作用是否对结果变量具有不可忽视的影响，使所获得的结果和结论更可靠。