如何正确运用χ2检验——两种单向有序二维列联表资料线性趋势χ2检验

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

对于列联表资料而言，最常见的统计分析目的是“独立性检验（其本质仍属于差异性检验）”。但针对某些特殊的列联表资料，其分析目的也可以是“相关分析（例如，可用Kendall’s Tau-b秩相关分析处理配对设计扩大形式的二维列联表资料；可用Spearman’s秩相关分析处理双向有序二维列联表资料）”，还可以是“线性趋势检验”（例如，可分别用Cochran-Armitage’s线性趋势检验和Lee’s线性趋势检验处理单向有序二维列联表资料）。本文将介绍两种单向有序二维列联表资料及其线性趋势检验的原理和软件实现的方法。

1 两种单向有序二维列联表资料的实例与统计分析方法选择

1.1 单向有序R×2表资料的实例

【例1】文献［1］中有一个单向有序的R×2表资料，见表1。

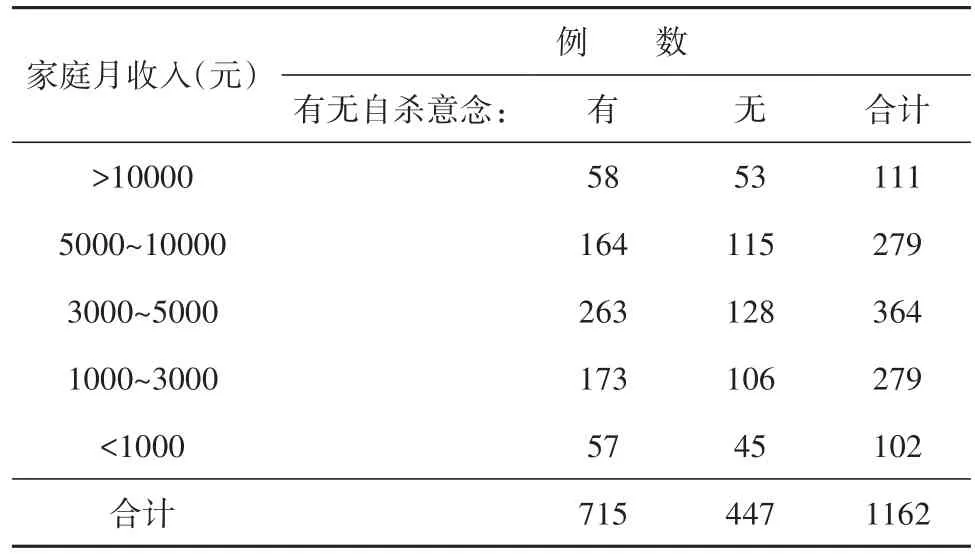
表1 家庭月收入（元）与有无自杀意念之间关系的调查结果

1.2 单向有序2×C表资料的实例

【例2】文献［2］中有一个单向有序的2×C表资料，见表2。

表2 治疗4周末两组临床疗效观测结果

1.3 统计分析的目的与统计分析方法的选择

1.3.1 以表1资料为分析对象

若分析目的是考察“家庭月收入”与“有无自杀意念”之间是否独立，需要选择χ2检验或Fisher’s精确检验；若分析目的是比较5种家庭月收入的受试对象“有自杀意念的发生率”之间的差异是否具有统计学意义，仍需要选择χ2检验或Fisher’s精确检验；若分析目的是考察“有自杀意念的发生率”是否随着“家庭月收入的减少”而呈线性递增或递减趋势，则需选择Cochran-Armitage’s线性趋势χ2检验。

【说明】对于表1资料而言，上面描述的前两个分析目的在本质上是完全相同的，故可选用的统计分析方法相同。因篇幅所限，本文只进行Cochran-Armitage’s线性趋势χ2检验。

1.3.2 以表2资料为分析对象

若分析目的是考察“组别”与“疗效”之间是否独立，需要选择χ2检验或Fisher’s精确检验；若分析目的是比较两组疗效之间的差异是否有统计学意义，需要选择秩和检验；若分析目的是考察研究组在四种“疗效”等级上的“相对比例”从“痊愈”到“无效”是否呈线性递减或递增趋势，需要选择Lee’s线性趋势χ2检验。

【说明】因篇幅所限，本文只进行Lee’s线性趋势χ2检验。

2 单向有序R×2表资料的线性趋势检验

2.1 单向有序R×2表资料的表达模式

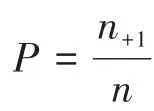
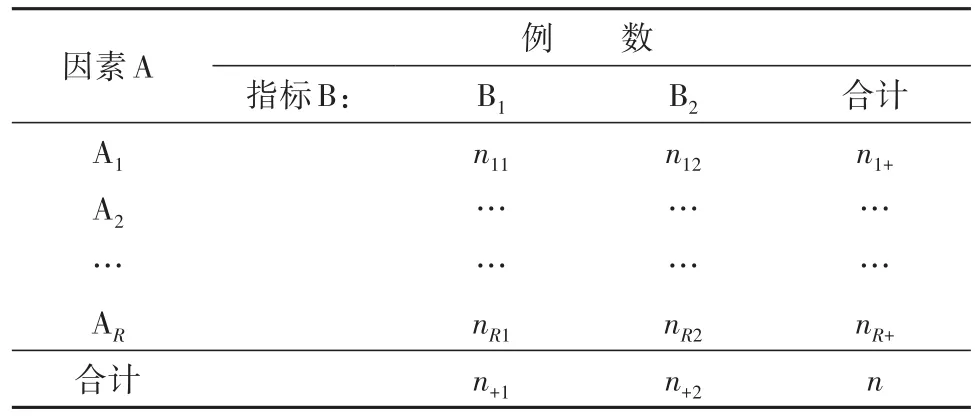
表3 R×2列联表资料的表达模式

2.2 检验方法概述

2.2.1 检验假设

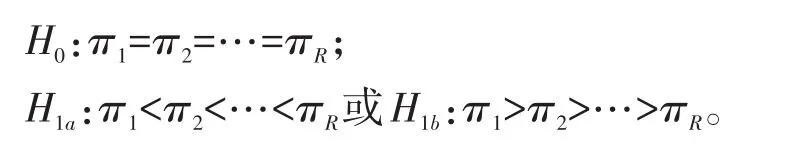
设置显著性水平为：α=0.05。

2.2.2 检验统计量

Cochran-Armitage’sχ2检验的检验统计量［3］见下式：

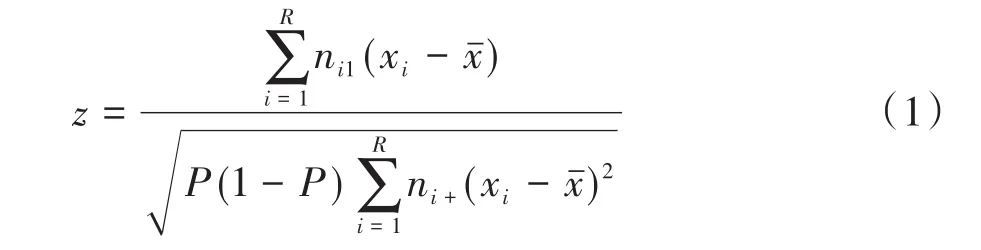
2.3 基于SAS软件实现计算

【例3】沿用例1的资料，试基于SAS软件检验“有自杀意念的发生率”是否随着“家庭月收入的减少”而呈线性递增或递减趋势。

【分析与解答】为了回答所提出的问题，可选用Cochran-Armitage’sχ2检验，设所需要的 SAS 程序如下：

【程序说明】“tables语句”中的选项“trend”要求采用近似方法进行线性趋势检验；而“exact trend；”语句则要求采用精确方法进行线性趋势检验。

【SAS输出结果及解释】

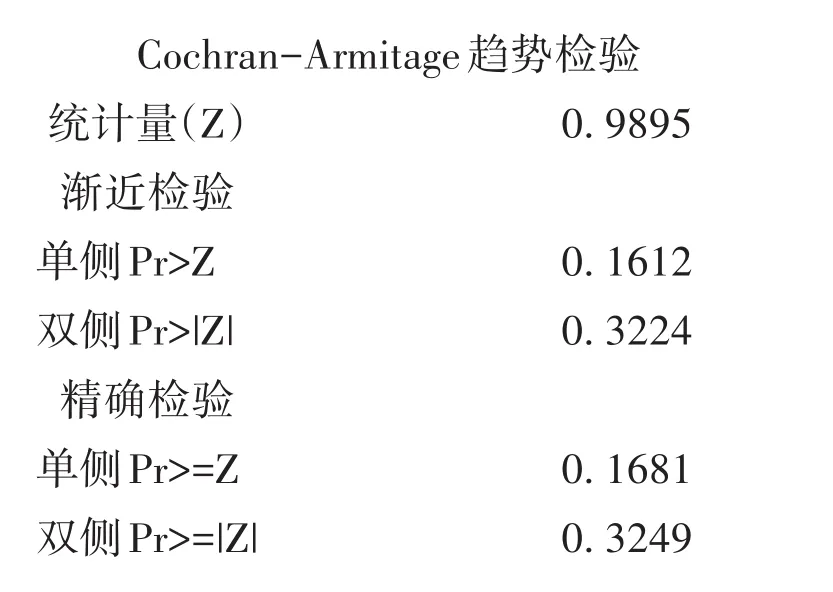
以上结果表明：SAS给出的检验统计量为Z（它服从标准正态分布），但Z的平方就是自由度为1的χ2检验统计量的值；无论采用渐近检验还是精确检验，也无论选用单侧检验还是双侧检验，对应的P值均大于0.05，即“有自杀意念的发生率”不会随着“家庭月收入的减少”而呈线性递增或递减趋势。

2.4 基于R软件实现计算

【例4】沿用例1的资料，试基于R软件检验“有自杀意念的发生率”是否随着“家庭月收入的减少”而呈线性递增或递减趋势。

【分析与解答】为了回答所提出的问题，可选用Cochran-Armitage’sχ2检验，设所需要的R程序如下：

【程序说明】第1行输入表1资料的第1列数据；第2行输入表1资料的纵向合计列数据；实现Cochran-Armitage’sχ2检验的R函数为“prop.trend.test（）”。

以上结果表明：χ2=1.0414，P=0.3075（注意：此计算结果与SAS输出结果略有差别），结论同上（参见第2.3节），此处从略。

3 单向有序2×C表资料的线性趋势检验

3.1 单向有序2×C表资料的表达模式

单向有序2×C表资料的表达模式见表4。

表4 结果变量为有序变量2×C列联表资料的表达模式

3.2 检验方法概述

3.2.1 检验假设

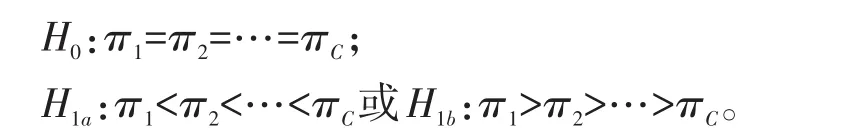
设置显著性水平为：α=0.05。

【说明】πj（j=1，2，…，C）代表第j列上的总体的发生率；H1a代表各列上的“总体率”呈线性递增变化趋势；H1b代表各列上的“总体率”呈线性递减变化趋势。

3.2.2 检验统计量

Lee’s线性趋势检验统计量［5］见下式：

由 χ2分布的定义［4］可知，上式中的“ZLinear”平方为服从自由度为1的χ2分布，即有下式成立：

3.3 基于SAS软件实现计算

【例4】沿用例2的资料，试基于SAS软件检验研究组在四种“疗效”等级上的“相对比例”从“痊愈”到“无效”是否呈线性递减或递增趋势。

【分析与解答】为了回答所提出的问题，可选用Lee’s χ2检验，设所需要的SAS程序如下：

【程序说明】“n=87”代表表2资料中的总频数；“n1=45”代表表2资料中第1行的合计频数；“cards语句”后的3列数据分别是：第1列为4个疗效等级的“分值”；第2列为表2资料中的第1行频数；第3列为表2资料中的横向合计行上的4个频数。

结果表明：Z=-1.565746（χ2=2.452），P=0.058704，说明研究组在四种“疗效”等级上的“相对比例”从“痊愈”到“无效”不呈线性递减或递增趋势。

3.4 基于R软件实现计算

【例5】沿用例2的资料，试基于R软件检验研究组在四种“疗效”等级上的“相对比例”从“痊愈”到“无效”是否呈线性递减或递增趋势。

【分析与解答】为了回答所提出的问题，可选用Lee’s χ2检验，设所需要的R程序［6-7］如下：

【程序说明】以上程序各语句之前都省略了R软件提示符“＞”；第1行为4个疗效等级的“分值”；第2行为表2资料中的第1行频数；第3行为表2资料中的第2行频数。

结果表明：Z=-1.565746（χ2=2.452），P=0.058704，说明研究组在四种“疗效”等级上的“相对比例”从“痊愈”到“无效”不呈线性递减或递增趋势。

4 讨论与小结

4.1 讨论

单向有序R×2表资料的线性趋势检验（简称“前者”）与单向有序2×C表资料的线性趋势检验（简称“后者”）在以下两个方面存在区别。其一，变量的性质及其水平数不同：前者的“原因变量”为“R值有序变量（R＞2）”、“结果变量”为“二值变量”；而后者的“原因变量”为“二值变量”、“结果变量”为“C值有序变量（C＞2）”。其二，构建线性趋势检验统计量的统计学原理不同。前者是利用加权回归分析的思想［8］，将由R×2列联表资料计算得到的总χ2值分解为“线性回归分量A”和“偏离线性回归分量B”两部分。若A有统计学意义、B无统计学意义，说明原因变量与结果变量之间存在线性关系；若A与B都有统计学意义，说明原因变量与结果变量之间可能存在某种非线性关系。而后者是基于多项分布原理进行推导，构造出检验统计量［5，8］，因篇幅所限，此处从略。

尽管SAS软件在给出Cochran-Armitage’s线性趋势检验结果时，呈现了单侧检验和双侧检验两种结果。但由于其备择假设有两种可能情况，而且，在一个实际问题中，只能选择其一（递增趋势或递减趋势），故基于常识可知，线性趋势检验更适合选择“单侧检验”，而不是双侧检验。

值得一提的是：在对以上两种列联表资料进行线性趋势检验时，都涉及到如何给有序变量的各水平进行赋值。一般来说，直接赋值“1、2、3、……”即可；若有专业知识为依据，可给有序变量的各水平赋值为非连续的自然数，例如 1、3、8、15、27、……对于同一个资料不同的赋值方法，所得的计算结果会略有差别，但一般不会明显改变最终的结论。

4.2 小结

本文呈现了两种单向有序二维列联表资料的实例和模式，给出了对其进行线性趋势检验的原理和计算公式；基于SAS和R软件实现了统计计算，对统计软件的输出结果进行了解释，并做出了统计结论和专业结论。