基于STEM教育理念培养高中生科学探究素养
2021-05-14郭晓敏区楚瑜
肖 化 ,郭晓敏 ,曾 辉 ,区楚瑜
1.华南师范大学物理与电信工程学院,广州 510006
2.厦门市槟榔中学,福建 厦门 361000
3.韩山师范学院物理与电子工程学院,广东 潮州521000
1 引言
《普通高中物理课程标准(2017年版)》强调培养高中生未来发展所需的学科核心素养,具体包含物理观念、科学思维、科学探究及科学态度与责任[1]。但目前我国高中物理教学的问题在于受长期分科教育的影响,学生更习惯用学科的思维看待问题,不利于其学习兴趣和综合能力的发展[2]。不仅如此,传统的物理教学注重知识的传授,忽视了培养学生动手探究的能力,从而使其无法深入理解知识的本质及知识在社会生活中的具体应用[3]。STEM是科学 (Science)、技术(Technology)、工 程 (Engineering)、数 学 (Mathematics)的简称,是一种跨学科融合教育,着重培养学生的问题解决能力和工程设计思维。当前,把STEM教育的理念正确融入实际学科教学中,培养学生的动手能力和问题解决能力,已经成为新时代基础教育领域的热点话题[4]。本文尝试将STEM教育融入高中物理教学中,为探索如何培养高中生的科学探究能力提供一条有效途径。
2 构建基于STEM教育的高中物理教学模式
本文将STEM教育与高中物理教学相结合,构建基于STEM教育的高中物理教学模式,力争构建“不仅能让学生全面理解所学习的物理知识,还能让学生在解决问题的过程中体会学有所用”的课堂,强调学生在课堂中的主体地位,培养学生知识迁移的能力和解决问题的创新能力。具体教学模式如图1所示。
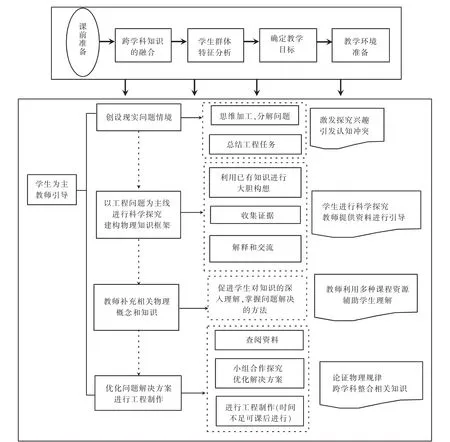
图1 基于STEM教育的高中物理教学模式
本教学模式的教学过程主要有4个环节,每个环节的设计意图、所培养的科学探究素养及STEM教育的依据如表1所示。
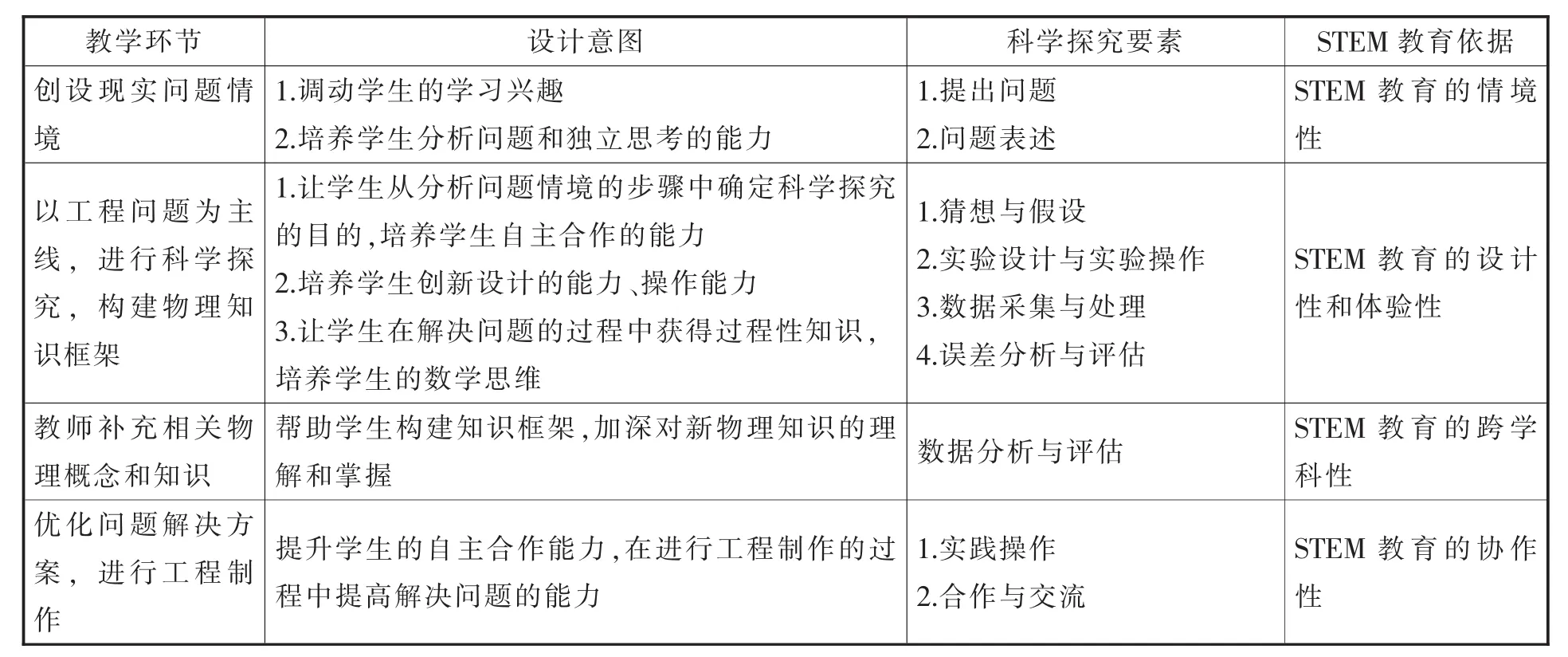
表1 各环节的设计意图及培养的科学探究素养
3 基于STEM教育的高中物理教学实践应用
3.1 教学案例设计
3.1.1 课前准备
《普通高中物理课程标准(2017年版)》对《力的分解》这一节的要求是“通过实验,了解力的分解,知道矢量和标量”[1]。这一节内容通过一个课时完成,上承接重力、弹力、摩擦力三个核心概念,是力的合成的逆运算;下开启共点力的平衡条件等知识,为学习共点力平衡这一重要知识点打下基础,在物理力学体系中占有重要的地位。在本节课中,应创设大量与实际贴合的情境,增加学生的感性认识,以实际情境所呈现的工程任务驱动学生进行科学探究[3],解决问题,最终通过《力的分解》的学习培养学生的科学探究素养和工程思维,进一步提升学生问题解决的能力。
【确定教学目标】
根据课标要求及上述分析,确定本节课教学目标如表2所示。
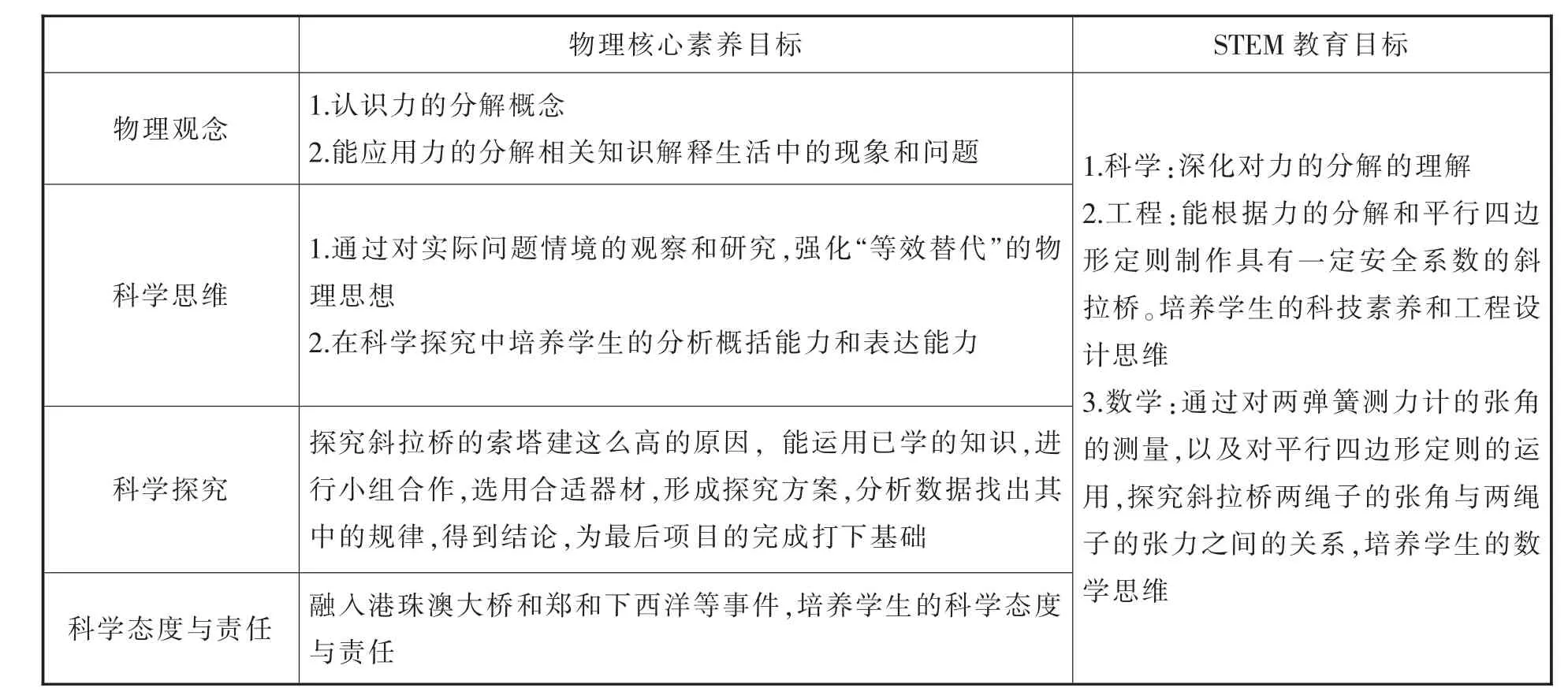
表2 《力的分解》一节的物理核心素养培养目标与STEM教育目标
【教学环境准备】
多媒体、弹簧测力计、刻度尺、硬纸板、铁架台、铅笔、铁丝、细线等。
3.1.2 教学过程
【创设现实问题情境】
用多媒体课件向学生展示港珠澳大桥的有关图片。教师让学生注意观察港珠澳大桥的索塔很高,大约为163米。教师向学生提出问题:“为什么索塔要建这么高?如果让同学们当一回工程师,你在设计这样的跨海大桥的时候将会考虑哪些因素?请大家针对这一问题进行讨论”。教师抛出复杂的问题情境后,引导学生将问题分解成一个个子问题,按照问题的逻辑顺序对问题进行排序,以培养学生分析问题的能力,如表3所示。
fengyukai@vip.qq.com;通信作者,王华森,教授,硕士生导师,博士,主要从事蔬菜生理与分子生物学研究,(电子信箱)whsych66@163.com。
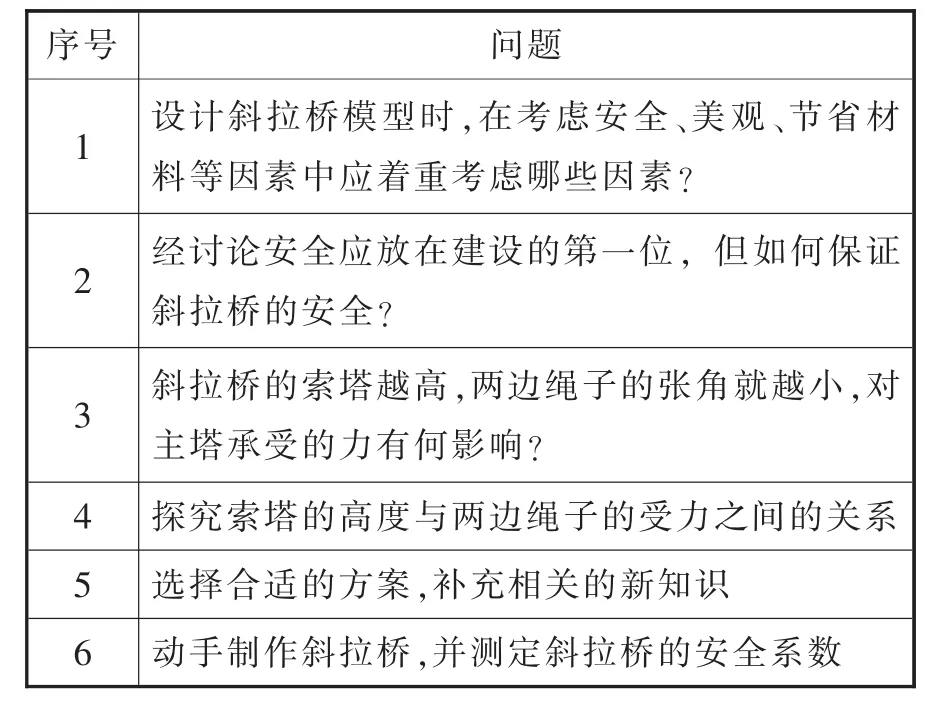
表3 分解后的子问题
STEM设计理念:本环节体现STEM教育的情境性。通过富有挑战性的问题情境能迅速激起学生的探究欲望。一个复杂的问题情境需要对其进行多方面的剖析和分解,突出物理学习的主题,这一过程需要教师一步步的引导。并且,从表3可知,要解决制作斜拉桥模型的工程问题,学生需要学习力的分解这一知识点,在探究中还需运用已学过的平行四边形定则、力的合成、重力等有关知识,实现本章知识的大综合。学生在解决本工程问题的过程中,进行了数学运算,以及技术的使用,实现了STEM教育理念的融入。
培养科学探究素养的设计理念:复杂的问题情境使学生往往不知道从何下手,教师应引导学生将复杂的问题分解成一个个子问题,让学生提出并表述需要探究的物理问题,提升学生提出问题的能力。
【以工程问题为主线,进行科学探究】
(1)提出问题
教师引导:“请同学们观察,索塔高度与斜拉索两边绳子的张角有何关系?现在定义绳子与竖直方向的夹角为θ”。学生们通过观察发现索塔越高,两边绳子的张角越小,于是进一步提出问题:绳子和竖直方向的夹角θ与绳子的张力存在什么关系?
(2)收集证据
引导学生运用力的合成和平行四边形定则的知识画出草图,发现绳子和竖直方向的夹角θ与绳子拉力的大小存在一定关系,猜想:当绳子和竖直方向的夹角θ越大时,两边绳子的拉力越大。
随后,教师引导学生探究绳子和竖直方向的夹角θ与绳子的拉力的关系,验证猜想是否正确。为简化问题,将两根绳子各自与竖直方向的夹角近似看成是相等的。让学生利用桌面上的两个弹簧测力计、钩码进行探究,当改变两个弹簧测力计的夹角时,观察弹簧测力计的示数如何变化,具体装置如图2所示。
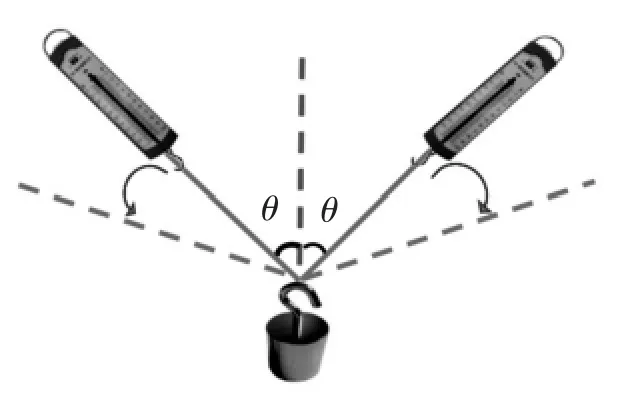
图2 探究绳子和竖直方向的夹角与绳子拉力关系实验装置图
这一过程由学生小组合作完成,并将实验结果记录在提前设计好的表格中,如表4所示。
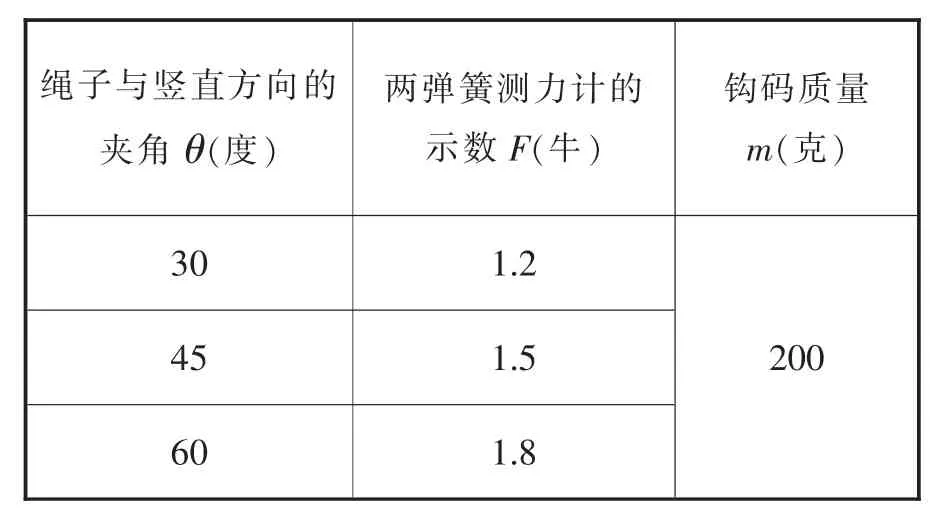
表4 探究绳子和竖直方向的夹角与绳子拉力关系的实验记录表格
(3)解释和交流
学生之间交流实验结果,从实验表格中的数据发现,当钩码的质量不变时,两个斜着的弹簧测力计夹角越大,弹簧测力计示数就越大。引导学生们运用所学知识进行解释,大部分学生能运用力的合成对现象进行解释。将两弹簧测力计的拉力按照其作用效果进行力的合成,其合力方向向上,大小与钩码重力相等,当合力大小和方向不变时,两分力的夹角越大,分力越大,验证之前的猜想。
STEM设计理念:本环节体现STEM教育的设计性和体验性。学生要设计并制作安全系数较高的斜拉桥模型,应先掌握力的分解的科学知识以及斜拉桥的工程设计原理,提升学生科学素养和工程设计素养的同时,以工程任务驱动学生进行科学探究。
培养科学探究素养的设计理念:本环节基于建构知识理论,在学生原有的知识水平上,引导学生提出问题、猜想与假设,提升学生的猜想能力;收集证据,提出解决方案,通过科学探究获得新的物理知识,提升学生实验操作和数据采集的能力,并在交流与合作中获得思维的解放,提升交流与合作的素养。
【教师补充相关物理概念和知识】
教师借助多媒体动画让学生理解若没有条件限制,一个力可以分解成无数多组分力,这就是力的分解,力的分解与力的合成互为逆运算。教师提出问题:“能否对刚刚的实验探究结果用力的分解来解释?如果可以,应该分解哪一个力?为什么要进行力的分解,力的分解的依据是什么?”同时让学生动手作图,体验力的分解。并引导学生解释开始的问题——为什么索塔要建这么高。大多数学生都能将钩码的重力进行分解,但还有少部分学生不知如何下手。因此,教师在教学过程中应启发引导学生思考。
本环节的设计理念:引导学生尝试利用力的分解原理来解释实验结果,培养学生知识迁移的能力。同时,让学生解释为什么重力要沿绳子延长线的方向进行分解,说明利用力的分解将三个力变为了四个力,看似变得复杂了,但是构造出两对平衡力,更体现物理的简洁之美,让学生懂得如何在具体情境中进行力的分解,提升学生的数据分析能力及归纳总结能力。
【优化问题解决方案,进行工程制作】
在学生们已经知道力的分解的定义及为什么要进行力的分解后,引导学生完成新课开始前所布置的工程任务——制作斜拉桥模型,并测试其安全系数。鼓励学生查阅相关资料,参照所提供的器材设计方案,通过理论分析和小组协作,对方案进行优化,确定最终的解决方案。以小组为单位,根据解决方案制作出最终的斜拉桥模型。图3与图4为部分小组的作品。

图3 学生制作的斜拉桥模型(有小车)

图4 学生制作的斜拉桥模型(无小车)
STEM设计理念:本环节体现了STEM教育的协作性。利用数学模型进行理论分析,确定解决方案,利用现代技术手段最终完成工程任务,实现科学(S)·技术(T)·工程(E)·数学(M)的深度融合。
3.2 教学实施效果分析
以某中学高一年级的两个平行班作为实验对象。其中一个班为实验班,应用基于STEM教育的高中物理教学模式;另一个班为对照班,应用传统的高中物理教学模式。由同一位教师对实验班和对照班进行教学,历时一个学期。学期末时对实验班和对照班进行有关科学探究素养的客观测试。将测试成绩分成三类,即科学探究素养的问题、证据、解释要素,对三类成绩进行统计学分析和独立样本T检验。
从表5可以看出,实验班在科学探究素养上问题维度的均值比对照班高了将近0.8分,初步得出实验班学生在提出问题和猜想与假设上的水平比对照班好一些。但还需将两个班的成绩进行独立样本T检验,从表6所示的独立样本T检验可以对比两个班的成绩水平是否有显著差异,经过方差方程的Levene检验,接受方差相等的假设,说明方差齐性。取方差齐性时的假设,方差相等时的P值为0.021<0.05,因此可看出实验班与对照班在问题维度的测试成绩有显著差异。通过综合分析,得出实验班问题维度的素养水平优于对照班。
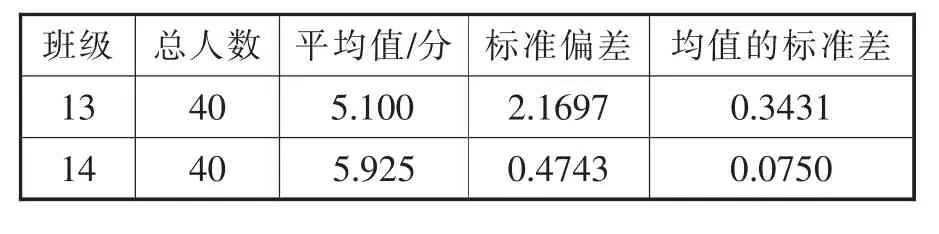
表5 实验班与对照班关于问题维度测试结果的统计量分析
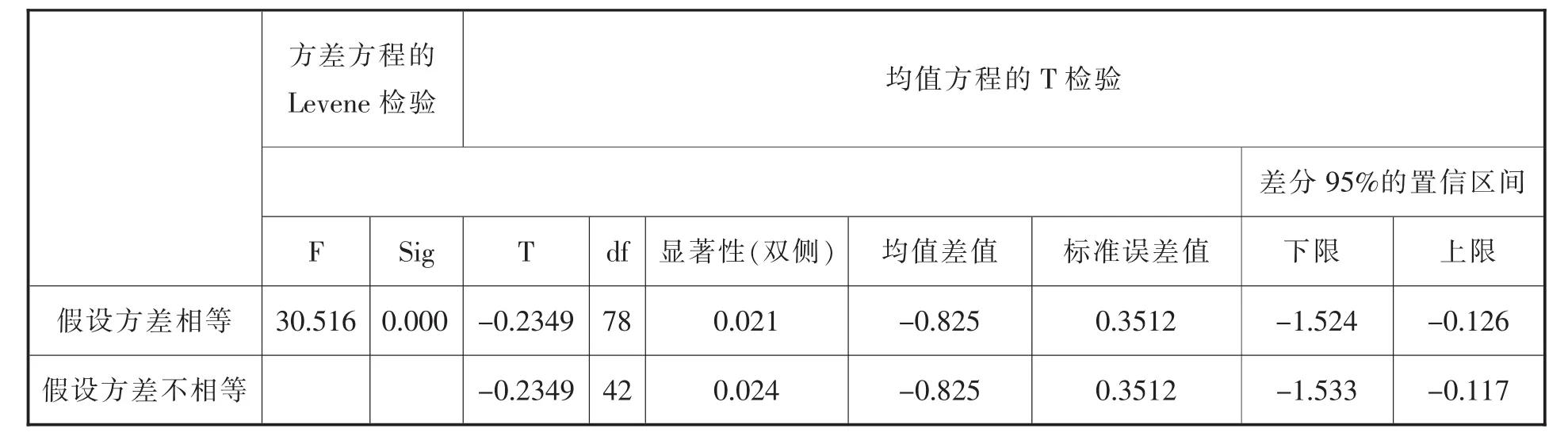
表6 实验班与对照班关于问题维度测试结果的独立样本T检验
通过SPSS22.0对实验班和对照班关于证据维度的成绩进行数据处理,根据表7可以比较两个班的均值,会发现实验班的均值明显高于对照班的均值,初步发现实验班经历过基于STEM教育的物理教学设计的学习后,证据维度的素养水平明显高于对照班的素养水平。进一步分析表8的独立样本T检验结果,经过方差方程的Levene检验,接受方差相等的假设,说明方差齐性。取方差齐性时的假设,方差相等时的P值为0.000<0.05,因此可以认为实验班与对照班的物理科学探究素养的证据维度的成绩存在显著差异,说明实验班的证据素养水平高于对照班。
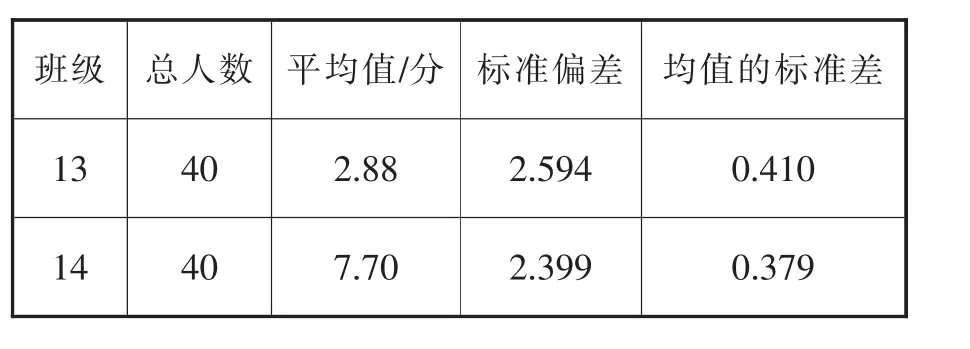
表7 实验班与对照班关于证据维度测试结果的统计量分析
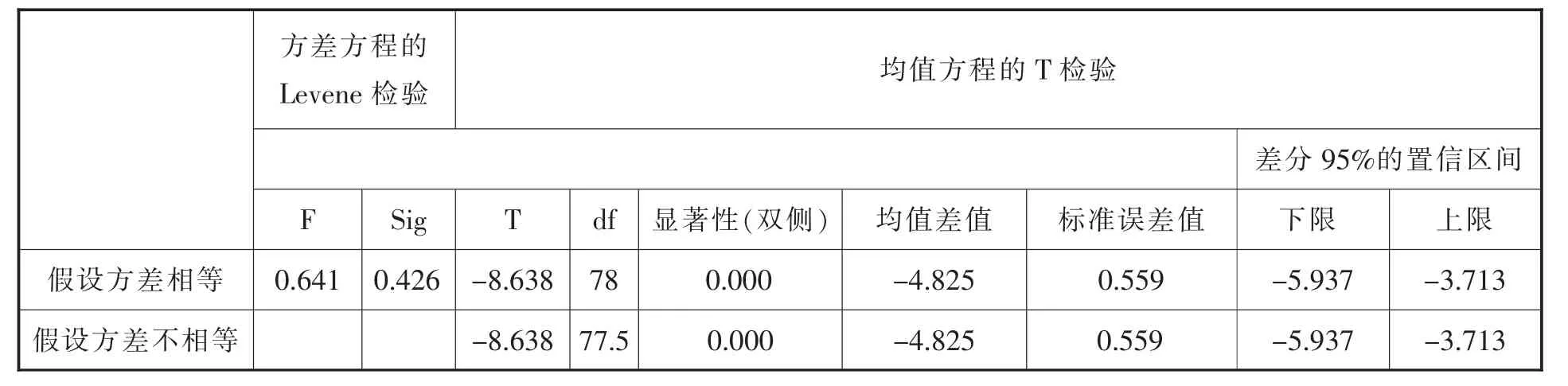
表8 实验班与对照班关于证据维度测试结果的独立样本T检验表
通过SPSS22.0对实验班和对照班关于解释维度的成绩进行数据处理,得到如表9所示的实验班和对照班的均值,对照班的均值比实验班的低,初步论定实验班在解释维度的成绩高于对照班,但是要确定两个班是否有差异,还需要进行独立样本T检验。再进一步分析表10,经过方差方程的Levene检验,接受方差相等的假设,说明方差齐性。取方差齐性时的假设,方差相等时的P值为0.001<0.05,因此可以认为实验班与对照班关于科学探究素养解释维度的素养水平有显著差异,并且实验班的解释素养水平高于对照班的素养水平。
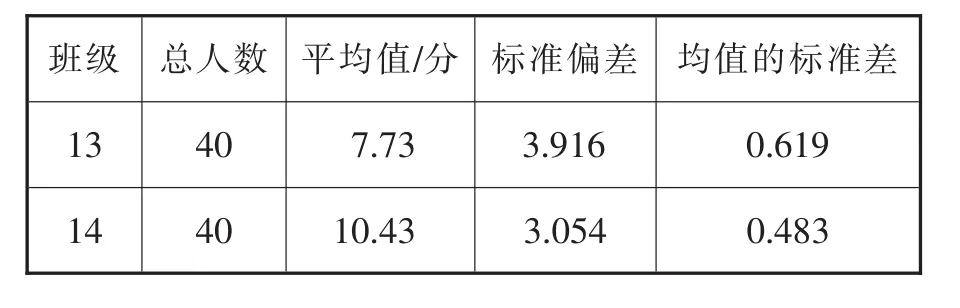
表9 实验班与对照班关于解释维度测试结果的统计量分析

表10 实验班与对照班关于解释维度测试结果的独立样本T检验
综上分析,发现实验班与对照班的成绩有显著性差异,且实验班的成绩优于对照班的成绩,初步得出实验班的科学探究素养水平高于对照班。可以看出基于STEM教育的高中物理教学模式能增强学生动手能力的同时,可以一定程度上提升学生的科学探究素养,让学生真正在探究中学习科学,动手实践。
4 结论
STEM教育由于其强调工程思维及动手实践的特点,实现了从项目制作中培养学生的科学探究能力的目标,为我国高中物理教学改革提供了一条可行之路。基于STEM教育的高中物理教学,凸显了教学的探究性。不仅强调让学生掌握方法,更看重让学生在亲身探究过程中发现问题,解决问题,获得知识。本研究所构建的教学模式主要有四个环节,分别是:“创设现实问题情境—以情境为主线进行科学探究—教师补充相关物理知识概念—优化解决方案进行工程制作”。将本教学模式应用于教学实践中,取得了较好的教学效果,能比较有效地提高学生的科学探究素养水平。
