瞬变电磁法三维模拟计算研究进展

薛国强,常江浩,雷康信,陈 康

(1.中国科学院地质与地球物理研究所 中国科学院矿产资源研究重点实验室，北京 100029；2.中国科学院大学 地球与行星科学学院，北京 100049；3.中国科学院地球科学研究院，北京 100029；4.青海省第三地质勘查院，青海 西宁 810000；5.河北地质大学 河北省战略性关键矿产资源重点实验室，河北 石家庄 050031；6.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038)

0 引 言

瞬变电磁法(Transient Electromagnetic Method，TEM)具有纯二次场观测、施工效率高等特点，在金属和非金属矿、工程地质和煤田水文地质等领域得到了广泛应用。该方法发射信号频带宽、频谱信息丰富，一次激发可覆盖探测所需的频段[1]。由于探测环境越来越复杂，发展瞬变电磁场精细模拟方法就变得更加重要[2]。

自20世纪70年代开始，国内外学者就开始研究瞬变电磁法响应的一维正演模拟。一维正演模拟采用的思路一般是先在频率域采用分离变量法解出层状介质条件下的频域电磁响应，然后将频域电磁响应转变到时间域。朴化荣通过快速Hankel变换求解贝塞尔函数得到一维模型在频率域的解，并采用G-S逆拉氏变换法将电磁场从拉普拉斯域转换到时间域，实现了瞬变电磁响应一维正演[3]。一维层状模型只适用于简单的地层结构；对于局部异常和复杂目标体的分析，则需要利用高维数值模拟的手段，根据不同的地质条件建立模型，以便获得更加符合实际情况的电磁响应[4-7]。

Kuo等采用二维有限元法对实际矿体模型的瞬变电磁响应进行了研究[8]；Oristaglio等利用二维DuFort-Frankel 有限差分法阐述了瞬变电磁场在二维地电断面下随时间扩散的过程[9-10]。Liu等采用异常场的DuFort-Frankel有限差分格式对二维线源的瞬变电磁响应进行了数值模拟[11]。但是从实际观测的模型角度来考虑，瞬变电磁法测量通常获得三维数据体。为了能够更加准确地了解地下介质的真实电性结构，二维瞬变电磁响应模拟计算则稍显不足。

随着计算机技术的发展，瞬变电磁法的三维正演问题逐渐成为国内外学者研究的热点。瞬变电磁场三维正演模拟主要有两种思路。一种思路是直接在时间域中求解，采用的算法主要包括时域有限差分法[12-13]、时域有限元法[14-16]、积分方程法[17-19]等。直接时域求解算法的时间步进方式分为显式方法和隐式方法：显式方法一般采用DuFort-Frankel步进格式，其时间步长需要满足稳定性条件限制；隐式方法一般采用向后Euler法，其时间步长不受稳定性条件限制，但每一时间步长需求解大型线性方程组。另一种思路是先采用数值模拟方法在频率域或拉普拉斯域求解，然后通过傅里叶反变换或拉普拉斯反变换将结果转换到时间域[20]。频率域求解的方法包括积分方程法[21]、有限元法[22]等。此外，也有许多学者采用虚拟波场域求解或者Krylov子空间算法进行瞬变电磁场三维模拟[23-24]。

加强资源与环境领域地球物理精细探测研究可支撑国家安全和社会稳定。受地质构造及火山活动的影响，金属矿形成过程一般经过强烈的岩浆活动和构造变动，成层性较差，而且一般在空间上规模较小，空间三维展布情况复杂。例如，对于煤矿而言，陷落柱、隐伏导水断层等三维复杂地质体是影响煤矿安全生产的巨大隐患。总之，由于地质结构多变，电磁场传播机制复杂，目标体的埋藏深度大，加上地表条件恶劣，瞬变电磁数据解释面临多解性、弱信号和强干扰的影响，瞬变电磁法三维模拟中采用简化公式，同时兼顾计算效率和计算精度成为难题，三维正演模拟的效果和效率也面临越来越多的挑战。有限差分法可以在一定程度上恢复时间域瞬变电磁场的因果关系，但计算域(几何区域)复杂度适应性较差；有限元法和有限体积法对计算域(几何区域)复杂度适应性较好，但计算量较大。进一步改善瞬变电磁模拟方法，实现地下三维地质体的电磁响应高保真恢复，对推进瞬变电磁法的进步具有重要理论意义，对实现地下矿体或者灾变体的预测定位具有现实意义。基于此，本文将系统梳理瞬变电磁法三维正演模拟的最新研究进展，分析采用有限差分法和有限元法进行三维数值模拟面临的关键技术问题，进一步指出瞬变电磁法三维数值模拟的未来发展方向。

1 三维正演计算方法

近年来，随着计算机技术的发展，越来越多的数值算法被用于瞬变电磁场的正演模拟，主要包括有限差分法、有限元法、积分方程法和有限体积法。

1.1 有限差分法

有限差分法是一种将求解域划分为差分网格，用有限个网格节点代替连续求解域的方法。有限差分法将磁场和电场在空间和时间上采取交替采样的离散方式进行分析。其采用的三维网格单元如图1所示[25]。Yee网格单元将磁场分量置于各面的中心，将电场分量置于各棱的中间(图1)，这样的网格方式使场分量在突变面上的连续性条件得到自然满足，有利于复杂结构的计算。有限差分法的优势是不需要求解大型方程，因此，其求解速度快且能够较好地实行并行运算。

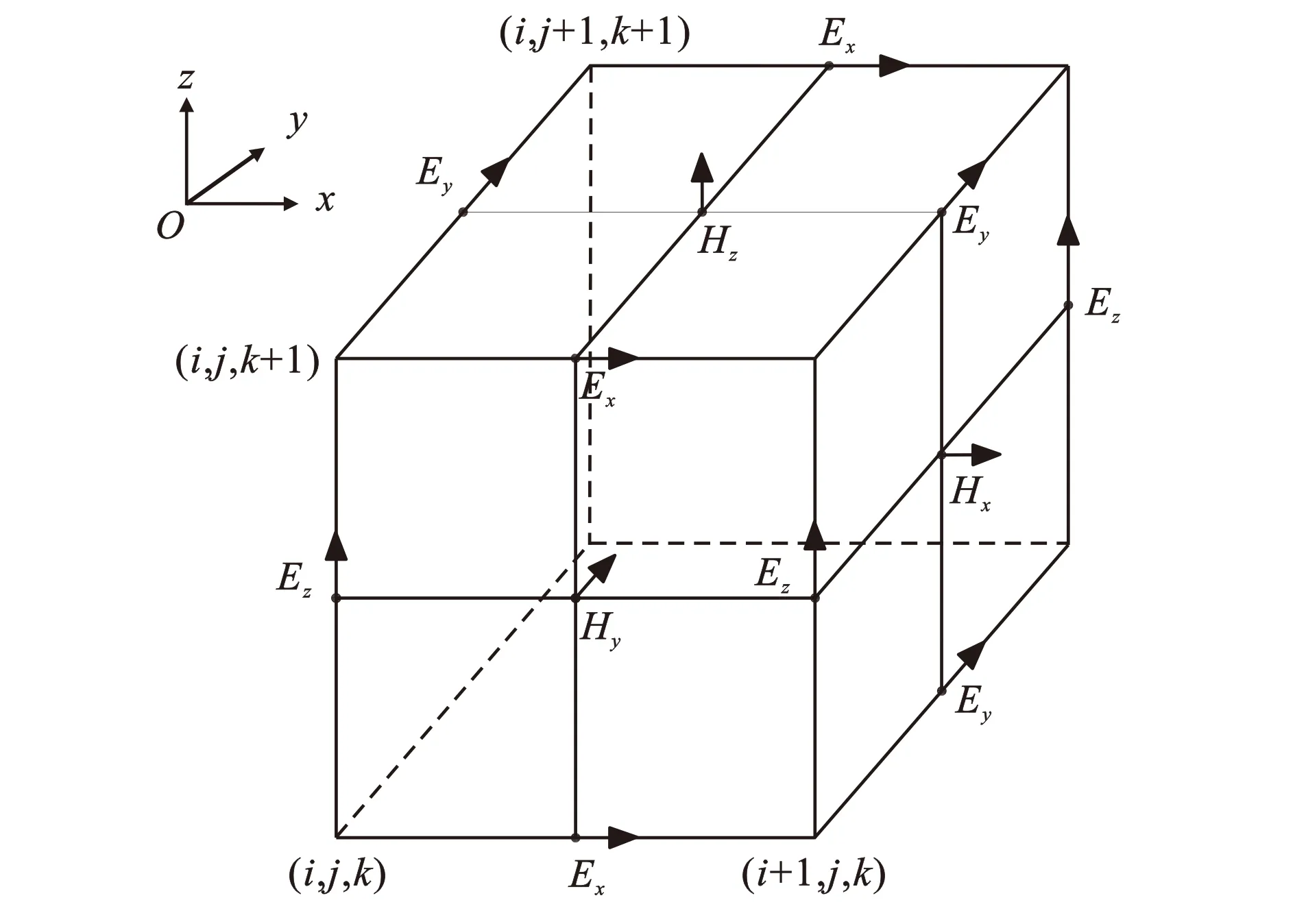
i、j、k分别为x、y、z方向网格剖分的节点；Ex、Ey、Ez分别为x、y、z方向上的电场分量；Hx、Hy、Hz分别为x、y、z方向上的磁场分量；图件引自文献[25]图1 有限差分网格剖分Fig.1 Staggered Grid of Finite Difference Method

为了将有限差分法应用于瞬变电磁场的模拟，Wang等采用虚拟位移电流代替位移电流的方法来处理磁场旋度方程[12]。其采用的电磁场方程为

(1)

(2)

(3)

(4)

式中：B为磁感应强度；H为磁场强度；E为电场强度；σ为介质电导率；J为传导电流密度；γ为虚拟介电常数；t为观测时间。

该算法的基本原理是：①采用准静态方程，并引入虚拟位移电流项突破常规差分方法稳定性条件的限制；②利用发射电流关断后一个非常小时刻在均匀半空间产生的解析解作为电磁场初始值；③地空边界条件采用位场向上延拓的方法避免对空气进行网格剖分；④对磁场进行散度约束以提升晚期计算精度。

针对带地形问题，在Wang等提出的算法[12]基础上，Endo等利用坐标变换的方法实现了带地形模型的三维正演计算[26]。针对电性源瞬变电磁响应计算问题，以Wang等提出的算法[12]为基础，Commer等直接求解电场的泊松方程以得到电流关断前的电场，实现了接地长导线源激发瞬变电磁场的三维计算[27]。Commer等还将有限差分法应用于含金属套管模型，在DuFort-Frankel有限差分法中开发了一个时间相关函数，以允许更大的迭代步长[28]。孙怀凤等将回线源加入有限差分计算，采用有源区域的差分方程对发射回线附近瞬变电磁场进行计算，实现了任意波形发射电流瞬变电磁场的计算[13]。李展辉等将卷积完全匹配层(CPML)边界条件应用于瞬变电磁场三维有限差分正演中，对卷积完全匹配层边界的吸收性能进行了分析[29]。Chang等将有限差分法应用于矿井全空间瞬变电磁场的计算，对煤矿典型富水区的瞬变电磁响应进行了模拟和分析[30-31]。

对于发射源加载问题，目前主要有3种方法：①利用发射电流关断后一个非常小时刻在均匀半空间产生的解析解作为电磁场初始值[12]；②取关断前建立的稳定场作为场的初始值[27]；③将源电流密度加入麦克斯韦(Maxwell)方程，一般采用梯形电流波形，也可设置为其他任意波形[13]。边界条件是影响晚期场精度的主要因素，有效的吸收边界不仅能提高解的精度，而且能减少网格数量。传统的有限差分模拟一般采用狄利克雷(Dirichlet)边界；随着研究的深入，目前的有限差分已经较多地采用吸收边界条件，大大提高了晚期解的精度。

随着研究的不断深入，有限差分法目前仍面临着很多问题：①在时间迭代上采用的是显式差分格式，计算量大；②只能采用结构化网格，限制了该方法的发展；③对于空气层的处理多采用向上延拓的地空边界，不能处理带地形模型；④在截断边界处多采用狄利克雷边界条件，影响晚期精度和计算速度。

1.2 有限元法

有限元法(Finite Element Method,FEM)是一种求解偏微分方程边值问题近似解的数值方法。它通过将求解域分解为有限个小单元，并在每个小单元假设一个合适的近似解，推导得到求解域内边值问题满足的线性方程组，从而得到问题的解。该方法由Turner等首次提出[32]，目的是解决弹性力学问题。Kuo等首先采用二维节点有限元法对低阻矿体在低阻屏蔽层下的瞬变电磁响应进行了模拟[8]。之后，国内外学者对三维时域有限元进行了大量研究[33-34]。

对于电磁场问题，其采用的控制方程主要是电场的亥姆霍兹方程[8]

(5)

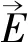
基于变分法可得到式(5)的变分方程，即

(6)

由式(6)可以看出，有限元法的基础包括变分原理及剖分插值。从变分原理来考虑，有限元法是Ritz-Galerkin法(加权余量法的一种)的变形，它选用“矢量基函数”克服了Ritz-Galerkin法在选取基函数时的困难。从剖分插值来讲，其实质是差分法的变形。差分法采用的是点近似，也就是说只考虑离散点的函数值，忽略了点的邻域内函数值变化，而有限元法是针对剖分后的小单元近似，考虑了一小段区域内函数值的连续变化。因此，有限元法一定程度上结合了Ritz-Galerkin法和有限差分法的优势。

Jin等分别运用标量有限元法和矢量有限元法对时间域和频率域响应进行了数值模拟；在求解常微分方程时，引入了一种基于Krylov子空间的Spectral Lanczos分解法，并通过实际地球物理问题以及均匀半空间解析解加以验证[35-36]。Börner等采用了一种高效的有限元算法，即首先利用矢量有限元求解得到频率域电磁场响应，再通过余弦变换求得时间域响应[37]；李建慧等在此基础上采用G-S变换进行了响应的时频变换，并获得了良好效果[38]。除了求解频域方程，有限元法也可以直接运用在时域求解，Börner等对该算法进行了改进：一方面是直接在时间域进行求解；另一方面是采用高阶有理Krylov方法求解相应的线性方程组[24]。针对复杂形状回线源问题，Li等采用非结构化网格将实际回线源剖分为电偶极子，实现了时域有限元计算[16]。针对电各向异性介质计算问题，Um等采用矢量有限元法研究了电各向异性条件下水平接地线源的海洋瞬变电磁响应特征[14]，之后又将该方法应用于垂直线源的瞬变电磁响应研究[39]。为了提高大型方程组求解速度，Fu等基于iChol分解和预处理共轭梯度(PCG)，采用一种并行迭代算法求解大型稀疏线性方程组，提高了计算效率[40-41]。Qiu等采用块状有理Krylov子空间算法加快了多源瞬变电磁响应的求解，并将其成功应用于海洋瞬变电磁响应计算[42]。Zeng等采用时域有限元法对瞬变电磁全发射电流波形的影响进行了研究[43]。有限元法虽然可以用非结构化网格离散求解域，有利于带地形或不规则异常体的正演，但仍面临许多问题。

(1)网格剖分问题。有限元法的计算精度和效率很大程度上取决于网格剖分的密度。当网格密度较大时，计算精度高，但计算效率低，因此，如何在保证计算精度的条件下提高计算速度是目前主要考虑的问题。

(2)时间离散问题。有限元法求解时域解的方式主要包括3种：一种是先求频域解，再通过时频转换技术得到时域解，计算精度受到时频转换技术的影响[44-45]；第二种是采用差分法直接在时间域求解，计算稳定性受到差分的限制[46]；第三种是基于有理Krylov子空间算法，计算精度和效率取决于模型电导率反差及子空间正交基的求解[24]。选择合适的时间方式，兼顾计算精度的效率对瞬变电磁响应的快速有效正演至关重要。

(3)方程组求解问题。方程组求解不仅决定了正演模拟结果的准确性，更决定了在采用向后差分或有理Krylov子空间算法时正演模拟的计算效率。目前常用的方程组求解方法主要是直接法，该方法计算精度较高，但是不适用于大型、超大型矩阵方程组的求解。而迭代法可用于巨型方程组的求解，但其精度及计算速度受到预条件的影响。由此看来，随着计算模型复杂化、多元化的发展，大型线性方程组求解对整个数值计算也十分重要。

1.3 积分方程法

积分方程法是最早实现三维电磁场模拟的数值计算方法，其只需要计算小体积异常区的场，不必计算整个区域的场。SanFilipo等采用时域积分方程法对均匀半空间中三维异常体产生的瞬变电磁响应进行了数值模拟[17]。Newman等采用积分方程法研究了层状大地中三维体的瞬变电磁响应，主要采用了先在频率域中求解，然后再转换到时间域的方法[21]。殷长春等将Cole-Cole模型引入积分方程正演计算，对瞬变电磁探测中激电效应的影响进行了研究[47]。

电磁场满足的频率域积分方程为

(7)

式中：EP是没有异常体时的场；σa=σb-σ1；G(r,r′,ω)为并矢格林函数。

将异常体区域剖分为N个小单元，假设在每个单元内电场为常数，则式(7)可离散为

En(r′,ω)dV′

(8)

将所有单元中心的电场方程写成矩阵方程，求解矩阵方程即可获得异常体内电场的分布。

积分方程法对内存需求较少，因此，其在数值计算早期比微分方程法具有更大的优越性。积分方程法的关键难点是求解复杂模型时格林函数的求解以及矩阵方程的求解。

1.4 有限体积法

有限体积法是一种基于物理量守恒的空间离散方法。该方法将计算区域离散为一系列规则或不规则的控制体积，在控制体积的离散网格上对待解控制方程进行积分，之后对积分式进行离散化处理得到离散方程组，通过求解该离散方程组从而得到数值解。该方法适用于任意类型的单元网格，对复杂边界形状的区域亦可满足边界问题的需要。与有限差分法相比，有限体积法精度不仅取决于对导数处理的精度，还取决于积分的精度，而且积分过程能够保证物理量的守恒特性。与有限元法一样，有限体积法也适用于结构化或非结构化网格。有限体积法在电磁场三维正演模拟中已得到较多的应用。Haber等采用有限体积法对瞬变电磁场进行计算，采用一阶向后Euler法对时间进行离散[48]。周建美等采用自然边界条件将电磁场控制方程转化为弱形式，采用结构化交错网格进行有限体积空间离散，实现了双轴各向异性地层回线源瞬变电磁三维正演[49]。

就离散方法而言，有限体积法可视作有限单元法和有限差分法的中间物。有限单元法必须假定值在网格点之间的变化规律(即插值函数)，并将其作为近似解。有限差分法只考虑网格点上的数值而不考虑值在网格点之间如何变化。有限体积法只寻求结点值，这与有限差分法相类似；但有限体积法在寻求控制体积的积分时，又必须假定值在网格点之间的分布，这又与有限单元法相类似。有限体积法的优点是可以用于不规则网格，且适用于并行计算，其存在的关键问题是精度提升困难，一般最高只能达到二阶精度。

2 研究展望

瞬变电磁法是在国内外广泛应用的近地表地球物理勘探方法，已经成为矿产勘察、水文地质调查等领域的重要方法[50]。对于复杂的三维地电结构精细勘探，一维甚至二维反演解释会造成虚假构造，有必要开展三维正演模拟研究，从而增加先验信息。

2.1 提高计算精度

目前瞬变电磁法的应用空间已经从地面扩展到空中、井下、隧道等，面临的环境更加复杂，空气层计算问题、井下多匝小回线源计算问题、金属设施影响下的计算问题等都需要三维正演计算来解决。瞬变电磁场计算与工程电磁场计算的主要差别是要求精度高，空间剖分范围大。在精度方面，有限差分法面临的主要问题是小尺寸目标网格剖分困难，空气层计算不稳定及晚期场受边界影响大等，主要解决思路是优化时间离散方案，采用高阶差分和多分辨网格，并采用合适的吸收边界条件；有限元法主要解决思路是网格加密，采用高阶插值基函数或高阶向后差分离散时间等。当然，也可以探索多种计算方法相互融合的新策略。比如，空间剖分采用有限体积法，对空气层进行同等剖分，一方面可解决地-空边界问题，另一方面可实现对地形的直接剖分模拟；时间迭代采用向后隐式差分，具有无条件稳定性；对电场和磁场的赫姆霍兹方程进行同样的处理，可分别得到高精度的电场响应分量和磁场响应分量；最终得到瞬变电磁三维多分量响应高精度正演计算结果。对于计算速度问题，可以从两个方面提升：一方面是减少算法本身的计算量，对于差分方法可以采取的改进思路是隐式差分或者将时间上的差分格式改为积分，但这同时将导致耗费内存的增多；另一方面是提升计算机硬件水平，加强交叉学科的研究，特别是加强与电磁场数值模拟相关的数学、计算机技术研究，在提高计算精度的同时，提升计算效率。

2.2 近场源电磁响应模拟

近年来，为了兼顾大深度和高精度探测的实际需求，近发射源探测模式成为国际上先进方法。短偏移距瞬变电磁法将接地导线源瞬变电磁法的测区由远区扩大到中、近区，即可以将观测点布置在离开场源0.5～2.0倍探测深度的地方，在此种情况下，观测信号较强，电磁场在地层中衰减较慢，提高了接地导线源瞬变电磁法的深部探测能力和分辨率，可一定程度上解决中国2 000 m以浅探测问题[51]。但由于存在深部电磁场自身的复杂性、观测环境的特殊性以及地质结构体的多变性等实际困难，还需要进一步突破瞬变电磁法在全场区精细探测方面的技术瓶颈，解决瞬变电磁场精确解、电磁噪声有效去除、深部目标体分辨等实际应用中的系列难题。而且，在近源开展时间域电磁法观测时，地层波的响应强烈且始终存在，如何有效区分地层波与地面波响应是目前拓宽短偏移距瞬变电磁法应用面临的一大困境[52]。

2.3 多源多分量响应模拟

目前，三维正演模拟计算技术还不足以支撑复杂地形、多发射源情况下多目标体短偏移距瞬变电磁响应精细模拟要求，因此，三维正演模拟还需进一步发展与下列问题有关的新算法。这些问题包括：①带复杂地形的短偏移距瞬变电磁模拟；②多发射源短偏移距瞬变电磁响应；③场源效应对短偏移距瞬变电磁响应的影响；④单一发射源、多发射源短偏移距瞬变电磁的记录点问题；⑤多复杂探测目标情况下单一发射源、多发射源短偏移距瞬变电磁响应；⑥各向异性介质条件下单一发射源、多发射源短偏移距瞬变电磁响应；⑦短偏移距瞬变电磁响应中的地层波与地面波响应等。因此，通过三维正演模拟新算法研究地层波的影响机理，其对不同场分量的影响程度(相对大小及范围)，以及不同目标(体电导及埋深)与地层波的耦合情况，可以为解决场源效应奠定良好的理论基础。

3 结 语

目前，主流瞬变电磁三维正演模拟算法包括积分方程法、有限差分法、有限体积法和有限元法。积分方程法的优点是只需要对异常区域进行离散，不必计算整个区域的场，其不足是求解复杂模型时会遇到某些更困难的数学问题，仅适用于简单模型电磁响应的模拟。有限差分法是一种直接将微分问题变为代数问题的近似数值解法，是发展较早且比较成熟的数值方法，其优点是不需要求解大型方程，因此，其求解速度快且能够较好地实行并行运算。有限差分法的缺点是其采用的显式差分步进格式需要满足稳定性条件限制，且只能采用结构网格，因此，其对计算域(几何区域)复杂度适应性较差。有限元法的优点是可以采用非结构化网格，可以更精确地模拟各种复杂几何结构，其缺点是需要求解大型方程。有限体积法可视作有限单元法和有限差分法的中间物，其可以用于不规则网格，且适用于并行计算，其缺点是精度提升困难，一般只能达到二阶精度。为了给三维反演提供可靠、快速的正演方法和模拟数据，三维正演的焦点主要集中在如何提升计算精度和计算速度。提升计算精度的关键在于优化时间离散方案、网格剖分方案，采用高阶离散也是未来的发展方向；提升计算速度的方向是采用并行计算和发展不同方法的组合算法。同时，考虑场源效应、各向异性等情况下的模拟计算也是今后的重要发展方向。

长安大学是我职业生涯的起点，也是我勘探电磁学研究的人生转折点！在母校七十周年华诞来临之际，通过一些铭刻在心的记忆片段来表达我对母校的热爱。同时，谨以此文祝贺母校生日快乐！1985年9月16日是一个下雨天，那天新生入学，从小没有出过远门的我在父亲的陪伴下从山西运城来到古城西安。头一次坐火车的我，以为火车跟汽车一样也没有厕所，尿急着憋了一路，也没吭声问父亲(从小到大，我有困难从不找家长)，还好只有四个多小时的车程。唉，难熬的第一次火车之旅！父亲把我送到宿舍安顿好后就要返回老家，由于我不认识校园里的路，更不熟悉校园外车水马龙的世界，我就把父亲送到宿舍门口，傻乎乎地看着父亲远去的背影。多年来总会为自己当年的幼稚和无知感到自责，也以此文表达对父亲的歉意。入学后，由于水土不服，我晚上“肚子疼”难以入睡，同宿舍的伙伴们很关切地问我怎么了，我一遍一遍给他们说老家话“我‘兔逗ten’，‘兔逗ten’”，但是没有一个人知道我到底哪里不舒服。此后的四年里，“兔逗ten”成为我们宿舍七个人的热词。还记得进入校门第一眼看到的标语是“欢迎你，未来的工程师”，当时感觉“工程师”这三个字很陌生；1989年7月22日，我毕业后被分配到山西一个煤田勘探单位进行野外工作，开始感觉这三个字很熟悉；1999年9月，我又考入母校攻读硕士学位，成为“二次回炉”的幸运儿，又一次沐浴母校的阳光，此时感觉这三个字很神圣。在母校六十年校庆的时候，我决定拿出自己的部分工资，以个人名义在地测学院发起“勤奋奖助金”，助力那些优秀的母校学子实现自己的梦想；随后，我担任了长安大学地球物理场多参数综合模拟实验室(中国地球物理学会重点实验室)副主任。无论我做什么工作，身在何方，心里都有一首谱写给母校的赞歌！