一种基于自适应方法的地震烈度圈自动勾画关键技术研究

刘 辉, 郭红梅, 黄丁发, 赵 真, 张 莹

(1. 西南交通大学 地球科学与环境工程学院, 四川 成都 611756;2. 四川省地震局, 四川 成都 610041)

0 引言

地震烈度是指地震引起的地面震动及其影响的强弱程度[1]。地震烈度受震级、震中距、震源深度、震源机制、地质构造、场地条件等多种因素的影响。一次地震发生后,根据建筑物破坏的程度和地表面变化的状况,评定距震中不同地区的地震烈度,绘出烈度等值线,即地震烈度圈,作为对该次地震破坏程度的描述。地震烈度圈的用途十分广泛,概括起来主要分为以下两个方面:(1)作为震害的简便估计。一次强震之后,政府或者社会为了了解震害的大小和分布情况,需要一个综合而简便的描述,便于了解各地区灾情[2];(2)对地震灾区灾情估计、抗震救灾工作和恢复重建工作具有十分重要的参考意义[3]。

目前最常见的做法是破坏性地震发生后,首先根据地震速报给出的地震参数,以微观震中为中心,利用区域烈度衰减模型快速算出预评估烈度圈,用于灾区面积的快速评估;然后应急队伍到灾害现场进行实地灾情快速调查获得烈度调查点;最后在预评估烈度圈的基础上结合烈度调查点,由专家使用GIS软件手动勾画得到最终烈度圈。这种传统勾画方式对星机地多源灾情信息利用不够,基本全部依靠人工实地调查,耗时耗力;手动勾画过程也对效率有影响。

针对烈度衰减模型对宏观震中和长轴走向考虑因素不够全面,可能造成较大误差,以及在后续烈度圈修正过程中对星机地灾情信息利用率不高,并全靠人工勾画,耗时耗力的问题,本文提出一种基于自适应算法的地震烈度圈自动勾画技术。充分考虑发震断层属性、居民地分布、余震展布等因素对宏观震中和烈度圈长轴走向的影响,在此基础上,采用自适应算法,将烈度与烈度圈面积统计关系作为约束条件,结合多源灾情信息融合后的离散烈度点数据,实现地震烈度圈的自动勾画,解决完全需要依靠专家手工勾画这一问题,提高烈度圈勾画的效率,可以为地震应急救援工作的快速开展提供支持。

1 技术路线及关键技术

充分考虑影响烈度分布的因素,首先通过微观震中、余震信息、断裂带属性、居民地分布和最高离散烈度点确定宏观震中位置,通过余震展布和断裂带方向确定烈度圈的长轴走向。在此基础上,以烈度与烈度圈面积的统计关系作为约束条件,结合星机地多源灾情信息融合得到的最高离散烈度点、宏观震中的包络线,利用自适应算法扩距,得到最高烈度圈。同样利用自适应方法在高一级烈度圈的基础进行扩距,并结合本级离散烈度点分布对烈度圈进行局部扩距,使得烈度圈包含所有本级离散烈度点,重复该过程,从高到低依次得到其他各级烈度圈。最后对生成的烈度圈进行平滑处理并进行精度评定。总体技术路线图如图1所示。

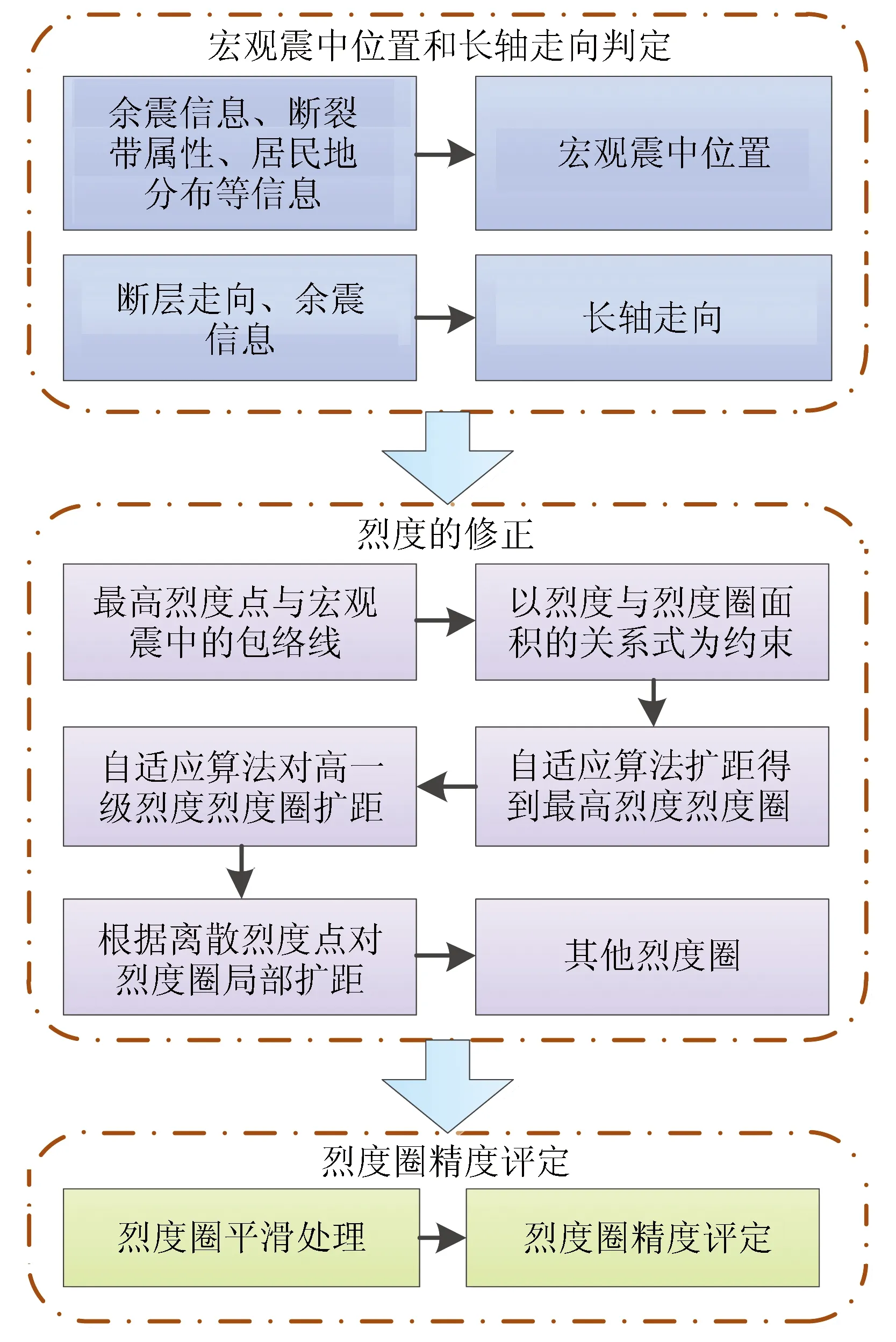
图1 技术路线图Fig.1 Thetechnology roadmap

1.1 宏观震中和长轴方向的确定

宏观震中是地震破坏最严重区域的中心,而微观震中是地震破裂初始点在地表的投影,两者之间可能发生偏离。李闽峰等[4]和刘吉夫等[5]对中国大陆历史地震宏观震中与微观震中的偏离研究得出:宏观震中与微观震中存在客观的不一致性。地震初期,烈度快速判定通常将微观震中作为初始输入参数,这会造成评估极震区与实际极震区的位置有偏差。极震区范围的圈定通常是地震专业人员参照微观震中,通过地震现场广泛、深入的实际调查后认定的,一般需要投入大量人力物力,且过程进展缓慢[6]。为此,一些学者对极震区的快速确定做了相关研究。胥广银等[7]利用地震动衰减关系、发震断层及其性质产状快速估计出了破坏范围,并指出应考虑地震破裂方式、地震地质灾害、人口经济分布等因素进一步指导抗震救灾;杨建思等[8]研究基于震源机制、震源破裂时空过程快速准确判断强震的极震区分布的方法和处理系统,建立了南北地震带基于公里格网人口、建筑、经济数据及其发展模型,实现了由地震地质加经济承载体在地震震源力作用下成灾的极灾区速判的思路;郑韵等[9]基于余震能量场空间分布,利用粒子群算法构造了一个震后6 h内包含所有主震区激发余震的面积最小椭圆作为估计极震区。基于上述研究,综合考虑微观震中、余震信息、居民地分布信息、断裂带属性、最高离散烈度点等信息估计极震区范围,然后取极震区的中心作为修正的宏观震中位置,具体流程图如图2所示。

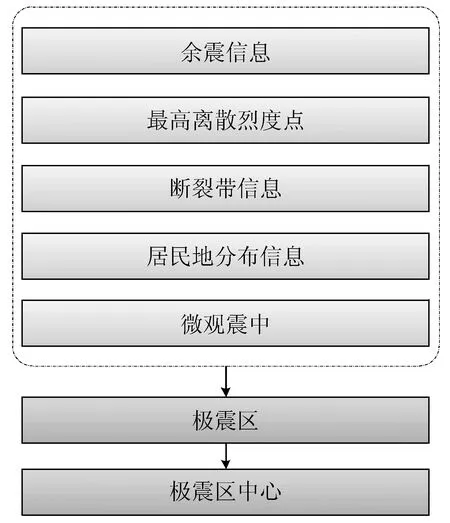
图2 宏观震中的确定Fig.2 Determination of macroscopic epicenter

烈度圈长轴走向是绘制烈度圈时的另一个重要的因素,长轴走向的准确与否直接会影响烈度圈的精度。秦娟等[10]通过对地震活动、活动断裂分布、震源机制解的统计特征分析,指出地震等震线长轴方位与活动断裂的走向、震源机制解的一个节面走向基本保持一致。曹刻等[11]在判断数字等震线模型的方向时,给出了不同断裂情况下,长轴方向的判断。张淑蓉[12]通过对地震序列的时空分布进行研究发现:主震宏观等震线的长轴方向和余震分布的长轴方向一致。此外汶川地震余震震中沿东北—南西方向展布[13-14],其分布方向与实际等震线的方向一致。本文结合断裂带走向和余震展布来判断烈度圈的长轴走向。

1.2 烈度圈面积分布规律

关于烈度区面积分布规律的研究,国内已有很多学者做过研究。陈培善和刘家森[15]利用逐步回归方法得到了震级与震中烈度、极震区面积的关系;余国政[16]利用历史地震资料,统计拟合了震级与烈度圈面积、烈度值、震源深度之间的关系。孙继浩[17]通过对烈度圈总面积和震级关系的分析得出烈度圈总面积与震级和烈度成指数关系。

经过对烈度圈总面积与震级和烈度的关系分析,本文采用孙继浩提出的烈度圈总面积与震级和烈度的关系式作为回归的数学模型,具体关系如下式:

S=exp(α-bI+cIM)

(1)

式中:S是I度以上烈度区的总面积,M是震级,a,b,c是回归系数。

本文收集了四川省1460—2019年震级在5.5级以上历史震例,将震级分为5.5～6.5、6.5～7.5和7.5～8.5三档,分别统计了烈度与烈度圈面积的数据,并以式(1)作为回归模型计算了每档的烈度与烈度圈面的关系,具体关系如下:

震级在5.5～6.5级之间,烈度与烈度圈面积关系为:

S=exp(15.578 6-3.541 4×I+0.343 2×I×M)

(2)

震级在6.5～7.5级之间,烈度与烈度圈面积关系为:

S=exp(18.381 9-4.147 3×I+0.380 8×I×M)

(3)

震级在7.5～8.5级之间,烈度与烈度圈面积关系为:

S=exp(13.760 7-3.459 8×I+0.335 4×I×M)

本文针对列车运营日计划编配问题，提出一种基于改进的最优-最差蚁群算法的车次与车组号匹配算法，实现车组均衡运用，为后续的列车运营日计划安排提供依据。

(4)

根据震级大小,选择对应档位的关系式计算不同烈度圈面积,例如当震级为7级时,利用式(3)可计算得到Ⅸ度烈度圈的面积为155.492 9 km2、Ⅷ度烈度圈的面积为684.234 0 km2、Ⅶ度烈度圈的面积为3 010.9 km2、Ⅵ度烈度圈的面积为13 249 km2。

1.3 基于自适应算法的烈度圈自动勾画

自适应是指处理和分析过程中,根据处理数据的数据特征自动调整处理方法、处理顺序、处理参数、边界条件或约束条件,使其与所处理数据的统计分布特征,结果特征相适应,以取得最佳的处理效果。由于自适应滤波器具有在未知环境下良好运行并跟踪输入统计量随时间变化的能力,所以广泛的应用于通信、雷达、声呐、地震学和生物医学工程等领域[18]。它通过自适应滤波算法调整滤波器系数,使得滤波器的特性随信号和噪声的变化而变化,以达到最优滤波的效果[19]。

自适应算法包含两个基本部分:滤波器和自适应控制算法。在滤波器中,给定输入向量u(n)和初始权重w(n),经过滤波器可以产生一个输出向量y(n)作为期望响应d(n)的估计,计算y(n)与d(n)的差值e(n);在自适应控制算法中,根据误差调整输入向量的权重,在滤波器中重新计算输出向量y(n),判断y(n)与d(n)的误差是否满足要求,若不满足,重复上述过程,直到e(n)满足要求为止。自适应算法原理图如图3所示。

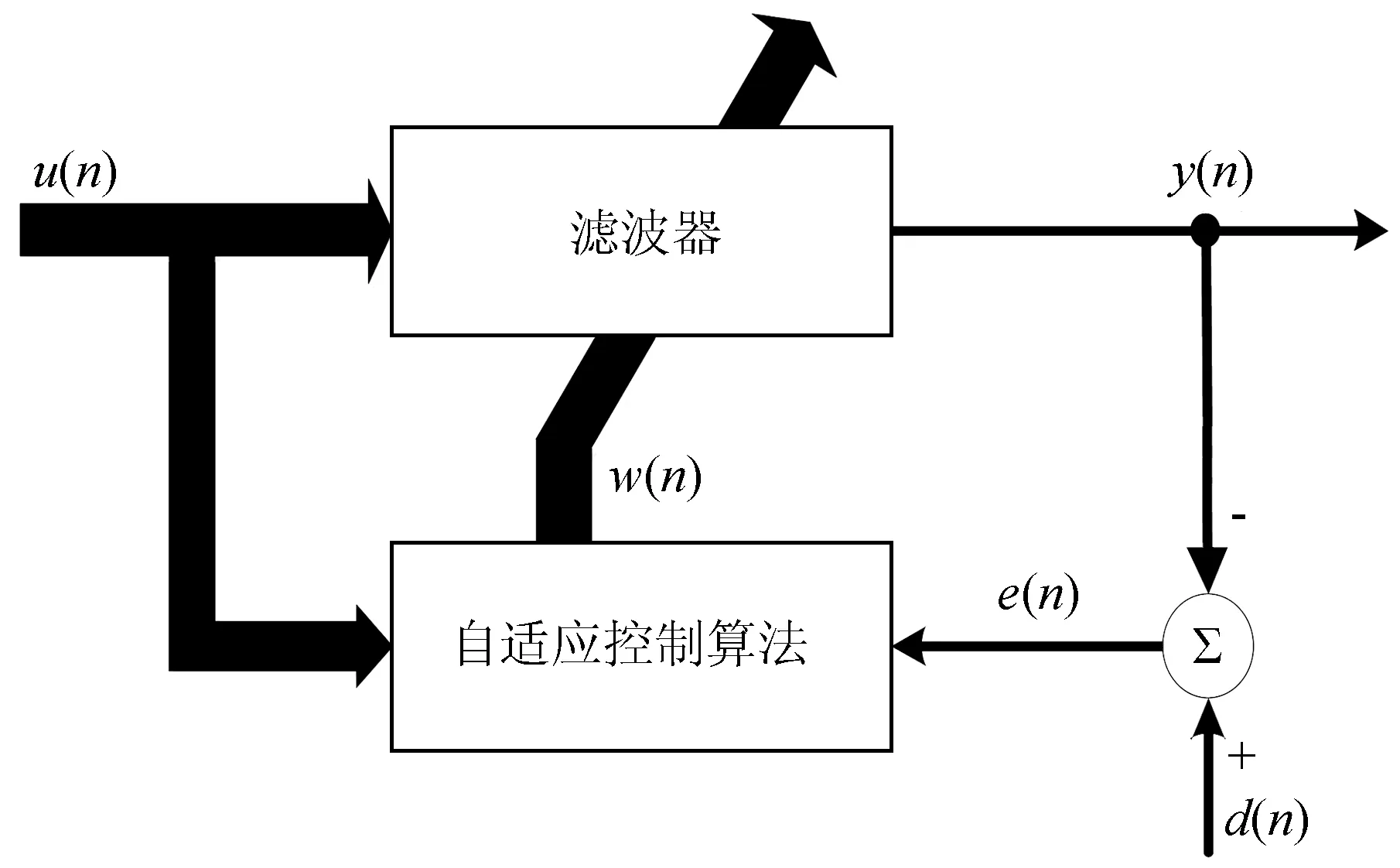
图3 自适应算法原理图Fig.3 The principle diagram of adaptive algorithm

采用自适应方法勾画烈度圈时首先勾画最高烈度圈。在确定宏观震中和烈度圈长轴方向的基础上,生成宏观震中与最高离散烈度点的包络线,将烈度与烈度圈面积的统计关系作为约束条件,在自适应算法中的滤波器中对包络线进行扩距,扩距的初值由最高烈度的统计面积与扩距后烈度圈面积的差值,除以最高烈度圈的边长确定,初次扩距完成后,计算最高烈度圈统计面积(期望面积)与扩距后的烈度圈面积差值的绝对值是否小于阈值,若未达到误差要求,则在自适应控制算法中用烈度圈统计面积与扩距后烈度圈面积的差值,除以扩距后烈度圈的边长更新扩距的距离,再进行扩距,重复上述自适应过程,直到扩距后的烈度圈面积与最高烈度圈的统计面积的误差满足要求时,此时得到最高烈度圈。最高烈度圈流程图如图4所示。

其余各级烈度圈是在高一级烈度圈的基础上,结合本级离散烈度点,以本级烈度圈面积同级关系为约束,由高一级烈度圈扩距得到的。由于烈度在衰减过程中沿长轴和短轴方向衰减具有不均匀性,因此在扩距之前要调整高一级烈度圈的长短轴比例。基于调整后的烈度圈利用自适应算法继续扩距,当面积达到目标烈度的烈度圈期望面积时,判断此时的烈度圈是否包含目标烈度的全部离散烈度点,若包含,则停止扩距;若不包含,则利用二分法确定扩距的距离,根据离散烈度点空间分布规律局部扩距,直到恰好包含目标烈度的全部离散烈度点为止,从而得到目标烈度的烈度圈。技术路线如图5所示。

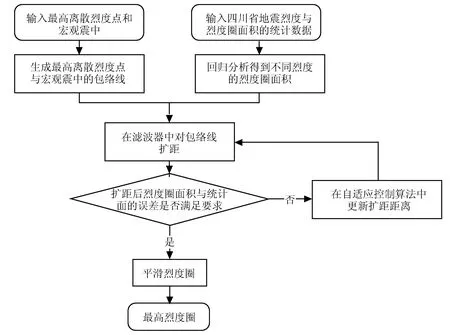
图4 最高烈度圈自动勾画技术路线图Fig.4 Technical route of automatic delineation of maximum intensity circle

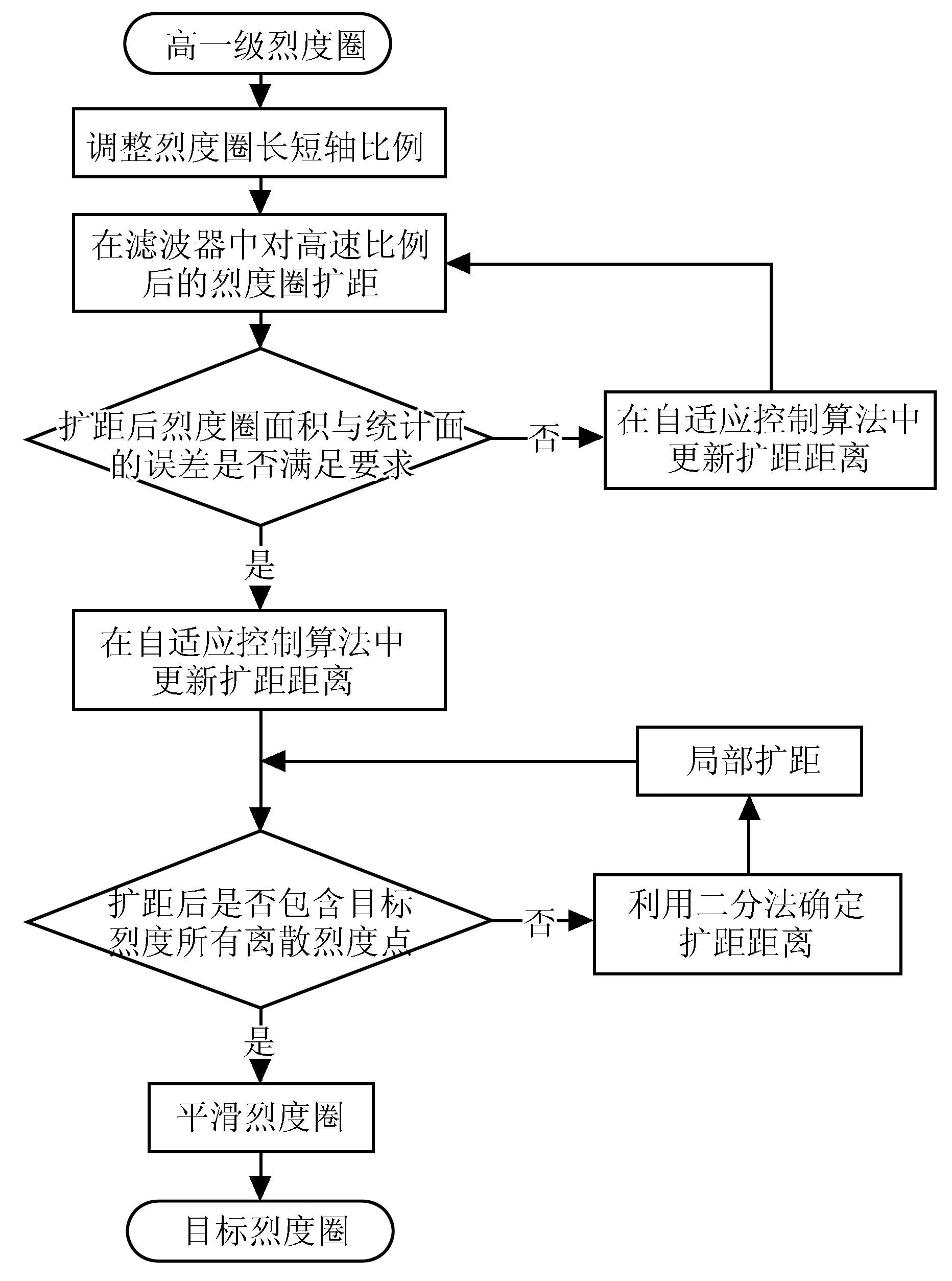
图5 烈度圈自动勾画技术流程图Fig.5 Technical route of automatic delineation of intensity circle

1.4 模型精度检验方法

本文采用两个精度指标来综合衡量模型的精度:(1)自动勾画烈度圈与实际烈度圈重合面积占自动勾画烈度圈面积的比例,它反映了自动勾画烈度圈的准确度;(2)自动勾画烈度圈漏判面积与实际烈度圈的比值,反映了自动勾画烈度圈漏判的误差。具体计算公式如下:

(5)

(6)

2 实验结果及分析

本文以四川省九寨沟7.0级地震为例,按照第1节的技术路线进行了实验,利用九寨沟地震震后获得的星机地灾情信息融合后的离散烈度点(图6),得到算法自动勾画的烈度圈,并对实验结果进行精度评定和误差原因分析。

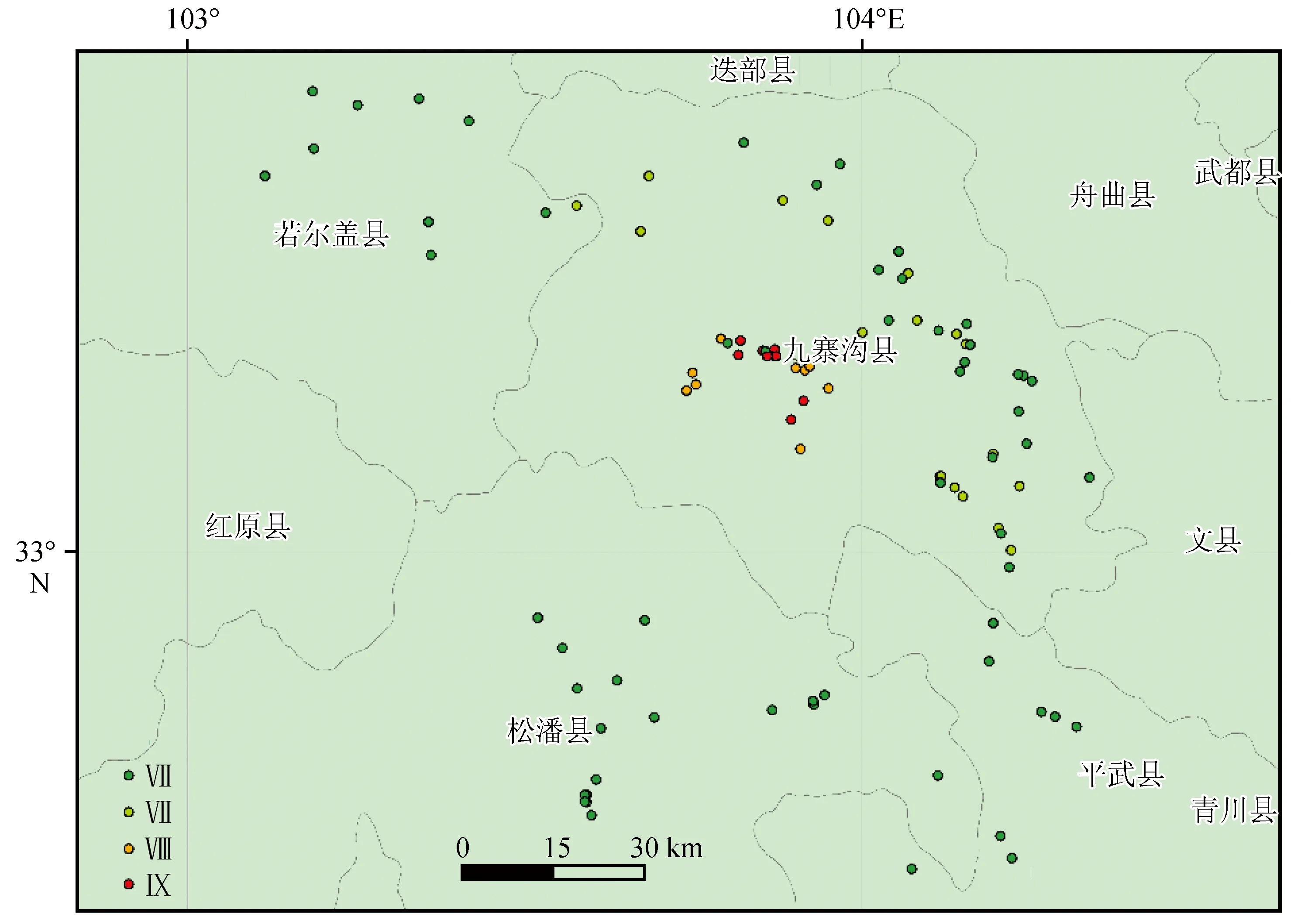
图6 离散烈度点分布图Fig.6 The distribution of discrete intensity points

2.1 宏观震中位置及长轴走向实验结果

首先基于余震信息、居民地分布信息、微观震中、最高离散烈度点确定了极震区,然后取极震区的中心作为修正的宏观震中位置,将距宏观震中最近的断裂带方向作为长轴走向。其实验结果如图7所示。从图7中可知实验确定的宏观震中与实际宏观震中较为接近,长轴走向与断裂带方向相同。

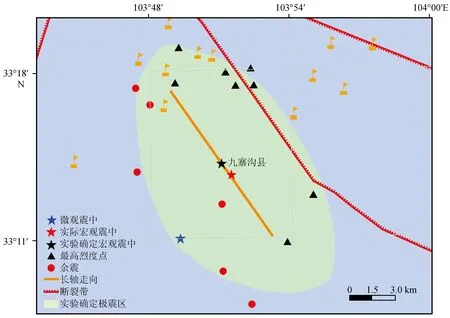
图7 宏观震中及长轴走向结果Fig.7 The result of macro epicenter and long axis trend

2.2 基于离散烈度点的地震烈度圈自动勾画实验结果

基于实验确定的宏观震中和长轴方向,结合最高离散烈度点生成包络线,将烈度与烈度圈面积作为约束,自适应扩距得到Ⅸ度烈度圈,在Ⅸ度烈度圈的基础上进行扩距,将统计面积和离散烈度点作为约束条件,可得到Ⅷ度、Ⅶ度、和Ⅵ度的烈度圈。实验结果如图8所示。从图8中可以看出,实验得到的烈度圈与实际烈度圈的形状相似大小相近,空间上的重合度较高且走向一致,说明由实验得到的烈度圈与实际烈度圈符合效果较好;其中Ⅶ度、Ⅷ度和Ⅸ度的烈度圈的形状与实际烈度圈的形状相似度较高,Ⅵ度烈度圈与实际烈度圈的形状相似度相对偏低。

图8 烈度圈自动勾画实验结果与实际烈度圈对比图Fig.8 Comparison between experimental and actual results of intensity circle

2.3 精度评定及误差分析

在进行结果的精度评定时,采用1.4小节给出的模型精度经验方法对生成的烈度圈的精度进行了精度评定,实验得到的烈度圈的精度如表1所列。

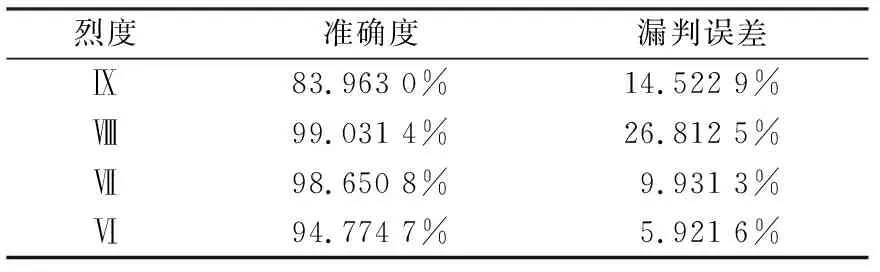
表1 烈度圈精度

由表1可知,就烈度圈的准确度来看,实验生成的烈度圈的准确度都在80%以上,平均准确度为94.105 0%;就漏判误差来看,实验生成的烈度圈的漏判误差都在30%以下,平均漏判误差为14.297 1%;综合准确度和漏判误差可以看出基于自适应方法的地震烈度圈自动勾画得到的烈度圈整体精度较好。

实验生成的烈度圈精度较好,但还存在误差,产生误差的原因可能有:(1)离散烈度点空间分布不均匀,导致扩距时对烈度圈的约束作用减弱;(2)算法中对经验数据过于依赖,未能更多的考虑本次地震的特征。

3 结论与讨论

提出一种基于自适应方法的地震烈度圈自动勾画方法,并以九寨沟地震为例进行实验,综合准确度和漏判误差对实验结果进行精度评定。实验结果表明:生成的烈度圈形状大小与实际烈度圈相似,空间的重合度较高,长轴的走向一致。但仍然存在误差,可能存在的原因及解决办法如下:

(1) 九寨沟地震星机地灾情信息融合后得到的离散烈度点空间分布不均匀,导致扩距时对烈度圈的约束作用减弱。针对这个问题,在应用中可以根据需要,通过星机地协同的方式实现全方位、空间较均匀的灾情信息采集,从而降低因烈度点分布不均造成的误差。同时,提供方便快捷的烈度圈修正工具,专家可以在自动勾画的基础上进行修正。

(2) 在得到最高烈度圈后,采用历史地震经验值改变最高烈度圈沿断裂带方向和垂直于断裂带方向距离的比例,再利用自适应算法进行等边扩距。由于经验值的主观性较大,可能会导致等边扩距得到的烈度圈有误差。下一步将进一步完善自适应算法,沿长轴方向和短轴方向扩距时,更多地考虑本次地震的特征,结合地震的震源机制、余震信息、地质条件等信息扩展不同的距离,降低对经验值的依赖程度。