垂直和平行于断层方向的脉冲参数特性分析
2021-05-13李华聪钟菊芳
李华聪, 钟菊芳
(南昌航空大学 土木建筑学院, 江西 南昌 330063)
0 引言
近断层地震动具有明显区别于远场地震动的典型特征,如上、下盘效应、方向性效应、速度脉冲效应、永久地面位移效应等,这些显著的近断层地震动特征导致建筑结构遭受严重破坏[1]。已有研究[2-3]表明,近断层区域内的工程结构承受高能量冲击,产生较大位移和变形与近断层地震动中的长周期速度脉冲有关。随着社会经济的不断发展,长周期构(建)筑物呈现出逐年增长的趋势,如超高层建筑、大跨度桥梁、大型储液罐等。开展近断层速度脉冲特性研究对揭示近断层区域的工程结构地震破坏机理以及开展抗震设防具有重要价值[4]。
速度脉冲特征主要由峰值、周期、峰值时刻、形状等参数来表征。国内外不少学者研究了速度脉冲的周期、峰值与震级、断层距、场地类别之间的关系,Somerville[5]对脉冲峰值和周期进行回归分析,给出了它们的衰减关系;Bray等[6]建立了基岩和硬土两种不同场地类别的脉冲峰值和周期关于震级和断层距的回归模型;刘铁林等[7]从NGA-West2数据库中筛选出126组近断层脉冲型地震动记录,研究了脉冲峰值和PGV/PGA与场地类别、矩震级以及断层距的关系。但仅有周期和峰值两个特征参数还无法确定一条完整的速度脉冲时程,还需进一步对速度脉冲的峰值时刻以及形状参数与震级、断层距、场地类别之间的关系进行探讨。
目前研究者通常关注垂直断层走向分量上的速度脉冲特性。已有研究[8]表明,在与断层走向不垂直的其他方向也存在着低频速度脉冲信号,并且某些结构和土体本身可能对双向水平地震动输入更敏感,因此有必要对平行断层分量上的速度脉冲特性进行深入分析。王宇航[9]通过对近断层记录进行分析,得到了水平分量与竖向分量的脉冲周期、峰值速度和峰值对应时刻的经验公式。由于震源机制、震源破裂过程、传播途径和局部场地条件等的不确定性,不同水平分量也会表现出不同的速度脉冲特性,但研究者忽略了这种差异性。谢俊举[10]采用小波分析识别出脉冲型记录,统计分析了脉冲幅值、周期与震级、距离的关系。该分析所采用的小波方法以峰值速度大于30 cm/s作为判断速度脉冲信号的其中一个条件,但这样的规定过于严格,某些不满足该条件的长周期速度脉冲信号可能被过滤掉。这些被过滤掉的速度时程依然具有明显的长周期特性,其对结构的影响作用同样不容忽视。
合理的等效速度脉冲模型能从复杂地震动记录中提取出脉冲成分[11],国内外学者对此开展了大量研究。本文首先对李晓轩提出的速度脉冲模型的适用性进行分析,按照波形匹配原则,从PEER强震动数据库的126组近断层脉冲型地震动记录中提取出脉冲特征参数,借助统计回归方法研究脉冲峰值、周期、峰值时刻、形状参数与震级、断层距、场地条件之间的关系,并比较垂直断层分量和平行断层分量的速度脉冲特性差异,该结果可为近断层速度脉冲特性研究提供一些参考。
1 速度脉冲型地震动记录选取
美国抗震设计规范以地表以下30 m处的等效剪切波速vS30作为场地分类依据(表1)。

表1 美国场地分类标准
近断层地震动一般是指距断层破裂面小于20 km范围内,地震波引起地表附近土层的强烈振动[12]。本文采用PEER强震数据库检索得到126组断层距小于20 km的脉冲型地震动记录,并按照美国场地分类标准将126组地震记录场地划分为基岩(A、B、C)和土层(D、E)两类(表2)。
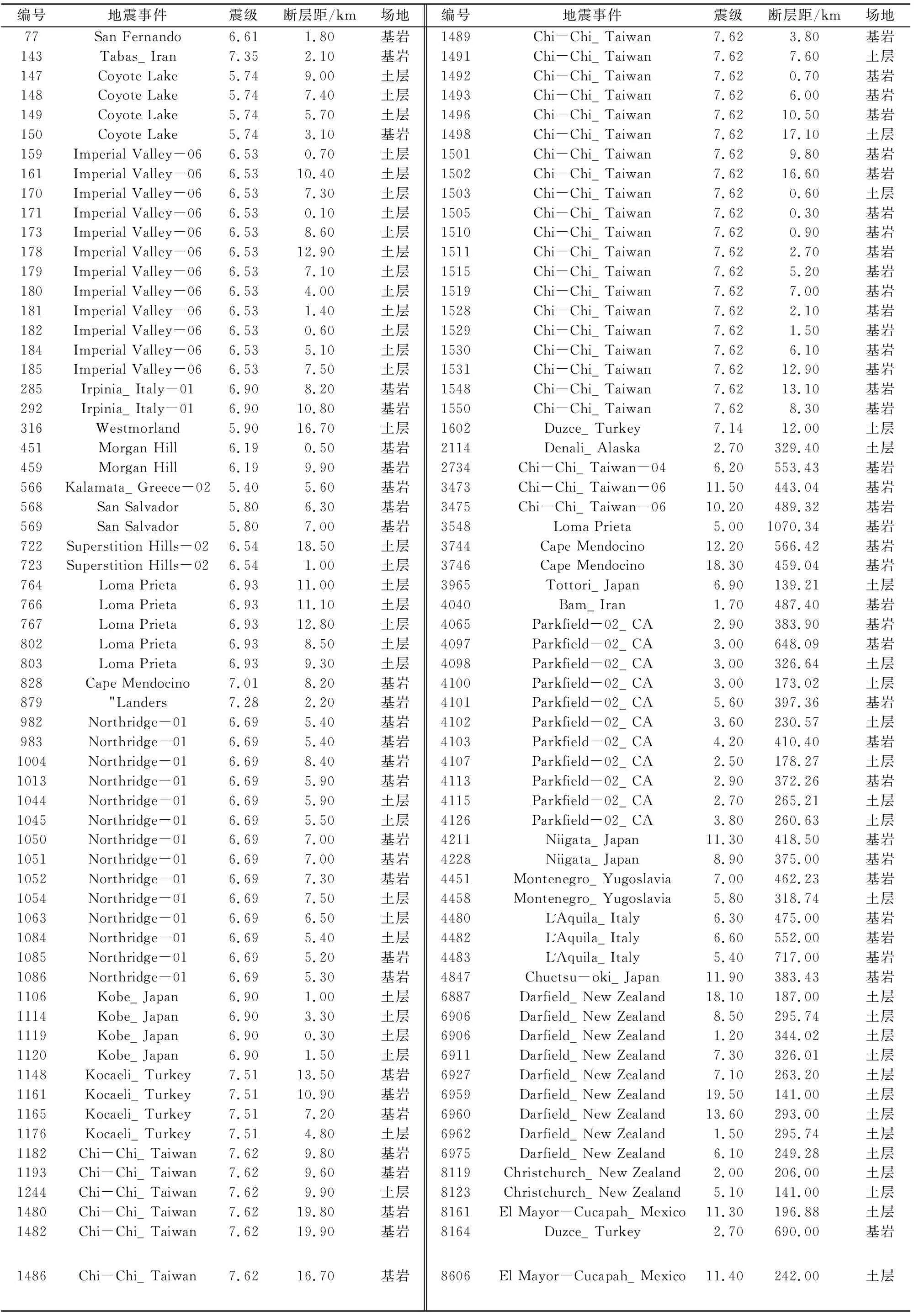
表2 126组近断层速度脉冲型地震动记录
2 速度脉冲参数提取
2.1 速度脉冲模型的选取
目前国内外学者提出的速度脉冲模型多采用矩形函数、三角函数(及其组合形式)、小波等形式。部分模型如下:
Menun等模型[13]:
(1)
Mavroeidis模型[14]:
(2)
Dickinson等模型[15]:
蒲武川等模型[16]:
(4)
李晓轩模型[17]:

(5)
式中:V(t)是速度;t是时间;Vp是脉冲峰值;Tp是脉冲周期;t0是脉冲的起始时刻;n1和n2是形状参数;t1是包络函数的峰值发生时刻;fp为脉冲频率;v是振幅模拟谐函数的相位;γ是振动特性参数;Nc是脉冲循环数;Tpk是脉冲峰值发生时刻;φ是脉冲相位,表示衰减率,其值大于1;Vp1和Vp2是脉冲正负峰值;ωp为脉冲的圆频率。
Menun等[13]提出的速度脉冲模型通过调整形状参数来模拟具有不同脉冲峰值的地震波,但是最多只能模拟2个周期的波形,并且参数较难确定。Mavroeidis[14]提出包络函数和余弦函数相结合的速度脉冲模型,该模型能考虑到脉冲波形的多样性,但参数v、γ不易确定。Dickinson等[15]提出的速度脉冲模型较好地拟合脉冲速度时程曲线,但模型是以脉冲峰值时刻为对称轴的对称图形,多数情况下与实际脉冲波形存在差异。蒲武川等[16]提出一种采用三角函数的速度脉冲模型,该模型适用于正负峰值存在差异的脉冲波形,但是不能模拟具有多个半脉冲的速度脉冲时程。李晓轩[17]考虑到脉冲峰值前、后半脉冲数量和峰值大小的不同,提出了指数函数和余弦函数相结合的分段函数模型,该模型能模拟多种不同形态的速度脉冲,并且在已知速度脉冲波形的情况下,形状参数唯一确定。相较于其他速度脉冲模型,李晓轩提出的模型考虑到速度脉冲全波形的不同形态,引入参数较少且易于确定,较好地实现了速度脉冲波形参数化,为近断层速度脉冲特性研究提供了一种分析方法。
在连续的多个半脉冲中,当相邻的半脉冲周期相差过大,无法完全拟合所有半脉冲时,李晓轩提出可以以脉冲峰值对应时间节点为分界将脉冲周期分为峰值前半脉冲周期(记为Tp1)和峰值后半脉冲周期(记为Tp2),这时,式(5)可改写成式(6):
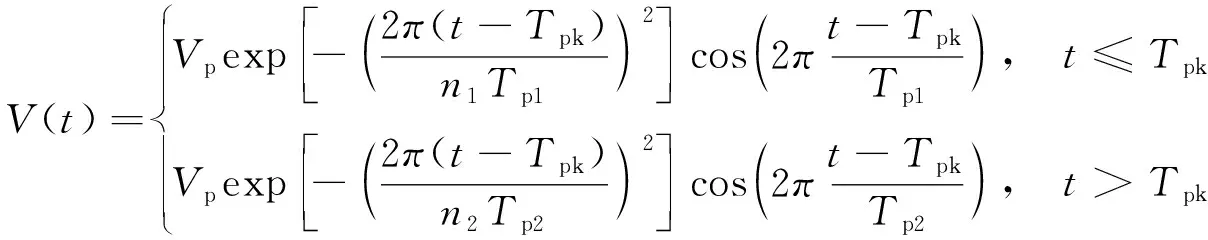
(6)
目前,大多数研究者都只关注速度脉冲峰值最大的主脉冲的相关特性,没有考虑半脉冲的周期和形状的变化对速度脉冲波形的影响。图1给出了不考虑和考虑峰值前、后半脉冲周期差异的脉冲时程拟合结果,对比图1(a)、(b)可明显看出,(a)图拟合得到的脉冲时程中峰值后的部分半脉冲信号丢失;(b)图拟合得到的脉冲时程将峰值后的半脉冲信号较为完整地表示了出来。显然,对于一条连续的速度脉冲时程,半脉冲相关特性同样值得关注。李晓轩模型[17]可将峰值前、后半脉冲周期分开考虑,其具有更强的适用性。
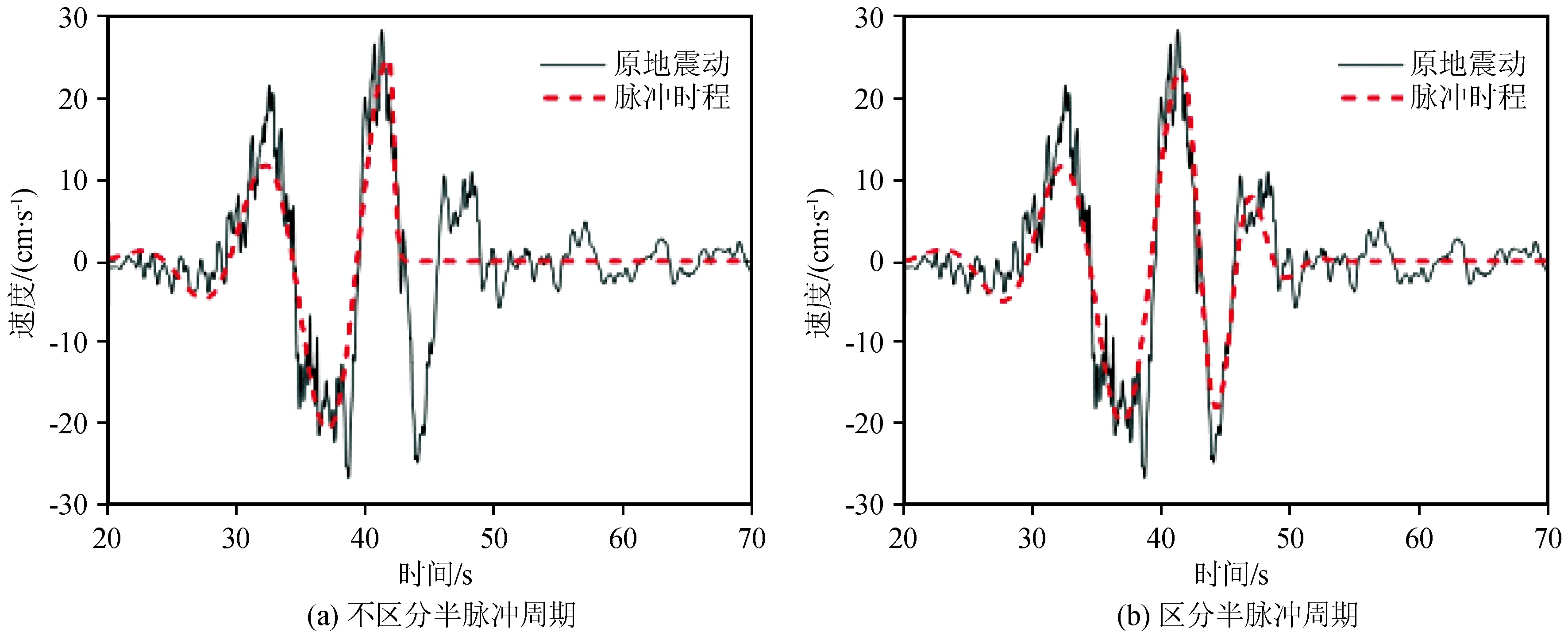
图1 脉冲时程拟合结果对比Fig.1 Comparison between pulse time-history fitting results
考虑到速度脉冲峰值前、后的波形通常具有不对称性,本文以脉冲峰值对应时间节点为分界,将速度脉冲分成峰值前半脉冲、峰值后半脉冲和主脉冲三类,分别讨论各类脉冲的周期和形状参数的变化规律,以期为近断层速度脉冲特性分析提供理论参考。
2.2 基于最小二乘法的速度脉冲模型参数的拟合
为了消除速度时程中高频成分对速度脉冲峰值Vp的影响,采用七点汉宁窗[18](加权值:0.036 6,0.125 0,0.2134,0.250 0,0.213 4,0.125 0,0.036 6)对速度时程进行平滑,直到正负峰值之间第一次出现且仅有一个拐点,即速度时程的二次导数在正负峰值之间第一次等于零且仅有一个零点时停止平滑。图2给出了平滑前、后的记录时程及速度脉冲时程的对比图。从图2中结果来看,平滑后的速度时程由于过滤了大多数高频成分而变得光滑,使低频脉冲成分较为完整地保留了下来。
1组实测地震记录通常包含1条竖直记录分量和2条相互垂直的水平记录分量,对其中2条水平记录分量按照平行四边形法则进行旋转变换,可得到水平任意方向的地震动分量,计算式如下[19]:
f(t,θ)=f1(t)cosθ+f2(t)sinθ
(7)
表3给出了所选取的126组近断层脉冲型地震动记录31次地震事件的断层走向。将所选取的各组地震记录的2条水平分量按照式(7)进行旋转变换,得到相应的垂直断层分量(记为FN)和平行断层分量(记为FP);利用最小二乘法拟合得到FN和FP分量的式(6)模型特征参数的最优解。
3 速度脉冲模型参数特性分析
采用非线性统计回归方法,分析了126组近断层脉冲型地震动记录FN和FP分量的速度脉冲峰值(Vp)、脉冲周期(Tp)、峰值时刻(Tpk)、形状参数(n)随震级(Mw)、断层距(R)、场地条件等的变化规律,建立相应的函数回归模型。
3.1 速度脉冲峰值特性分析
图3示出了Vp随Mw和R的变化情况,其中中国台湾集集地震TCU068台站的地震记录FP分量的Vp值高达204.15 cm/s,见图3(b)中加圆圈标注的点。集集地震断层北端显著的滑冲效应可能是引起该台站记录到的Vp明显增大的主要原因[14]。为了避免个别数据过大从而影响整体数据的回归结果,在后续的统计分析中将不采用这组数据。参考已有研究的统计回归模型[15,20],采用式(8)进行回归分析:
lgVp=a·Mw+b·lgR+c+ε
(8)
式中:a、b、c为拟合系数;ε为表示误差的随机变量,用回归标准差表示。
Vp随Mw和R变化的拟合结果如图4所示,回归系数列于表4,图5为FN和FP分量在不同场地条件下Vp随Mw和R变化规律的对比图。结合图4、5和表4可知,FN和FP分量的Vp均表现为随Mw的增大而增大,随R的增大而减小。随着Mw的增大,FN分量的Vp增长速率大于FP分量,基岩场地上的Vp增长速率大于土层场地,说明FN分量的Vp对Mw的敏感程度大于FP分量的相应值,基岩场地上的Vp对Mw的敏感程度大于土层场地的对应值。随着R的增大,FN分量的Vp衰减速率大于FP分量,基岩场地的Vp衰减速率大于土层场地,说明场地土质越软,Vp受R的影响越小。分析认为,导致FN分量和FP分量的Vp衰减速率出现差异的原因可能是地震波辐射方式的不同。
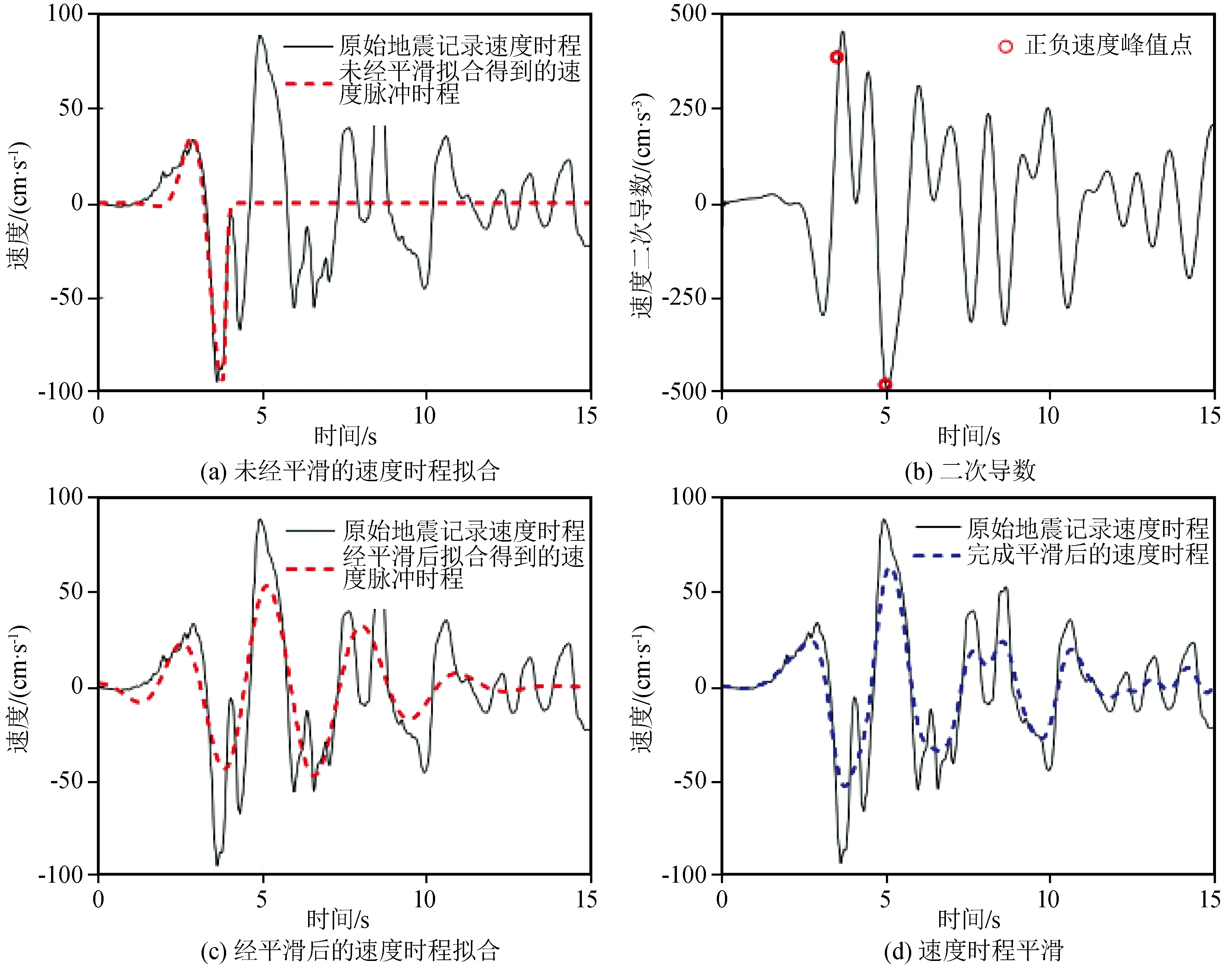
图2 平滑前、后的记录时程及脉冲时程对比Fig.2 Comparison of record time history and pulse time history before and after smoothing
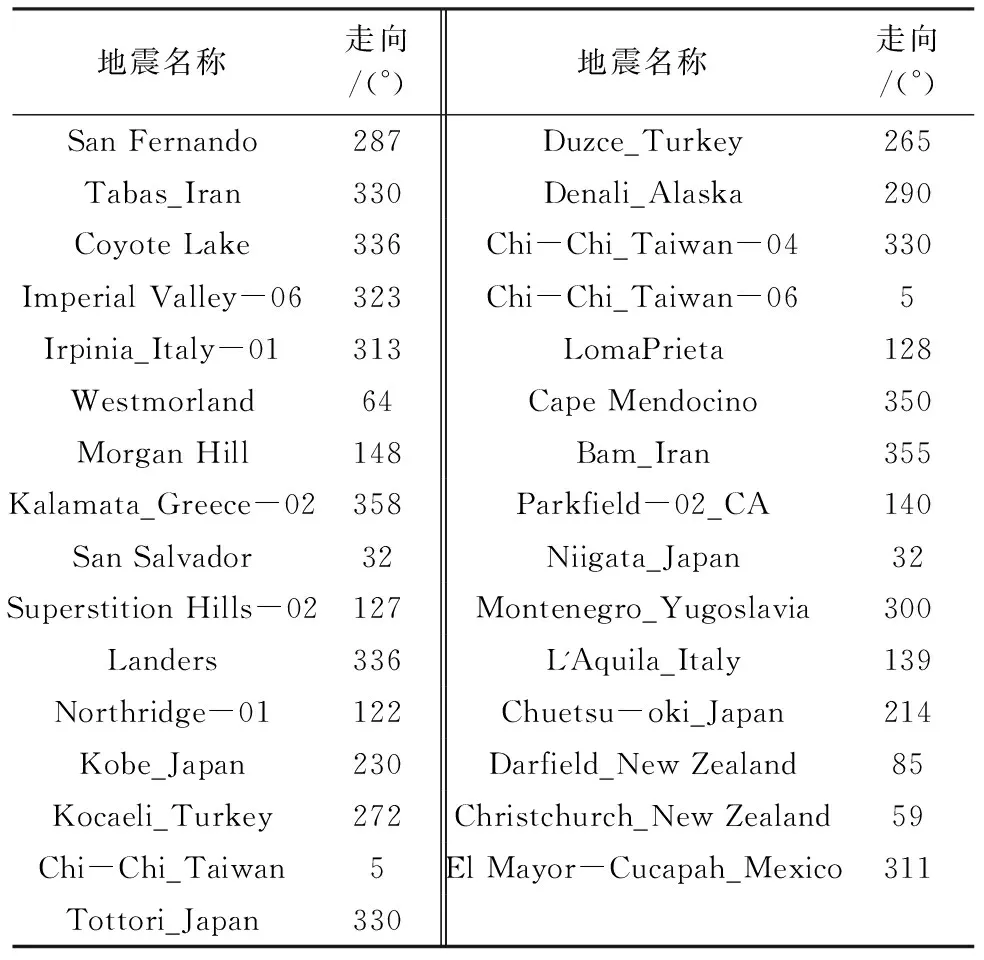
表3 31次地震事件的断层走向
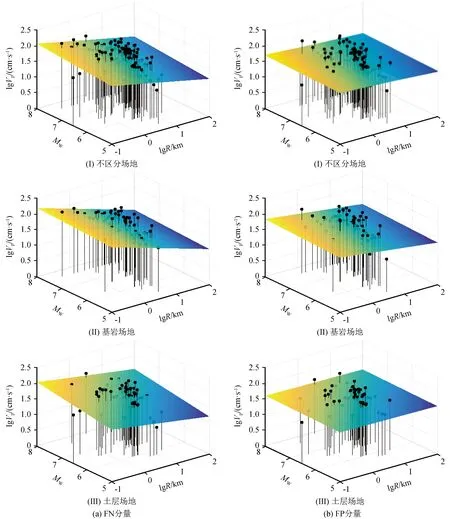
图4 脉冲峰值随震级和断层距变化的拟合结果Fig.4 Fitting result of variation of pulse peak with magnitude and fault distance
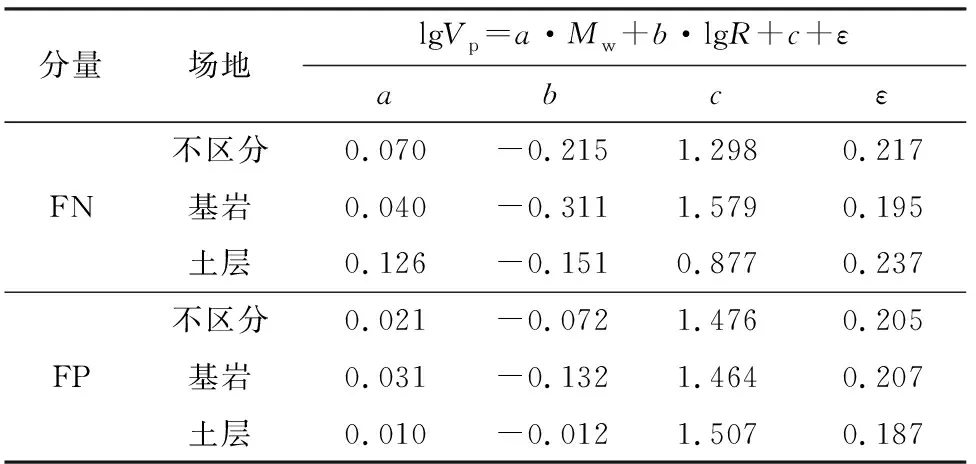
表4 脉冲峰值的回归结果
3.2 速度脉冲周期特性分析
3.2.1 速度脉冲周期相关性分析
为探究由Tp1、Tp2以及由峰点法[21]计算得到的主脉冲周期(记为Tp0)的相关性,采用式(9)进行回归分析,并用相关系数的大小来反映Tp1、Tp2与Tp0的相关程度,它们的相关性分析结果如表5和图6所示。
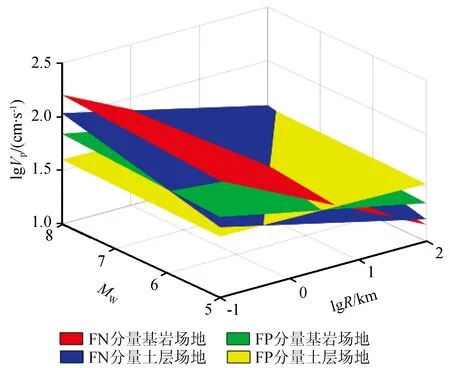
图5 脉冲峰值随震级和断层距变化拟合结果对比Fig.5 Comparison between fitting results of variation of pulse peak with magnitude and fault distance
y=a·x+b+ε
(9)
式中:a、b均为拟合系数;ε为表示误差的随机变量,用回归标准差表示。
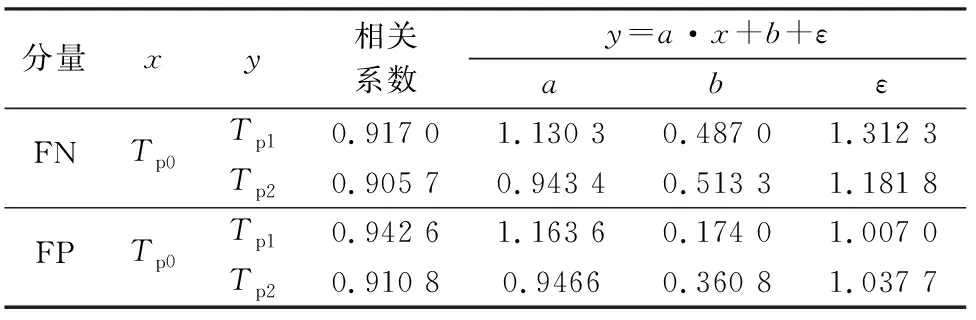
表5 半脉冲周期与主脉冲周期的回归关系
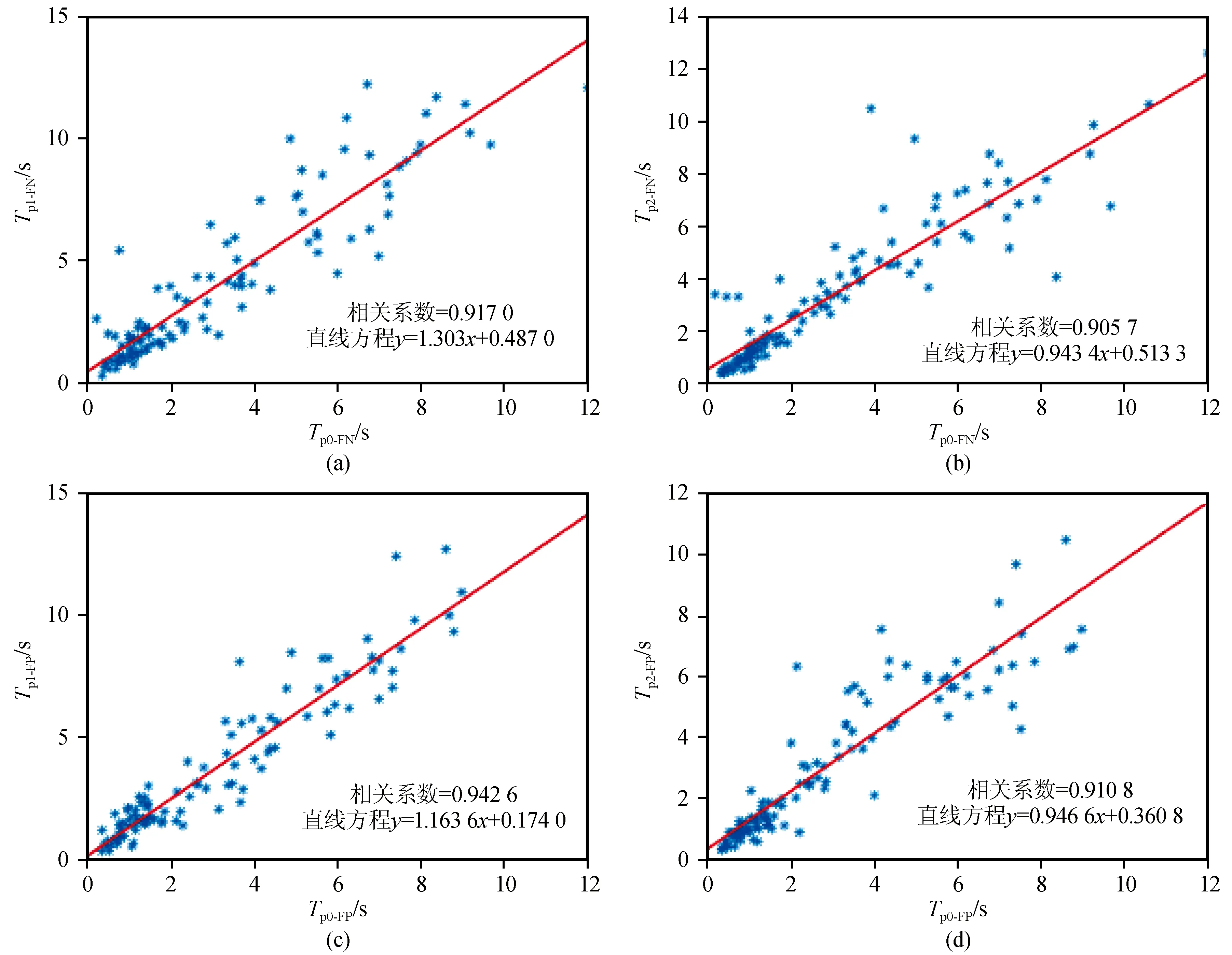
图6 半脉冲周期与主脉冲周期的拟合结果Fig.6 Fitting result of half pulse period and main pulse period
从表5和图6的结果来看,Tp1、Tp2与Tp0具有较强的线性相关性,相关系数均达0.9以上。FN和FP两分量的Tp1与Tp0的相关性均强于Tp2与Tp0间的相关性,这可能是由于峰值后半脉冲晚于峰值前半脉冲到达台站能量衰减更多所致。相较于FN分量,FP分量的Tp1、Tp2与Tp0的相关性更强,但总体来说,方向性差异不太明显。
3.2.2 速度脉冲周期变化规律对比分析
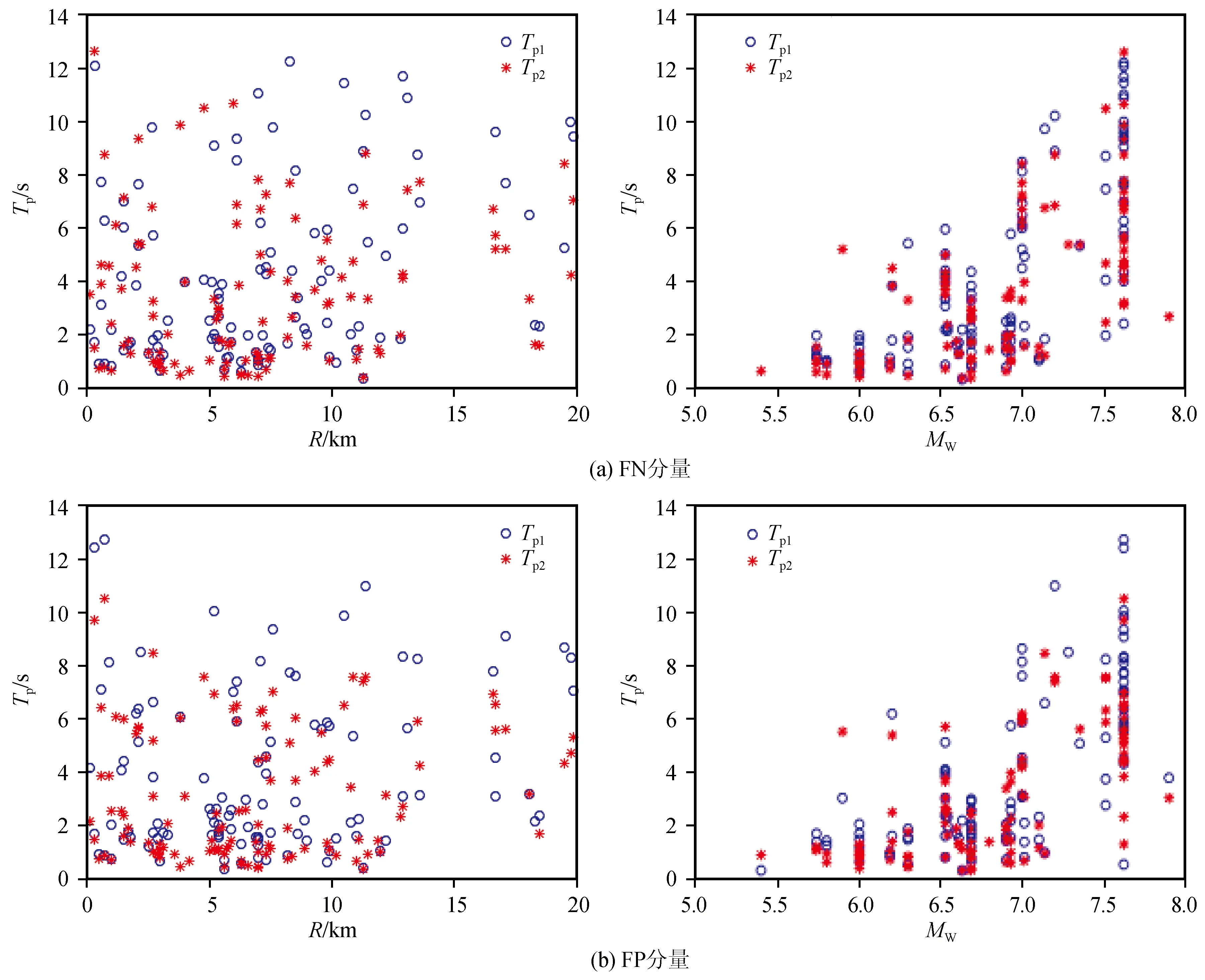
图7 脉冲周期随断层距和震级的变化Fig.7 Variation of pulse period with fault distance and magnitude
图7给出FN和FP分量的Tp随Mw和R的变化图。由图可知,Tp随R变化的规律性不强,Tp随Mw的增大呈指数增长。由于本文研究的是近断层区域(R<20 km)的速度脉冲特性,因此在研究速度脉冲周期时不考虑断层距R的影响。采用式(10)分别对Tp0、Tp1、Tp2进行回归拟合:
lnTp=a+b·Mw+ε
(10)
式中:a、b为拟合系数;ε为表示误差的随机变量,用回归标准差表示。
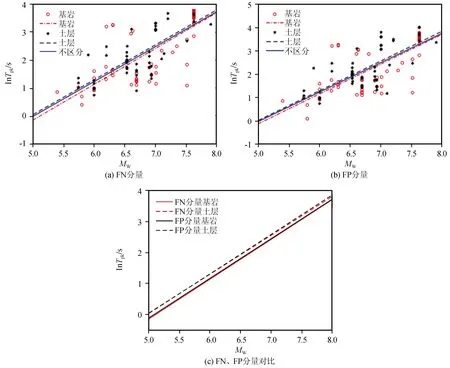
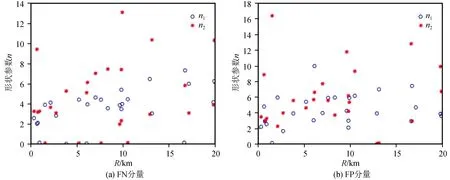
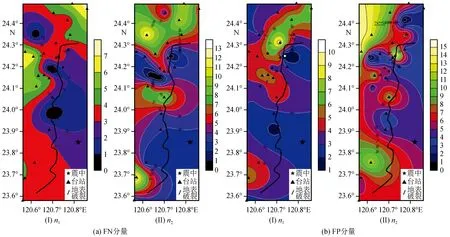
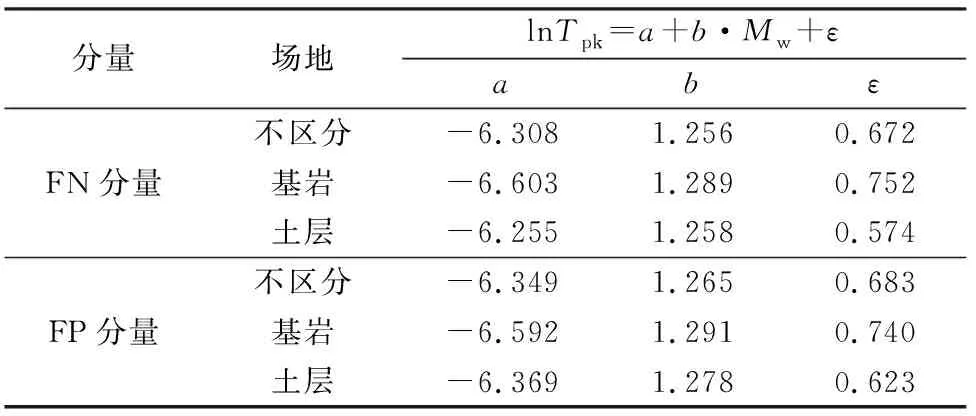
各类速度脉冲的Tp随Mw变化的拟合结果及其对比如图8所示,回归系数列于表6。由图8和表6的拟合结果可知:FN分量的lnTp1随Mw变化的斜率最大,lnTp2的斜率最小,lnTp0的斜率值介于lnTp1和lnTp2的值之间,说明Tp1对Mw的敏感程度最高,Tp2对Mw的敏感程度最弱,Tp0对Mw的敏感程度介于Tp1和Tp2之间。FP分量的lnTp1和lnTp0随Mw变化的斜率差异不大,但lnTp2斜率大于前两者,说明Tp1和Tp0对Mw的敏感程度较为接近,Tp2比Tp1和Tp0对Mw更为敏感。当Mw相同时,同一水平分量的各类速度脉冲的Tp存在差异,它们的大小关系可以归纳为:Tp1>Tp2>Tp0。当Mw>6.0时,FN分量的Tp0值大于FP分量的相应值,当Mw≤6.0时,FN分量的Tp0值小于FP分量的对应值;当5.0 表6 脉冲周期与震级的回归关系 图8 脉冲周期随震级变化的拟合结果及其对比Fig.8 Fitting result of variation of pulse period with magnitude and their comparison 在人工合成脉冲型地震动时,通常的做法是将高频成分和低频速度脉冲成分进行叠加。这就需要对地震发生后速度脉冲峰值发生时刻Tpk进行统计分析。图9分别给出了Tpk随Mw和R的变化图。由图9可知,Tpk随R变化的规律性不强,Tpk随Mw的增大呈指数增长,可采用式(11)对其进行拟合分析: lnTpk=a+b·Mw+ε (11) 式中:a、b为拟合系数;ε为表示误差的随机变量,用回归标准差表示。 速度脉冲的峰值时刻Tpk随Mw变化的拟合结果及其对比如图10所示,回归系数列于表7。从统计结果来看,基岩场地条件下,FN和FP分量lnTpk随Mw变化的斜率差异不大,说明基岩场地条件下,两分量Tpk随Mw的变化速度比较相近;在土层场地条件下,FP分量lnTpk随Mw变化的斜率大于FN分量的相应变化斜率,说明土层场地条件下,FP分量Tpk随Mw的变化速度快于FN分量的对应值。基岩场地条件下,FN和FP分量的Tpk基本相同;土层场地条件下,两分量Tpk在MW较小时差别不大,在MW较大时,FP分量的Tpk稍大于FN分量。当Mw相同时,两分量基岩场地上的Tpk均小于土层场地,说明基岩场地上的速度脉冲比土层场地更快达到其峰值。 图9 脉冲峰值时刻随断层距和震级的变化Fig.9 Variation of pulse peak time with fault distance and magnitude 图10 脉冲峰值时刻随震级变化的拟合结果及其对比Fig.10 Fitting result of variation of pulse peak time with magnitude and their comparison 与脉冲周期Tp的研究思路类似,本文将速度脉冲形状参数n分为峰值前形状参数n1和峰值后形状参数n2。观察图11发现,n1、n2随R和Mw的变化均没有明显的规律,这可能与每次地震不同的震源机制、传播途径和场地条件等因素有关。但本文在统计分析时发现,集集地震的形状参数n随着R的增大表现出增大的趋势,见图12。为了更直观地探究脉冲形状参数的空间分布特征,本文将集集地震近断层速度脉冲形状参数n1、n2在空间范围内的分布情况示于图13。 图11 脉冲形状参数随断层距和震级的变化Fig.11 Variation of pulse shape parameter with fault distance and magnitude 图12 集集地震脉冲形状参数随断层距的变化Fig.12 Variation of the pulse shape parameter of the Chi-Chi earthquake with fault distance 图13 集集地震脉冲形状参数分布图Fig.13 Distribution of pulse shape parameter of Chi-Chi earthquake 集集地震断层破裂方向大致为北偏东5°,脉冲型地震动记录主要分布在地表破裂断层附近,尤其在破裂断层前方区域较为集中,存在显著的方向性特征。形状参数在靠近破裂断层处与远离破裂断层处具有明显差异,较小的形状参数主要分布于靠近破裂断层区域,远离破裂断层处的脉冲形状参数更大,则连续半脉冲个数更多。同一水平分量的形状参数n1和n2在破裂断层北端区域表现出明显的差异,n2总体上大于n1;随着R的增大,FN和FP两分量脉冲形状参数的差异也随之增大。同一水平分量的形状参数n1和n2在缺少脉冲型地震记录区域存在差异,这可能与该区域脉冲型地震记录较少有关。鉴于目前无法通过多个地震事件得出脉冲形状参数的统计关系,建议先通过单个地震事件中脉冲形状参数的研究逐步揭示速度脉冲形状参数与震源机制以及震源破裂过程之间的关系。 表7 脉冲峰值时刻与震级的回归关系 基于PEER的NGA-West2强震数据库,选取126组近断层脉冲型地震动记录,采用李晓轩提出的速度脉冲模型拟合实际地震记录的FN和FP分量,提取出脉冲峰值Vp、脉冲周期Tp、脉冲峰值时刻Tpk、形状参数n等脉冲模型参数,分析震级Mw、断层距R、场地类别等对脉冲参数的影响,给出了若干速度脉冲特征参数的统计模型,并对比FN和FP分量脉冲参数之间的特性差异,通过分析得出以下结论: (1) FN分量Vp对Mw和R的敏感程度大于FP分量的相应值,基岩场地的Vp对Mw的敏感程度大于土层场地的对应值;场地土质越软,Vp受R的影响越小。 (2)Tp1、Tp2与Tp0均存在强线性相关性;FN分量Tp1随Mw的增大速率最大,Tp2随Mw的增大速率最小,Tp0随Mw的增大速率介于Tp1和Tp2之间;FP分量的Tp1和Tp0随Mw的增大速率差异不大,但均小于Tp2随Mw的增大速率;当Mw相同时,同一水平分量的Tp1和Tp2均大于Tp0。 (3) 在相同场地条件下,FN和FP分量的Tpk拟合值的差异较小;相较于基岩场地,土层场地上Tpk随Mw的变化速率的方向性差异更大;当Mw相同时,基岩场地上的速度脉冲比土层场地更快达到其峰值。 (4) 对于集集地震来说,较小的形状参数主要分布在靠近破裂断层处,远离破裂断层处的脉冲形状参数更大。在破裂断层北端区域,n2总体上大于n1;随着R的增大,FN和FP分量脉冲形状参数的差异也随之增大。 (5) 建议在进行近断层脉冲型地震动作用下结构响应分析时考虑地震动多分量输入以及速度脉冲特性差异的影响。 本文开展的脉冲参数提取及特性分析是以近断层脉冲型地震记录资料为依据的,其研究结果对近断层区域的结构抗震设计具有重要意义,同时为速度脉冲参数的确定提供了理论依据和计算方法。随着近断层脉冲型地震记录的逐渐增多,对速度脉冲特性的研究和认识必将更为深入,本文所采用的研究思路和方法可为脉冲参数化以及速度脉冲型地震动时程合成等方面的研究提供参考。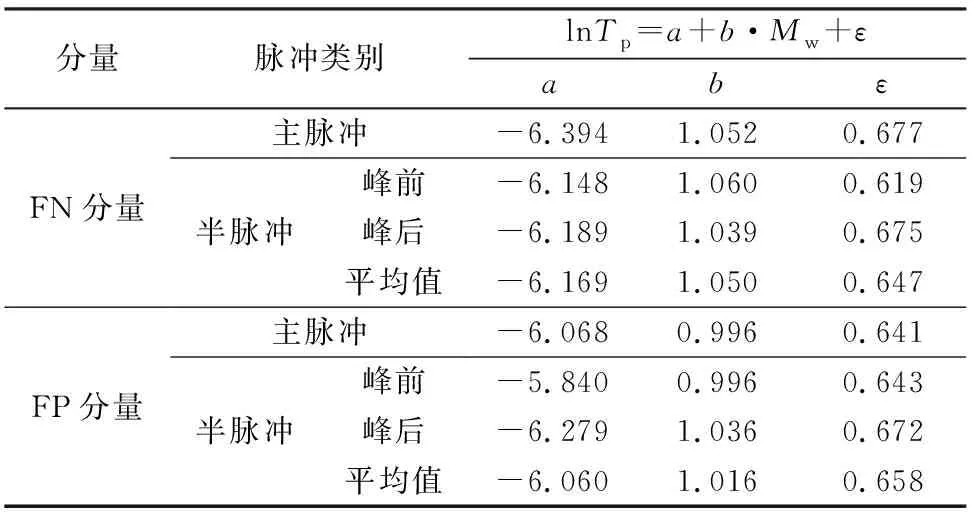
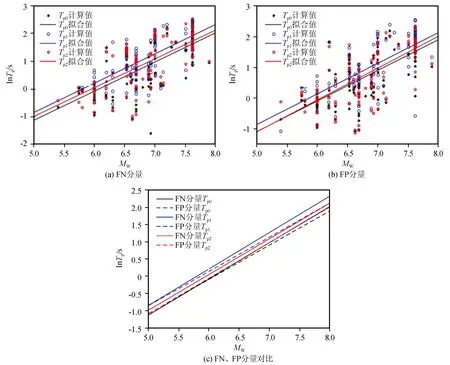
3.3 速度脉冲峰值时刻特性分析
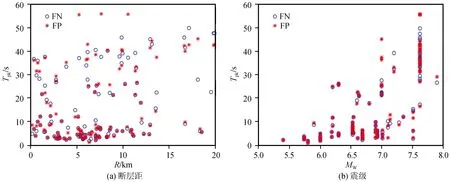
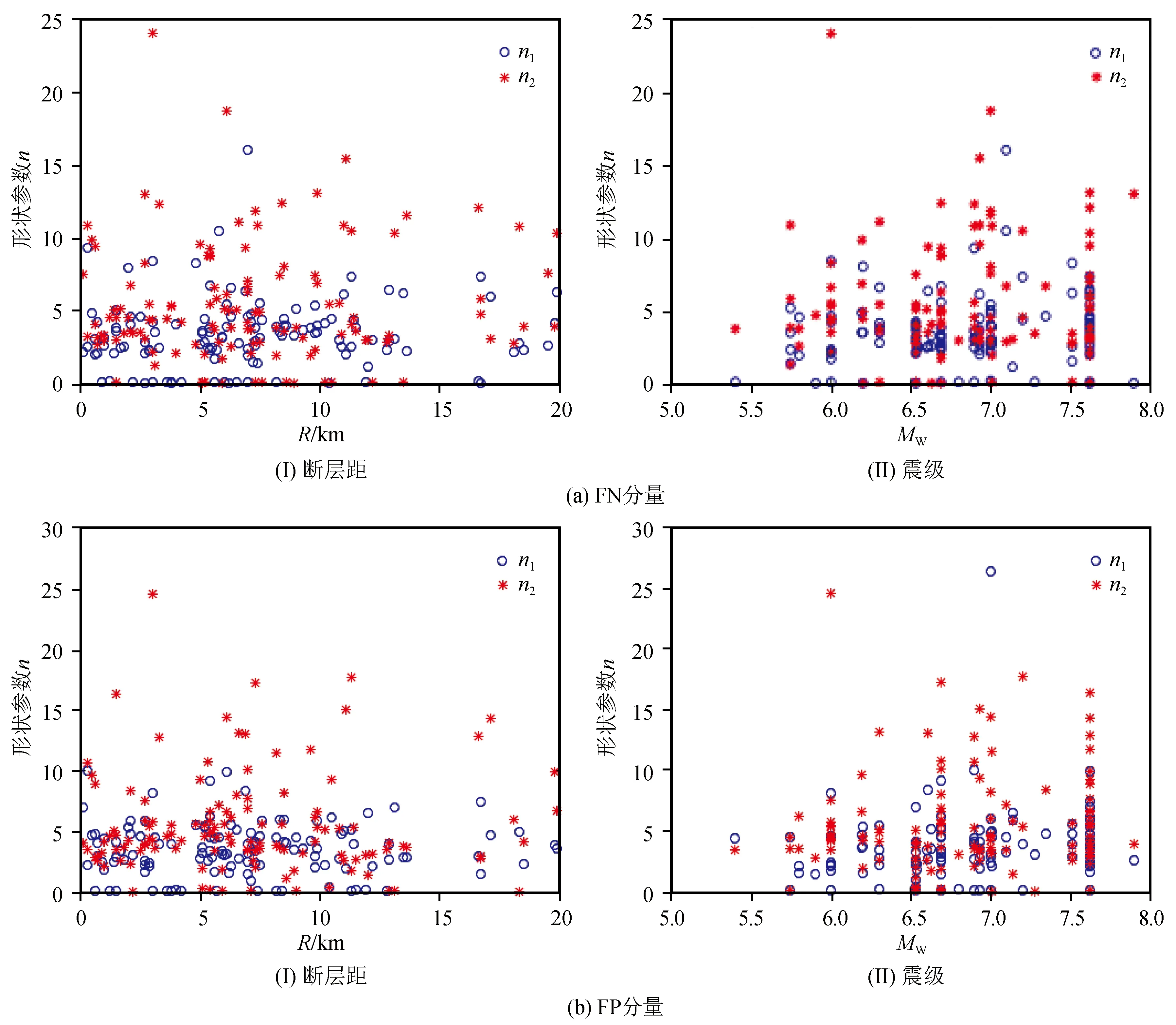
3.4 速度脉冲形状参数特性分析
4 结论与讨论
