基于芯样汉堡车辙试验的广西地区沥青路面车辙预测模型研究

林有贵， 杜荣耀

(1.广西高速公路养护工程技术研究中心，广西 南宁 530001；2.广西交投科技有限公司)

1 前言

现行JTG E20-2011《公路工程沥青及沥青混合料试验规程》以车辙试验的动稳定度作为评价混合料高温性能指标。在使用过程中曾出现室内动稳定度试验结果满足规范要求，但是现场实际路面车辙过深的情形。国内外众多研究结果表明：汉堡车辙试验作为一种评价沥青混合料高温抗车辙性能和水稳性能的试验方法，其评价结果与实际路用性能相关性高，可以确保二者之间的一致性。

各国规定的汉堡车辙试验评价标准各不相同。德国地方规范规定，荷载作用20 000次对应的汉堡车辙深度值应不大于4 mm；而美国AASHTO T324-2014规范仅指出了荷载作用的结束次数为20 000次，未对最大车辙深度作限制，而是要求各地区根据实际情况调整，但输出结果分析时却选取车辙深度20 mm作为其中的评价准则之一。由于美国国情的特殊性和各州环境气候的差异，如得克萨斯州、科罗拉多州、蒙大拿州等地区交通部门制定了适合本州实际情况的评价标准，其最大车辙深度值保持统一，荷载作用次数根据沥青等级调整。堪萨斯州和佛罗里达州则规定试验标准参照得克萨斯州的相关要求执行，而其余各州参照美国国家公路与运输协会标准AASHTO T324-2004或AASHTO T324-2014的规定执行。另外，有文献指出，在采用汉堡车辙试验评价混合料性能时，要求荷载作用20 000次对应的车辙深度值不大于20 mm。

在中国国内，崔文博等通过对典型车辙路面钻芯试样进行汉堡车辙试验，结果显示汉堡车辙试验结果和现场车辙深度显著相关，但是样本数较少，且文中并未指出路面集料的类型及强度；杜荣耀和林有贵指出钢轮会对强度较低的集料产生较严重压碎及磨耗，汉堡车辙试验不适用于评价粗集料压碎值大于20%的沥青混合料；中国国内其他汉堡车辙试验结果仅用于比对不同沥青混合料的抗车辙性能或研究汉堡车辙试验结果的影响因素，未建立室内试验结果与现场路面车辙关系，无法确定哪种沥青混合料的抗车辙性能符合要求。

张争奇等、张荷等曾在室内成型试件和现场取芯，加工成为类似于汉堡试件后进行动稳定度试验，建立了圆柱体芯样的动稳定度与板式试件动稳定度关系式；王辉和张肖宁采用现场芯样室内进行RWLT(旋转车辙仪)试验。但这些研究未将圆柱体动稳定度与现场车辙之间建立关系。显然，目前沥青混合料的高温性能评价还存在以下不足：评价高温性能的动稳定度试验与现场车辙相关性不够高，无法通过路面芯样动稳定度预测现场车辙深度；因此有必要研究汉堡车辙试验与现场车辙深度关系。该文对不同高速公路、不同车辙深度的路段钻取芯样，进行室内汉堡车辙试验，研究含有上、中面层混合料的双层复合试件的汉堡车辙分解方法，分别计算上中面层汉堡车辙变形，并据此建立以汉堡车辙试验值、区域车辙等效温度和累计标准轴次为变量的路面车辙预测模型。

2 调查路段状况及研究方案

2.1 调查路面状况

此次研究共选取广西地区7条运营高速公路、8个路段，其分布在桂南、桂中及桂北地区，基本涵盖了广西不同区域沥青路面状况。其中陡坡路段有南友路1段，坛百路1段，百罗路2段。7条高速公路的基本状况见表1。沥青面层厚15～18 cm，结构为“4+5+5”、4+5+6”或“4+6+8”形式，见表1。

表1 抽取的7条高速公路基本状况

2.2 研究方案

检测7条高速公路时，每条高速公路抽检不同坡度、不同车辙深度的沥青路面典型路段，现场量测车辙深度、纵坡度及钻芯取样。为使所取的芯样具有代表性，钻芯位置位于硬路肩靠近标线位置，该位置和行车道右轮迹带沥青混合料性质较为接近，能代表通车时的沥青混合料状况。同时分析典型路段的交通量、2013—2018年当地气象台的记录资料，并进行室内汉堡车辙试验，建立沥青路面现场车辙深度和汉堡车辙试验结果之间的关系，提出广西地区沥青路面车辙预测模型。

2.3 汉堡车辙试验条件

该文汉堡车辙试验在试验室进行，采用的试验仪器为美国生产的APA试验仪，可以进行汉堡车辙试验和APA车辙试验，平面钢轮直接加压于试件为汉堡车辙试验，采用凹面钢轮加压于橡胶管、而橡胶管置于试件表面即为APA试验。试验参数采用国际常用的标准，该文只进行汉堡车辙试验，具体试验指标如下：50 ℃恒温水浴；钢轮宽度47 mm，荷重158 LBS(磅)(1磅=0.454 kg)，轮压约0.7 MPa；加载速度：42次/min；试验终止条件：碾压次数达到20 000次或车辙深度达到12.5 mm时终止。每个试验持续8 h左右。

此次采用7条高速公路运营沥青路面在车辙处量测车辙深度，并钻芯量测上、中、下面层厚度，同时在应急车道紧临车辙处钻芯取样，与车辙处芯样对比得到各层的变形量，并取回路肩处芯样，切割为高度62 mm、加工为汉堡试样进行试验，保留全部上面层及部分中面层材料，见图1。

图1 汉堡车辙试验的双层复合试件(单位：mm)

3 交通量调查

对7条高速公路的交通量调查采用JTG D50-2017《公路沥青路面设计规范》中的交通参数分析方法：采集收费站出口车辆计重收费系统连续24 h不间断检测记录资料，得到汽车轴数和对应的每个轴重。其中，2轴车中只记录大客车、中型货车(如东风牌货车)等，不记录小客车、中巴等小型车辆，记录全部3轴及3轴以上车辆轴数及轴重。采用在最大车流量的位置同时设2台摄像机，24 h连续录像，记录全部上下行车辆，完成现场录像后在室内观看录像，按轴数和轴型统计交通量，计算车轴数对应轴型比例。采用运营公司统计的断面交通量、收费站出站客货车比例，计算断面日货车量。分析运营公司统计历年断面交通量，计算货车年增长率。

JTG D50-2017《公路沥青路面设计规范》采用轴载谱计算当量标准轴次，较为复杂，该文计算平均日当量轴次，进而计算累计标准轴次，车道系数取0.80，假设上、下行线交通量相等。应该指出，广西高速公路交通量不大但货车占比高、超载严重，计算得到的累计标准轴次大。例如百色至罗村口高速公路2019年半幅断面交通量仅1 587 pcu/d，但货车占比48%，而且超载严重。

4 现场车辙和室内汉堡车辙试验结果

4.1 现场检测结果

现场检测于2018年3—6月进行，7条路典型路段车辙深度、纵坡度、上中面层变形检测结果、汉堡车辙试验结果合并列于表2中。

表2 现场车辙检测和汉堡车辙试验及分析结果

续表2

4.2 室内汉堡车辙试验结果

汉堡车辙试件为2层不同材料的双层复合试件，高62 mm，见图1，其上层材料、厚度与路面的上面层完全相同，下层材料与路面中面层相同而厚度不同。由于广西高速公路上面层设计厚度一般为40 mm，因此汉堡试验复合试件上面层一般为40 mm左右，而下层厚度等于62 mm减去上面层厚度，一般为22 mm。由于施工厚度不可能精确控制，双层复合试件的上层厚度不可能恰好等于40 mm。现场检测结果、根据该文计算室内复合试件汉堡试验上、中面层变形以及汉堡总车辙深等一并列于表2。现场检测结果表明：路面的下面层变形极小，一般为0～2 mm，因此可认为路面表面总车辙仅由上中面层构成。

将表2中现场路表车辙值和复合试件汉堡试验车辙值关系绘于图2，由图2可见二者无显著相关，表明不能直接采用复合试件汉堡试验表面车辙值预测路面车辙。另外从表2可看出，大部分复合试件汉堡车辙总深很小，仅1.5～4 mm，无法直接量测上面层、中面层变形量，需按该文后述方法分解上、中面层变形，方能建立预测模型。

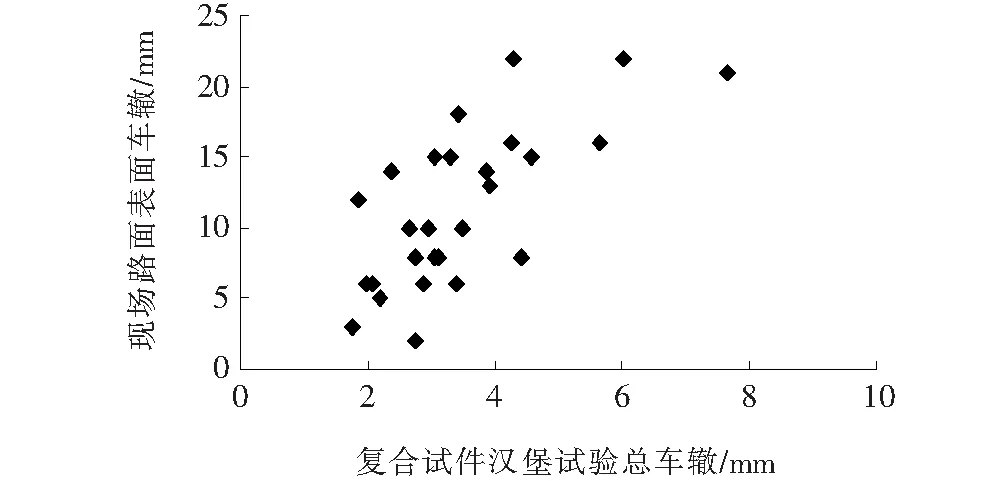
图2 现场路面车辙深度与复合试件汉堡试验总车辙关系

4.3 现场车辙及汉堡车辙关系

根据各路段现场车辙得到广西地区等效温度(表3)。由表3可得：纵坡度对沥青路面的抗车辙能力有较大的影响，当路面坡度大于3%，现场大纵坡处路面车辙明显大于相邻小纵坡段车辙，因此以下分析剔除纵坡大于3%的数据。按路段统计平均现场车辙、复合试件总车辙平均值、累计标准轴次列于表3。

表3 各路段现场车辙平均值和双层复合试件总车辙平均值

4.4 汉堡车辙试验结果分析

双层复合试件汉堡试验总变形等于上面层变形与中面层变形之和。从表2可见，复合试件上面层厚度在30～50 mm。汉堡车辙试验在50 ℃水中进行，可认为试件温度均匀。设图1的汉堡车辙试件的上、中面层厚分别为h1、h2x，显然h2x=62-h1。

鲁正兰和孙立军进行了不同温度、不同压力、不同厚度的车辙试验，回归得估算车辙深度式(1)：

(1)

式中:RD为车辙深度(mm)；T为沥青层温度(℃)；τ为车辆荷载作用下沥青层最大剪应力(MPa)；τ0为沥青混合料的抗剪强度(MPa)；ha为沥青层厚度(m)。

实际沥青路面服役过程中，路面的上面层和中面层的温度不相等，假设上下面层的温度分别为T1和T2。定义上面层的剪应力比σ1,T1为T1温度下的剪应力与T1温度下抗剪强度的比，中面层的剪应力比σ2,T2为T2温度下的剪应力与T2温度下的抗剪强度的比，即：

(2)

(3)

由式(1)、(2)和(3)得：

(4)

式中：RD1、RD2分别为路面现场上、中面层变形(mm)；h1、h2分别为上、中面层厚度(mm)。

汉堡试验在50 ℃水中进行，假设复合试件的汉堡车辙试验上、中面层变形分别为RH1、RH2，同时假定对于汉堡车辙试验式(1)仍成立，注意到T1=T2=50 ℃，由式(4)得：

(5)

式中：h2x意义见图1(mm)；σ1,50、σ2,50分别为在50 ℃条件下汉堡试验的上、中面层的剪应力比，由式(2)、(3)确定。

根据孙立军的分析，温度对沥青层剪应力影响微小，即可认为τ1,T1=τ1,50、τ2,T2=τ2,50；而抗剪强度随温度升高而降低，即[τ1,T1]<[τ2,T2]，又考虑到路面现场T1>T2,因此可近似认为下面等式成立：

(6)

简化得：

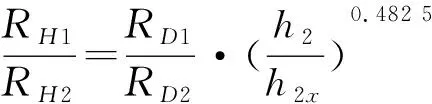
h2x=62-h1

(7)

此外，显然下式成立：

RH1+RH2=RH

(8)

式中：RH为复合试件汉堡车辙试验的总变形量(mm)。

根据式(7)、(8)可分别计算复合试件汉堡试验的上、中面层的变形量。

应该指出，双层复合试件下层(路面中面层混合料)厚度一般为22 mm左右，理论上不是完整的结构层。然而，在高速公路沥青路面养护实践中，曾铣刨上面层20 mm后加铺20 mm厚AC-8，例如自2015年以来坛百高速、南友高速、宜河高速等多条高速公路养护工程中，铣刨20 mm后(此时上面层剩余厚度20 mm)，然后加铺20 mm厚AC-8，这些路面至今已使用5年左右，使用效果良好，未出现结构性破坏，因此可认为复合试件的22 mm厚中面层材料特性与路面中面层相同。

标准汉堡车辙试验试件高为62 mm，表2的汉堡车辙试验试件为双层复合试件，上、中面层厚度并非62 mm，因此复合试件汉堡车辙试验结果应换算为厚度62 mm标准试件。根据式(1)，换算式如下：

(9)

(10)

式中：R62,1、R62,2分别为上、中面层混合料62 mm厚标准试件(单一混合料)汉堡车辙深度(mm)。

根据表2现场检测和室内汉堡试验结果、式(7)、(8)，可计算双层复合试件汉堡试验的上、中层变形，应用式(9)和(10)换算为62 mm汉堡试件单一混合料的变形，结果也列于表2。

4.5 汉堡试验车辙与现场车辙的关系

剔除表2中序号8、11和19共3个大纵坡路段数据后，上面层有27个数据；表2序号12～14为单层沥青层的复合式路面，无中面层，因此中面层有24个数据。 表4为相同路段的现场上中面层变形和相应的62 mm试件汉堡车辙的平均值。

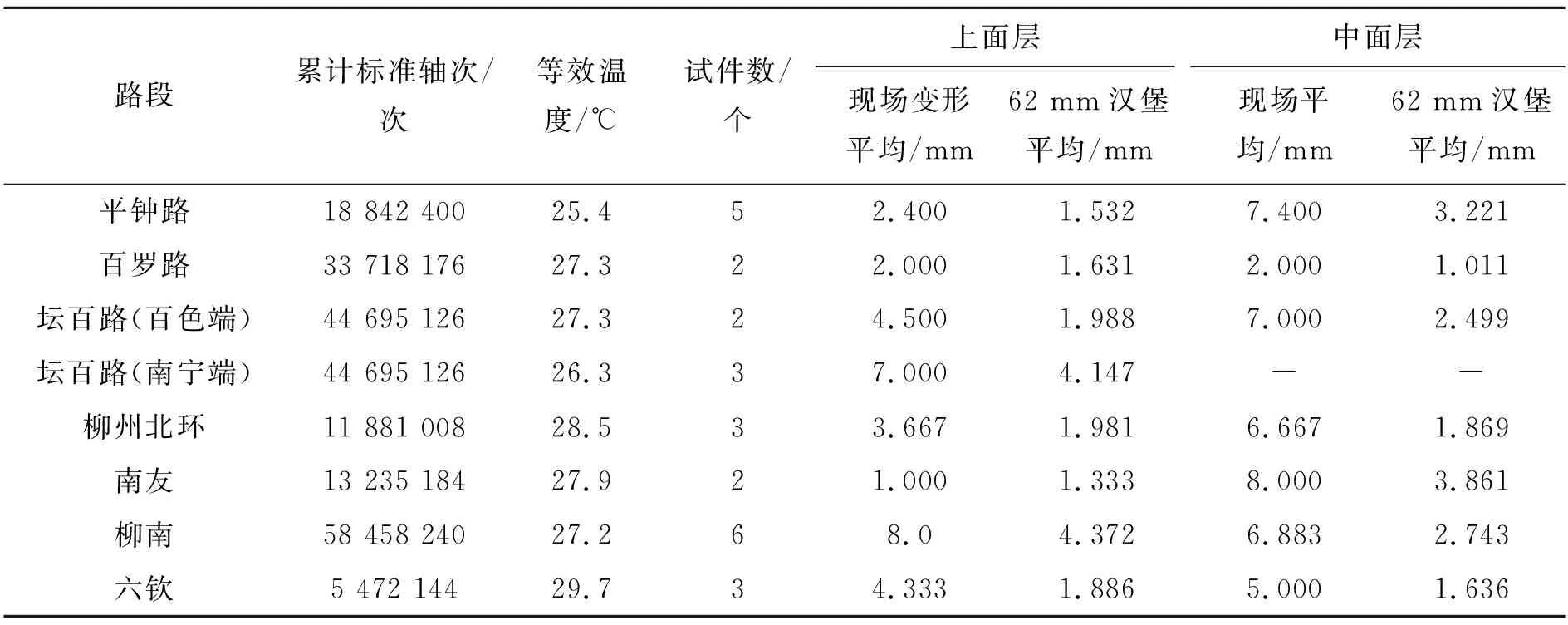
表4 8个路段现场变形和相应62 mm试件汉堡车辙平均值

JTG D50-2017《公路沥青路面设计规范》的预估路面车辙深度方程计入了累计标准轴次N和车辙等效温度T的影响，中国多个学者也曾通过室内动稳定度试验建立车辙RD与累计标准轴次、车辙等效温度的模型，均有如下形式：

RD=Af(σ,ha)TαNβ

(11)

式中：A为系数；α和β为常数；f(σ,ha)为与压应力σ(或剪应力)和沥青层厚度ha有关的函数。

现行规范和文献的预测模型中α和β值差异显著，其中α变化范围为0.748 2～3.758 6，β为0.370 4～0.835 8。考虑到现行规范车辙预测模型得到一定实践验证，而其余3个模型均源于室内试验拟合，因此，下面采用现行规范的α值(=2.93)，而变化β值，以期得到较佳拟合效果。

设定不同的β值，将表4的现场车辙变形采用式(12)作归一化处理：

(12)

式中：φTN定义为现场车辙因子；RD为上面层或中面层62 mm汉堡试验车辙。

理论上现场路面上中面层的车辙变形量与层厚有关，但此次检测路段上中面层厚度基本相同，即上面层设计厚度均为40 mm、中面层设计厚度为50 mm或60 mm，差异极小，因此现场车辙因子计算式(12)未考虑层厚因素。

分别对现场上、中面层变形进行归一化处理，并与室内62 mm汉堡车辙试验结果RH1、RH2作回归，得到的φTN1-RH1、φTN2-RH2关系及回归式见图3。图中y1=φTN1×105,y2=φTN2×105。当β取为0.12时，上、中面层的对数函数回归方程相关系数R2分别为0.936 1、0.856 8，复相关系数较大，拟合效果较好。系数β=0.12，表明交通量(累计标准轴次)对路面现场车辙影响较小，小于现行规范模型值。

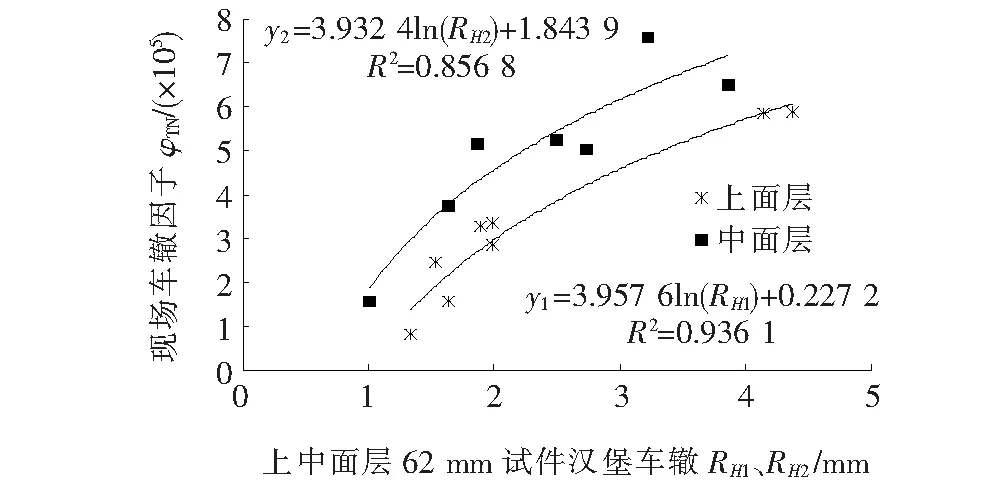
图3 上中面层现场车辙因子与相应汉堡车辙关系

根据图3和式(12)得到上、中面层现场车辙变形与室内62 mm试件汉堡车辙深度关系如下：

RD1=10-5×(3.957 6lnRH1+0.227 2)·T2.93·N0.12

(13)

RD2=10-5×(3.932 4lnRH2+1.843 9)·T2.93·N0.12

(14)

式中：RH1、RH2分别为路面现场上面层、中面层变形量(mm)；RD1、RD2为上、中面层材料62 mm试件汉堡试验车辙值(mm)；T为所在地区车辙等效温度(℃)，对于广西地区，区域车辙等效温度T按文献[20]取值，该值为分析广西2013—2018年6年气象资料提出来的。

4.6 路面车辙预测模型

将式(13)、(14)相加即得到式(15)所示的路面表面车辙深度预测模型：

RD=10-5×T2.93N0.12(3.957 6lnRH1+3.932 lnRH2+2.071 1)

(15)

根据路段所在区域的车辙等效温度T、考察年份的累计标准轴次N、沥青混合料配合比设计时62 mm厚试件的上、中面层混合料的汉堡车辙值RH1、RH2，或现场钻取芯样的汉堡车辙试验结果，按该文第4.4节提出的方法分别计算上、中面层变形值，根据式(15)可预测路面车辙深度随使用龄期(累计标准轴次)的变化。

5 结论

(1) 采用路面芯样切割成62 mm厚的含上、中面层材料的双层复合试件，汉堡试验的车辙需分解为上面层变形和中面层变形，这样处理后的各层变形方具有工程意义，而复合试件汉堡车辙总变形与实际路面表面车辙无显著相关关系。

(2) 该文采用现场实测上中面层变形、区域车辙等效温度和累计标准轴次确定车辙因子[式(12)]，以及该文提出的方法分别计算复合试件汉堡试验结果的上、中面层变形，建立了现场上中面层车辙因子与上中面层汉堡车辙变形的关系[式(13)、(14)]，相关系数R2分别为0.936 1、0.856 8，相关性显著，由此提出了式(15)的以上面层混合料、中面层混合料的62 mm厚试件的汉堡试验车辙值、累计标准轴次和车辙等效温度为变量的路面车辙预测方程。

(3) 车辙预测方程表明：交通量(累计标准轴次)对现场路面车辙影响量小于现行规范推荐值，即规范车辙预测模型的路面车辙深度与N0.48呈正比例关系，而该文研究结果为与N0.12呈正比例关系。