支吊架用卷边槽钢轴压构件的稳定性研究

吕蕴龙， 郭 兵

(山东建筑大学土木工程学院， 济南 250101)

0 引言

冷弯型钢品种繁多，截面形式多样[1]。支吊架用卷边槽钢是近些年新兴的一种单轴对称截面冷弯型钢，与普通卷边槽钢相比，多一个卷边，见图1。各种规格的支吊架用槽钢[2]仅截面高度h和壁厚t不同，截面宽度和卷边尺寸均为定值。当h较小时y轴为强轴，当h较大时x轴为强轴，与传统冷弯槽钢不同。

图1 卷边槽钢截面

国内外有关开口截面冷弯型钢轴压构件的研究资料很多，Yan J和 Young B[3-6]对复杂卷边固支轴压构件进行了试验及有限元研究，并提出了设计方法；王春刚等[7]采用直接强度法计算了斜卷边轴压构件稳定承载力；石宇等[8]基于试验及有限元分析结果提出一种针对冷弯薄壁卷边槽钢轴压构件的折减强度计算法；陈绍蕃[9]研究了卷边槽钢畸变屈曲与局部屈曲的相关性；何子奇等[10]通过试验研究了卷边槽钢轴压构件畸变与局部的相关屈曲；Schafer B W等[11]、王春刚等[12]发现，翼缘自由边采用多次弯折可以改善卷边槽钢的稳定性能。我国《冷弯薄壁型钢结构技术规范》(GB 50018—2002)[13](简称冷弯规范)中的柱子曲线只有一条，是根据轴压构件试验结合正则化长细比与构件截面类型回归出的等效初弯曲确定的，但构件截面形式中并未涉及到支吊架用卷边槽钢。《冷弯型钢结构技术标准》(GB/T 50018—2020)(报批稿)[14](简称冷弯标准报批稿)仍沿用上述方法。

残余应力是影响冷弯型钢整体稳定性能的一个重要因素。Wang C C等[15]通过电化学腐蚀切条法测量了冷弯薄壁C形钢的残余应力分布，发现冷弯构件的残余应力大多沿厚度线性分布，在弯折角处达到峰值；对于开口构件，内侧为压应力，外侧为拉应力；相同截面位置残余应力内外侧峰值十分接近。徐云志等[16]根据上述研究成果提出了一种残余应力的简化分布模型。

因目前暂未见到支吊架用卷边槽钢轴压构件的稳定研究资料，设计人员只能参照冷弯规范进行稳定设计，准确性尚未可知。本文采用ABAQUS有限元软件对支吊架用卷边槽钢轴压构件的稳定问题进行了数值分析，并根据分析结果提出了整体稳定系数计算方法。

1 有限元试件及模型验证

1.1 有限元试件设计

国内外规范对轴心受压构件整体稳定系数的定义基本是相同的，见式(1)；整体稳定系数与正则化长细比有关，见式(2)。

(1)

(2)

式中：φ为轴心受压整体稳定系数；Nu为极限承载力；Ny为截面屈服承载力，Ny=Afy，A为截面面积，fy为钢材屈服强度；λc为正则化长细比；λ为构件长细比；E为弹性模量。

由于支吊架用卷边槽钢截面积小且初弯曲、初偏心、残余应力等多种因素相互交织，使得这类构件的稳定问题较为复杂，设计试件时需充分考虑。根据我国现行《装配式支吊架系统应用技术规程》(T/CECS 731—2020)[2]推荐的常用卷边槽钢截面尺寸，共设计了三大系列有限元试件，见表1，其中B系列按壁厚t不同又分为B1，B2和B3三个子系列。A，B系列的强轴为y轴，C系列的强轴为x轴。因影响整体稳定系数的主要因素是长细比，每个系列试件共设计了八种长细比，所涵盖的正则化长细比λc范围为0～1.8。全部试件均采用两端铰接约束，材料为Q235钢。

有限元试件参数 表1

影响轴压构件稳定性的初始缺陷有初弯曲、初偏心和残余应力。初弯曲、初偏心对轴压构件的稳定影响在本质上相同，且影响程度接近，二者以最大值同时出现在同一构件的概率较低，故冷弯规范采用适当放大的初弯曲统一考虑。为研究初弯曲对卷边槽钢轴压稳定承载力的影响，表1中每个系列每种长细比均设一个标准缺陷试件及两个对比缺陷试件，共120个。标准缺陷试件的初弯曲挠度取l0/1 000(l0为构件几何长度)，对比缺陷试件的初弯曲挠度分别取l0/2 000，l0/500。

因支吊架用卷边槽钢属于新型截面，有关其残余应力的研究暂未见于文献，本文采用文献[15]的方法推导了其截面残余应力分布，见图2。卷边槽钢截面残余应力沿壁厚呈线性分布，压应力为正，拉应力为负。弯折处残余应力峰值系数β1取0.4，影响范围取1.5t；其余位置的峰值系数β2取0.2。试件的初弯曲与残余应力不予同时考虑，表1中每个系列每种长细比均设一个无残余应力试件和一个有残余应力试件，共80个。考虑以上所有参数，本文共设计有限元试件200个。

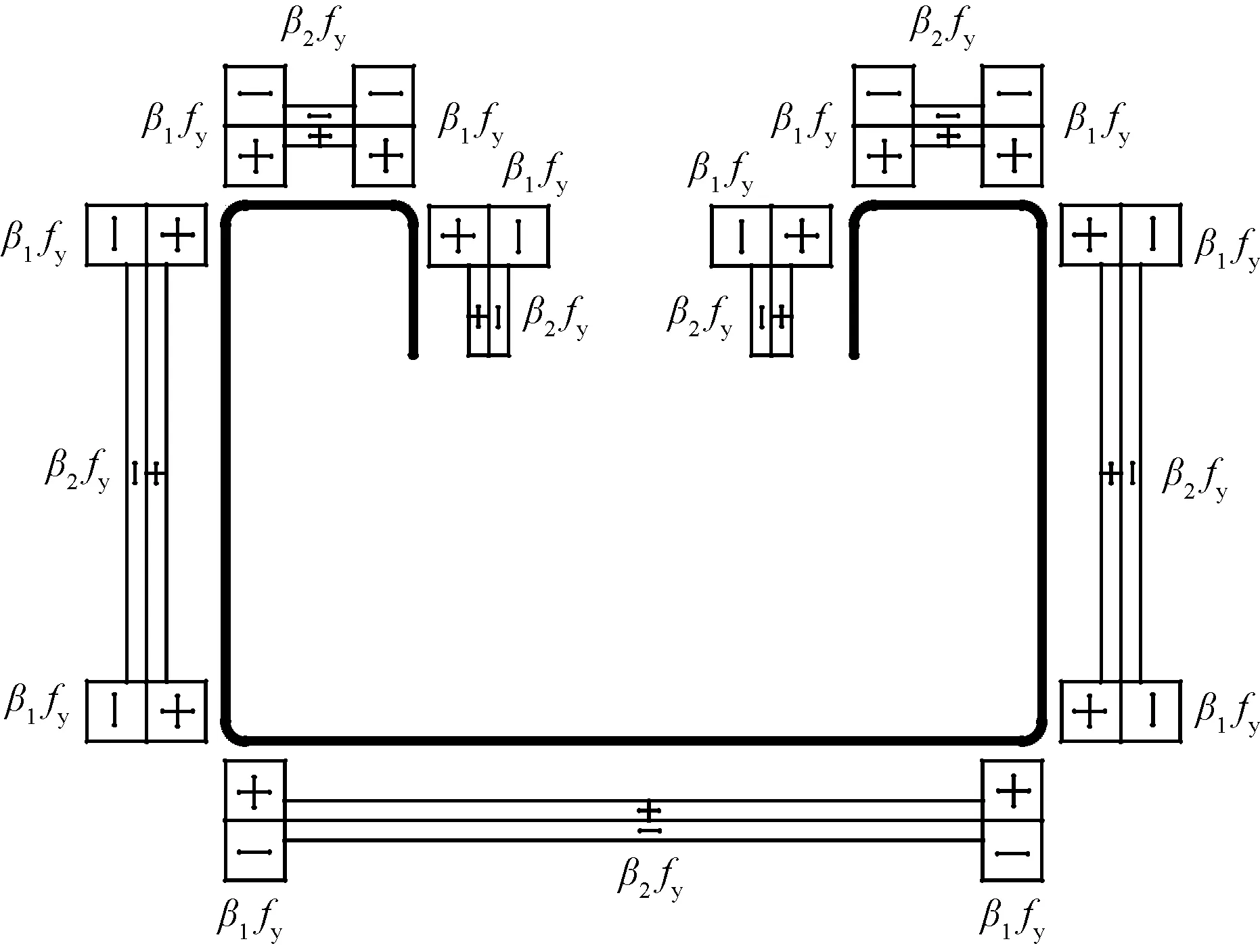
图2 卷边槽钢残余应力

1.2 有限元模型及验证

有限元模型采用C3D20实体单元，试件的边界条件为两端铰接，通过构件端部的耦合点施加约束，荷载位于截面形心，位移加载。材料采用理想弹塑性模型，屈服强度fy=235MPa、弹性模量E=206 000MPa、泊松比υ=0.3。

初弯曲通过更新单元节点初始坐标的方法完成。先使用Lanczos法进行弹性屈曲分析并得到一阶屈曲模态的节点坐标值，再根据初弯曲值将一阶屈曲模态坐标值乘以一定比例系数输入到模型中，最后通过Risk分析对已施加初弯曲的模型进行大变形非线性分析，得到试件稳定承载力。

残余应力通过在初始分析步中设置预定义场的方式施加，先根据残余应力分布位置将试件划分为不同的区域，再将截面中不同残余应力的单元划分到不同的集合中并分别施加相应的残余应力值。

因没有支吊架用卷边槽钢轴压构件的试验研究资料，为验证上述方法的可靠性，对文献[12]中的16个复杂卷边槽钢轴压试件进行了分析，试验结果与有限元结果的对比情况见表2。试件编号与文献[12]相同，表中L代表局部屈曲，D代表畸变屈曲。从表2可以看出，承载力平均相差4.3%，最大相差6.8%，失稳类型完全一致，说明本文有限元方法是可靠的，且精度较高。

试验结果与有限元结果的对比对比 表2

2 有限元参数分析

2.1 截面尺寸的影响

A，B，C系列所有试件除截面尺寸和长细比不同外，初弯曲均采用l0/1 000，无残余应力。分析结果表明，所有试件均为整体失稳，未发生局部屈曲和畸变屈曲。试件整体失稳类型与截面高度有关，A系列试件的截面高度是截面宽度的1/2，绕x轴的抗弯刚度EIx远小于绕y轴的抗弯刚度EIy，因此试件绕非对称轴x轴发生弯曲屈曲，如图3(a)所示。B系列试件的截面高度与截面宽度相等，EIx与EIy同量级，C系列试件截面高度大于截面宽度，EIx大于EIy，B，C系列试件均绕对称轴y轴发生弯扭屈曲，如图3(b)所示。上述情况说明，支吊架用卷边槽钢轴压构件的失稳形式与截面高度有关，当截面高度大于或等于41.3mm时，将发生弯扭屈曲。

图3 试件整体失稳类型

A，B2及C系列试件的截面高度不同，其余参数均相同，截面高度对柱子曲线的影响见图4。可以看出，截面高度变化对整体稳定系数略有影响，主要是由于失稳形式不同而引起的。当λc≥0.5时，A系列试件(弯曲屈曲)的柱子曲线位于B2和C系列试件(弯扭屈曲)的下方，但差距较小，可忽略。

图4 截面高度对柱子曲线的影响

B1，B2，B3系列试件仅壁厚不同，其余参数相同，壁厚对柱子曲线的影响见图5。可以看出，三条曲线基本重合，说明壁厚对整体稳定性能的影响也可忽略。

图5 壁厚对柱子曲线的影响

2.2 初弯曲的影响

考虑不同程度初弯曲后的A，B，C系列试件计算结果见图6～8，图中α0，α1，α2分别表示考虑的初弯曲挠度为l0/1 000，l0/2 000，l0/500。

从图6～8中可以看出：1)初弯曲对各系列试件的整体稳定系数均有明显降低作用，初弯曲越大，影响越显著；2)当初弯曲为定值时，降低程度与λc有关，λc=1.0时降低幅度最大，为11%；3)不同截面尺寸试件在相同长细比下对初弯曲的敏感度几乎相同，说明初弯曲对整体稳定系数的影响与失稳类型无关。

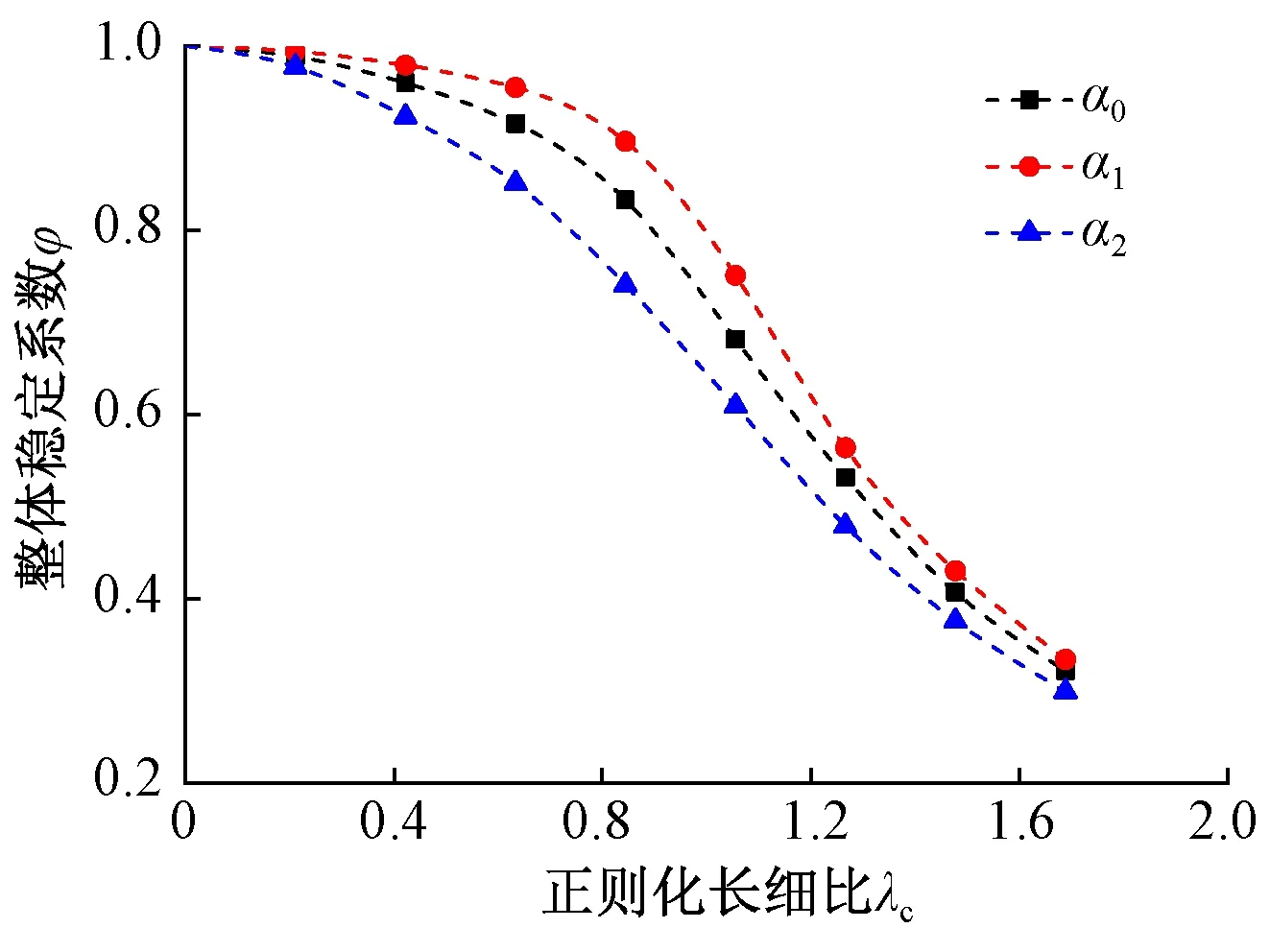
图6 初弯曲对A系列试件的影响

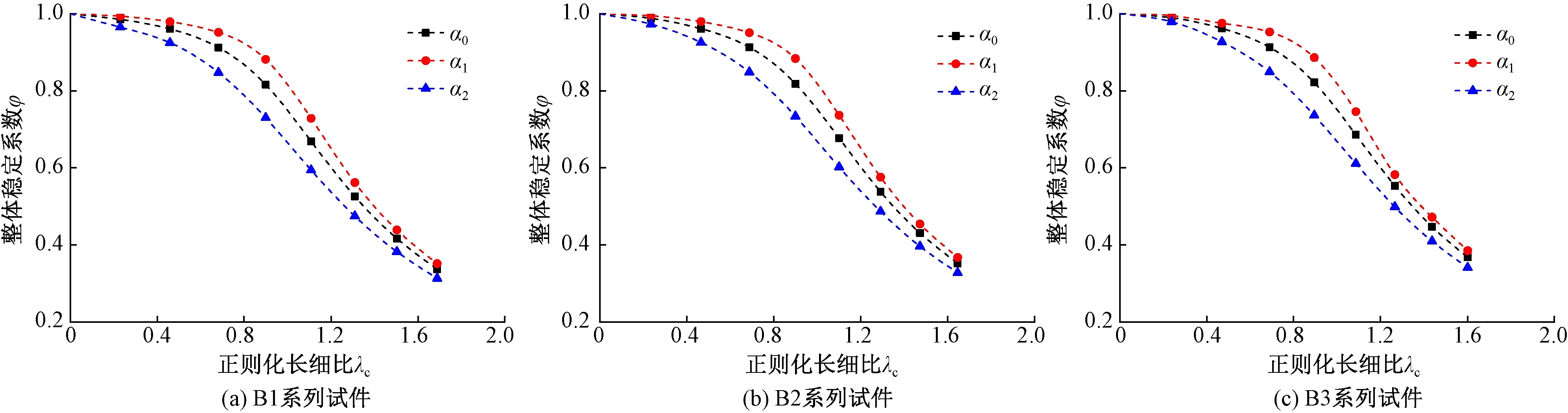
图7 初弯曲对B系列试件的影响

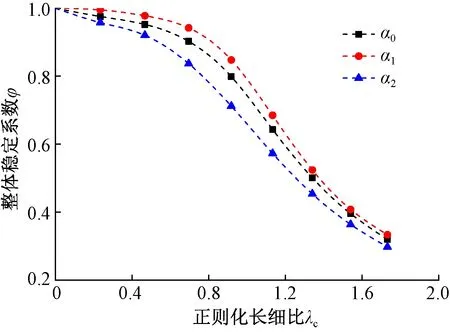
图8 初弯曲对C系列试件的影响

2.3 残余应力的影响

A，B，C系列试件的计算结果见图9，图中纵坐标为有残余应力时稳定承载力Pb1与无残余应力时稳定承载力Pb0的比值。可以看出，残余应力对稳定承载力有降低作用，降低程度与正则化长细比有关，当λc=0.9时降低幅度最大，仅为8%，说明残余应力的影响并不显著，主要是由于冷弯型钢的残余压应力峰值低。

从图9还可以看出，残余应力对稳定承载力的影响与截面高度无关，但与壁厚有关，壁厚大时影响也大。这是因为当壁厚增大时，弯折角处峰值残余应力影响范围增大。

图9 残余应力的影响

3 整体稳定系数计算方法

国内外规范提供的柱子曲线都是用放大的初弯曲来统一考虑诸参数影响的，为考虑残余应力等参数对试件整体稳定的不利影响，初弯曲可采用冷弯标准报批稿建议的l0/500。

3.1 有限元分析结果与我国冷弯标准报批稿的对比

冷弯标准报批稿中关于轴压构件稳定系数的表达式如式(3)所示，其中ε0为相对初弯曲。由此可知稳定系数与构件的正则化长细比和相对初弯曲有关。ε0的大小与构件自身的截面形式有关，对于不同的截面形式，ε0的取值有较大不同。为了综合考虑各方面的影响，规范采用等效相对初弯曲εe0来替代ε0，通过对方钢管、槽钢、角钢等常用的164个截面形式不同的轴压构件进行试验，回归出了εe0的取值方法，式(4)为回归后εe0的表达式。

(3)

(4)

本文计算的柱子曲线与冷弯标准报批稿柱子曲线对比见图10，可以看出，本文柱子曲线高于冷弯标准报批稿柱子曲线，平均偏高7%，最大偏高10%。出现这种情况的原因是规范中柱子曲线只有一条，为尽可能涵盖各类截面并确保可靠度，曲线取值偏低，各类文献的试验结果大多位于规范曲线上方也证明了这一点。因此，按照冷弯标准报批稿柱子曲线进行支吊架用卷边槽钢轴心受压构件的设计是偏于安全的。

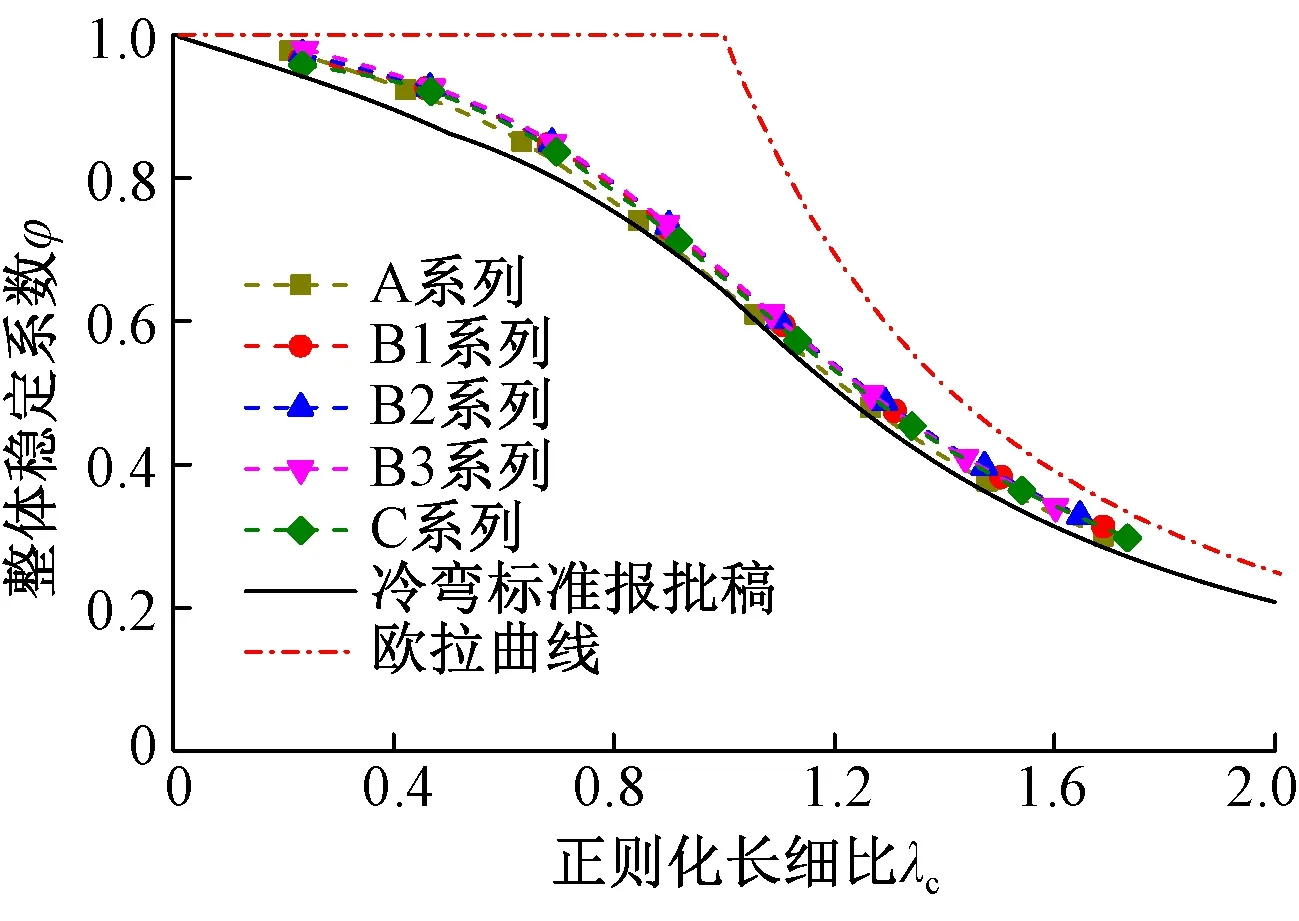
图10 有限元分析结果与我国冷弯标准报批稿柱子曲线的对比

3.2 有限元分析结果与美国规范的对比

美国AISI S100-16规范[17](简称AISI规范)中根据长细比不同采用分段式的方法计算轴心受压构件的稳定承载力，公式如下：

(5)

(6)

式中：Fy为屈服应力；Fn为极限压应力；Fcre为弹性屈曲临界应力。

将式(5)代入式(1)，可以得到整体稳定系数φ与正则化长细比λc的关系：

(7)

本文柱子曲线与美国AISI规范柱子曲线对比见图11。当λc<1.0时，本文柱子曲线位于AISI规范柱子曲线的上方；当λc>1.0时，本文柱子曲线位于AISI规范柱子曲线的下方，但偏差均较小。

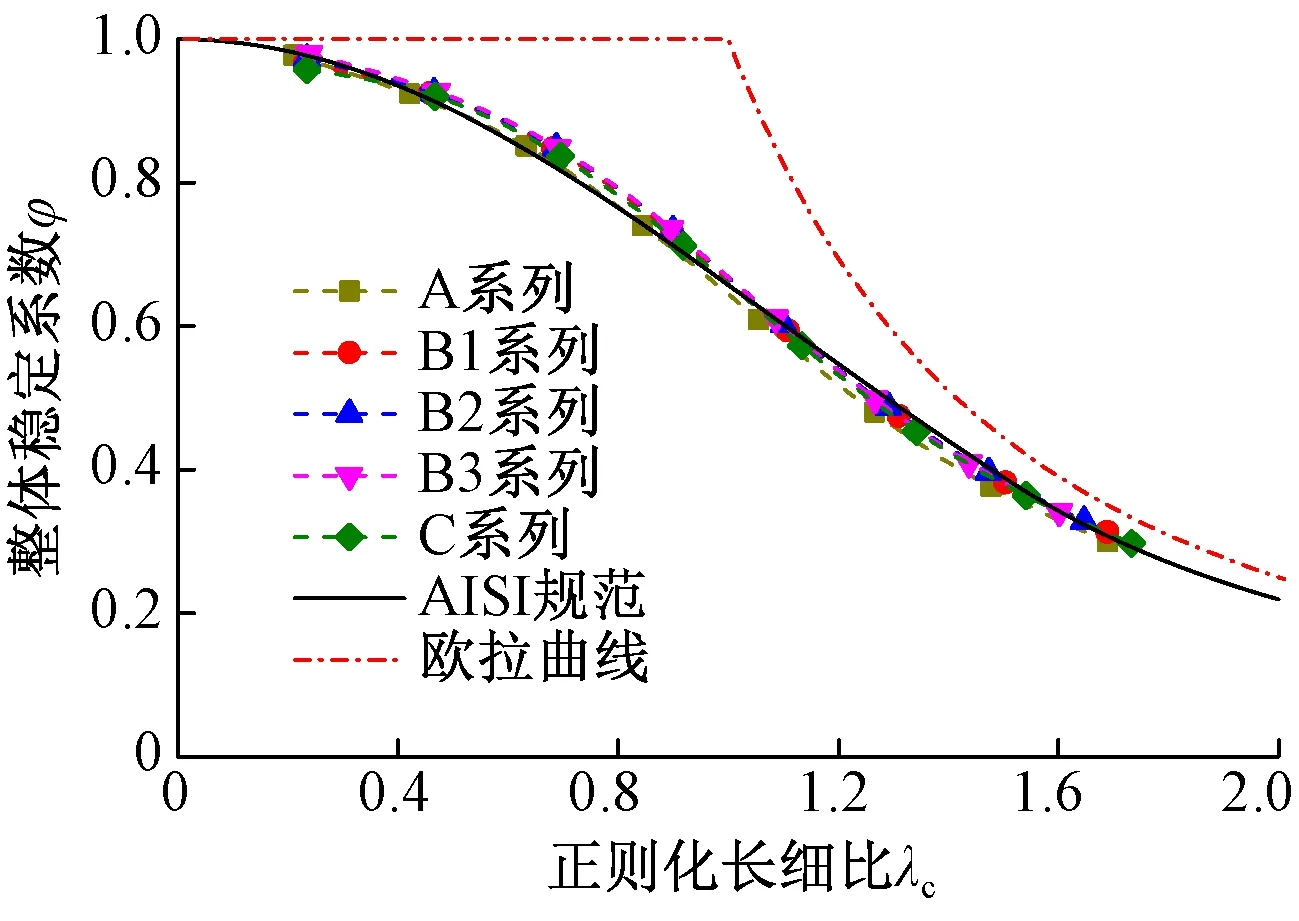
图11 有限元分析结果与美国AISI规范柱子曲线的对比

3.3 整体稳定系数的计算方法

从图10已知，支吊架用卷边槽钢采用冷弯标准报批稿推荐的柱子曲线进行稳定设计是偏安全的。为了便于精细化设计，应给出这类截面柱子曲线计算方法。

考虑到冷弯标准报批稿柱子曲线与《钢结构设计标准》(GB 50017—2017)[18](简称钢结构标准)中的b类曲线较为接近，借鉴钢结构标准中柱子曲线的计算方法，根据本文数值分析结果作为该构件整体稳定系数的设计依据，拟合出稳定系数表达式，见式(8)。

(8)

式中b1，b2，b3为参数。

对于支吊架用卷边槽钢，尽管不同规格槽钢的强弱轴及失稳类型不同，但整体稳定系数相差并不大，均在5%以内，故此类试件可采用同一条柱子曲线表示。经拟合，参数b1=0.620，b2=0.988，b3=0.190。图12为式(8)计算拟合后的柱子曲线与有限元分析结果对比，两者吻合程度较高，离散性均小于2%，可见式(8)可用于支吊架用卷边槽钢轴心受压构件的整体稳定计算。

图12 有限元分析结果与拟合柱子曲线对比

4 结论

本文采用有限元方法对支吊架用卷边槽钢轴心受压构件的稳定性进行了研究，考虑了截面尺寸、初弯曲和残余应力的影响，初步得到如下结论：

(1)《装配式支吊架系统应用技术规程》(T/CECS 731—2020)推荐的冷弯槽钢截面轴心受压时不会发生局部屈曲和畸变屈曲，只能发生整体失稳。

(2)壁厚对整体稳定系数无影响，但截面高度的变化会影响构件的失稳形式，截面高度小于41.3mm时为弯曲屈曲，截面高度大于或等于41.3mm时为弯扭屈曲。

(3)初弯曲对整体稳定系数有明显降低作用，影响程度与初弯曲值和试件的正则化长细比有关，与失稳类型无关，正则化长细比为1.0时影响幅度最大。

(4)残余应力对整体稳定系数也有降低作用，但影响程度较小，与壁厚、正则化长细比有关。

(5)按照冷弯标准报批稿中的柱子曲线进行稳定设计是偏于安全的，整体稳定系数也可按式(8)计算。