部分包覆钢-混凝土组合柱单向压弯承载力计算方法比较*
2021-05-13陈以一
王 海, 李 杰, 陈以一,3
(1 上海市政工程设计研究总院(集团)有限公司, 上海 200092; 2 同济大学土木工程学院, 上海 200092; 3 上海杉达学院, 上海 201209)
0 引言
部分包覆钢-混凝土组合构件(Partially-Encased Composite Steel and Concrete Member,简称PEC构件)是混凝土部分包覆H形或双H形钢骨(称主钢件)而形成的一种组合构件。典型的截面形式见图1。主钢件通常有两种,即厚实型的热轧型钢和薄柔型的焊接组合截面。PEC构件的显著优点是防止腹板局部失稳,避免或延缓受压翼缘屈曲,改善钢构件防火,适合预制装配。由于其兼具钢结构快速装配和混凝土结构防火防腐、隔声隔振好的优点,因此非常适合住宅、办公楼建筑。此外,在既有钢结构厂房性能提升设计中不失为一种加固良策。
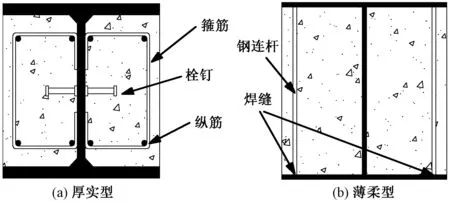
图1 PEC柱截面类型
现阶段,针对PEC柱的受力性能,国内外学者进行了大量研究。
Elnashai等[1]对分别配置有纵筋、箍筋、钢连杆的厚实型截面PEC柱进行了不同轴压比下的循环加载和伪动力试验研究;Tremblay等[2-3]对薄柔型截面PEC柱进行轴压试验研究,提出了考虑翼缘局部屈曲及钢板残余应力的轴压承载力计算公式;Bouchereau等[4]进行了PEC柱的轴压和压弯试验研究;Prickett等[5]对高性能混凝土PEC柱进行了轴压和偏压试验研究。
赵根田等开展了PEC短柱的轴压[6]、单向偏压[7]、抗震性能[8]试验研究;朱晓娟[9]进行了PEC短柱的双向偏压试验;陈以一等[10]对受恒定轴压力和水平往复荷载的PEC柱进行试验研究和数值分析;方有珍等[11-12]进行了薄柔型截面PEC柱绕强轴和弱轴的滞回性能试验研究;宋宇宸等[13]利用数值分析手段对PEC柱钢翼缘的局部屈曲和屈曲后行为进行研究;简思敏[14]对采用再生混合混凝土PEC柱的轴压和偏压受力性能进行试验研究和有限元分析。林德慧等[15]对PEC柱的轴压和压弯整体稳定承载力进行数值分析。
对于PEC柱的设计,目前国内最重要的标准有《部分包覆钢-混凝土组合结构技术规程》(T/CECS 719—2020)[16](简称《PEC规程》),另外可以参照的标准有《组合结构设计规范》(JGJ 138—2016)[17](简称《组规》)、《矩形钢管混凝土结构技术规程》(CECS 159∶2004)[18](简称《矩形钢规》)。欧洲规范EN 1994-1-1[19]对厚实型PEC构件有详细设计规定;加拿大规范CSA-S16-09[20]对薄柔型PEC压弯构件也有具体设计方法。但上述规范在PEC柱压弯设计方法之间的区别尚无系统研究,各规范计算值和试验结果的差异等尚无对比研究。鉴于此,本文对上述问题展开研究,探究各规范在PEC柱单向压弯承载力计算上的差异。
1 单向压弯承载力理论计算方法
1.1 规范EN 1994-1-1
轴压强度计算时,假定主钢件全截面塑性,受压混凝土应力矩形分布,混凝土的强度乘以0.85的折减系数,钢筋屈服,截面塑性抗压承载力设计值Npl,Rd为:
Npl,Rd=Aafyd+0.85Acfcd+Asfsd
(1)
式中:Aa,Ac,As分别为主钢件、混凝土和纵筋的截面面积;fyd,fcd,fsd分别为钢材屈服强度、混凝土圆柱体抗压强度和纵筋屈服强度设计值。
应满足轴力设计值NEd≤χNpl,Rd,其中屈曲折减系数χ:
(2)
(3)
(4)
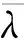
弹性临界力Ncr:
(5)
(EI)eff=EaIa+EsIs+KeEcmIc
(6)
Ecm=22×[0.1×(fck+8)]0.3
(7)
式中:(EI)eff为有效抗弯刚度特征值;l0为柱的计算长度;Ia,Is,Ic分别为主钢件、纵筋、未开裂混凝土截面的惯性矩;Ea,Es分别为主钢件、纵筋的弹性模量;fck为混凝土圆柱体28d抗压强度特征值;Ecm为混凝土的弹性割线模量;Ke为混凝土的校正系数,Ke=0.6。
抗弯计算时,假定主钢件全截面塑性,混凝土受压应力取0.85fcd并按矩形分布,受拉和受压钢筋屈服,求得截面塑性抗弯承载力Mpl,Rd。
单向压弯计算时,柱端弯矩和考虑构件缺陷及二阶效应后的柱中最大弯矩两者中的较大值MEd应满足:
MEd/Mpl,N,Rd=MEd/(μdMpl,Rd)≤αM
(8)
k=β/(1-NEd/Ncr,eff)
(9)
(10)
(EI)eff,Ⅱ=K0(EaIa+EsIs+Kc,ⅡEcmIc)
(11)
式中:αM取0.8或0.9;Mpl,N,Rd为与轴力NEd对应的截面塑性抗弯承载力;k为弯矩二阶效应放大系数;β为等效弯矩系数,对等偏心距加载的单曲率弯曲的情况取1.1;Ncr,eff为欧拉弹性临界力;(EI)eff,Ⅱ为有效抗弯刚度设计值;Kc,Ⅱ取0.5;K0取0.9。构件的初始缺陷:对强轴压弯取构件长度的1/200,对弱轴压弯取构件长度的1/150。
1.2 规范CSA-S16-09
加拿大规范CSA-S16-09给出PEC柱的压弯承载力计算方法,采用轴力-弯矩线性相关公式:
Cf/Crc+Mf/Mrc≤1
(12)
Crc=(φAseFy+0.95α1φcAcfc′+φrArFyr)(1+λ2n)-1/n
(13)
式中:Crc为考虑翼缘受压屈曲的轴压承载力;n=1.34,φ=0.9,φc=0.65,φr=0.85;Fy,fc′和Fyr分别为钢材的屈服强度、混凝土28d抗压强度和钢筋的屈服强度标准值;Ac,Ar分别为混凝土和纵筋截面面积;Ase为主钢件有效截面面积。
Ase=(d-2t+2be)t
(14)
(15)
(16)
k=0.9/(s/bf)2+0.2(s/bf)2+0.75
(17)
λ=(Cp/Cec)0.5
(18)
Cec=π2EIe/(KL)2
(19)
EIe=EaIa+EsIs+0.6EcIc/(1+Cfs/Cf)
(20)
式中:be为翼缘有效宽度;λp为无量纲的翼缘宽厚比;Cec为组合柱的欧拉屈曲临界力;以φ=φc=φr=1,λ=0代入式(13)求得组合柱的名义抗压承载力Cp;K为有效长度系数;EIe为等效抗弯刚度;Cf为柱子总轴力;Cfs为柱子长期荷载作用下的轴力;L,d,bf,s分别为柱几何长度、柱截面总高度、截面宽度和连杆间距;t为腹板/翼缘厚度。
Mrc=Cre+Cr′e′
(21)
Cr=0.5(φAsFy-Cr′)
(22)
Cr+Cr′=φAstFy
(23)
Cr′=1.18α1φca(b-t)fc′
(24)
式中:Mrc为截面抗弯承载力;Cr,e分别为全截面受压主钢件合力以及该合力点到受拉主钢件合力点的距离;Cr′,e′分别为受压区混凝土合力(绕强轴)以及该合力点到受拉主钢件合力点的距离;a为混凝土受压区的高度;As为主钢件的截面面积;b可以用bf替代,都指翼缘的宽度;Ast为受拉主钢件的截面面积。
1.3 《PEC规程》
单向压弯PEC柱平面内稳定承载力按:
N/φxNu+βmxMx/Mux(1-φxN/NEx)≤1
(25)
(26)
(EI)e=EaIa+EsIs+keEcIc
(27)
(28)
式中:φx为轴心受压构件绕强轴x轴的整体稳定系数,按《钢结构设计标准》(GB 50017—2017)(简称《钢标》)附录A选取,对x轴取b曲线,对弱轴y轴取c曲线;NEx为轴心受压构件绕x轴的弹性稳定临界力;l0为轴心受压构件的计算长度;(EI)e为构件等效抗弯刚度;ke为折减系数,取0.5;βmx为等效弯矩系数,按《钢标》计算;Nu为截面受压承载力;fa′,fc,fy′分别为主钢件抗压强度设计值、混凝土轴心抗压强度设计值、钢筋抗压强度设计值;Aa,Ac,As分别为主钢件、混凝土、纵筋的截面面积;N为轴力设计值;Mux为截面受弯承载力,受压区混凝土按等效矩形应力分布,并达到轴心抗压强度,受拉区混凝土的作用不予考虑,截面钢材均达到各自抗拉、抗压强度设计值,纵筋受拉或受压达到屈服强度。
1.4 《组规》
《组规》依据混凝土构件设计方法,将矩形钢管混凝土偏压柱分成大偏心受压和小偏心受压。大偏心受压时,截面应力分布为:忽略受拉区混凝土作用,混凝土受压区按矩形应力块,高度x,应力大小为α1fc;钢截面应力按全塑性分布,应力大小为fa,中和轴高度为x/β1。小偏心受压时,截面应力分布为:混凝土部分同大偏心受压;钢截面应力按矩形分布,但应力σa达不到屈服强度,取值按σa=fa(x/hc-β1)/(ξb-β1)。由于构件长细比和偏心带来的附加弯矩的影响,可通过式M=CmηnsM2考虑,且要计入附加偏心距ea。将上述方法应用于PEC柱偏压计算,计入受拉钢筋和受压钢筋的作用,采用截面极限平衡法可建立PEC柱偏压承载力计算公式。
1.5 《矩形钢规》
对于单向压弯的矩形钢管混凝土柱,《矩形钢规》弯矩作用平面内的稳定承载力公式为:
N/(φxNu)+(1-αc)βMx/[(1-0.8N/NEx′)Mux]≤1
(29)
且应满足
βMx/(1-0.8N/NEx′)Mux≤1
(30)
Nu=faAa+fcAc
(31)
Mux=fa0.5Aa(h-2t-dn)+bt(t+dn)
(32)
αc=fcAc/(faAa+fcAc)
(33)
NEx′=NEx/1.1
(34)
(35)
式中:Nu为构件的轴压承载力;Mux为构件的抗弯承载力;αc为混凝土工作承担系数;φx为绕x轴(平面内)的轴心受压稳定系数;dn为混凝土受压区高度;h,b分别为组合截面高度、宽度;t为主钢件壁厚;NEx为欧拉临界力;λx为长细比;β为等效弯矩系数。将上述方法应用于PEC柱偏压计算,计入受拉钢筋和受压钢筋的作用,得到类似的在弯矩作用平面内的稳定承载力计算公式。
2 理论计算结果与试验数据的比较
以上述五种方法分别计算得到单向偏压PEC柱截面的N-M(轴力-柱端弯矩)相关曲线,与轴力-柱端弯矩试验点(图中用空心点示意)比较如图2~4所示。试验中PEC柱的长高比L/d均为5,主要参数见表1、表2,其他参数详见文献[4-5,14]。
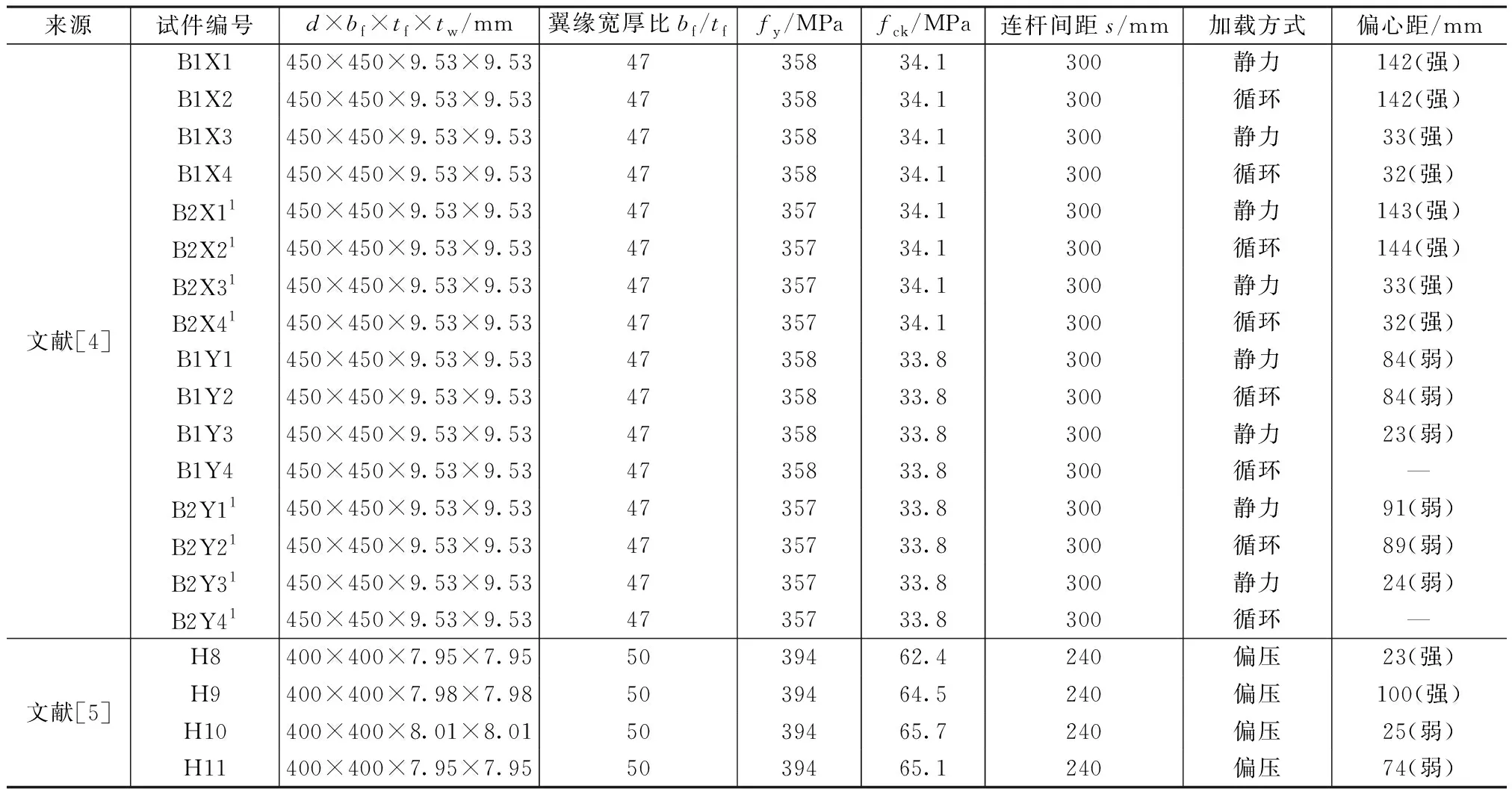
普通强度混凝土和高强混凝土PEC柱参数 表1
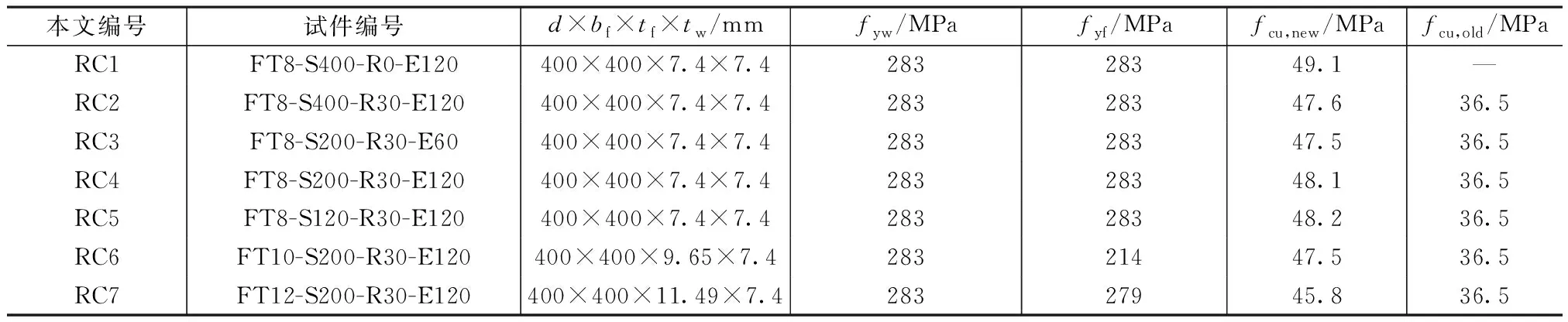
再生混合混凝土PEC柱参数(文献[14]) 表2
图2为普通强度混凝土PEC柱压弯承载力计算值与试验值对比。强轴压弯(图2(a),(b))时:1)五种方法均安全。2)《矩形钢规》曲线与试验点吻合最好。3)在轴力较大区域,曲线由外向内依次为《矩形钢规》、规范EN 1994-1-1、《组规》、《PEC规程》和规范CSA-S16-09;在轴力较小区域,依次为《组规》、《矩形钢规》、规范EN 1994-1-1、《PEC规程》和规范CSA-S16-09;在轴力很小接近纯弯区域,规范EN 1994-1-1曲线最小。4)《PEC规程》曲线与规范CSA-S16-09曲线接近,仅在轴力较大区域,略超出规范CSA-S16-09曲线。弱轴压弯(图2(c),(d))时:1)《组规》和《矩形钢规》计算在某些情况下偏大。2)规范EN 1994-1-1曲线与试验点吻合较好,《PEC规程》和规范CSA-S16-09曲线相互靠近,且偏安全。3)在轴力较大区域,曲线由外向内依次为《矩形钢规》、规范EN 1994-1-1、《组规》、《PEC规程》和规范CSA-S16-09;在轴力较小区域,依次为《矩形钢规》、《组规》、规范EN 1994-1-1、规范CSA-S16-09和《PEC规程》;在轴力很小接近纯弯区域,规范EN 1994-1-1曲线最小。
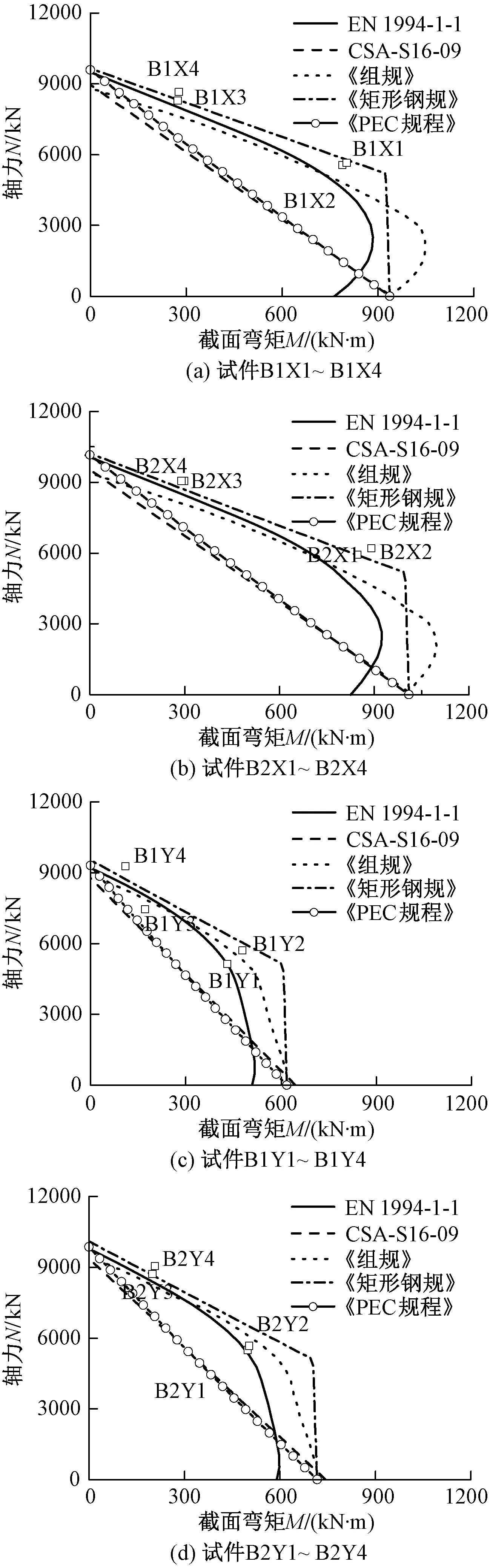
图2 普通强度混凝土PEC柱压弯承载力对比
图3为高强混凝土PEC柱压弯承载力计算值与试验值的对比情况。强轴压弯(图3(a),(b))时:1)五种方法均安全。2)《矩形钢规》与试验点最接近。3)在轴力较大区域,曲线由外向内依次为规范EN 1994-1-1和《矩形钢规》交替包络、《组规》、《PEC规程》和规范CSA-S16-09;在轴力较小区域,依次为《组规》、《矩形钢规》、规范EN 1994-1-1、《PEC规程》和规范CSA-S16-09;在轴力很小接近纯弯区域,规范EN 1994-1-1为最小。4)《PEC规程》曲线与规范CSA-S16-09曲线接近,仅在轴力较大区域,略超出规范CSA-S16-09曲线。弱轴压弯(图3(c),(d))时:1)部分试验点落于《矩形钢规》曲线内。2)在轴力较大区域,五条曲线由外向内的特点与强轴压弯类似;在轴力较小区域,依次为《矩形钢规》、《组规》、规范EN 1994-1-1、规范CSA-S16-09和《PEC规程》;在轴力很小接近纯弯区域,规范EN 1994-1-1为最小,其他四条曲线交替包络。
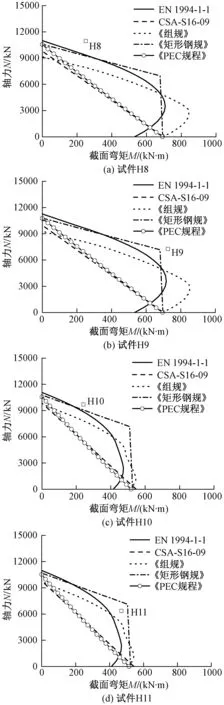
图3 高强混凝土PEC柱压弯承载力对比
图4为再生混合混凝土PEC柱的对比情况,不难看出,对强轴压弯,五种N-M曲线包络关系和高强混凝土类似。
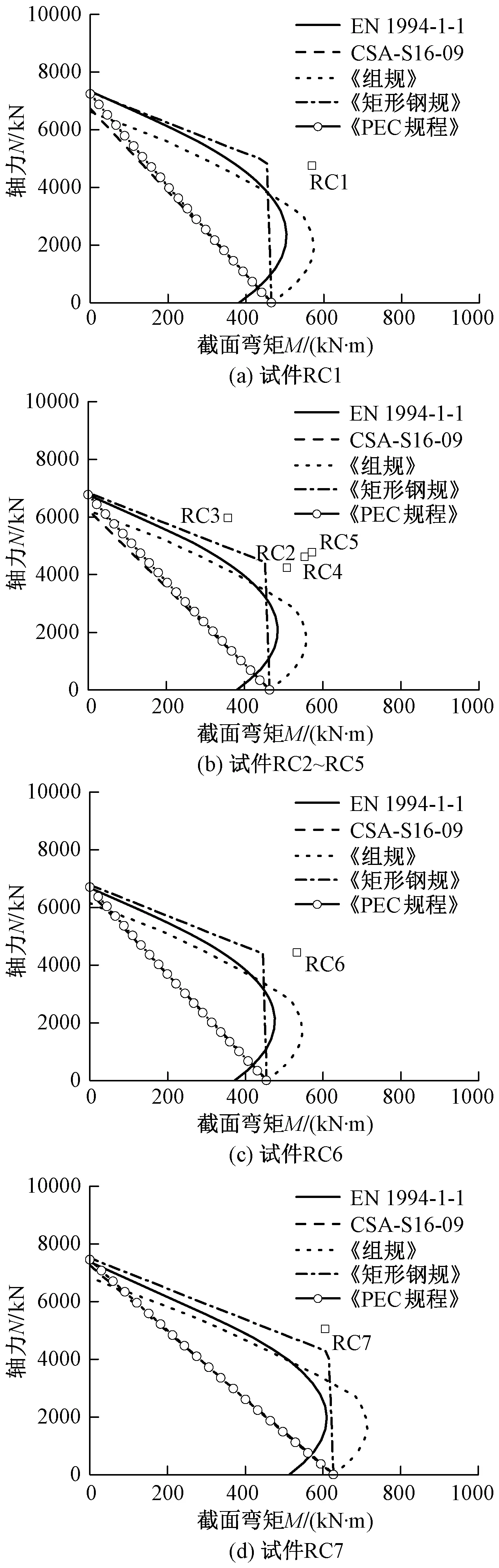
图4 再生混合混凝土PEC柱压弯承载力对比
为比较五种理论曲线与试验点的符合程度,同时综合反映轴力及弯矩两项数据的影响,作试验点和坐标原点之间的连线(该直线表示恒定偏心加载的路径),以该直线与各理论曲线的交点作为相应N-M曲线的理论计算点,规范EN 1994-1-1、规范CSA-S16-09、《PEC规程》、《组规》和《矩形钢规》分别用点p1,p2,p3,p4,p5表示,原点距分别以d1,d2,d3,d4,d5表示,试验点的原点距用dt表示,如图5所示。分别利用理论计算点及试验点的轴力和弯矩计算各自的原点距,求出理论计算点和试验点的原点距的比值,详见表3~5。
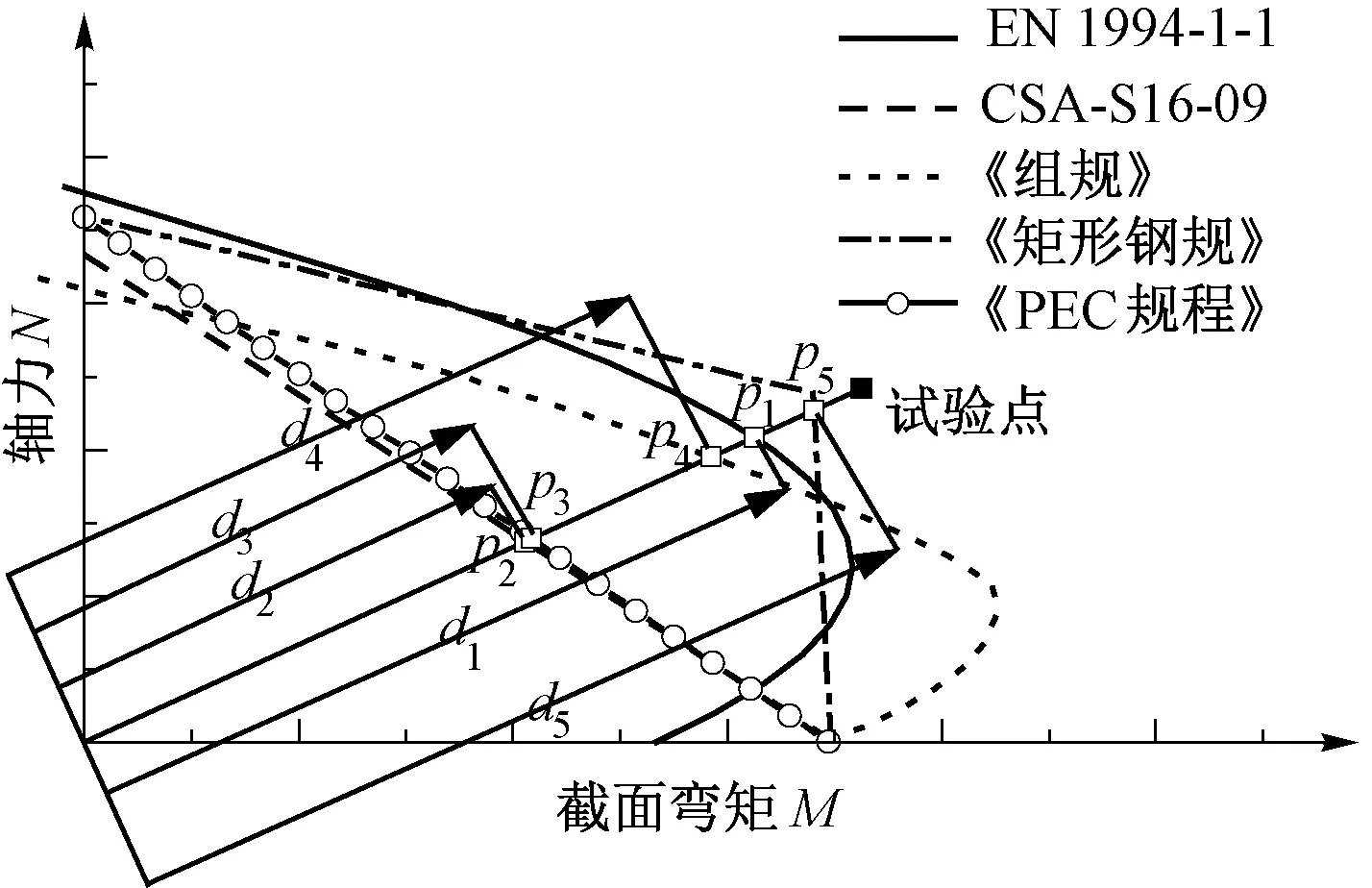
图5 相关曲线理论计算点的确定
表3为普通混凝土PEC柱强轴和弱轴压弯承载力理论值与试验值比较,规范EN 1994-1-1曲线的原点距比值d1/dt对强轴和弱轴的平均值分别为0.926和0.968。规范CSA-S16-09对应的d2/dt的平均值分别为0.742(强轴)和0.805(弱轴)。《PEC规程》对应的d3/dt的平均值为0.764(强轴)和0.812(弱轴),与规范CSA-S16-09接近。《组规》对应的d4/dt的平均值为0.909(强轴)和0.995(弱轴)。《矩形钢规》对应的d5/dt的平均值为0.990(强轴)和1.048(弱轴)。可见,与强轴压弯的试验点相比,规范EN 1994-1-1、规范CSA-S16-09、《PEC规程》和《组规》均偏安全,《矩形钢规》与试验点吻合最好;与弱轴压弯的试验点相比,《组规》计算结果与试验点吻合较好。
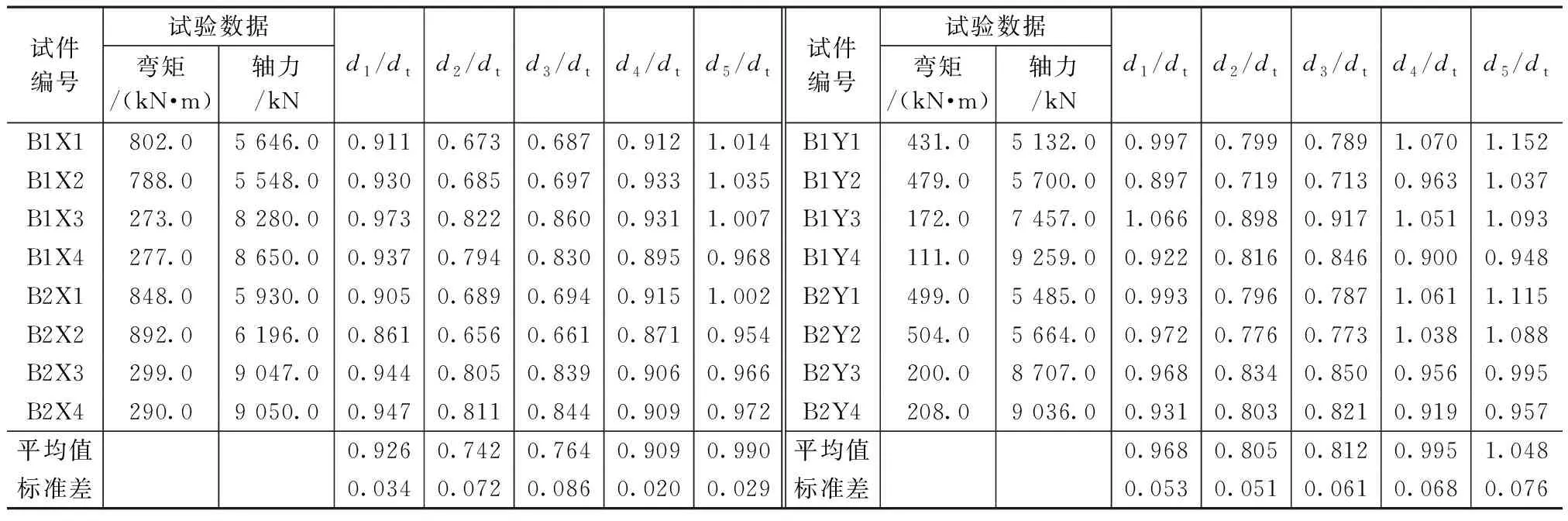
普通混凝土PEC柱理论值与试验值比较 表3
表4为高强混凝土PEC柱强轴和弱轴压弯承载力理论值与试验值比较,规范EN 1994-1-1对应的d1/dt的平均值分别为0.868(强轴)和0.910(弱轴);规范CSA-S16-09对应的d2/dt的平均值分别为0.622(强轴)和0.682(弱轴);《PEC规程》对应的d3/dt的平均值为0.642(强轴)和0.678(弱轴),与规范CSA-S16-09接近;《组规》对应的d4/dt的平均值为0.778(强轴)和0.871(弱轴);《矩形钢规》对应的d5/dt的平均值为0.901(强轴)和1.012(弱轴)。可见,与强轴和弱轴压弯的试验点相比,《矩形钢规》与试验点最接近,其余四类曲线均偏安全。

高强混凝土PEC柱理论值与试验值比较 表4
表5为再生混合混凝土PEC柱强轴压弯承载力理论值与试验值比较,规范EN 1994-1-1中d1/dt、规范CSA-S16-09中d2/dt、《PEC规程》中d3/dt、《组规》中d4/dt和《矩形钢规》中d5/dt的平均值分别为0.801,0.547,0.621,0.798,0.846,五类规范对试验点的预测均偏安全。
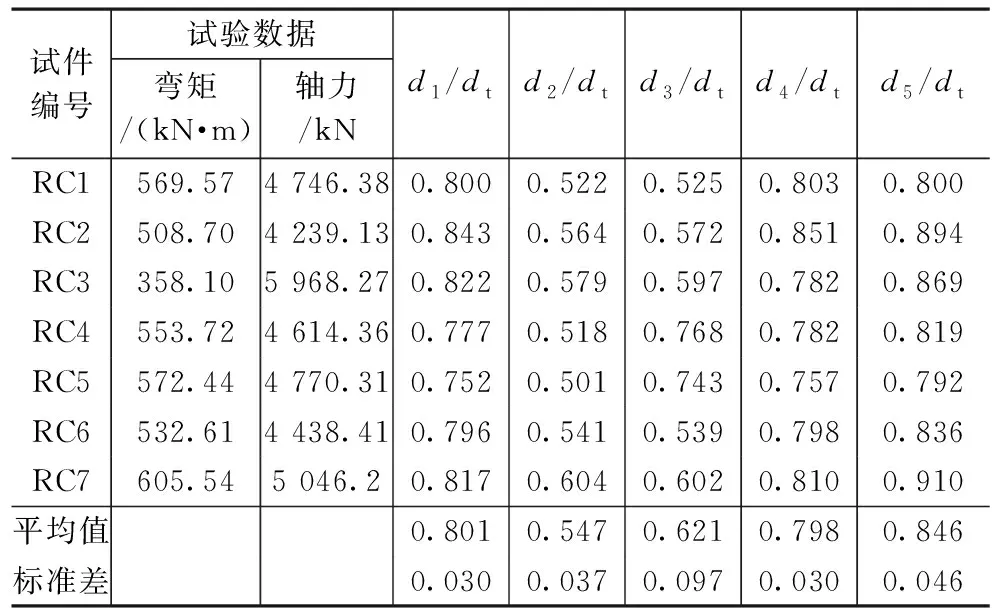
再生混合混凝土PEC柱理论值与试验值比较 表5
3 结论
对比五类规范的N-M相关曲线理论计算点和试验数据,可以发现:规范EN 1994-1-1曲线是各种试验点的下包线,规范EN 1994-1-1和《组规》曲线均具有外凸特性;《PEC规程》曲线与规范CSA-S16-09曲线较为接近,且均偏保守;《矩形钢规》曲线为外凸折线,与试验值吻合较好。
