基于三维随机场的地下洞室围岩变形分析
2021-05-13康玉梅于佳月
康玉梅,于佳月
(东北大学 资源与土木工程学院, 辽宁 沈阳 110819)
地下洞室开挖过程中,会造成原岩应力的变化,引起区域变形,若变形超过一定范围,就会对周围环境造成不利的影响,因此,合理分析地下洞室的变形是非常重要的。地下洞室围岩变形问题的复杂性不仅仅在于结构形式多样,更主要是岩土参数的不确定性。大部分学者在研究地下结构问题时,常采用确定性的分析方法,忽略了材料的非均匀性以及各向异性,使得结果存在一定偏差。为了真实地表征岩土参数,Vanmarcke[1]引入了自相关函数和波动范围的概念,构建了考虑参数空间变异性的随机场模型。
目前,国内外学者在随机场的生成[2-3]、应用[4-5]以及基于随机机场理论的可靠度分析方面[6-8]等都进行了深入的研究。其中,李静萍等[9]在K-L级数展开法的基础上,构造了响应面函数并进行可靠度分析;李健斌等[10]分析了土体弹性模量的竖向、横向波动距离及变异系数对隧道施工地层变形的影响;王长虹等[11]研究了内聚力、内摩擦角和压缩模量的空间变异性,将随机场理论中横向相关距离和纵向相关距离取为相同值,对地表沉降进行可靠度分析。刘学军等[12]建立了二维各向同性随机场,研究了岩体抗剪强度的空间变异性对隧道变形的影响。胡长明等[13]提出了边坡二维随机场的一维局部平均过程,得到了局部均值与局部方差的计算公式。可见,在以往对参数空间变异性的研究中大多考虑竖向及横向变异性对结构的影响,即采用二维随机场模拟岩土体的变形,但在实际工程中,由于结构以及赋存环境的复杂性,采用二维随机场模拟具有一定局限性。
鉴于此,本文建立三维有限差分模型,采用K-L级数展开法生成三维随机场,研究弹性模量E在三个方向的波动范围(即横向、纵向、竖向波动范围)对地下洞室围岩变形的影响规律。
1 计算模型
1.1 有限差分模型
参考乌东德水电站右岸4#导流洞的Ⅰ层开挖实例[14],其开挖尺寸:横断面宽度为19.9 m,高度为9 m,取随机场的模型尺寸为60 m×40 m×60 m,外围区域为100 m×40 m×60 m,地下洞室有限差分网格模型见图1。由于弹性模量的变异系数较大[14],因此,选取弹性模量E的空间变异性作为研究重点,其它具体的岩体力学参数见表1。
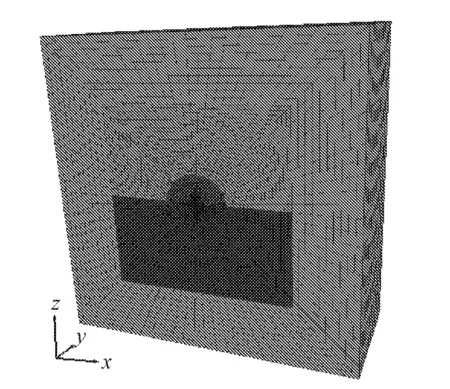
图1 地下洞室有限差分网格模型

表1 岩体力学参数
1.2 随机场模拟
为研究弹性模量E的空间变异性,将岩体弹性模量在计算区域模拟为三维随机场,弹性模量服从对数正态分布,其均值为2.55 GPa,变异系数为0.22,三维各向异性高斯自相关函数类型可表示为[15]:
(1)
式中:δx,δy,δz分别为横向波动范围、纵向波动范围和竖向波动范围;τx,τy,τz分别为横向、纵向和竖向距离。
利用K-L级数展开法生成随机场,以自相关函数ρ(x1,x2)为基础,将参数随机场离散为:
(2)
式中:μ和σ为高斯随机场的均值和标准差;λi和fi(x1,x2)为自相关函数ρ(x1,x2)的特征值和特征函数;ξi(θ)为独立标准正态随机向量;x1、x2为随机场区域中的任意坐标点;θ为外部空间坐标。
由式(2)可知,随机场不仅取决于位置,还取决于标准随机变量、特征值和特征函数。特征值、特征函数与自相关函数的类型、波动范围有关,本文仅考虑波动范围的不同引起随机场的变动,进而分析上覆岩层的变形规律。因此,将式(2)中的ξi(θ)取为定值,不随每次模拟的变化而变化。
一般岩土体的横向波动范围δx在10 m~80 m之间,竖向波动范围δz在1 m~5 m之间[16]。为模拟不同波动范围情况下开挖岩层的变形特性,设置工况如表2所示,并将计算结果与弹性模量均值为2.55 GPa时(工况D)的确定性分析结果进行比较。
采用K-L级数展开法生成弹性模量随机场,得到分布情况如图2、图3所示。图2表示弹性模量E的一维随机场分布情况,由图2可知,在一维情况下随机场的分布变化幅度较小,但具有一定的连续性;图3表示弹性模量E的二维随机场分布情况,其中,1表示弹性模量E的数值大,2表示弹性模量E的数值小,由图3可知,弹性模量E的二维随机场变化幅度较大,且其分布具有平稳性、连续性、光滑性等特征。值得注意的是,三维随机场需要采用四维空间才可以表达,而四维空间无法用图形简单表示,因此,并不展示弹性模量的三维随机场分布情况。
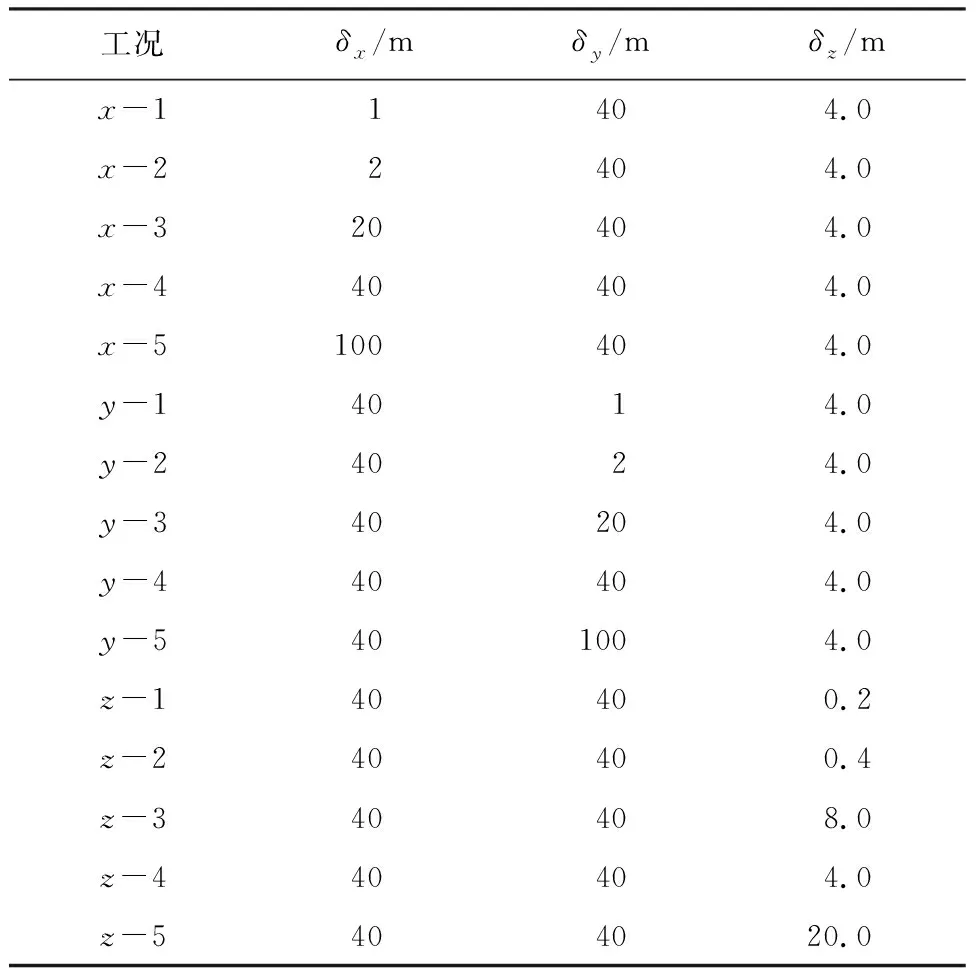
表2 随机分析计算工况
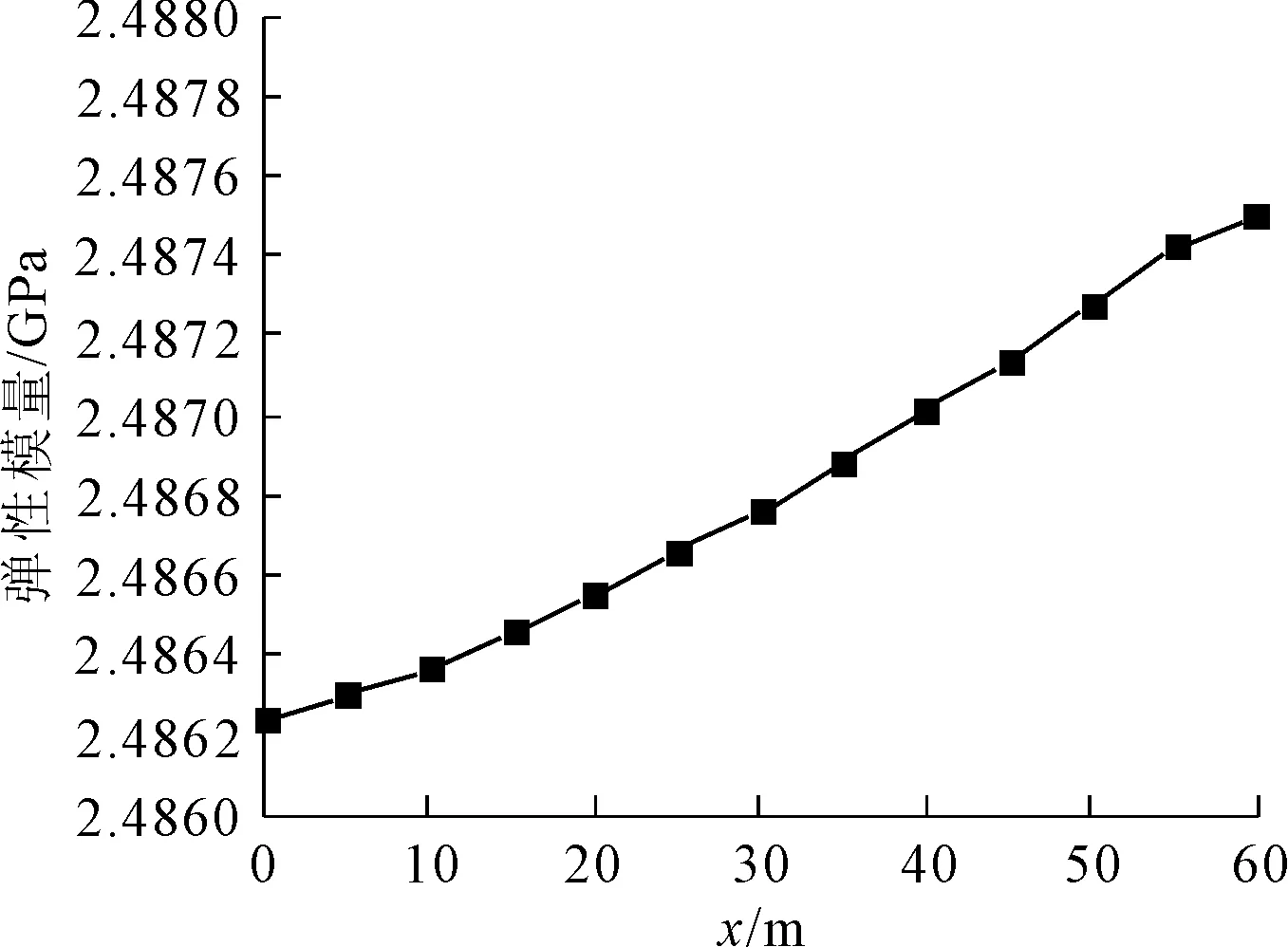
图2 弹性模量一维随机场分布
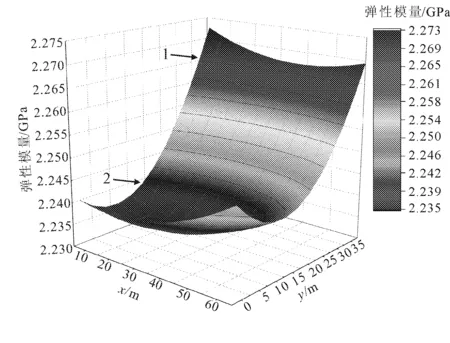
图3 弹性模量二维随机场分布
2 基于随机场的围岩变形分析
施工过程中合理控制围岩变形至关重要,为研究地下洞室上覆岩层的变形情况,在地下洞室上方布置测线,其位置如图4所示。
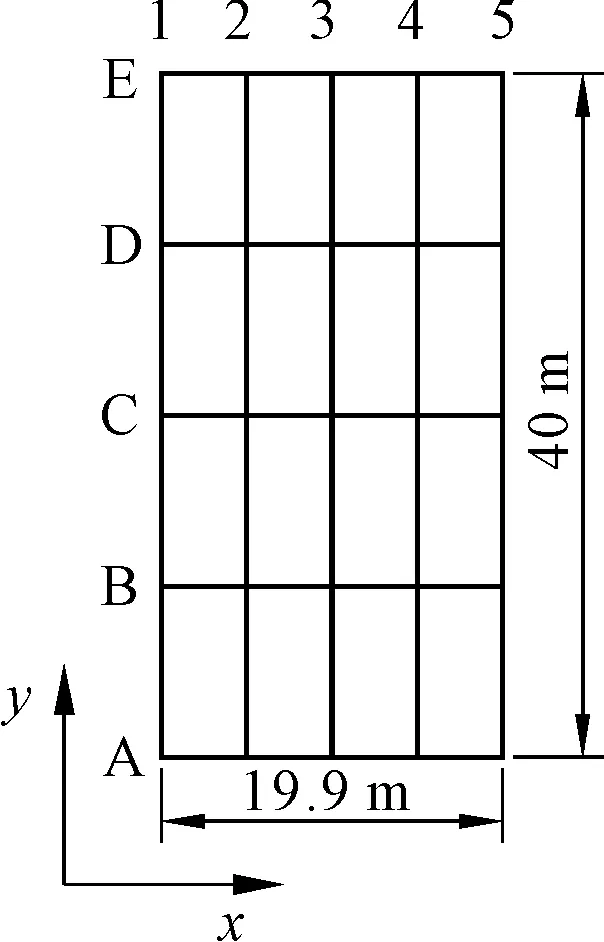
图4 开挖区域上覆岩层测线位置
2.1 不同横向波动范围
图5给出了弹性模量E在横向波动范围变化情况下测线3处围岩的竖向位移变化曲线。由图5可知:在横向波动范围不断变化的情况下,位移值在确定性分析结果上下浮动,且横向变异性越大,位移值相对于确定性分析结果的变化越明显;此外,沿纵向深度的增加,竖向位移也有减小的趋势,但变化幅度不大。图6给出了在横向波动范围变化的情况下,测线C处围岩的竖向位移,可以更清楚的看到,洞室轴线位置处的竖向位移最大,其受空间变异性的影响更大。其它测线结果与测线3、测线C结果相似,篇幅所限,不再赘述。
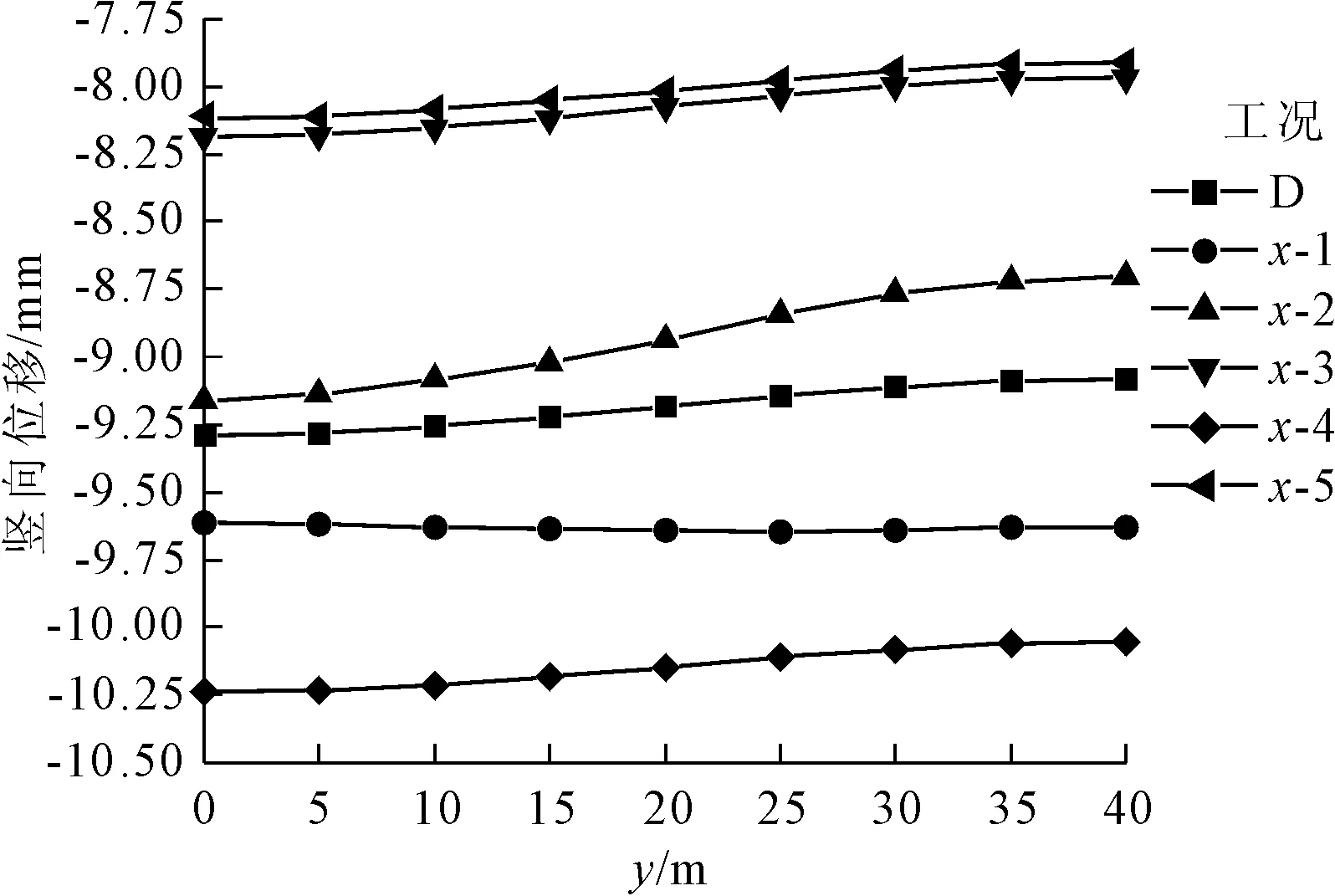
图5 不同横向波动范围下围岩竖向位移(测线3)
2.2 不同纵向波动范围
同样,我们可以得到弹性模量E在不同纵向波动范围情况下测线3处围岩竖向位移变化规律,如图7所示。由图7可知:随着纵向波动范围的不断变化,位移值在确定性分析结果的上下浮动,且纵向变异性越大,位移值相对于确定性分析结果的变化越明显;随着纵向深度的增加,竖向位移也有减小的趋势,但变化幅度不大。不同纵向波动范围情况下测线C处围岩竖向位移变化如图8所示,从图8可以看出,洞室轴线位置处的竖向位移最大,且其受空间变异性的影响更大。
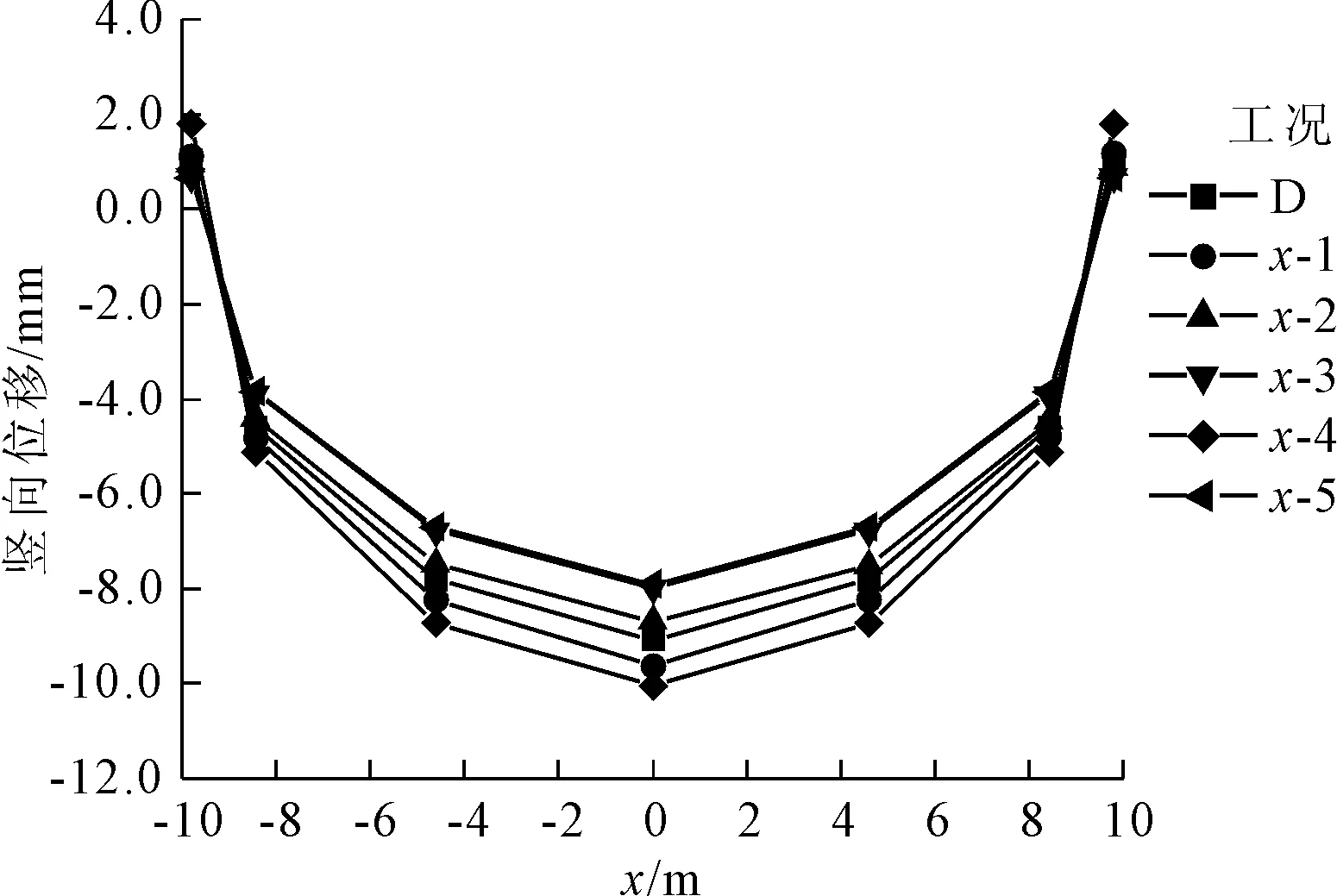
图6 不同横向波动范围下围岩竖向位移(测线C)
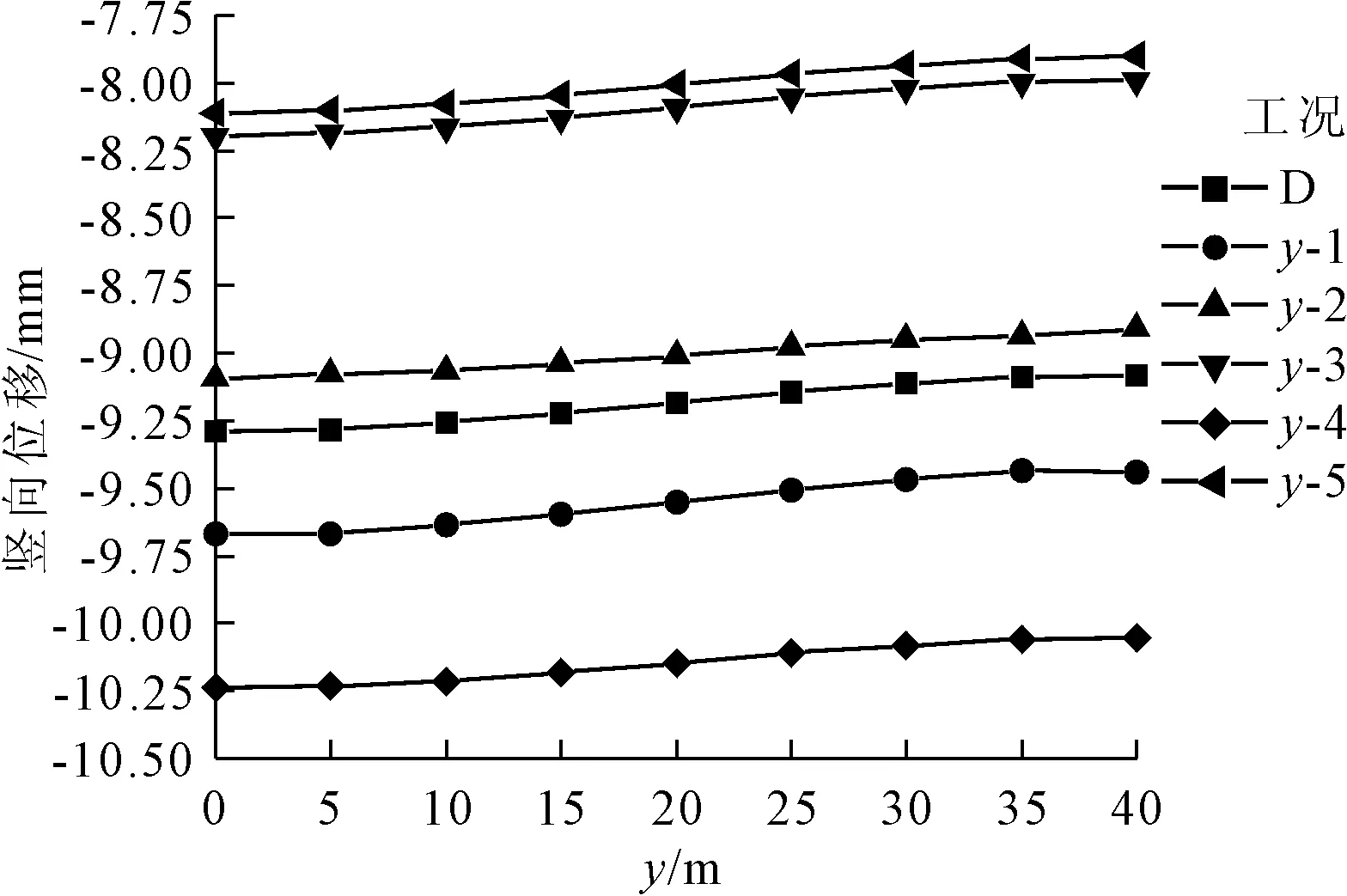
图7 不同纵向波动范围下围岩竖向位移(测线3)
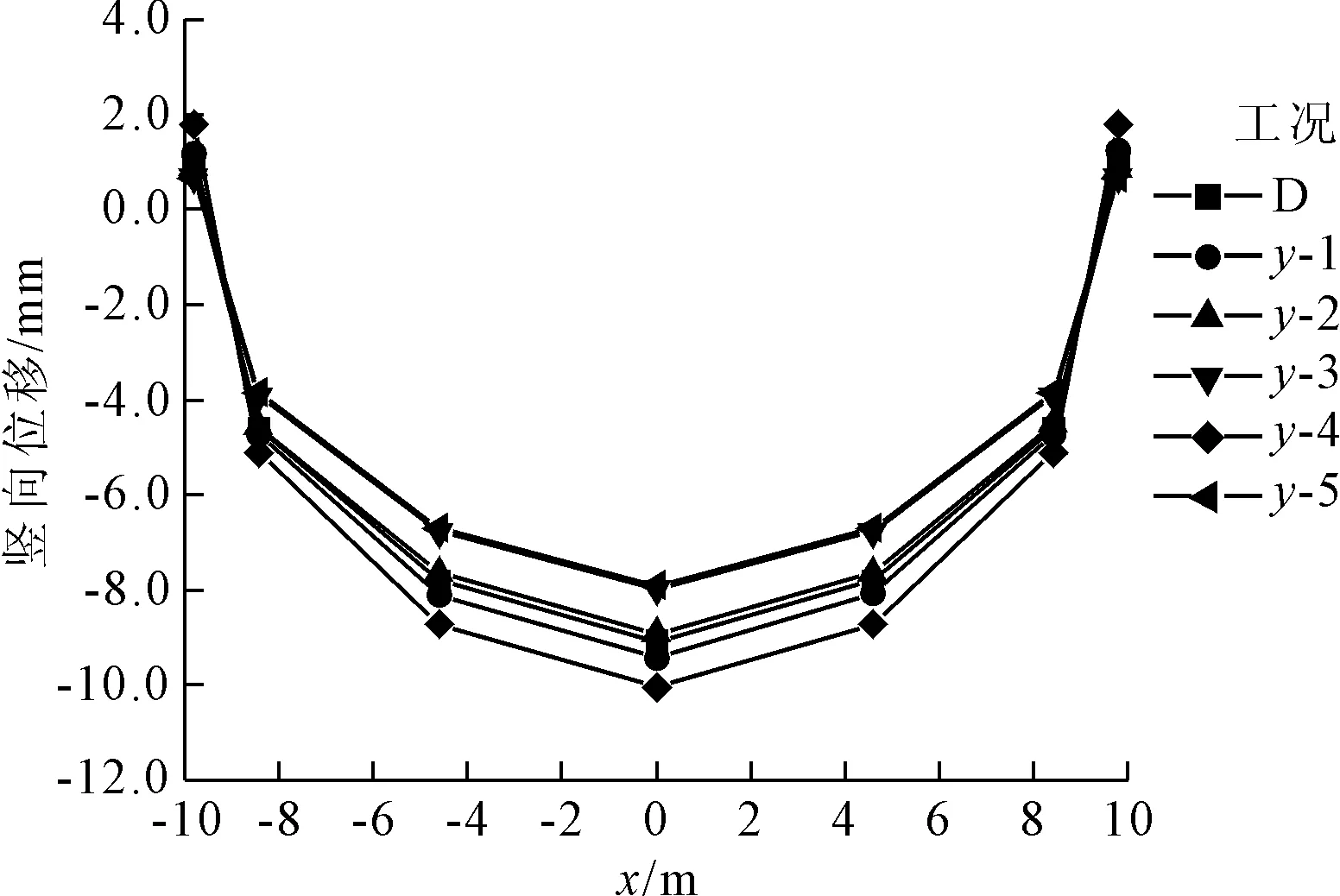
图8 不同纵向波动范围下围岩竖向位移(测线C)
图9表示不同横向波动范围以及不同纵向波动范围在测线3处位移变化的对比曲线,从图9可以清晰地看出:随着波动范围的不断增加,横向以及纵向波动范围对于位移的影响逐渐趋于一致,当波动范围为40 m和100 m时,二者的曲线几乎重合。
2.3 不同竖向波动范围
类似地,图10给出了弹性模量E在不同的竖向波动范围下测线3处围岩的竖向位移变化曲线。
由图10可知:随竖向波动范围的增加,围岩的位移值在确定性分析结果的上下浮动,且随着波动范围的增加,位移值相对于确定性分析结果的变化越明显;竖向位移沿y方向也有减小的趋势,但变化幅度不大。测线C处围岩的竖向位移如图11所示,由图11可以看出:竖向位移最大值在洞室轴线位置处,且其受空间变异性的影响更大;相对于横向以及纵向波动范围,竖向波动范围对于位移的敏感性更大。
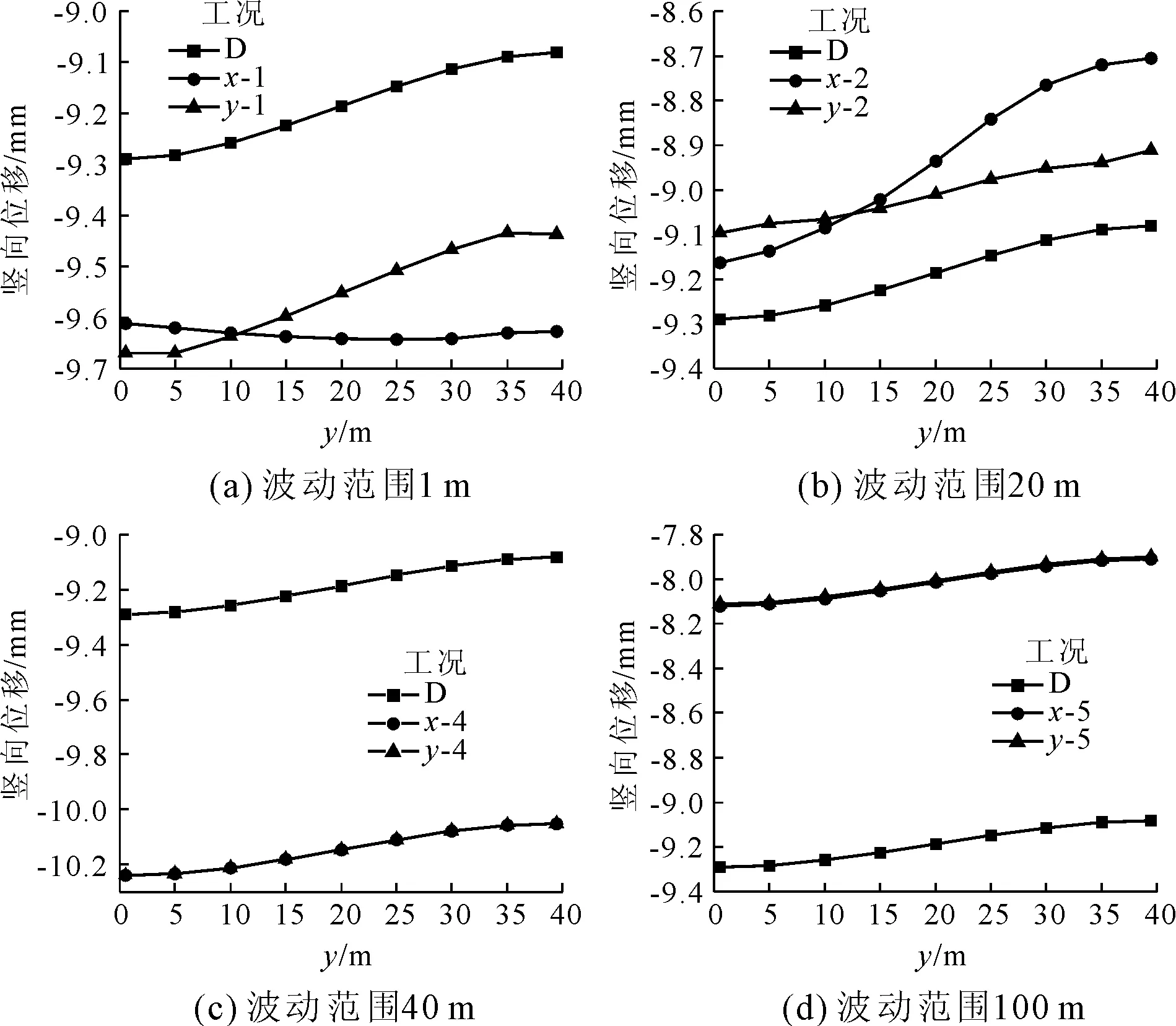
图9 不同横向、纵向波动范围下位移对比
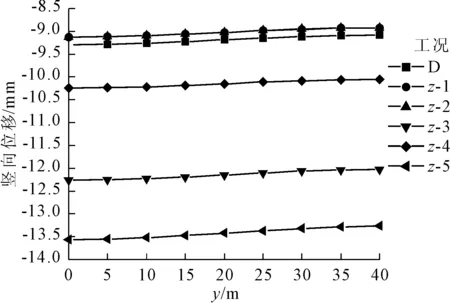
图10 不同竖向波动范围下围岩竖向位移(测线3)
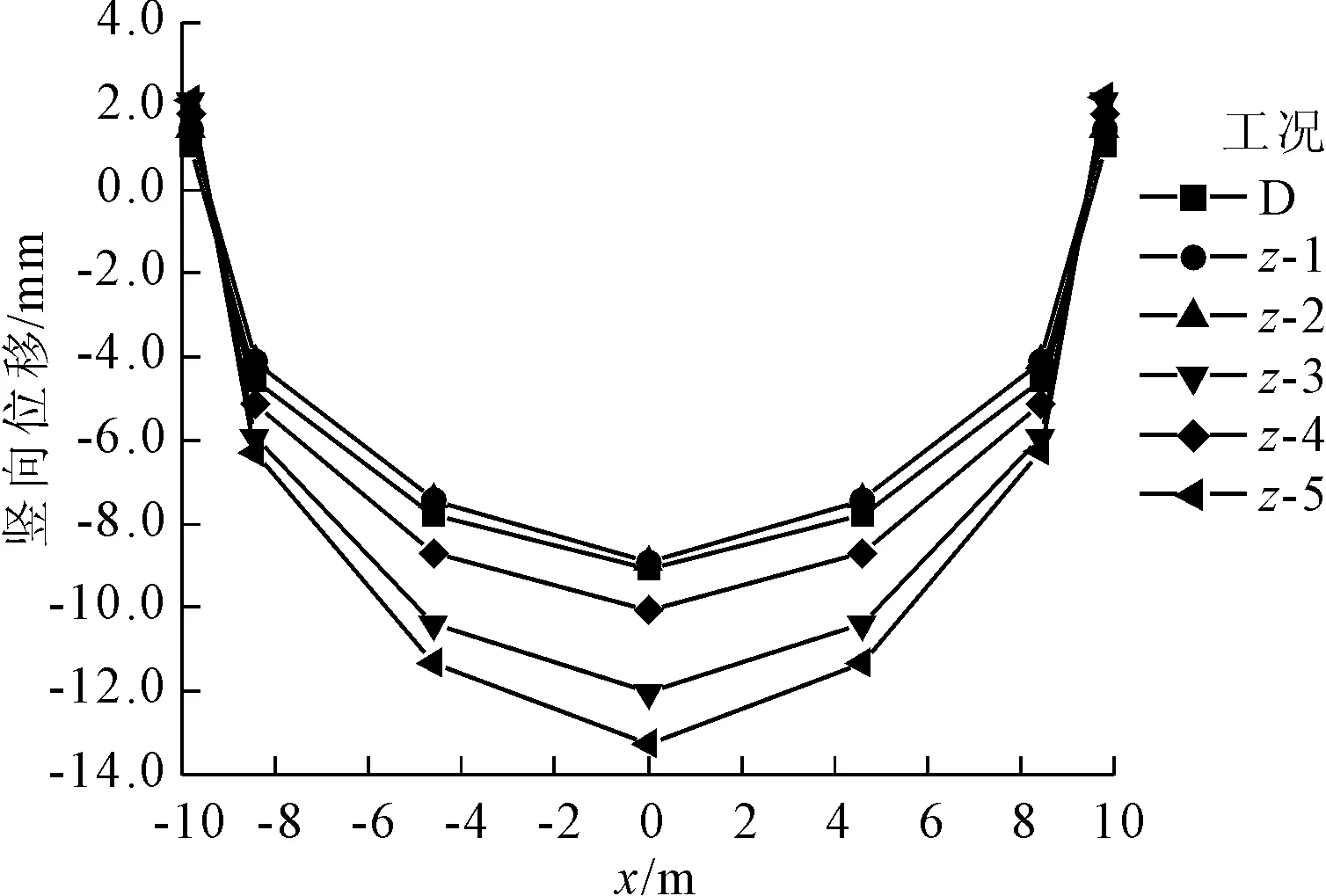
图11 不同竖向波动范围下围岩竖向位移(测线C)
3 结 论
全面分析地下洞室开挖引起的围岩变形是工程中的关键问题。本文采用K-L级数展开方法生成弹性模量E的随机场,并利用有限差分软件FLAC3D模拟围岩变形,研究了弹性模量E三个方向的波动范围对地下洞室变形的影响规律。
(1) 随着波动范围的不断增加,横向和竖向波动范围对位移的影响逐渐趋于一致,当波动范围大于40 m时,二者的曲线几乎重合,说明在考虑参数空间变异性时,纵向波动范围与横向波动范围对围岩变形都有着重要影响,不可忽略。
(2) 当竖向波动范围小于0.4 m时,地下洞室围岩的变形值不会发生较大的改变;相对于横向和纵向波动范围,竖向波动范围对于位移的敏感性更大,表明在实际工程中更应该着重考虑弹性模量的竖向波动范围。
(3) 随着波动范围的增加,位移值相对于确定性分析结果的变化越明显,且洞室轴线位置受空间变异性的影响更大。由此可见,岩土参数弹性模量的空间变异性对地下洞室上覆岩层变形有着重要的影响。
