重庆市典型下垫面SCS-CN模型基于坡度修正的径流曲线数优化

雷晓玲，卫 娇，魏泽军，刘 宁

(1.重庆交通大学， 重庆 400074； 2.重庆市科学技术研究院， 重庆 401123；3.重庆市设计院， 重庆 400015)

“海绵城市”的提出为解决水资源短缺和城市内涝问题提供了新思路[1-2]，地表径流量是海绵城市建设中最重要的控制指标。美国土壤保持局(Soil Conservation Service，SCS)[3-5]研发的的径流曲线数模型(Soil Conservation Service Curve Number Method，SCS-CN)因其结构简单、模拟精度较高，被广泛用于径流预测。王冬等[6]将SCS-CN模型应用于湖北省松柏站流域的洪水预测。徐田婧等[7]采用SCS-CN模型估算了南京市尺度大面积屋顶绿化的暴雨径流削减效果。吴安坤等[8]利用SCS-CN模型估算出贵阳市区不同重现期降雨产流量，从而评价了城市内涝灾害风险。

径流曲线数(CN)是SCS-CN模型中用于反映某流域特征的综合参数，主要与土壤类型、植被覆盖、土地利用方式、前期土壤湿润程度(Antecedent Moisture Condition，AMC)、地形坡度等因素有关[9]。由于存在广泛的地域差异，美国土壤保持局提供的CN值在我国不适用。在研究区域有一定长度年限的降雨径流资料时，则可利用已有数据来反推CN值。现有研究已经提出直接计算法[10]、平均值法[11]、算术平均值法[11]、中值法[11]、渐近线法[12]、S对数频率分布法[13]等方法来反推CN值。符华素等[14]根据北京密云3个小区实测降雨径流资料，对比了用不同方法反推CN值计算径流深的优劣，结果表明由算术平均值法得到的CN 值更符合该研究区域实际情况。胡晓静等[15]基于北京山区坡地径流场 2007—2013年的降雨径流观测数据，利用算术平均值法计算了山区不同土地利用、土壤水文组的 CN值，得到了较为可靠的径流估算结果。重庆市地形高差较大，而坡度是影响地表径流的重要因子[16]，但SCS-CN模型未将坡度因子考虑在内。本文通过开展人工模拟降雨实验，对重庆市典型区域的CN值进行坡度修正，以期为山地城市的水文预测、防洪排涝设计、雨水的收集利用等提供借鉴。

1 研究区域及方法

1.1 研究区域概况

重庆市位于我国西南部，属于我国第一、二阶梯的交叉地段，地形高差较大，其中山地面积约占76%，是三峡库区面积最大的山地城市。该地区气候主要为亚热带季风气候，多年平均降雨量为1 125 mm。重庆市土地开阔，紫色土和黄壤分布较广，分别约占全市土地总面积的33.22% 和28.78%，见图1[17]。全市土地坡度分布情况：<5°所占比例为44.78%；5°～15°占14.48%；15°～25°占20.99%，见图2[17]。渝北区和巴南区两大区域面积占据重庆主城区的一半以上，区域内广泛分布着紫色土和黄壤。

图1 重庆市土壤分布图

图2 重庆市坡度分布图

1.2 实验装置

为了在较短时间内获取较为可靠的降雨径流数据，采用室内人工降雨的方式于2018年3月至2018 年10 月进行实验研究。实验装置由降雨装置及下垫面装置两部分组成，见图3。人工降雨装置主要由供水系统、控制系统、智能终端和采集系统四部分构成，采用喷头型便携式人工模拟降雨器。下垫面模拟装置采用MSS-M型手摇式变坡实验钢槽，在槽体底部和侧端开孔分别收集降雨过程产生的土壤下渗量和土体表面的径流量，可通过手摇柄变换坡度(可调节范围为0°～ 45°)。为保证数据的准确性，采用两套移动式钢槽系统同时进行实验。

1.3 实验方法

(1) 降雨参数设置。通过查阅相关文献并结合重庆市的实际情况确定各降雨事件的降雨强度和降雨历时。根据重庆市雨量充沛、雨型急促、降雨历时短、短时形成暴雨或强降雨的特点[18]，设置实验降雨参数参考值如表1所示，实际值以降雨设备智能终端导出的最终降雨量为准。

图3 人工降雨装置喷头(右上)及下垫面装置图

表1 人工降雨参数设计值

(2) 下垫面布置和坡度设置。下垫面模拟装置布置情况见表2。水文土壤类型主要反映土壤本底条件下的水文类型，根据土壤特性将其划分成A、B、C、D四类。本实验所用紫色土属于B类土壤，黄壤属于C类土壤。

表2 下垫面参数表

根据重庆市地形坡度资料设置本次实验下垫面坡度为微坡1组、缓坡2组和较陡坡1组，坡度参数见表3。

(3) 实验监测指标。实验监测指标分别为由人工模拟降雨设备智能终端系统导出的降雨量(mm)、由移动钢槽系统侧端出水口收集的地表径流量(mm)和钢槽槽体底部开孔收集的土壤下渗量(mm)。

表3 下垫面坡度参数表

2 模型概述

2.1 模型原理

SCS-CN径流模型是20世纪50年代美国农业部的水土保持局(USDA，SCS)[3-5]开发的用来估算地表径流的小流域水文模型[19]。该模型基于水量平衡方程和以下两个基本假定[3]：实际入渗量(F)与实际径流量(Q)的比值等于流域潜在入渗量(S)与潜在径流量(P-Ia)之比；初损值(Ia)是潜在入渗量(S)的一部分。最终推导得出以下公式：

(1)

(2)

式中：P为降雨量，mm。

将人工降雨实验获取的场次降雨径流数据带入式(1)，式(2)计算出对应降雨事件下的CN值，然后取算术平均值得到最终CN值。

考虑前期土壤湿润程度(AMC)对径流的影响，美国土壤保持局在SCS-CN模型中引入了前期降水指数API(Antecedent Precipitation Index,API)，即土壤前5 d降雨总量。根据前5 d降雨总量将前期土壤湿润程度划分为三个等级，其对应的划分标准见表4[20-21]。本研究人工降雨实验通过合理安排场次降雨量及雨前间隔期，控制前期土壤湿润程度(AMC)均处于正常状态下。

表4 前期土壤湿润程度分类

三种土壤湿润状态下的CN值的关系式如下：

CNⅠ=CNⅡ-

(3)

CNⅢ=CNⅡexp[0.00673(100-CNⅡ)]

(4)

式中：CNⅠ，CNⅡ和CNⅢ分别表示前期土壤湿润程度为干旱、正常和湿润状态下的CN值。

2.2 坡度修正公式

(1) Williams坡度修正公式。为减少坡度变化对径流预测结果的影响，Williams等[3]在SCS-CN模型中引入坡度因子，提出了前期土壤湿润程度为正常条件下修正CN值的可行公式：

(5)

式中：CNⅡ(W)表示经Williams坡度修正公式修正后的CN值；slp表示下垫面平均坡度。

(2) Huang坡度修正公式。我国学者Huang等[22]根据黄土高原地区牧草和苜蓿两种植物覆盖下的9个坡度条件下的下垫面降雨径流数据，对Williams坡度修正公式进行改进，提出了适用于大坡度区域的CN值修正公式，得到了较好的径流预测效果。Huang等得出的坡度修正公式如下：

(6)

式中：CNⅡ(H)表示经过Huang坡度修正公式修正后的CN值；其余符号含义同式(5)。

2.3 模型评价参数

为了比较坡度修正前后的CN值对SCS-CN模型径流计算精度的影响，选用模型效率系数(E)和相对误差(RE)两个参数作为评价指标。

(1) 模型效率系数。模型效率系数(E)用以评价计算值和实测值的接近程度，取值范围为-∞～1。其计算公式如下：

(7)

(2) 相对误差。相对误差(RE)主要反映计算值和实测值的偏差程度。其计算公式如下：

(8)

各符号含义同式(7)。

一般而言，将实测径流深(Robsi)的20%作为单次降雨事件的允许误差[23]。

3 结果与分析

3.1 坡度对径流深的影响

为研究坡度变化对地表径流深的影响，对每个下垫面分别选取4 场典型降雨场次的径流数据进行分析。各下垫面不同坡度条件下的降雨径流特征变化见图4。

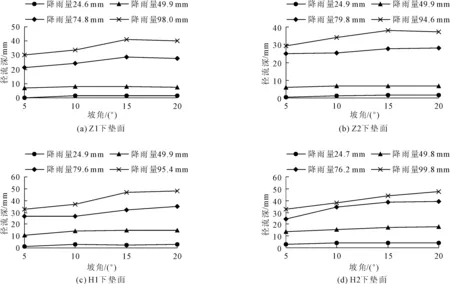
图4 坡度对径流深的影响

由图4可以看出，同一坡度下，某一下垫面的地表径流深随降雨量的增大而增大。同时，下垫面的径流系数也随着降雨量的增大而增大，即有更多的降水转化为地表径流。如Z1下垫面在5°坡度条件下，降雨量从24.6 mm增大到98.0 mm时，该下垫面的径流深由0.21 mm增加到30.31 mm，对应的径流系数由0.01增加到0.31。这种现象的产生与下垫面的潜在蓄水能力S有关，降雨初始阶段，部分雨水被植物截留，降落在地面上的雨水则渗入土壤以及填补坑洼，此时雨水下渗速度较快，地表径流难以产生或产生速度较慢。随着降雨时长的增加，当土壤的蓄水量达到饱和或降雨强度大于入渗强度后，雨水难以下渗，此时多余的雨水开始沿着地表流动并汇集形成坡面径流。因此，在降雨量较小的条件下，土壤蓄水能力S未达到饱和，降雨大部分被植被及土壤吸收，产生的径流量较小，径流系数也较小。而当强降雨事件发生时，土壤蓄水能力S很快达到饱和，此时过多的雨水将全部转化为地表径流，径流系数较大。

单次降雨事件发生时，随着坡度的增大，同一下垫面的地表径流深总体上呈现出增大的趋势。该现象表明，坡度变化对径流深产生了显著影响。这可能与坡向势能随坡度增大而增加有关[24]。坡向势能增加使得坡面水流速率增大，从而使径流入渗时间缩短，入渗量减小，最终导致地表径流量增大[25]。然而在坡度15°～20°之间，部分场次降雨的径流深几乎没有增加甚至出现减小的趋势。如Z1下垫面在降雨量为74.8 mm 的情况下，坡度由15°增加到20°时，其径流深由28.53 mm 减少到27.65 mm。有学者[26]在坡度对坡面物质迁移特性的试验中发现，降雨量一定时，径流量在坡度15°左右达到最大值，此时可能存在临界坡度现象[27]。

3.2 基于坡度修正的CN值

根据水文土壤类型和土地利用方式查阅美国水土保持局提供的CN值表可以得到各下垫面CN值，即CNⅡ。此外，根据获取的四种坡度下的人工降雨径流数据，利用算术平均值法反推CN值得到CNⅡ(算)，在此基础上分别利用Williams坡度修正公式和Huang坡度修正公式计算得到各下垫面的CNⅡ(W)及CNⅡ(H)，结果见表5。

表5 坡度修正前后CN值

由表5可知，查CN值表所得的CN值最大且明显高于其他方法计算所得CN值；由算术平均值法反推得到的CNⅡ(算)与Huang坡度修正公式修正后的CNⅡ(H)较为接近；Williams坡度修正公式得到的CNⅡ(W)较CNⅡ(算)和CNⅡ(H)略大；同一类型下垫面的CN值随坡度的增大出现一定程度的增大。

同一坡度条件下，不同下垫面的CN值存在H2>H1>Z2>Z1，即黄壤>紫色土，自然草地(稀疏)>自然草地(浓稠)。其原因一方面是紫色土中含有部分黏土，土质较为松软，土壤本身能保持大量的水分，因而产生的径流量较少；而黄壤中所含风化岩石较多，不能很好地吸收水分，土壤保水性较差，降水较多地转化为地表径流。另一方面，植被茂密的根系对降落到地表的雨水有较好的保持和吸收作用，降落到地面的雨水被植被的叶片和根系截留、吸收了较大部分，少部分汇集产生地表径流。

3.3 模型评价参数分析

坡度修正前后计算径流深与实测径流深的对比如图5所示，查表法和Williams坡度修正公式的计算值较离散地分布在实测值1∶1线的上方，而算术平均值法和Williams坡度修正公式的计算值则较集中地分布于实测值1∶1线的两侧。

图5 坡度修正前后计算径流深与实测径流深比较

从模型效率系数E来看(见图6)，整体而言，查表法的模型效率系数最低。使用Williams坡度修正公式引入坡度因子的影响后，模型效率系数较算术平均值法有所减少。而经Huang坡度修正公式优化后得到了较好的径流估算结果，各下垫面的模型效率系数较修正前进一步提高。

图6 坡度修正前后模型效率系数比较

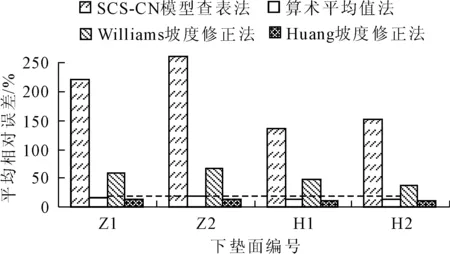
图7 坡度修正前后平均相对误差比较

4 结 论

(1) 坡度变化对径流深具有显著影响，总体而言，地表径流深随坡度的增加而增大。

(2) 基于Williams坡度修正公式和Huang坡度修正公式，优化得到不同植被覆盖程度的紫色土和黄壤下垫面在不同坡度下的CN值。同一类型下垫面的CN值随坡度的增大出现一定程度的增大；同一坡度下的CN值存在黄壤>紫色土，自然草地(稀疏)>自然草地(浓稠)。

(3) 经对比，由Huang坡度修正公式修正后的模型效率系数最高且平均相对误差最小，得到的计算径流深满足模型精度要求。而Williams坡度修正公式得到的径流预测结果超过了允许误差，对研究区域的径流预测效果不佳。因此，在计算山地城市CN值时，建议使用Huang坡度修正公式进行优化，以便获取更加精确的径流估算结果。