输电线脱冰过程中耐张串金具的受力仿真分析
2021-05-13刘小会叶中飞
李 春,刘小会,2,黄 睿,叶中飞,伍 川,张 博
输电线脱冰过程中耐张串金具的受力仿真分析
李 春1,刘小会1,2,黄 睿1,叶中飞3,伍 川3,张 博3
(1. 重庆交通大学土木工程学院,重庆 400074; 2. 重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074; 3. 国网河南省电力公司电力科学研究院输电线路舞动防治技术重点实验室,河南 郑州 450052)
针对脱冰过程中导线张力对输电线连接金具的破坏作用,运用ABAQUS软件分别建立特高压输电线路的导线模型和耐张串连接金具的整体模型。然后基于改变密度法模拟均匀覆冰的六分裂导线和覆冰脱落过程,研究不同步脱冰时各子导线的动态张力和导线束扭转角的变化规律,结果表明未脱冰子导线的动态最大张力大于导线覆冰静态张力,导线动张力与导线束的转角大体呈负相关关系。最后选取导线覆冰静态张力和脱冰引起的导线最大动张力、最小动张力、稳态张力分别施加到耐张串金具模型上进行有限元分析,发现耐张串各连接金具的应力与导线张力的相关关系不一致;对应力较大和存在形状突变的金具进行单独分析,判断其相应的破坏模式,为线路金具设计及优化提供了参考。
ABAQUS;六分裂导线;不同步脱冰;耐张串金具;应力
近年来,我国输电线路冰害事故时有发生,使得人们极其关注输电线路的安全性能[1-3]。导线覆冰及覆冰脱落会引起导线张力的急剧变化,严重时会损坏输电线连接金具。目前部分国内外学者采用静荷载模拟试验[4-7],研究覆冰脱落后导线的跳跃高度及张力变化;也有学者利用ADINA,ANSYS和ABAQUS等有限元软件对导线覆冰脱落进行数值模拟[8-12],详细研究档距、高差等线路参数及覆冰厚度、脱冰位置、不同步脱冰模式对脱冰导线跳跃幅度和张力的影响。目前对脱冰载荷作用下连接金具的应力研究较少,仅有部分学者对连接金具进行了局部分析。PRENLELOUP等[13]对绝缘子的损伤过程进行了试验研究,指出了应力的集中位置及损伤机制。蔡猛昌[14]对碗头挂板进行实验与数值模拟,对其进行了设计改进。还有一些学者对U型挂环、绝缘子、球头挂环及间隔棒进行了研究[15-20],为金具设计做出了贡献。这些学者大多是对单个或几个典型零件进行试验或数值模拟,判断零件的危险位置。
本文利用ABAQUS软件分别建立导线脱冰模型和耐张串金具整体模型。首先,验证导线脱冰模拟的准确性。然后,研究六分裂导线发生不同步脱冰时各子导线的张力情况和导线束扭转角的变化规律。最后,选取不同时刻子导线的张力加载到耐张串金具的有限元模型上,计算分析耐张串金具在导线脱冰过程中的应力及其分布情况。
1 输电线脱冰模拟分析
1.1 输电线覆冰脱落的模拟方法
模拟导线脱冰试验中,要实现导线均匀覆冰且覆冰同时脱落极难实现,很多学者[4-7]都采用悬挂若干集中载荷的方法来模拟导线覆冰,再以某种方法撤去集中载荷来实现覆冰脱落。本文利用Python语言在ABAQUS中建立抛物线形的导线脱冰模型,模拟导线均匀覆冰及覆冰同时脱落。考虑到输电导线是典型的悬索结构,具备受拉不受压的力学特性,对其采用三维桁架单元(T3D2)。
设计均匀覆冰导线的覆冰静荷载,采用改变密度法[12]来实现,即:让覆冰导线的惯性加速度为(9.8 m/s2),为确保覆冰导线在任意位置的惯性力均等于“导线自重+覆冰荷载”,赋予未脱落档覆冰导线等效密度为
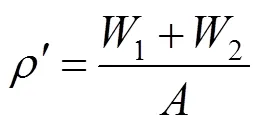
其中,1为单位长度导线质量(kg/m);2为单位长度导线覆冰重量(kg/m);为导线的横截面积。
均匀覆冰导线的脱冰荷载,将其视为体积力,通过改变输电线覆冰脱落前后的惯性加速度来实现覆冰脱落[12],即:分别赋予脱落档覆冰导线脱冰前后的惯性加速度为ʹ和(9.8 m/s2)。为了不改变脱冰前覆冰导线的惯性力,赋予脱落档覆冰导线等效密度为
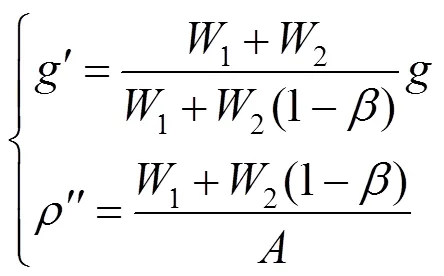
其中,1,2和的含义同式(1);为脱冰档导线的脱冰率。
导线的单位长度覆冰质量可根据覆冰厚度及导线的物理参数计算得到,计算式[12]如下

其中,为覆冰厚度(mm);为输电线外径(mm);ρ为冰的密度900 kg/m3;单位长度覆冰质量。
为验证本文导线脱冰模型的正确性,本文对文献[7]中的孤立档100%脱冰工况进行了计算。图1和表1为本文与文献[7]中孤立档跨中导线动张力的比较,可见三者的波动情况基本一致。考虑到文献[7]中客观存在的试验条件和测量误差,以及抛物线形与悬链线形导线模型的差异,表1中的误差比较理想。因此可以认为,本文的抛物线形导线模型和模拟方法是可行的。
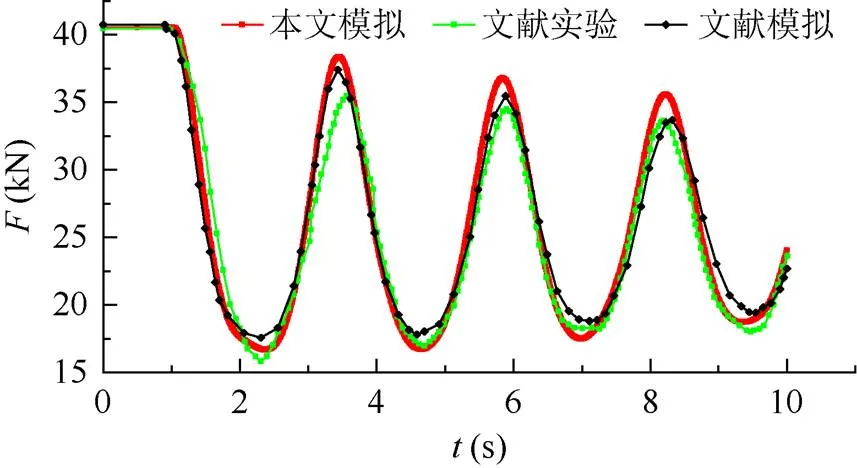
图1 本文与文献[7]脱冰响应时程曲线对比

表1 本文与文献[7]的导线动张力结果对比
(注:表中误差1=(|本文仿真值−文献试验值|/文献试验值)×100%;误差2=(|本文仿真值−文献仿真值| /文献仿真值)×100%)
1.2 六分裂导线-间隔棒有限元模型
以某特高压线路中的孤立档六分裂导线为研究对象,脱冰计算模型档距300 m,如图2所示,将子导线标记为c1~c6。假设分裂子导线处于无横风状态,两端无高差,覆冰厚度15 mm,脱冰率100%,脱冰时间为30 s。按照工程设计,将导线覆冰前初始张力设计为20%的计算拉断力。
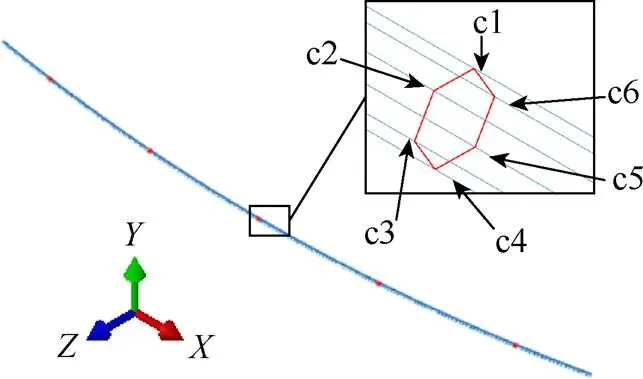
图2 六分裂导线-间隔棒有限元模型
图2中的正多边形结构是分裂导线中常用来固定子导线的间隔棒。本文采用空间梁单元(B31)对其模拟,间隔棒节点与相应的导线节点进行绑定。图2模型中的导线选用型号为JL/G1A-400/35钢芯铝绞线,其截面总面积为425.24 mm2,外径为26.8 mm,单位长度质量为1.347 5 kg/m,弹性模量为65 GPa,泊松比为0.3,计算拉断力为103.67 kN。
1.3 脱冰工况的选择及模拟结果
实际的导线脱冰是一个复杂的过程,具有随机性,多为不同步脱冰模式[11]。根据文献[11]的研究,可知,图2导线模型中的2、3、4号子导线或1、5、6号子导线同时脱冰,其余子导线仍然保留覆冰时,导线束受到的不对称载荷最大,导线束在脱冰跳跃过程中的扭转程度最严重,对线路系统的稳定性危害最大。因此,本文选择计算2,3,4号子导线同时脱冰条件下的导线动张力。
上述脱冰条件下,各子导线端部悬点的张力时程如图3所示。脱冰前,各子导线覆冰静态张力均为48.074 kN。图3中,c1~c6子导线的最大动张力依次为48.899 kN、45.770 kN、44.955 kN、45.849 kN、48.225 kN、49.956 kN,最小动张力依次为38.755 kN、32.527 kN、25.2 kN、23.519 kN、30.207 kN、37.601 kN,稳态张力(=31 s)依次为43.061 kN、37.094 kN、32.487 kN、33.462 kN、39.444 kN、43.924 kN。其中,未脱冰子导线最大动张力均大于子导线覆冰静态张力。因此,在分裂导线的不同步脱冰跳跃研究中,建议将未脱冰子导线当成重点进行分析,以满足分裂导线的强度设计要求。
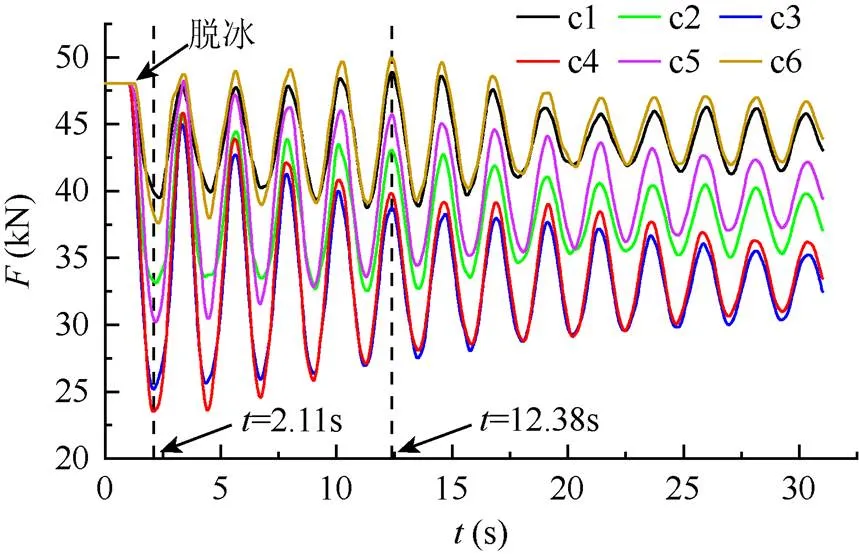
图3 子导线的张力时程
为了直观地看出导线张力与间隔棒的转角关系,本文将1号子导线端部悬点前15 s的张力时程曲线及相应的导线束中点截面内间隔棒的转角时程曲线绘制于图4。可知,间隔棒的转角大体上与导线动张力呈负相关关系,即导线张力越小,间隔棒转角越大。根据间隔棒与导线的约束关系及分裂导线与耐张串的实际安装情况,可知,导线张力越小,导线束的转角越大,耐张串承受的扭矩越大。
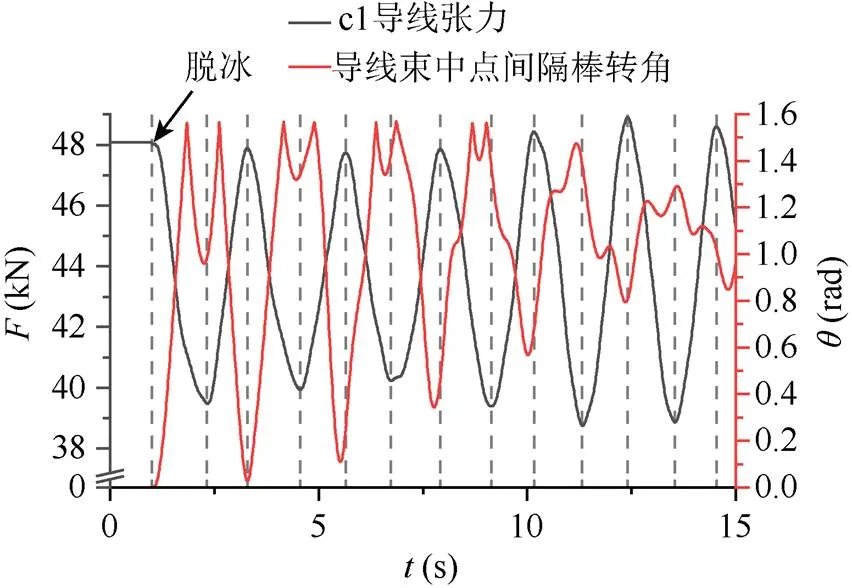
图4 c1导线的张力时程与间隔棒的转角时程
2 耐张串金具受力分析
2.1 三维实体模型
以550 kN盘形悬式绝缘子四联双挂点耐张串(8N42-50100-55P)为本文的耐张串金具模型。由于其由多个绝缘子悬挂组装成,在实际工作中,绝缘子串处于极度绷紧状态,又因金具之间的巨大静摩擦力,绝缘子几乎不会发生相对转动。鉴于本文主要探究连接金具的应力分布,故采用一根简单的圆杆来模拟绝缘子串。模型中螺栓螺纹对整体结构机械强度的影响极小,因此,省略螺纹,将螺栓变成普通的圆柱状。按照耐张串装配图组装各零件得到图5所示的耐张串计算模型。耐张串计算模型中各零件采用的材料型号见表2,螺栓的材料统一使用Q235-B。
2.2 材料特性
由于金具的几何模型采用的长度单位是mm,为了保证量纲的统一,选用的各零件材料参数见表3。钢材的本构模型选用线性强化弹塑性模型,屈服之后的切性模量为屈服之前弹性模量的1%。
2.3 模型网格划分及连接方式
为了提高计算精度,各零件尽可能采用八节点线性六面体单元(C3D8R),仅有碗头挂板采用质量较差的十节点二次四面体单元(C3D10),如图6所示。模型共有节点469 969个,308 496个六面体单元,32 040个四面体单元。网格分析检查显示,各零件单元均无分析错误提示,少数零件的单元存在分析警告提示,在单元总数的占比均不超过5%。
由于模型中共109个零件,零件之间存在相互转动,如果用接触来定义零件之间的相互作用关系将会导致模型计算难以收敛,因此本文采用ABAQUS中的多体分析方法来建立零件之间的连接关系。针对耐张串中大量形如“挂点金具-螺栓-U型挂环”(存在1个相对转动方向)与少部分形如“U型挂环-U型挂环”(存在2个相对转动方向)的连接关系,结合实际安装情况,分别采用“Hinge”和“Join+Universal”的连接方式,如图7所示。

图5 耐张串有限元模型

表2 组装零件表

表3 模型中零件的材料属性

图6 零件网格情况
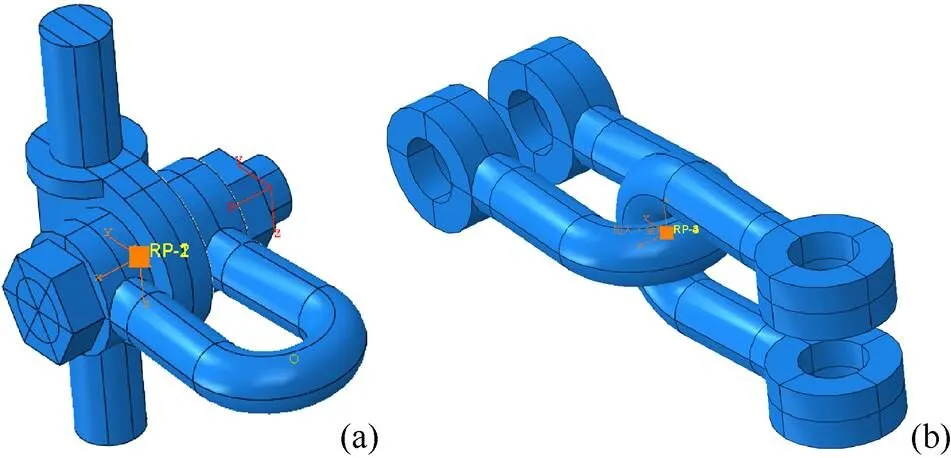
图7 零件链接关系((a)“Hinge”连接;(b)“Join+Universal”连接)
2.4 载荷及边界条件的施加
根据耐张串与分裂导线的实际安装情况,可知零件15和17为导线端部张力的直接受力构件,其与各子导线的具体连接位置如图8所示。

图8 分裂子导线在金具的连接位置
因为导线脱冰模型与耐张串金具模型是分开建立的,所以需要先根据子导线端点所在单元的2个节点坐标,求解子导线在图2中,,等3个坐标轴方向的等效张力Fʹ,Fʹ,Fʹ,然后根据图2与图8中坐标轴的对应关系,得到各子导线在图8中的等效张力F,F,F。
无人工干预时,覆冰导线常处于静态平衡状态,因此对耐张串承载导线覆冰静态张力时的受力分析是有必要的。图9为施加到耐张串上的子导线等效张力F,F,F,最大动张力和最小动张力分别是图3中6号子导线取最大动张力(=2.11 s)时的张力数值和4号子导线取最小动张力(=12.38 s)时的张力数值。根据图9可知,导线覆冰静态张力>导线最大动张力>导线稳态张力>导线最小动张力。考虑耐张串的实际安装情况,约束零件1在,,等3个方向的位移。

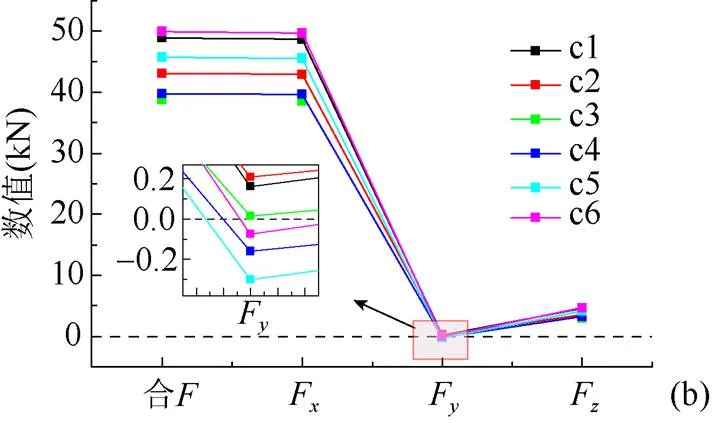


图9 耐张串的载荷工况((a)覆冰静态张力; (b)最大动张力;(c)最小动张力;(d)稳态张力)
3 耐张串计算结果与讨论
3.1 耐张串的应力场分析
耐张串在图9(a)所示的载荷工况下的应力云图及位移云图如图10所示。耐张串的位移云图见图10中的右上图(阴影网格部分为耐张串初始状态),由于零件之间存在巨大的相互作用力,耐张串整体就像一根绷紧的链条,上下U形挂环之间发生的微小转动,使得耐张串U形挂环下端零件都绕着上部U形挂环发生转动,考虑到实体模型仅有3个位移方向的自由度,U形挂环下端零件的运动形式就表现为方向有明显位移,符合耐张串在图9(a)所示载荷条件下的运动,表明耐张串模型中的连接关系和边界条件是正确的。
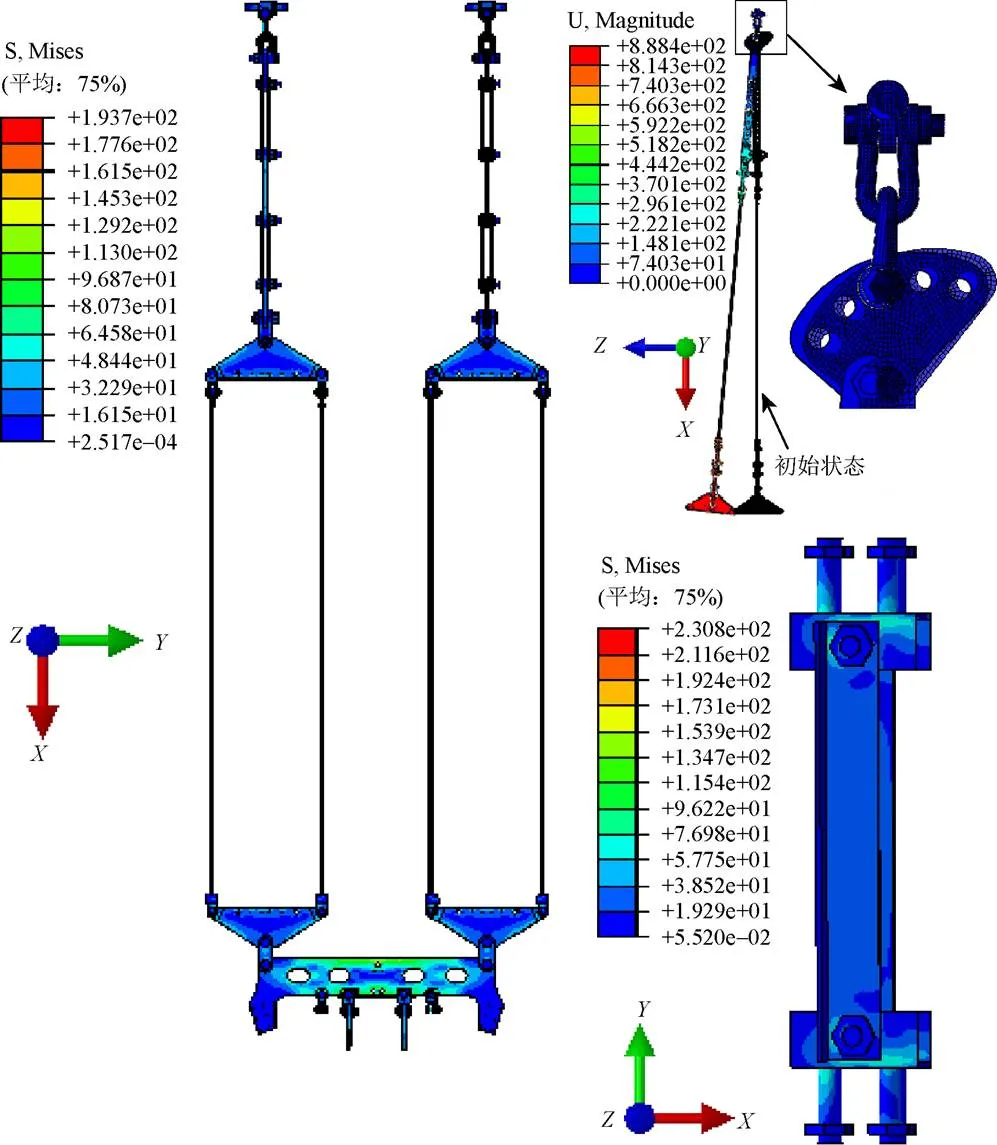
图10 导线覆冰静态条件下,耐张串的应力云图与位移云图(N/mm2)
图11(a)~(c)依次为耐张串在图9(b)~(d) 3种载荷工况下的应力云图。
观察图10中的绝缘子杆件,发现其最大应力为130.3 MPa。所以,图10和图11中去除绝缘子杆件、支撑架及装配在上面的螺栓后,耐张串依次在图9中4种载荷工况下的应力最大值为193.7 MPa,176.5 MPa,125.5 MPa,151.8 MPa,可知耐张串承载导线最小动张力与稳态张力时的应力最大值跨度为68.2 MPa。又由于实际的分裂导线脱冰跳跃时间常只有几十秒,且导线张力是衰减往复变化,这使得耐张串在导线脱冰过程中一定存在不稳定交变应力,最终可使得各零件产生疲劳损坏。
3.2 零件的应力应变分析
图12(a)~(d)依次为支撑架在耐张串承载图9(a)~ (d)所示4种导线张力时的应力云图可知,支撑架在17号联板承载导线动荷载时,发生了不同程度的扭曲变形,符合17号联板承载图9所示载荷时,支撑架的变形运动。结合图9所示4种导线张力的大小判断,可知,导线张力越小,支撑架应力越大。
根据图10~图12可知,4种载荷工况下,耐张串的应力最大值出现在支撑架或与支撑架绑定的螺栓上。考虑到材料的屈服强度,可知,耐张串在实际的导线脱冰跳跃过程中多数零件都处于弹性变形阶段,不存在塑性应变,都可视为安全。计算结果中仅有与支撑架绑定的螺栓和图12(c)所示的支撑架的应力最大值超过了其对应材料的屈服强度,图12(c)所示的支撑架的等效塑性应变结果如图13所示,绑定在支撑架上的螺栓的等效塑性应变结果如图14所示。

图13 支撑架的等效塑性应变云图
从图13和图14可发现,支撑架及与其绑定的螺栓的塑性应变最大值为0.006 801(长度mm)。理想条件下,支撑架及与其绑定的螺栓是安全的,但当考虑模型加工工艺及材料的空隙缺陷时,支撑架及与其绑定的螺栓可能发生破坏,进而影响整个输电线系统的安全性能。对此,建议不同零件的连接螺栓采用强度不同的材料,支撑架可以根据实际需求增加厚度或改用强度更高的材料,以满足耐张串金具在实际应用中的强度要求。

图14 绑定在支撑架上螺栓的等效塑性应变云图((a)覆冰静态张力;(b)最大动张力;(c)最小动张力;(d)稳态张力)
其余零件在图9所示的载荷工况下的应力分布、应力最大值位置几乎完全一致,应力的大小关系均为:导线覆冰静态张力>导线最大动张力>导线稳态张力>导线最小动张力。因此,后文除17号联板外均只展示零件在导线覆冰静态载荷下的应力云图。
根据图9所示4种导线张力的大小判断及耐张串在图9所示载荷工况下,各零件的应力大小关系,可知,导线张力越小,支撑架应力越大,其余零件的应力越小。结合1.3节导线张力与耐张串所受扭矩的关系判断:支撑架是扭矩的主要受力构件,其余零件主要承载导线的纵向张力(图9中的F),受扭矩的影响较小。因此,关于耐张串金具的受力分析研究,建议根据各零件的主要受力形式,将承载子导线最大动张力和最小动张力加以区别分析,以满足零件的强度设计要求。
图15(a)~(d)依次为17号联板承载图9所示的覆冰静态张力、最大动张力、最小动张力和稳态张力时的应力云图,可知,联板的应力分布情况几乎一致,在施加载荷的圆孔区域和联板由厚变薄的连接区域存在应力集中现象。

图15 17号联板的应力云图(N/mm2)((a)覆冰静态张力; (b)最大动张力;(c)最小动张力;(d)稳态张力)
图16(a)和(b)依次为与挂点金具连接的U型挂环和与调整板连接的U型挂环的应力云图。根据图16(b)可知,U型环与杆部的连接处发生应力集中,而挂环U型区域的最低点未发生应力集中,则是因为图中黑框部分与参考点创建了无位移、无转动的耦合,使得耦合区域刚化。
图16(a)中的U型挂环存在左右两侧应力相差极大的现象,其原因与耐张串受力后的运动有关。因为U型挂环之间的连接单元位于2个U型挂环的接触点,且采用“Join+Universal”的连接方式(相对平移分量1=2=3=0),所以与调整板连接的U型环发生转动时必然会远离与挂点金具连接的U型挂环的一侧内壁、并压迫另一侧内壁,造成与挂点金具连接的U型挂环一侧内壁应力减小、而另一侧内壁应力增大。图17展示了2个U型挂环在相对转动过程中的应力变化,与分析一致。根据图17,可知,U型挂环相对转角的大小与应力最大值非正相关关系,建议设计U型挂环时要考虑U型环之间不同相对转角下的结构强度。

图16 U型挂环的应力云图(N/mm2)((a)连接挂点金具的U型挂环;(b)连接调整板的U型挂环)
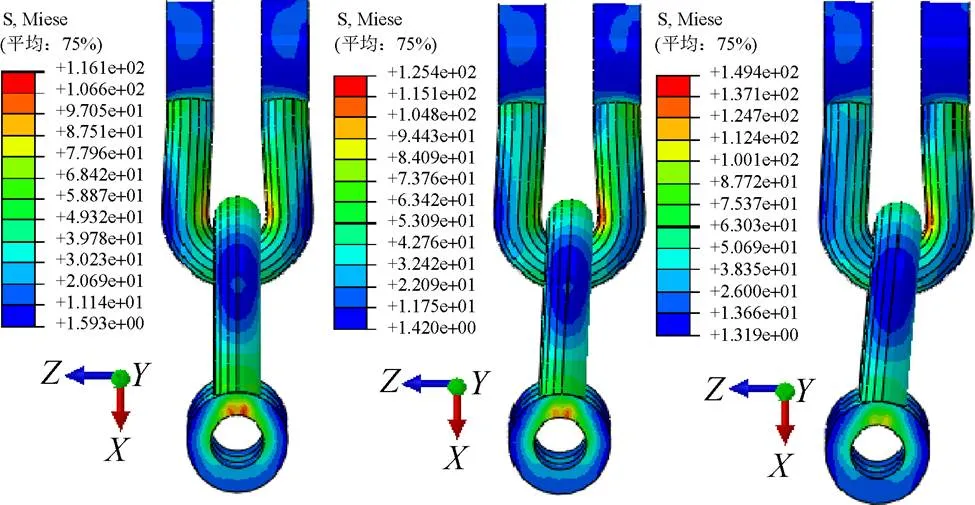
图17 U型挂环相对转动过程的应力云图(N/mm2)
耐张串承载导线覆冰静态张力时,球头挂环的应力云图如图18所示。应力最大值出现在挂环与杆部的过渡位置,表明此处为易断裂位置,与文献[19]中球头挂环的断裂位置吻合(图19)。

图18 球头挂环的应力云图(N/mm2)

图19 文献[19]中的球头挂环断裂情况(N/mm2)
图20为LT4联板在耐张串承载导线覆冰静态张力时的应力云图,可知,其中段边缘处的应力值大,左右两边连接13号挂板的圆孔附近的应力值小。前文分析可知耐张串承载导线覆冰静态张力时,LT4联板的应力最高,建议设计时重点考虑其在导线静态平衡下的强度要求,但不可忽略所用材料的疲劳性能。

图20 LT4联板的应力云图(N/mm2)
图21为耐张串承载导线覆冰静态张力时,圆孔与参考点耦合的各零件的应力云图。参考点与零件圆孔进行的是无位移、无转动的耦合方式,使得零件圆孔形成了刚化效应,进而导致圆孔附近的应力不够准确,但对零件其他位置应力分布影响不大。从应力云图中可以预估零件的危险位置,进而改进零件形状,增强其结构强度。
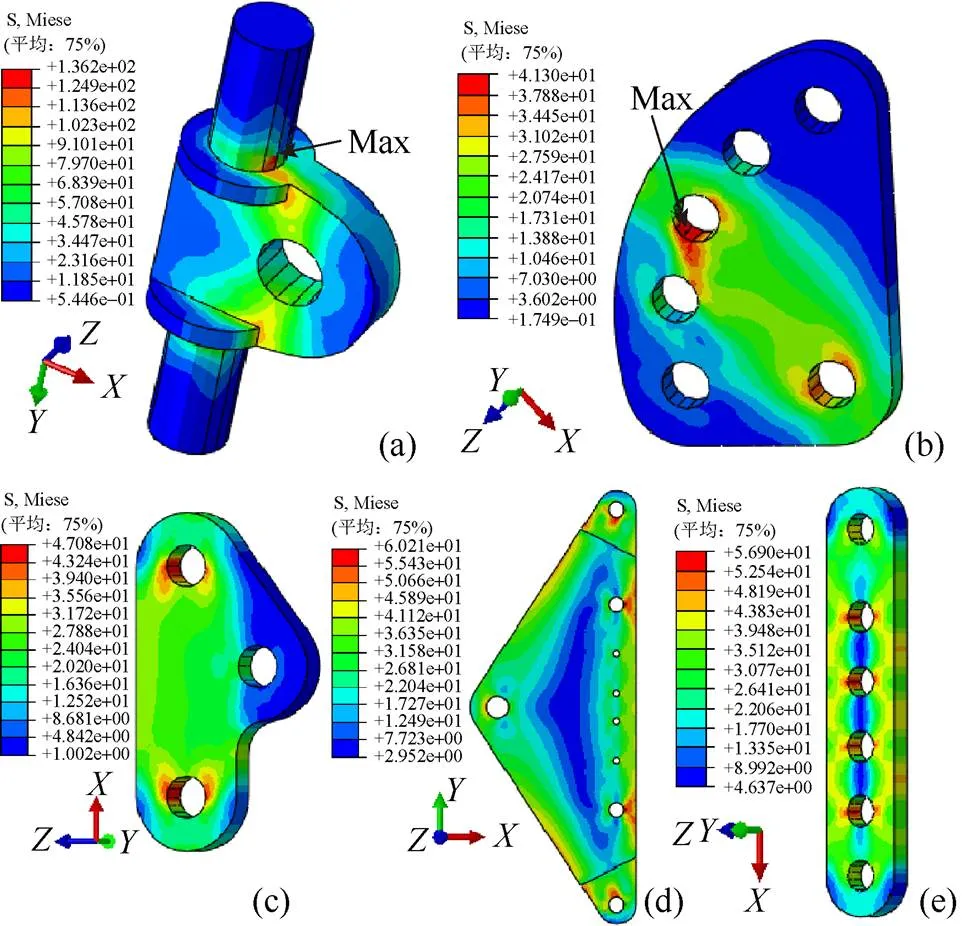
图21 圆孔与参考点耦合零件的应力云图(N/mm2)
图22为耐张串承载导线覆冰静态张力时,与螺栓建立绑定约束的各零件的应力云图。由于零件与螺栓为表面-表面绑定方式,可知零件中圆孔区域有相当多的节点与螺栓的节点是绑定约束关系,导致圆孔区域的多数节点之间的相对位移很小,进而使得圆孔区域的应力减小。根据圣维南原理局部的约束方式,虽然圆孔绑定区域的应力值不够准确,但对零件其他区域的应力分布影响不大,故仍可从这些云图中预估零件其它位置的应力值,探寻零件其它位置的危险情况。
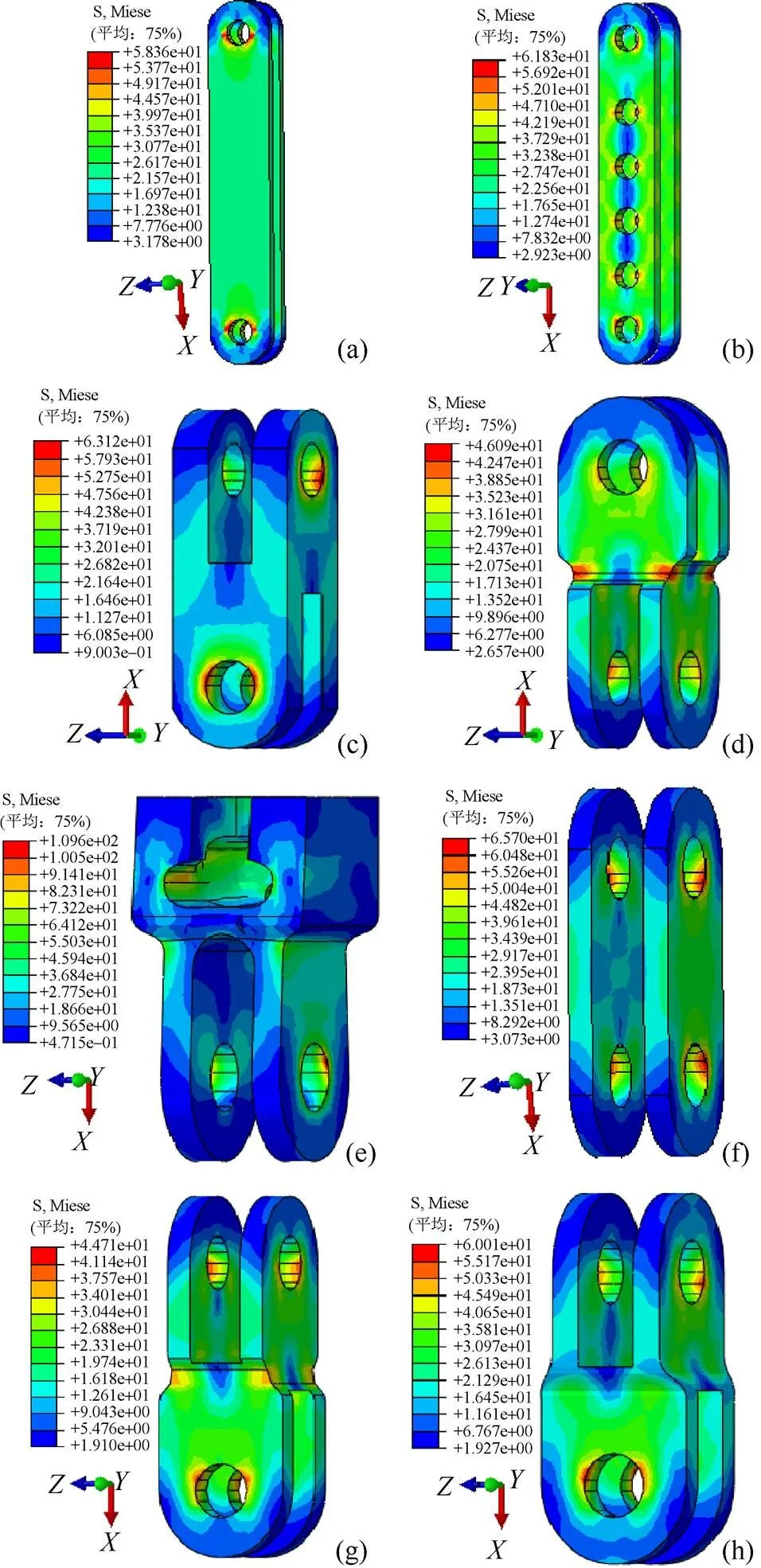
图22 与螺栓建立绑定约束零件的应力云图(N/mm2)
4 结 论
(1) 耐张串分别承载导线覆冰静态张力、最大动张力、最小动张力和稳态张力时的计算结果显示:支撑架及绑定在支撑架上的螺栓的应力最大值超过了材料的屈服强度。建议不同零件的连接螺栓采用强度不同的材料,支撑架根据实际需求增加厚度或改用更高强度的材料,以满足耐张串金具在实际应用中的强度要求。
(2) 分裂导线不同步脱冰时,支撑架是扭矩的主要受力构件,其余零件主要承载导线的纵向张力,受扭矩的影响较小。关于耐张串金具的受力分析研究,建议根据各零件的主要受力形式,将承载子导线最大动张力和最小动张力加以区别分析,以满足零件的强度设计要求。
(3) 分析了部分连接金具的应力分布,标记了连接金具的危险位置,并发现U型挂环之间的相对转角与其应力最大值不属于线性关系,设计U型挂环时,建议考虑U型挂环不同转角下的结构强度。
(4) 展示了输电线耐张串各连接金具的应力云图,对连接金具的设计改进有一定的参考意义。
[1] 王传辉, 姚叶青, 夏令志, 等. 2018年初安徽省沿江地区输电线路舞动天气成因分析[J]. 高原气象, 2019, 38(5): 1091-1098. WANG C H, YAO Y Q, XIA L Z, et al. Cause of the galloping in Anhui Province along the Yangtze River in early 2018[J]. Plateau Meteorology, 2019, 38(5): 1091-1098 (in Chinese).
[2] 王津宇, 李哲, 刘善峰, 等. 基于风险系数的输电线路覆冰舞动预警方法[J]. 高压电器, 2019, 55(9): 194-199. WANG J Y, LI Z, LIU S F, et al. Early warning method of iced transmission line galloping based on risk coefficient[J]. High Voltage Apparatus, 2019, 55(9): 194-199 (in Chinese).
[3] 胡毅, 刘凯, 吴田, 等. 输电线路运行安全影响因素分析及防治措施[J]. 高电压技术, 2014, 40(11): 3491-3499. HU Y, LIU K, WU T, et al. Analysis of influential factors on operation safety of transmission line and countermeasures[J]. High Voltage Engineering, 2014, 40(11): 3491-3499 (in Chinese).
[4] MORGAN V T, SWIFT D A. Jump height of overhead-line conductors after the sudden release of ice loads[J]. Proceedings of the Institution of Electrical Engineers, 1964, 111(10): 1736-1746.
[5] 王璋奇, 齐立忠, 杨文刚, 等. 集中质量法模拟覆冰在架空线脱冰动张力实验中的适用性研究[J]. 中国电机工程学报, 2014, 34(12): 1982-1988. WANG Z Q, QI L Z, YANG W G, et al. Research on the applicability of lumped mass method for cable’s dynamic tension in the ice shedding experiment[J]. Proceedings of the CSEE, 2014, 34(12): 1982-1988 (in Chinese).
[6] 李宏男, 吴育炎. 输电线路覆冰脱落动力效应试验研究[J]. 土木工程学报, 2019, 52(5): 35-46,100. LI H N, WU Y Y. Experimental study on dynamic responses of transmission lines caused by ice shedding[J]. China Civil Engineering Journal, 2019, 52(5): 35-46,100 (in Chinese).
[7] 陈勇, 胡伟, 王黎明, 等. 覆冰导线脱冰跳跃特性研究[J]. 中国电机工程学报, 2009, 29(28): 115-121. CHEN Y, HU W, WANG L M, et al. Research on ice-shedding characteristic of icing conductor[J]. Proceedings of the CSEE, 2009, 29(28): 115-121 (in Chinese).
[8] JAMALEDDINE A, MCCLURE G, ROUSSELET J, et al. Simulation of ice-shedding on electrical transmission lines using adina[J]. Computers & Structures, 1993, 47(4-5): 523-536.
[9] KOLLAR L E, FARZANEH M. Vibration of bundled conductors following ice shedding[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 1097-1104.
[10] 黄新波, 徐冠华, 肖渊, 等. 输电线路档距组合对覆冰导线脱冰跳跃的影响[J]. 高电压技术, 2015, 41(7): 2356-2361. HUANG X B, XU G H, XIAO Y, et al. Impact of transmission line span combination on ice-shedding of iced conductor[J]. High Voltage Engineering, 2015, 41(7): 2356-2361 (in Chinese).
[11] 董永星, 武怡帆, 芮晓明, 等. 分裂导线不同步脱冰动力响应研究[J]. 华北电力大学学报: 自然科学版, 2018, 45(1): 86-91,100. DONG Y X, WU Y F, RUI X M, et al. Research on dynamic response of bundled conductor after non-synchronous ice shedding[J]. Journal of North China Electric Power University: Natural Science Edition, 2018, 45(1): 86-91,100 (in Chinese).
[12] 陈科全. 覆冰输电线路脱冰动力响应及机械式除冰方法研究[D]. 重庆: 重庆大学, 2012. CHEN K Q. Study on dynamic responses of iced transmission line after ice-shedding and the mechanical de-icing method[D]. Chongqing: Chongqing University, 2012 (in Chinese).
[13] PRENLELOUP A, GMÜR T, BOTSIS J, et al. Stress and failure analysis of crimped metal-composite joints used in electrical insulators subjected to bending[J]. Composites Part A: Applied Science and Manufacturing, 2009, 40(5): 644-652.
[14] 蔡猛昌. 基于有限元的新型碗头挂板分析与研究[D]. 扬州: 扬州大学, 2014. CAI M C. Analysis and research of new type bowl head hanging plate based on finite element method [D]. Yangzhou: Yangzhou University, 2014 (in Chinese).
[15] 刘冠辰. 特高压输电线路U形挂环—调整环耐磨性能研究[D]. 北京: 华北电力大学, 2016. LIU G C. Research of the wear performance on the UHV transmission line U-rings and adjusting rings[D]. Beijing: North China Electric Power University, 2016 (in Chinese).
[16] 逯平平, 李新梅, 杨现臣. 电力金具U型环磨损后的组织与性能[J]. 热加工工艺, 2019, 48(24): 46-49, 55. LU P P, LI X M, YANG X C. Structure and performance of electric power fittings U-shaped ring after wear[J]. Hot Working Technology, 2019, 48(24): 46-49, 55 (in Chinese).
[17] 杨现臣, 李新梅. 新疆大风区输电线U型环磨损试验分析[J]. 铸造技术, 2016, 37(10): 2055-2057. YANG X C, LI X M. Analysis on wear test of power line U-shaped ring in Xinjiang wind region[J]. Foundry Technology, 2016, 37(10): 2055-2057 (in Chinese).
[18] 刘洋, 袁田, 徐偲达, 等. 静态载荷下盘形悬式绝缘子形变特性研究[J]. 电瓷避雷器, 2019(6): 198-204. LIU Y, YUAN T, XU S D, et al. Study on stress-strain characteristics of cap and pin insulator under static load[J]. Insulators and Surge Arresters, 2019(6): 198-204 (in Chinese).
[19] 韩哲文, 蒋楠, 蔡文河, 等. 输电线路连接金具疲劳断裂失效分析研究[J]. 华北电力技术, 2015(7): 44-49. HAN Z W, JIANG N, CAI W H, et al. Fatigue fracture failure of connection fittings on transmission line[J]. North China Electric Power, 2015(7): 44-49 (in Chinese).
[20] 张龙祥. 六分裂式相间间隔棒连接金具断裂分析及结构优化[D]. 太原: 太原理工大学, 2014. ZHANG L X. The fracture analysis and structural optimization of the six split interphase spacers connection fittings[D]. Taiyuan: Taiyuan University of Technology, 2014 (in Chinese).
Simulation analysis of stress in power fitting for strain insulator-string following ice shedding from cables
LI Chun1, LIU Xiao-hui1,2, HUANG Rui1, YE Zhong-fei3, WU Chuan3, ZHANG Bo3
(1. College of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China; 2. State Key Laboratory of Bridge and Tunnel Engineering in Mountain Areas, Chongqing Jiaotong University, Chongqing 400074, China; 3. Key Laboratory of Power Transmission Line Galloping Prevention and Control Technology, State Grid Henan Electric Power Research Institute, Zhengzhou Henan 450052, China)
In order to address the damaging impact on the electric power fittings of the tension change of conductors due to ice shedding from cables, the wire model of UHV transmission line and the integral model of strain insulator-string were established respectively using the ABAQUS software. Based on the method of changing density, the ice shedding from six-bundle conductors with uniform ice-coating was simulated. Under non-synchronous ice shedding conditions, research was undertaken into the dynamic tension of sub-conductors and the torsion angle of the six-bundle conductor. The results show that the maximum dynamic tension of sub-conductors without ice shedding is larger than that of the static tension of iced conductors, and that the dynamic tension of the conductor is negatively correlated with the torsion angle of the conductor bundle. Finally, the finite element analysis was conducted based on the effect of static tension of iced conductor, and the maximum dynamic tension, the minimum dynamic tension, and the steady tension of conductors caused by iced shedding on the stress of strain insulator-string. The result reveals that the changing relationship between the stress of each electric power fitting of strain insulator-string and the tension of sub-conductors is inconsistent. The failure of the electric power fittings with greater stress and the sudden shape change were analyzed separately. The research results can inform the design and optimization of electric power fittings.
ABAQUS;six bundled conductors; non-synchronous ice shedding; strain insulator-string; stress
TM 743
10.11996/JG.j.2095-302X.2021020279
A
2095-302X(2021)02-0279-10
2020-07-16;
16 July,2020;
2020-09-12
12 September,2020
国家自然科学基金项目(51308570);重庆市科委基础科学与前沿技术研究(cstc2017jcyjAX0246)
National Natural Science Foundation of China (51308570); Basic Research and Frontier Exploration Project of Chongqing China (cstc2017jcyjAX0246)
李 春(1996–),男,重庆涪陵人,硕士研究生。主要研究方向为结构动力学。E-mail:lichun023@163.com
LI Chun (1996-), male, master student. His main research interest covers dynamics of structure. E-mail:lichun023@163.com
刘小会(1981–),男,内蒙古包头人,副教授,博士。主要研究方向为输电线结构动力学分析。E-mail:cqdxlxh@126.com
LIU Xiao-hui (1981-), male, associate professor, Ph.D. His main research interest covers dynamics analysis of transmission line structure. E-mail:cqdxlxh@126.com
