可变参数的有理分形插值曲线建模
2021-05-13张欣悦雷一凡刘培培包芳勋张云峰
张欣悦,雷一凡,刘培培,包芳勋,张云峰
可变参数的有理分形插值曲线建模
张欣悦1,雷一凡1,刘培培2,包芳勋1,张云峰2
(1. 山东大学数学学院,山东 济南 250100;2. 山东财经大学计算机科学与技术学院,山东 济南 250014)
为了有效地处理复杂真实现象中的不规则数据,提出一种利用有理分形插值进行分形曲线建模的方法。首先,基于传统的具有形状参数的有理样条,构造了一类具有函数尺度因子的有理迭代函数系统,并定义了有理分形插值曲线。然后,研究了有理分形曲线的一些重要性质,包括光滑性、稳定性以及收敛性。最后,估计了有理分形曲线计盒维数的上下界。提出的可变参数的有理分形插值推广了传统的单变量有理样条,适用于拟合不规则数据或逼近具有连续但不规则导数的函数,具有更好的灵活性和多样性。数值实例和曲线建模表明,该方法不仅在视觉效果上明显优于Bézier插值,B样条插值以及基于多项式的分形插值方法,而且在均方根误差的数值对比中也具有显著优势。
有理分形插值;函数尺度因子;不规则数据;分析性质;曲线建模
由迭代函数系统(iterated function system,IFS)生成的分形插值是处理复杂真实现象中高度不规则数据的一种强大而有效的工具。目前,许多研究对分形插值曲线做出贡献。例如,文献[1-5]讨论了分形插值函数(fractal interpolation functions,FIFs)和递归分形插值函数(recursive fractal interpolation functions,RFIFs)的构造。单变量FIFs的一些重要性质已经被探讨,包括分形维数、中心变差、光滑性、稳定性和扰动误差等[6-9]。进一步的,FIFs被推广到Hermite分形插值和样条分形插值[10-12]。近年来,一些文献详细讨论了正数据、单调数据和凸数据等形状数据的保形问题[13-15]。
在以上的研究中,FIFs的垂直尺度因子仅限于常数。这种分形插值具有明显的自相似特征,很难对自相似性较小的不规则数据进行精确拟合或逼近。于是,为了有效处理复杂真实现象中的不规则数据,研究可变参数分形插值是一个重要的课题。然而,迄今为止这一问题还没有得到很好的探索,只有少数文献对此进行了研究。文献[16]给出了可变参数FIF的显式函数形式;文献[17]在普遍使用的IFS的基础上提出了一类可变参数的FIFs,并研究了FIFs的一些分析性质。本质上,以上研究均是基于多项式的带有函数尺度因子的分形函数,其生成的分形函数具有结构简单,易于计算的优点,但不够灵活。相对于多项式函数而言,有理函数能够更有效、更灵活地描述复杂的真实现象。对于具有可变尺度因子的有理分形插值已经引起了学者们的关注。文献[18]基于经典有理三次样条,提出了一类光滑有理样条分形插值函数(rational spline fractal interpolation functions,RSFIFs),很好地逼近了原始函数;文献[19]在经典的有理三次样条基础上构造了1连续的RSFIFs,实现了对分形曲线的约束和保单调;文献[20]使用具有函数尺度因子的有理IFS生成了分形插值,估计了计盒维数的上下界。目前,对于可变参数有理分形插值的研究已经成为一个重要的课题。
本文利用可变参数单变量有理FIFs构造了一种新的分形插值曲线,研究了有理FIFs的光滑性、稳定性和收敛性,并估计了有理分形曲线计盒维数的上下界。本文所研究的单变量有理插值能够提供插值对象的形状属性和导数的分形性,比现有插值方法更具灵活性和多样性。
1 分形曲线IFS

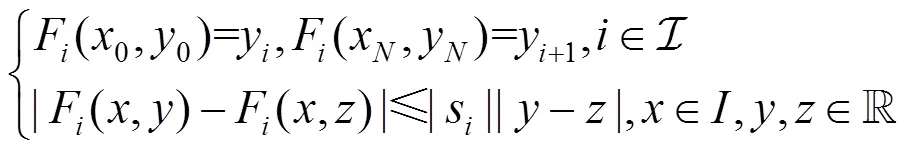
目前最常用的FIFs基于以下IFS,即
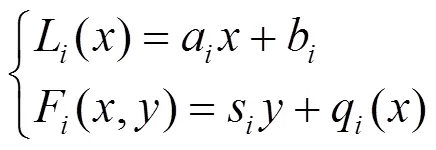
2 函数尺度因子有理分形插值曲线的构造
本文提出一种带有函数尺度因子的分形曲线。可以将这类分形曲线视为由有理扰动曲线得到的有理插值曲线的“分形扰动”。
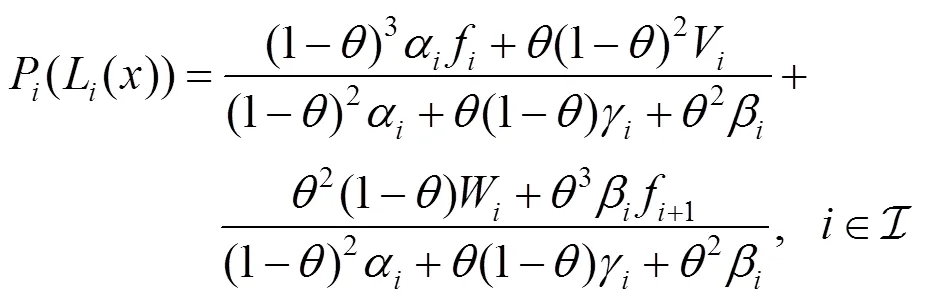
类似于式(4)的结构,扰动基函数B()可以描述为


本文在式(4)和式(5)下改进的IFS。定义

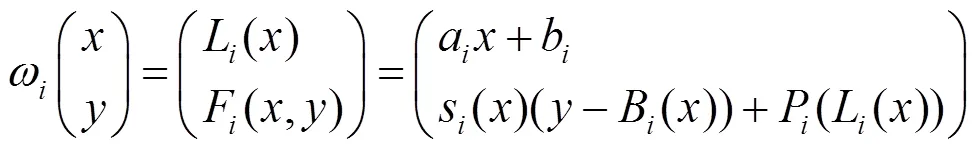
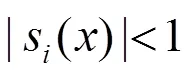

3 有理FIFs的性质
3.1 有理FIFs的光滑性

在适当的假设下,由IFS生成的有理分形曲线是光滑的,且下面的定理成立。

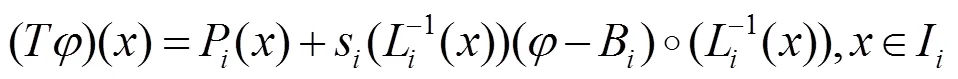

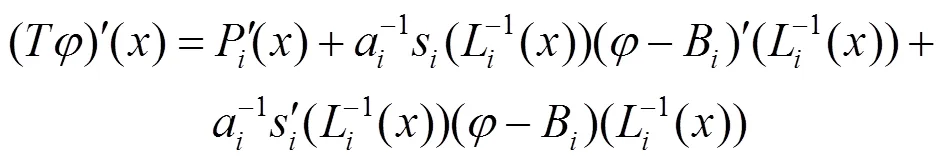
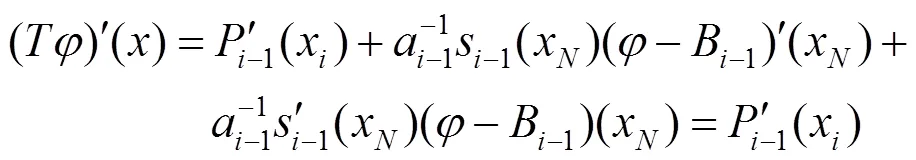
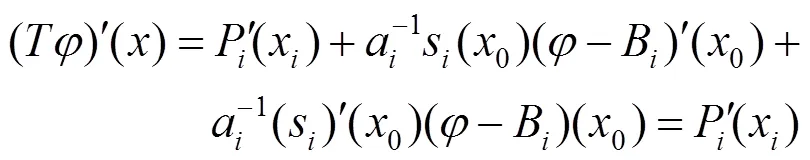
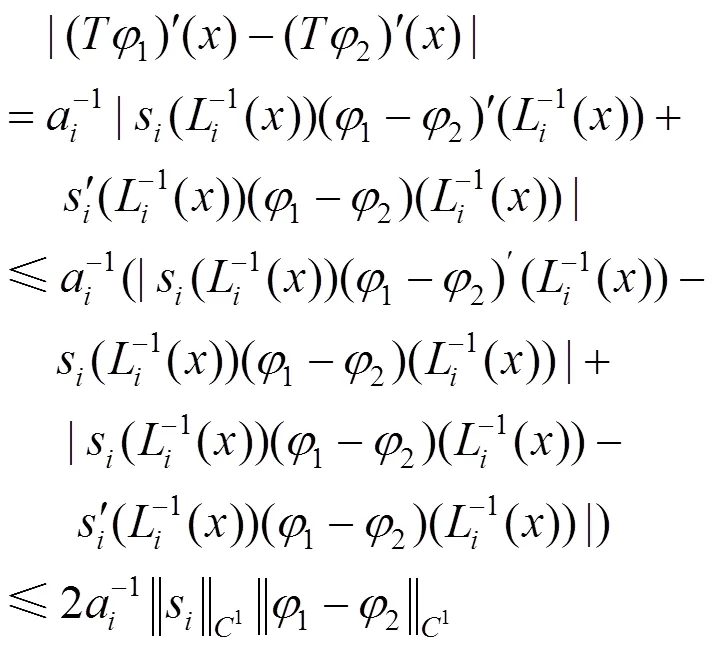
证毕。

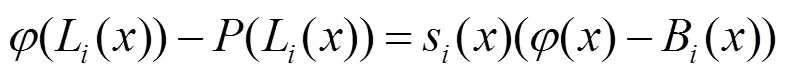
进而可得


3.2 有理分形曲线的稳定性
3.2.1 有理FIFs基函数表达式
有理FIFs基函数表达式如下
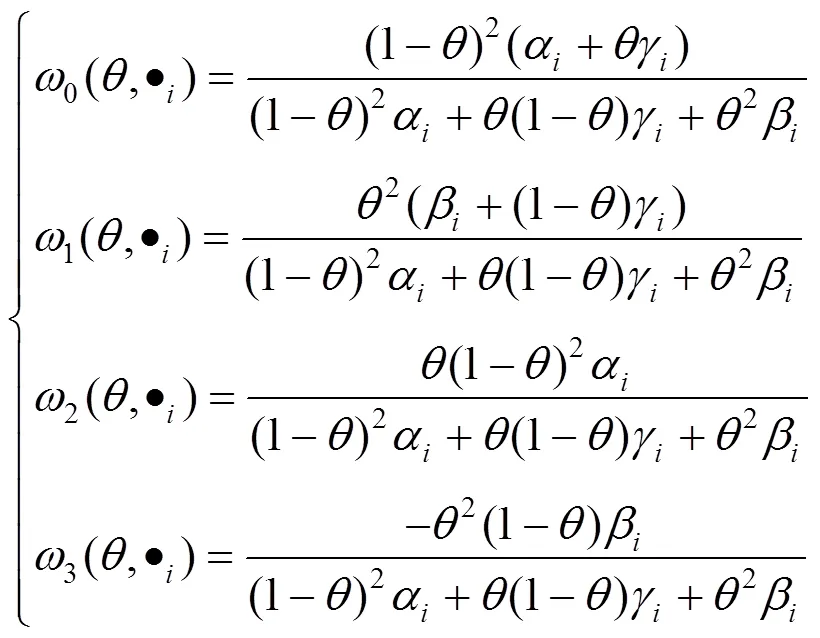
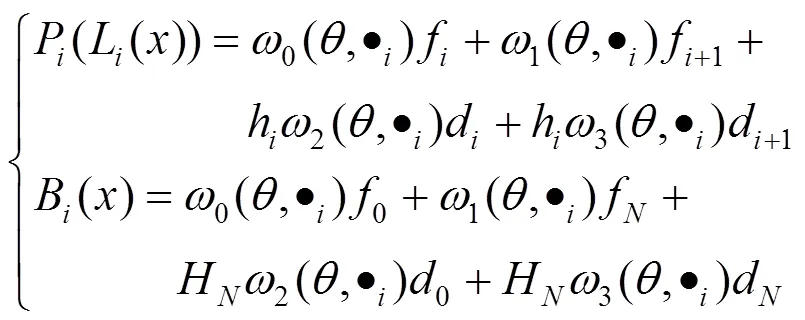
由式(20),式(16)定义的FIFs具有如下形式


3.2.2 有理FIFs稳定性分析
插值函数的稳定性是评价插值函数质量的一个重要指标,其衡量插值函数对插值数据扰动的抗干扰能力。
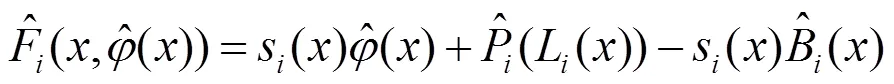

证明:由式(16)可知
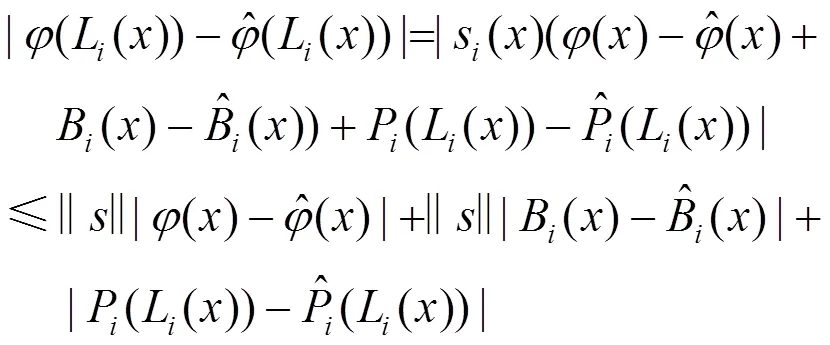
由式(20)和式(22)可得
同样有

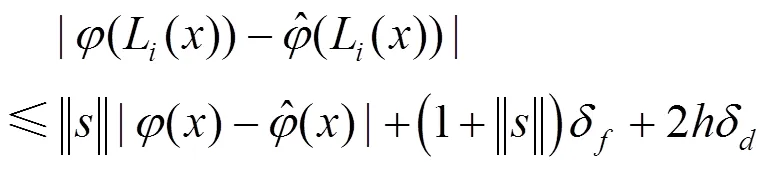
证毕。
3.3 有理FIFs的收敛性
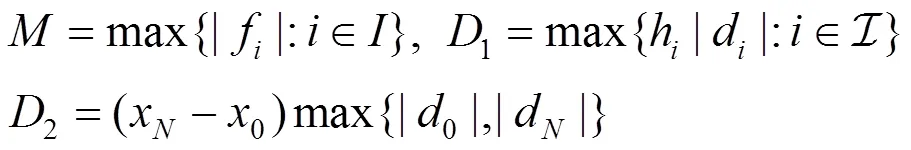
由式(20)和式(22)可得

因此,可以确定上界
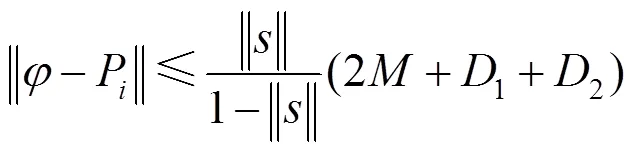
另外,通过三角不等式和式(7),有

因此,只需要讨论式(32)右边的第二个和。

根据式(33)可得
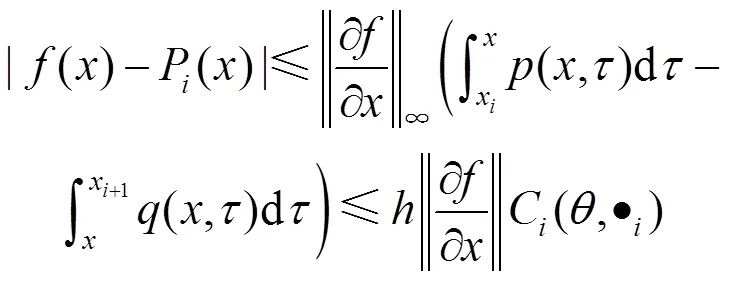

其中,

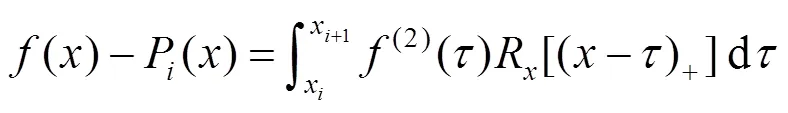
根据式(37)可得
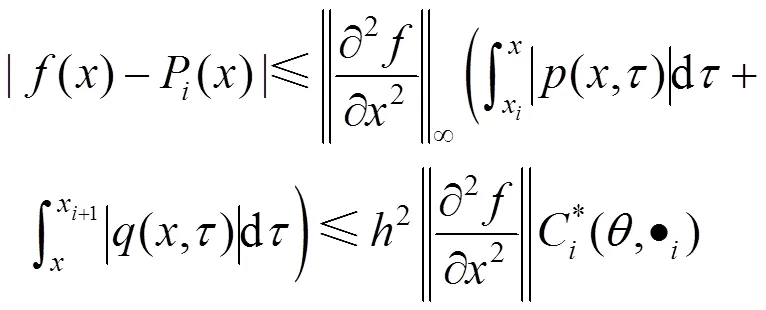
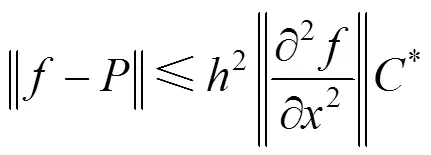
其中,

基于以上分析,可以得出定理3。
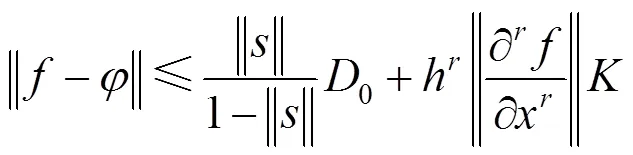
3.4 有理分形曲线的计盒维数
曲线的分形维数是曲线不规则性的度量,其描述了曲线的粗糙度。下面将研究上述有理分形曲线的计盒维数。
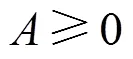
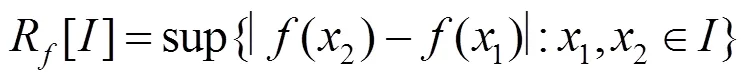

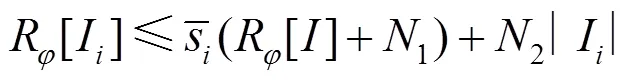
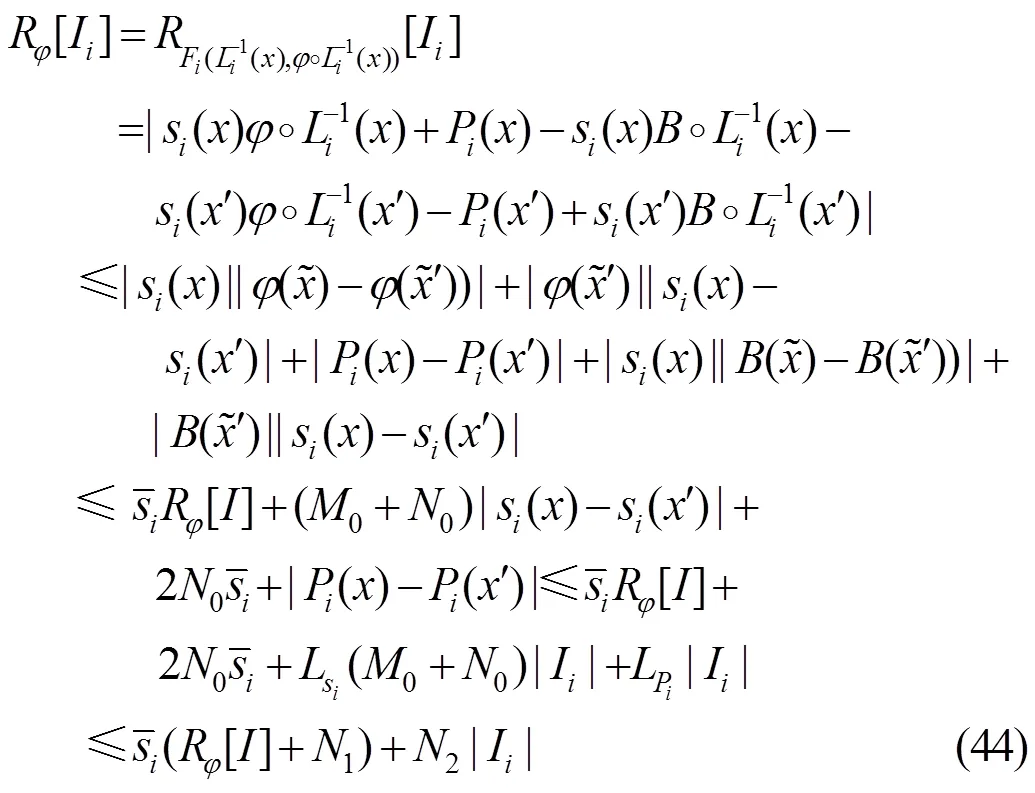


由引理2,每个区间I内的最大范围为
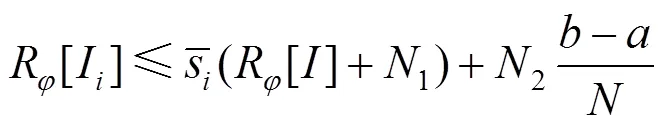

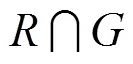


其中,
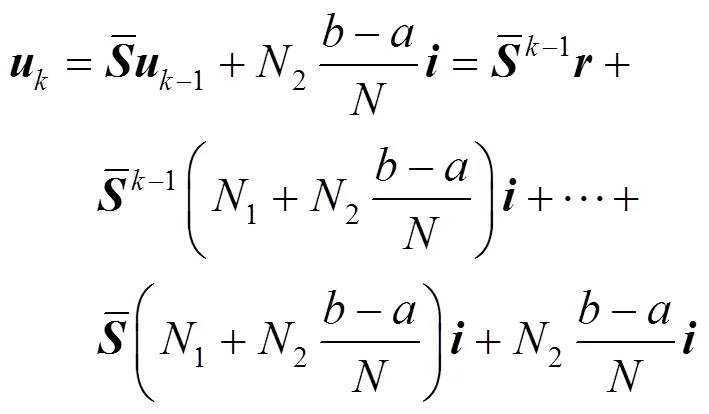
且
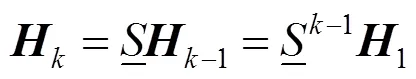
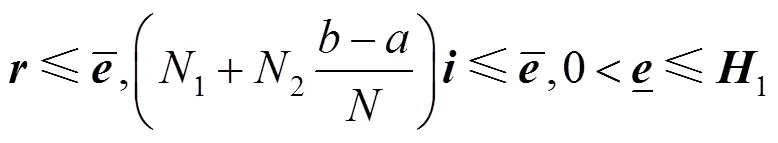
因此,根据式(49),可得

因此,可以推导出

因此

通过式(49),可得

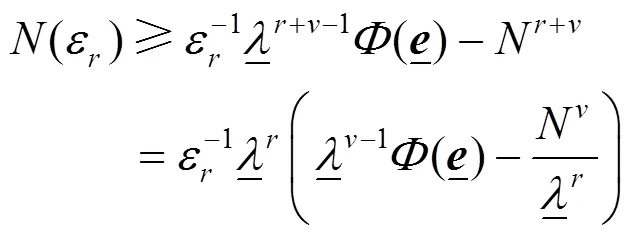
因此


证毕。
注2.当垂直尺度因子函数s()为常数s时,吸引子的计盒维数如下:
4 数值实例和曲线建模
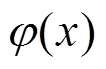
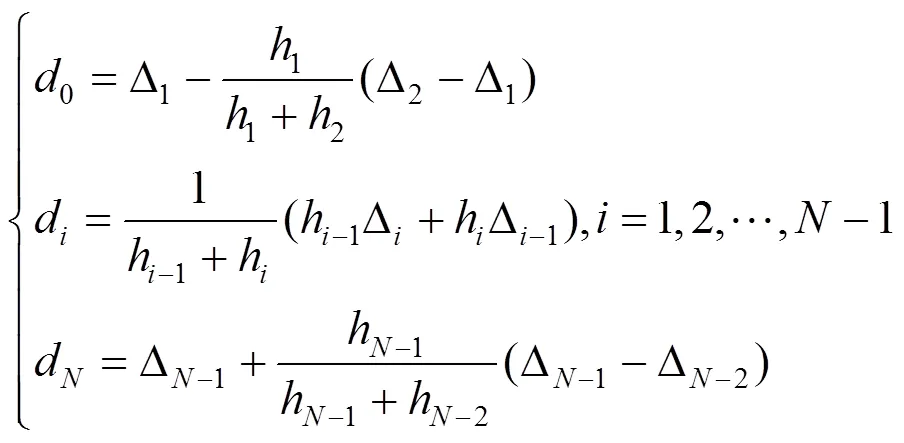
4.1 数值实例
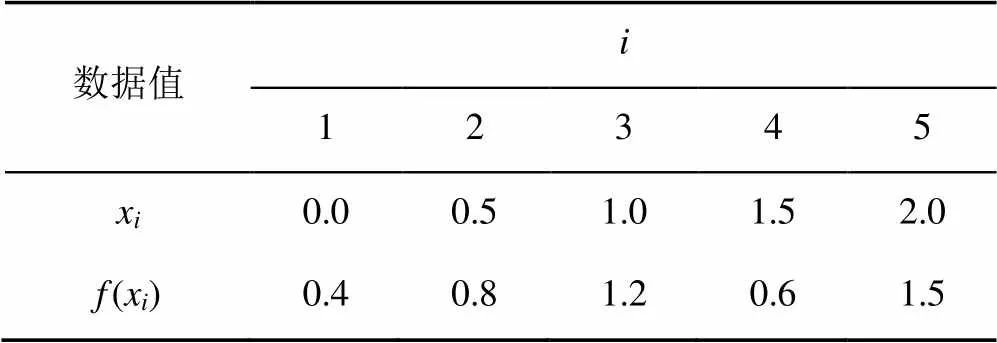
表1 插值数据

表2 表1的扰动数据
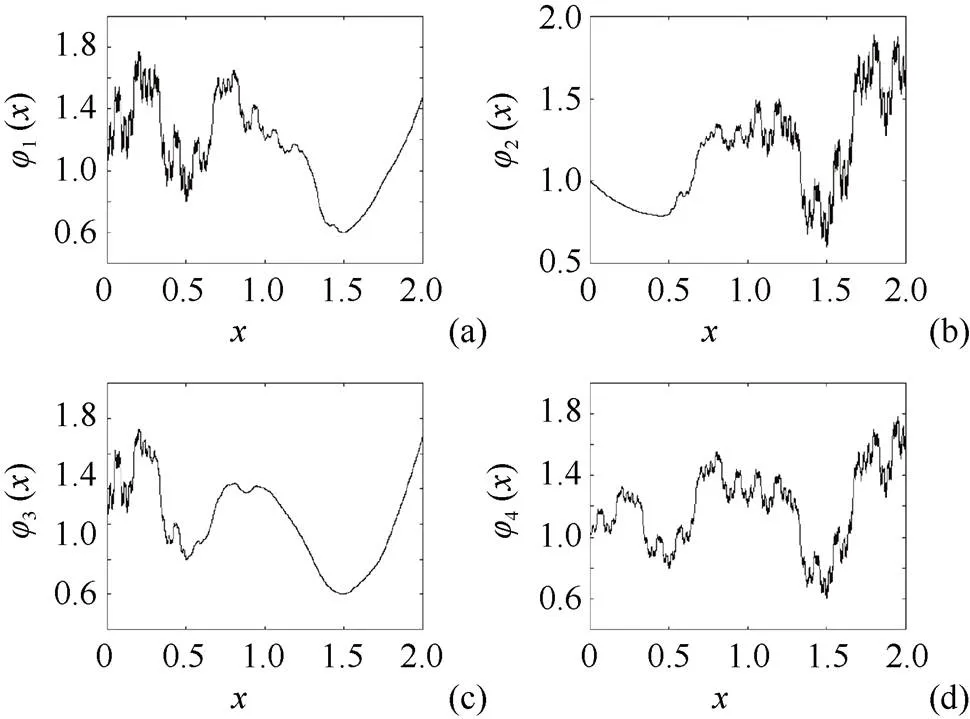
图1 具有不同函数标度因子的有理分形曲线((a)分形曲线j1(x);(b)分形曲线j2(x);(c)分形曲线j3(x);(d)分形曲线j4(x))

图2 具有不同函数标度因子的光滑有理分形曲线((a)分形曲线j1(x);(b)分形曲线j2(x);(c)分形曲线j3(x);(d)分形曲线j4(x))
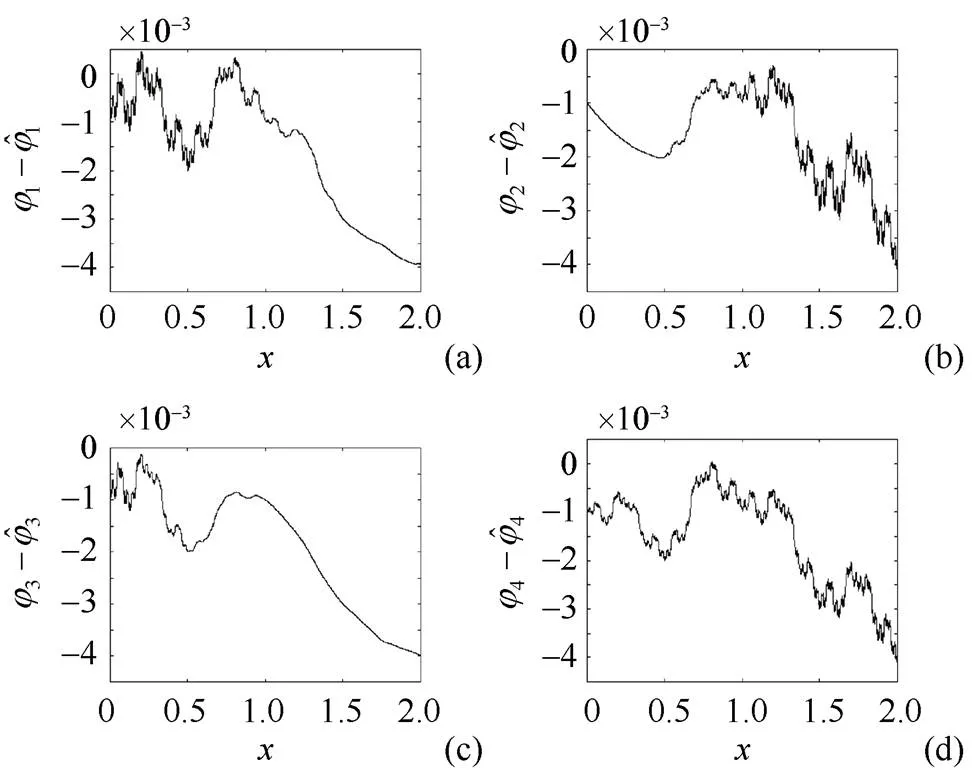
图3 有理分形曲线在插值数据扰动下的稳定性((a)误差曲线;(b)误差曲线; (c)误差曲线;(d)误差曲线)
4.2 自然对象建模
算例中,采用有理分形插值模型拟合海岸线。本文从NOAA获取数据(北纬:5°32.88096ʹ至5°59.12388ʹ;东经:5°2.02002ʹ至5°33.25278ʹ)。图4(a)为海岸线原始曲线。图4(b),图4(c)和图4(d)分别为Bézier曲线,B样条曲线和基于多项式分形插值的曲线建模结果。图4(e)为本文提出的有理分形插值函数曲线建模结果。从图中可以看出,与其他3种方法相比,本文方法能更有效地保留局部细节。

图4 不同方法在海岸线上的比较((a)原始曲线; (b) Bézier;(c) B-spline;(d)基于多项式的分形插值; (e)本文方法)
另外,本文采用均方根误差(root mean square error,RMSE)作为真实值与拟合值的误差分析指标,其是预测值与真实值偏差的平方与观测次数比值的平方根,对误差反映敏感,能够很好地反映出测量的精密度。不同方法的误差值大小见表3。从表中可以看出,与Bézier,B样条以及基于多项式的分形插值相比,本文方法误差数值明显低于另外3种方法,进一步印证了可变参数的有理分形插值优于其他插值方法。

表3 不同方法的误差值
4.3 机翼形状建模
本文提出的有理分形插值函数不仅可以对分形数据集进行拟合与逼近,还可以描述一般数据集(当s()满足定理1的条件时,相应的FIFS是光滑的)。以用于飞机工业的机翼形状设计为例,其数据来源UIUC翼型坐标数据库。图5(a)为原始曲线,图5(b)~(d)分别为Bézier插值,B样条插值和基于多项式分形插值的曲线拟合结果,图5(e)为本文提出的可变参数的有理分形插值曲线拟合结果。图像右上方红色矩形框与右下方蓝色矩形框为局部放大图像,整体拟合图像表明,4种方法均能实现对一般数据集的拟合,但从局部细节可以看出,与本文方法对比,Bézier插值曲线拟合效果差异较大,基于多项式分形插值的曲线拟合效果光滑度相对不足,B样条插值曲线拟合效果与本文方法差异不大,说明B样条插值与本文方法在拟合简单的一般数据集时均具有良好的效果,由此看出,本文方法在对一般数据集进行拟合和逼近时具有较好的竞争力,可有效地用于曲线的几何建模。

图5 不同方法的机翼形状拟合曲线((a)原始曲线; (b) Bézier;(c) B-spline;(d)基于多项式的分形插值; (e)本文方法
5 结束语
本文提出了一种有理分形插值曲线的构造方法。在经典的有理样条插值的基础上,构造了一种具有函数尺度因子的单变量有理FIFs。所建立的有理FIFs在一定的条件下是光滑的,能够更加逼近原始函数,并且对插值数据的摄动性保持了良好的稳定性。
有理FIFs通过选择合适的IFS参数值,可以提供插值函数的形状特性和导数的分形性,相较于传统的非递归插值函数更适合逼近具有连续不规则导数的函数。此外,函数尺度因子的存在为选择合适的插值曲线提供了更多的灵活多样性。实验结果表明,本文提出的可变参数的有理分形插值曲线在处理实际问题中具有很好的应用价值。
[1] BARNSLEY M F. Fractal functions and interpolation[J]. Constructive Approximation, 1986, 2(1): 303-329.
[2] BARNSLEY M F, HARRINGTON A N. The calculus of fractal interpolation functions[J]. Journal of Approximation Theory, 1989, 57(1): 14-34.
[3] MANOUSOPOULOS P, DRAKOPOULOS V, THEOHARIS T. Curve fitting by fractal interpolation[M]//Lecture Notes in Computer Science. Heidelberg: Springer, 2008: 85-103.
[4] MANOUSOPOULOS P, DRAKOPOULOS V, THEOHARIS T. Parameter identification of 1D recurrent fractal interpolation functions with applications to imaging and signal processing[J]. Journal of Mathematical Imaging and Vision, 2011, 40(2): 162-170.
[5] RUAN H J, SHA Z, SU W Y. Counterexamples in parameter identification problem of the fractal interpolation functions[J]. Journal of Approximation Theory, 2003, 122(1): 121-128.
[6] FENG Z G, XIE H P. On stability of fractal interpolation[J]. Fractals, 1998, 6(3): 269-273.
[7] NAVASCUÉS M A, SEBASTIÁN M V. Some results of convergence of cubic spline fractal interpolation functions[J]. Fractals, 2003, 11(1): 1-7.
[8] WANG H Y, LI X J. Perturbation error analysis for fractal interpolation functions and their moments[J]. Applied Mathematics Letters, 2008, 21(5): 441-446.
[9] XU J, FENG Z G. Fractal interpolation functions on the stability of vertical scale factor[J]. International Journal of Computer Mathematics, 2012(3): 380-384.
[10] CHAND A K B, KAPOOR G P. Generalized cubic spline fractal interpolation functions[J]. SIAM Journal on Numerical Analysis, 2006, 44(2): 655-676.
[11] CHAND A K B, VISWANATHAN P. A constructive approach to cubic Hermite Fractal Interpolation Function and its constrained aspects[J]. BIT Numerical Mathematics, 2013, 53(4): 841-865.
[12] NAVASCUES M A, SEBASTIAN M V. Smooth fractal interpolation[J]. Journal of Inequalities and Applications, 2006, 2006(1): 78734.
[13] BALASUBRAMANI N. Shape preserving rational cubic fractal interpolation function[J]. Journal of Computational and Applied Mathematics, 2017, 319: 277-295.
[14] LIU J S, BAO F X. Visualization of constrained data by smooth rational fractal interpolation[J]. International Journal of Computer Mathematics, 2016, 93(9): 1524-1540.
[15] VISWANATHAN P, CHAND A K B, AGARWAL R P. Preserving convexity through rational cubic spline fractal interpolation function[J]. Journal of Computational and Applied Mathematics, 2014, 263: 262-276.
[16] SERPA C, BUESCU J. Explicitly defined fractal interpolation functions with variable parameters[J]. Chaos, Solitons & Fractals, 2015, 75: 76-83.
[17] WANG H Y. Fractal interpolation functions with variable parameters and their analytical properties[J]. Journal of Approximation Theory, 2013, 175(175): 1-18.
[18] HUSSAIN M Z, SARFRAZ M, HUSSAIN M. Visualization of constrained data by rational cubics[EB/OL]. [2020-06-03]. https://www.researchgate.net/publication/286330015_Visualization_of_constrained_data_by_rational_cubics.
[19] 孙庆华, 刘甜甜, 张云峰, 等. 有理分形插值曲线的约束和单调保持[J]. 计算机辅助设计与图形学学报, 2017, 29(11): 2037-2046. SUN Q H, LIU T T, ZHANG Y F, et al. Constrained and monotone curves derived from rational fractal interpolation[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(11): 2037-2046 (in Chinese).
[20] YUN C H, HYONG-CHOL O, CHOI H C. Construction of fractal surfaces by recurrent fractal interpolation curves[J]. Chaos, Solitons & Fractals, 2014, 66: 136-143.
[21] SCHULTZ M H, Spline analysis [EB/OL]. [2020-06-03]. https://mathscinet.ams.org/mathscinet-getitem?mr=362832.
Curve modeling using rational fractal interpolation with variable parameters
ZHANG Xin-yue1, LEI Yi-fan1, LIU Pei-pei2, BAO Fang-xun1, ZHANG Yun-feng2
(1. School of Mathematics, Shandong University, Jinan Shandong 250100, China; 2. School of Computer Science and Technology, Shandong University of Finance and Economics, Jinan Shandong 250014, China)
In order to deal with irregular data from complex real phenomena, a constructive approach to fractal curves was proposed using the rational fractal interpolation. First, based on the traditional rational spline with shape parameters, we constructed one class of rational Iterated Function Systems (IFS) with function vertical scaling factors. Rational IFSs were hyperbolic and rational fractal interpolation curves were defined. Then, some important properties of rational fractal curves were investigated, including smoothness, stability and convergence. Finally, lower and upper bounds in the box-counting dimension of rational fractal curves were estimated. The presented rational fractal interpolation with variable parameters generalized the traditional univariate rational spline, which is more suitable for fitting irregular data or approximating a function with continuous but irregular derivatives, and is more flexible and diversiform. Numerical examples and curve modeling show that this method can not only significantly outperform the Bézier interpolation, B-spline interpolation, and polynomial-based fractal interpolation methods in terms of visual effects, but also display prominent advantages in numerical comparison of root mean square errors.
rational fractal interpolation; function scaling factor; irregular data; analytical property; curve modeling
TP 391
10.11996/JG.j.2095-302X.2021020245
A
2095-302X(2021)02-0245-11
2020-09-10;
10 September,2020;
2020-10-23
23 October,2020
国家自然科学基金项目(61672018,61972227);山东省自然科学基金项目(ZR2019MF051);山东省重点研发计划(2018GGX101013)
National Natural Science Foundation of China (61672018, 61972227); Natural Science Foundation of Shandong Province (ZR2019MF051); Key Research and Development Project of Shandong Province (2018GGX101013)
张欣悦(1996-),女,河北唐山人,硕士研究生。主要研究方向为CAGD、图像处理。E-mail:812426204@qq.com
ZHANG Xin-yue (1996-), female, master student. Her main research interests cover CAGD and image processing. E-mail:812426204@qq.com
包芳勋(1968-),男,山东济南人,教授,博士。主要研究方向为函数逼近、分形、CAGD。E-mail:fxbao@sdu.edu.cn
BAO Fang-xun (1968-), male, professor, Ph.D. His main research interests cover function approximation, fractal and CAGD. E-mail:fxbao@sdu.edu.cn
