考虑旅客出行选择的高速铁路差别定价
2021-05-13宋文波
赵 鹏,宋文波,李 璐
(1.北京交通大学 交通运输学院,北京 100044;2.中国铁路成都局集团有限公司 成都北车站,四川 成都 610500;3.中铁信(北京)网络技术研究院有限公司,北京 100044)
目前同一OD间运行的不同高速铁路(以下简称“高铁”)列车,席位级别相同票价相同,不能反映列车间在运行时间、发车时段等方面存在的差异性,也无法反映旅客对不同客运产品的选择偏好,造成相同OD间高铁客运产品能力利用紧张与虚糜共存的现象,影响收益的提升。而旅客的选择偏好直接影响高铁的收益,因此,综合考虑旅客的出行选择行为对相同OD间的高铁客运产品实施差别定价对于调节供需平衡、提高客运收益具有重要意义。
针对旅客出行选择行为及铁路列车定价问题,国内外学者已经做了深入研究。文献[1]针对不同类型旅客的出行行为特征,分别构建了商务旅客、休闲旅客的出行方式选择模型。文献[2]运用随机效用理论与时间分配模型,研究了旅客出行时间价值与票价、旅客收入水平及旅行时间的关系。文献[3]通过研究高铁与航空运输的旅客选择行为,得到不同类型旅客的支付意愿。文献[4]通过研究票价对需求变化的影响,利用铁路与航空运输间的交叉价格弹性来改进铁路票价制定方法。文献[5]研究了基于旅客出行时间价值的票价制定方法。文献[6]分析旅客选择行为,表明出发时段是旅客选择的关键因素,并以此构建考虑出发时段偏好的旅客平行车次选择模型。文献[7]研究了基于作业成本法的铁路票价制定方法。文献[8]探讨了高铁基准票价制定方法。文献[9-11]研究了多种交通方式竞争条件下的铁路票价制定方法。文献[12]在旅客市场细分的基础上构建了高铁动态定价的稳健优化方法。文献[13]构建了基于旅客选择效用最大化的时间价值模型及差别定价模型。文献[14]研究了高铁单列车、多区段的动态定价及票额分配问题。文献[15]研究了高铁单列车、多列车的差异化动态定价问题。但既有旅客选择行为研究通常从宏观上将高铁列车作为一种运输方式,而未进行精细化划分,并且很少考虑同一OD间多列车之间的相互差异性[1-5]。在票价制定方面,既有文献主要研究了基于成本[7-8]、多种交通方式选择[9-11]、旅客市场细分[12]、旅客出行时间价值[13]的高铁列车定价问题及单列车在单区段和多区段的定价策略[14-15],而对于同一OD间多列车的差异化联合定价研究较少。
本文针对既有研究的不足,从更加精细化的角度出发,充分考虑同一OD间不同高铁列车在发车时段、运行时间上的差异性,并以此为分类依据研究旅客对同一OD间不同高铁客运产品的选择行为,在此基础上,以铁路部门为上层决策者,旅客为下层决策者,构建以铁路部门收益最大化,旅客广义出行费用最小化为目标的高铁客运产品的差异化定价双层规划模型,并设计基于灵敏度分析的启发式算法,最后通过实例验证模型的有效性。
1 问题分析
对同一OD间的高铁客运产品实施差别定价的关键是列车间具有差异性,并且旅客对这些差异性具有一定的选择偏好,因此在进行差别定价前需要分析旅客的选择行为。
1.1 旅客出行选择行为分析
高铁的同一OD间通常运行多趟列车,这些列车在发车时段、运行时间上具有差异性,旅客在选择时,通常会根据自身需求选择效用最大化的客运产品。本文根据同一OD间不同高铁列车在运行时间、发车时段、票价等方面的差异性,将高铁客运产品划分为j种类型,如表1所示。由于目前同一OD间同等席别的高铁客运产品票价相同,当将发车时段划分为k个时段,运行时间划分为m个水平时,则可以将同一OD间的不同高铁列车划分为不同类型的客运产品,即发车时段与运行时间的交叉组合。
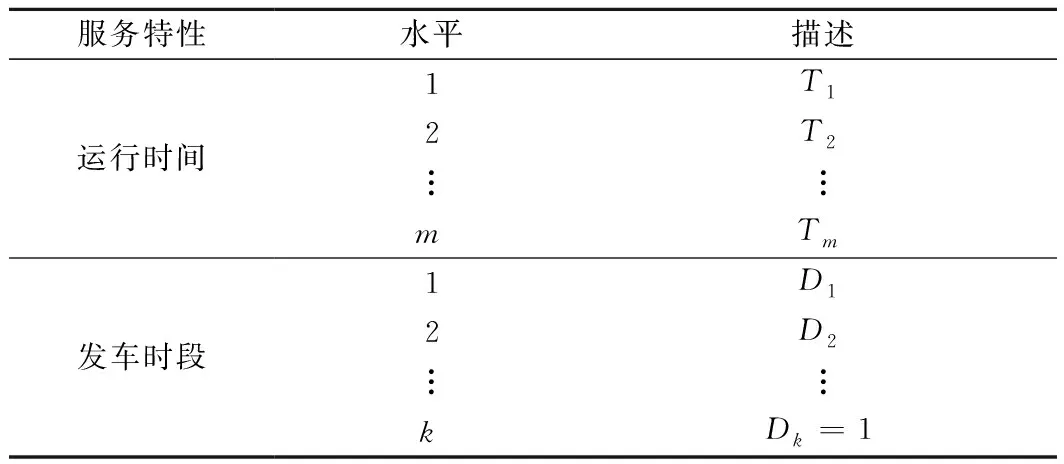
表1 高速铁路客运产品划分
在不考虑随机因素的影响下,旅客出行费用是出行效用的相反数,假设同一OD间有N种高铁客运产品,旅客选择第j(j=1,2,…,N,N=m×k)种产品的出行费用为Cj。本文选取票价、运行时间、发车时段为特性变量来描述旅客出行费用,即
Cj=ω1Pj+ω2Tj+ω3D1+ω4D2+…+ωk+2Dk
(1)
式中:Pj为第j种产品的票价,元;Tj为第j种产品的运行时间;Dk为第j种产品的发车时段,当列车发车时段水平为k时,仅Dk=1,其余均取0;ω1、ω2、ωk+2分别为票价、运行时间、发车时段的权重系数。
1.2 用户均衡配流分析
旅客在选择不同高铁客运产品出行时,根据效用最大化原则,通常会根据自身情况选择效用最大即广义出行费用最小的产品。当旅客选择某一高铁客运产品出行时,该产品的客流需求会相应增加,随之带来的是选择该产品的广义出行费用的上升,例如票价上涨等情况,使得部分旅客放弃选择该产品,而选择其他广义出行费用较低的客运产品,从而导致不同客运产品的广义出行费用发生新的变化,旅客根据不同客运产品广义出行费用的变化不断调整选择,最终使得各客运产品间的广义出行费用相等,小于或等于未被选择的客运产品的广义出行费用,客流在各客运产品间的分配更加均衡,即Wardrop原则。均衡配流模型为
(2)
(3)
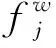
式 (3)表示各客运产品的客流量之和等于总的客流量。
2 高铁差别定价双层规划模型构建
高铁客运产品差别定价问题可以描述为以高铁票价制定部门为上层决策者,旅客为下层决策者的双层规划问题。
上层模型中以铁路部门在各OD各客运产品获得的客票收益最大化为目标,其目标函数为
(4)

OD对w间第j种产品票价的上下限约束为
(5)
考虑铁路运输的社会公益服务特性,票价不能高于一个票价上限,防止运输能力紧张时期票价过高,造成社会不良影响。同时不得低于一个票价下限,防止铁路票价过低造成收益损失。
下层模型从旅客出行的角度出发,目标函数为旅客的广义出行费用最小,从式(1)中可以看出影响旅客出行费用的主要因素是不同客运产品的票价,旅客会根据不同客运产品的票价做出相应的选择调整,最终使得不同客运产品间的客流量达到相对均衡稳定的状态,下层模型为
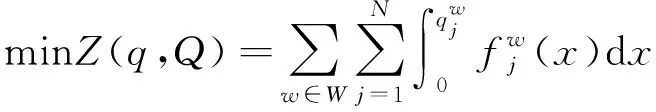
(6)
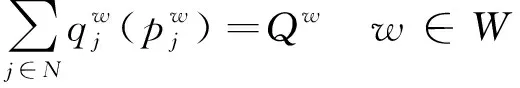
(7)
(8)
式(7)为同一OD对w间不同高速铁路客运产品的客流量之和。式(8)保证各客运产品的客流量非负。
不同OD间的需求函数可采用相同形式,但由于不同OD间起讫城市的发达水平不同,人们的出行需求也具有一定的差异性,因此对需求函数参数的影响程度也不同,需要对不同OD间的需求函数进行具体分析[16]。需求函数为
Qw=ABh(uw)
(9)
式中:A、B分别为OD对w起讫城市的相关系数;h(uw)为最小广义出行费用uw的函数,为单调递减函数。即当uw增加时,Qw必然下降;由于不同OD的起讫城市间运输能力及其人口规模的限制,需求总量应该是有界的。
而同一运输通道内的运输需求总量通常不是一成不变的,其会随着旅客广义出行费用的变化而发生改变,为了更加符合实际情况,在建模时应当考虑需求的弹性变化,构建弹性需求下的模型,因此对模型L1改进可得
(10)

(11)
(12)

综上通过在模型目标函数中引入需求函数的反函数,可以将模型转化为弹性需求问题。由于弹性需求问题直接求解的困难性,本文通过增加一条多余需求路段可以将弹性需求问题转换为等价的固定需求问题求解。
空余需求ew为实际需求与需求上限之间的差值,即
(13)

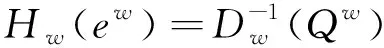
因此,式(10)中的第二项可以扩展为
(14)

(15)
由于Hw(ew)具有与普通阻抗函数相同的特征,可以将其视为运输通道内一种客运产品的广义费用函数,即在运输通道的每个OD间新增一个虚拟客运产品,该客运产品的客流量ew为函数的自变量。因此弹性需求问题通过增加一个虚拟客运产品可以转化为固定需求问题,即

(16)
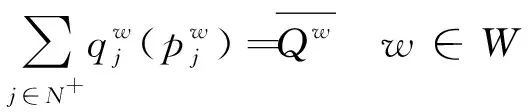
(17)
(18)
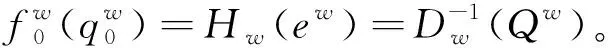
f(qj)=a(qj)b-Vj
(19)
式中:a、b为参数;Vj为第j种产品不考虑随机因素影响时的效用值,为式(1)的相反数。
则基于旅客选择行为的广义费用函数为
f(qj)=a(qj)b+ω1Pj+ω2×Tj+ω3D1+
ω4D2+…+ωk+2Dk
(20)
综上所述,模型L3为

ω1Pj+ω2×Tj]dx
(21)

(22)
(23)
3 启发式算法

利用灵敏度分析法可以求出变分不等式的解对扰动参数的导数,假定运行时间、出发时段等影响客流变化的因素不变,以票价作为扰动参数,则模型中各客运产品间的均衡配流模型可以用变分不等式为
fw(qw*)T(qw-qw*)≥0w∈W
(24)

(25)
(26)
(27)
若考虑票价p作为f(qw)中存在的扰动参数,即f(qw,p),则式(24)可以表示为
fw[qw*(p),p]T[qw-qw*(p)]≥0w∈W
(28)
fw(qw*(p),p)-φw=0w∈W
(29)
(30)
式中:φw为一个有N个相同元素的Lagrangian乘子向量。
假设y(p)=[qw(p),φw(p)]T,Jy(p)为式(29)和式(30)对于[qw(p),φw(p)]的Jacobian矩阵,Jp(p)表示式(29)和式(30)对于p的Jacobian矩阵,则有
(31)

(32)
将式(32)代入上层规划即可将上层规划模型转化为一般的非线性规划问题,进而可以采用现有方法求解。通过求解上层规划问题,又可以得到使目标函数最大化的各类客运产品的最优票价,将其作为新的票价代入下层模型中又可以得到新的均衡配流下的各客运产品的客流量,通过不断迭代即可实现对双层规划模型求解,得到收敛判断条件下的最优解,步骤如下:

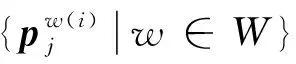
Step3确定反应函数。利用灵敏度分析法得到客运产品j的客流量对票价的导数,然后根据式(31)和(32)确定出反应函数的近似表达形式。
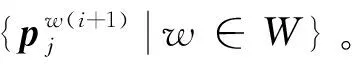


4 案例分析
4.1 基础数据
以北京—西安高铁为例进行分析,根据式(20)广义费用函数形式,确定发车时段、运行时间、票价的水平数来确定北京至西安高速铁路客运产品的数量。2017年4月东南沿海高铁实现浮动票价,允许票价最高上浮20%,本文以北京—西安高铁二等座为例,以20%作为浮动基数,其现有票价为515.5元,因此可以得到二等座票价的上、下限值分别为618.5、412.5元;将发车时段设置为4个等级,运行时间划分为3个水平,则可以将北京—西安的高铁列车划分为12种客运产品,见表2。

表2 北京—西安高速铁路客运产品属性
为得到式(20)广义费用函数中各个特性变量的系数,于2018年12月27日、28日,在北京西站候车大厅对乘坐北京—西安方向的旅客进行SP和RP调查,共计发放问卷450份,回收有效问卷429份,有效率达到95.3%。本文综合考虑旅客对列车票价及运行时间的个体异质性,用ML模型对旅客的出行选择行为进行描述,即式(20)中ω1,ω2为服从一定分布的随机变量。根据调查数据,利用Biogeme软件对ML模型进行参数标定,得到的广义费用函数的系数见表3,并且取a=0.65,b=0.4。

表3 广义费用参数表

f0(q0)=D-1(d)=0.1q0
4.2 差别定价方案
根据本文构建的模型和算法,利用Matlab对北京—西安的高铁列车进行差别定价,得到的各客运产品的票价和客流量及与现有固定票价制定模式的对比情况,见表4。

表4 北京至西安各高铁客运产品的最优票价及客流量
由表4可知,通过差别定价不同客运产品的票价及客流量较现有固定票价模式都有所变化,差别定价方案可以根据不同客运产品的特点调节票价来引导客流需求,从而提高客票收益。如客运产品2为旅客最偏好的选择,通过差别定价,其票价提升至566.5元,提高约9.89%,虽然客流量较固定票价的客流量下降约8.25%,但是票价的上涨使得获得的客票收益有所提高。差别定价与固定票价的对比情况见图1,两种方案的收益对比情况见表5。

图1 差别定价与固定票价对比情况

表5 两种方案收益对比情况
从图1和表5可以看出,差别定价通过调节票价使得各类客运产品的客流更加均衡,并且较现有固定定价方法,差别定价方法使得获得的客票收益增加527 738元,因此本文所构建的差别定价方法可以使高速铁路收益提升约6.1%,从而验证了本文所构建模型和算法的有效性。
5 结论
(1)本文通过对同一OD间列车在运行时间、发车时段上的差异性分析,在综合考虑旅客出行选择行为的基础上,以铁路部门为上层决策者,旅客为下层决策者,构建以铁路部门收益最大化,旅客广义出行费用最小化为目标的高速铁路差别定价双层规划模型,并根据模型特点设计了基于灵敏度分析的启发式算法,最后以北京至西安的高铁列车为例验证了模型的有效性。
(2)与现有的固定票价制定方式相比,利用本文模型得到的差别定价方案通过调节各客运产品的票价来引导客流需求在不同客运产品间的均衡分配,有效提高了各类产品的能力利用率,并且能够使铁路收益提高约6.1%。
(3)本文仅研究了同一OD间不同高铁列车客运产品的差别定价问题,并且仅考虑二等座的情况,未来将进一步研究多OD、多等级席位的高速铁路差别定价问题。
