顾及降雨及库水位因素的滑坡时滞分析与预测<br/>——以三峡库区新铺滑坡为例

顾及降雨及库水位因素的滑坡时滞分析与预测
——以三峡库区新铺滑坡为例

2021-05-13黄观文王家兴白正伟

地球科学与环境学报 2021年3期

黄观文，王家兴，杜源，白正伟，王铎

(长安大学地质工程与测绘学院，陕西西安 710054)

0 引言

中国每年地质灾害频发，滑坡在所有类型的地质灾害中占比近70%。三峡库区地质条件复杂，库岸裂隙发育，分布了多达2 619处涉水滑坡，其中700余处滑坡在库区蓄水运营后有复活迹象，是中国地质灾害的重灾区[1-2]。受季节性强降雨以及周期性库水位涨落等因素影响，库岸滑坡的失稳变形机制十分复杂。因此，分析此类滑坡变形特征，研究如何充分利用库水位、降雨、位移等监测数据对滑坡进行预测预报，对库岸滑坡防灾减灾具有切实意义。

现阶段，滑坡预测的研究热点主要是基于多源数据建立综合预测模型，即通过综合分析外界影响因子对滑坡的作用机制而建立的基于位移-诱因的预测模型[3-6]。滑坡变形是一个复杂、作用机理不明确的过程，具有明显的灰色系统特征。多变量灰色系统理论方法可以综合利用其顾及多影响因子以及灰色系统的特性，整体、全局、动态地分析预测滑坡位移[7-8]。潘国荣等改进了正规矩阵，将诱发因素作为非参数变量引入灰色模型，充分利用了多源数据[9]；Wu等在传统灰色模型中加入时间项，克服了灰色模型在计算背景值和时间响应函数的不足[10]。谢金华研究了灰色模型在短临预报中的适用性和局限性，认为GM(1,1)模型对加速变形近似指数性滑坡的适用性更强[11]。由此可见，灰色模型在滑坡预测中得到了广泛研究。

然而，很多研究指出库岸滑坡位移速率对降雨、库水位涨落等诱发因素的响应具有一定的滞后性[12-13]，即当期降雨及库水位涨落的影响并不会立刻在滑坡位移速率上显现出来，而是会在若干天后才显现出来，但是当前大多数对这一时滞特征的研究只停留在定性分析，而少有定量研究。基于此，本文结合三峡库区库水位涨落数据、奉节气象站降雨数据及新铺滑坡GNSS位移监测数据，定量分析滑坡对这两种诱发因素的滞后响应时间，并将这一时滞参数加入到多变量灰色模型中，即GM(1,N)模型，建立一种顾及库水位及降雨时滞因素的滑坡预测模型，对位移进行预测；通过与GM(1,1)模型及考虑时滞因素的GM(1,3)模型进行对比分析，验证将时滞因素引入滑坡位移预测模型的可行性。

1 时滞GM(1,N)模型的构建

为了得到滑坡位移速率对库水位和降雨量的滞后响应时间，本文首先对位移速率和诱发因素进行时滞互相关分析，确定时滞参数，进而代入到时滞灰色模型中进行预测，以提高预测精度。

1.1 时滞互相关分析

三峡库区库岸滑坡的位移速率对降雨、库水位涨落等诱发因素的响应具有一定的滞后性。一方面，库水位快速下降会导致滑坡体内地下水与外部库水位产生高差，即滑坡体内地下水位下降速度滞后于库水位下降速度，产生了一定的渗透压力，渗透压力指向坡体外部；另一方面，长时间降雨使得地表水渗入滑坡体中，增加了滑坡体的自重和下滑力，同时软化了滑带土，摩擦力减小，进而导致滑坡变形加速。在库水位下降和强降雨相互叠加的双重影响下，使得滑坡变形加剧[14-16]。这些诱发因素对滑坡产生影响需要一定的时间，如果不顾及这一时滞因素，必将使得预测结果偏离，因此，在利用多源诱发因子进行分析预测时，首先要对这些因素进行时滞分析。

随机序列的数字特征常用互相关函数进行表征，对时间序列进行互相关分析是研究两个序列之间时延关系的有效工具，这在声学测距等系统中被广泛应用[17]。对于两离散时间序列信号X1(k)和X2(k)，二者的互相关函数R(n)为

(1)

式中：k为时刻；N为总时间；n为延迟时间。

若X1(k)和X2(k)分别为滑坡位移速率序列和降雨量(库水位)序列，则当互相关函数R(n)取得最大值的延迟时间时，即为位移速率对降雨量(库水位)的响应滞后时间，这一时间记为τ。

1.2 时滞GM(1,N)模型

滑坡从缓慢蠕变到变形失稳的全过程中，受多种因素影响，一般包括地质地貌、地层岩性、降雨和库水位等诱发因素、人类活动等，但目前人类还无法准确描述每项因素的影响程度与作用机理，即滑坡的变形机理并不完全明确，多种影响因素并存也给定量分析滑坡形变带来了不确定因素。因此，滑坡具有明显的灰色系统特征。

GM(1,N)模型是灰色模型中表示输入输出系统的状态模型，反映了当前系统变量在当前时刻的取值和变化率受另外N-1个因子影响的特征，适用于受多因子影响的滑坡动态分析预测。然而在实际应用中，某个参数受多个因素影响，且响应滞后的情况十分普遍[18-19]，即系统在某时刻的输出和变化受系统前期输入的影响，在时滞互相关分析中已经求得了这一滞后时间。

假设滑坡位移速率时间序列为

(2)

式中：t为时间；角标(0)表示该序列未经累加操作。

其他时滞相关因子的时间序列为

i=2,3,…,N

(3)

式中：τi为该时滞相关因子的滞后时间。

(4)

(5)

对N个序列建立的GM(1,N)白化微分方程为

(6)

将以上微分方程离散化，可得到

(7)

式中：a、bi为微分方程的系数。

令

(8)

(9)

式中：B为累加矩阵；Y为常数项向量。

(10)

微分方程(7)的近似时间响应式为

(11)

(12)

由此，时滞GM(1,N)预测模型建立，整个数据处理流程如图1所示，主要包括时滞互相关分析和预测两部分。

图1 时滞灰色模型建模流程图Fig.1 Modeling Flow Chart of Time-delay Grey Model

2 算例分析

本文以三峡库区新铺滑坡作为研究对象，数据选取2019年12月16日至2020年11月5日新铺滑坡的GNSS位移监测数据、奉节气象站降雨数据以及三峡库区库水位涨落数据。

2.1 新铺滑坡概况

新铺滑坡地处三峡库区奉节县安坪镇新铺村，位于长江南岸，与三峡大坝直线距离为158 km。该滑坡为顺层—微切层特大型滑坡群，滑坡群平面形状似撮箕形，上窄下宽，滑坡前缘高程为81～85 m，后缘高程为810 m，为涉水滑坡。滑体平均厚度为22.7 m，总体积为3 410.89×104m3，属特大型滑坡。

2019年12月在新铺滑坡布设了10套实时低成本北斗/GNSS监测设备(图2)，该设备可以自动化获取滑坡体秒级的绝对位移序列[20-21]。早期要想获取滑坡体的绝对位移，常采用静态GNSS相对测量技术定期对滑坡进行观测，获取到的数据时间分辨率低，即每期数据间隔时间长，难以精确掌握滑坡的实时动态变化，因此不能对滑坡的变形特征进行严密分析；而利用GNSS-RTK技术可以得到更加丰富的数据，提供了分析滑坡位移速率对诱因滞后响应时间的可能。

图2 三峡库区新铺滑坡监测点位分布图Fig.2 Distribution Map of the Monitoring Points of Xinpu Landslide in Three Gorges Reservoir Area

2020年5月初，新铺滑坡开始出现加速滑动趋势，且位移速率逐渐增大，7月底位移速率达到峰值，10月之后随着三峡水库的蓄水，库水位也在不断抬升，同时降雨量开始减少，滑坡位移速率也逐渐减小(图3～5)。由此可以看出，库岸滑坡形变和降雨量及库水位高程关系密切。2020年入汛以来，中国南方遭受了严重的暴雨洪涝灾害，长江中下游出现较重汛情；国家气候中心数据显示，重庆2020年的降雨量打破1961年以来的历史纪录[22]。如何在削减下游洪峰、保障下游人民生命财产安全、加快库区调度效率的同时，保证上游滑坡稳定，就需要研究库水位涨落、降雨等对滑坡的作用机制。

图3 各监测点累计位移时间曲线Fig.3 Cumulative Displacement Time Curves of Each Monitoring Point

2.2 新铺滑坡的时滞分析与预测

首先分别对滑坡位移速率与降雨量、库水位高程进行时滞互相关分析，本文将滑坡位移速率对降雨及库水位的响应滞后过程进行简化，即假设滞后时间保持恒定。

2.2.1 时滞互相关分析

降雨从地表向地下渗入是一个较为缓慢的过程，在这一过程中，降雨量序列的波动特性也得到了平滑。因此，在进行时滞互相关分析前，对原始降雨量序列利用移动平均法进行平滑处理。同时，由于使用移动平均法后会使序列产生滞后，故将移动平均处理后的序列与原始序列进行对齐操作，以确保结果的准确性。

对滑坡位移速率、降雨量两个序列进行互相关函数计算，结果如图6所示。从图6可以看出，除XP02、XP05、XP10等3个监测点以外，位移速率对降雨量的响应滞后时间稳定分布在4～6 d，平均滞后时间为5 d，相关系数大于0.5，成显著相关关系[23]。而XP02点、XP10点的位移与降雨量的相关系数极大值相比其他点位偏小，滞后时间在互相关序列上体现得也不稳定，考虑XP02点、XP10点最靠近长江，受库水位涨落的影响较大，降雨与库水位叠加影响使其与降雨量相关性降低。另外，由于XP05点靠近新铺滑坡的后缘，拉裂变形影响因素更多，故呈现出与其他点位差异较大的情况。因此，综合新铺滑坡整体情况，滑坡位移速率对降雨量响应滞后时间(τ1)取值为5 d。

图5 日降雨量与库水位高程时间序列Fig.5 Time Series of Daily Precipitation and Reservoir Water Level Elevation

图6 位移速率-降雨量时滞互相关序列Fig.6 Time-delay Cross Correlation Series Between Displacement Rate and Precipitation

对滑坡位移速率、库水位高程两个序列进行互相关函数计算，结果如图7所示。从图7可以发现，位移速率与库水位高程成负强相关关系，其中XP04点的相关性更是高达-0.91。除XP05点以外，其他点位对库水位涨落响应的滞后时间为29～33 d，平均滞后时间为31 d，其中XP09点的滞后时间最短，为29 d，XP06点、XP07点滞后时间稍长，分别为33、32 d。考虑XP09点更靠近长江，容易受到库水位涨落的影响，而这一影响传导到滑坡中后部的XP06点、XP07点需要一定的时间，故后缘滞后时间稍长。同时，库水位涨落直接影响滑坡体地下水位的变化，进而影响滑坡的深部位移，而GNSS监测的是地表位移，这一深部位移传导到地表也需要一定的时间，故位移速率滞后时间比地下水位对库水位的滞后时间更长。而降雨直接影响地表位移，故滞后时间较短。除此之外，由于所用库水位数据为三峡库区数据，而新铺滑坡距离三峡大坝158 km，三峡大坝的蓄洪、泄洪操作传递到上游还需一定的时间，也一定程度使得计算的滞后时间延长。综上所述，综合新铺滑坡整体情况，滑坡位移速率对三峡水库库水位涨落响应滞后时间(τ2)取值为31 d。

图7 位移速率-库水位高程时滞互相关序列Fig.7 Time-delay Cross Correlation Series Between Displacement Rate and Reservoir Water Level Elevation

综上所述，可根据每个监测点对降雨量响应滞后时间τ1和库水位涨落响应滞后时间τ2，建立时滞GM(1,3)模型。

2.2.2 时滞GM(1,3)模型预测算例

以变形量最大的XP04点为例，对库水位高程及降雨量波动较大的2020年6月20日到7月20日进行拟合建模，预测7月21日到8月5日共16 d的数据，样本数据如表1所示。基于XP04点的时滞互相关分析结果，取降雨量响应滞后时间τ1=5和库水位涨落响应滞后时间τ2=31，代入时滞GM(1,N)模型中，对微分方程系数进行解算，求解近似解并做还原计算得到预测值，建立位移速率对降雨及库水位的时滞GM(1,3)模型。

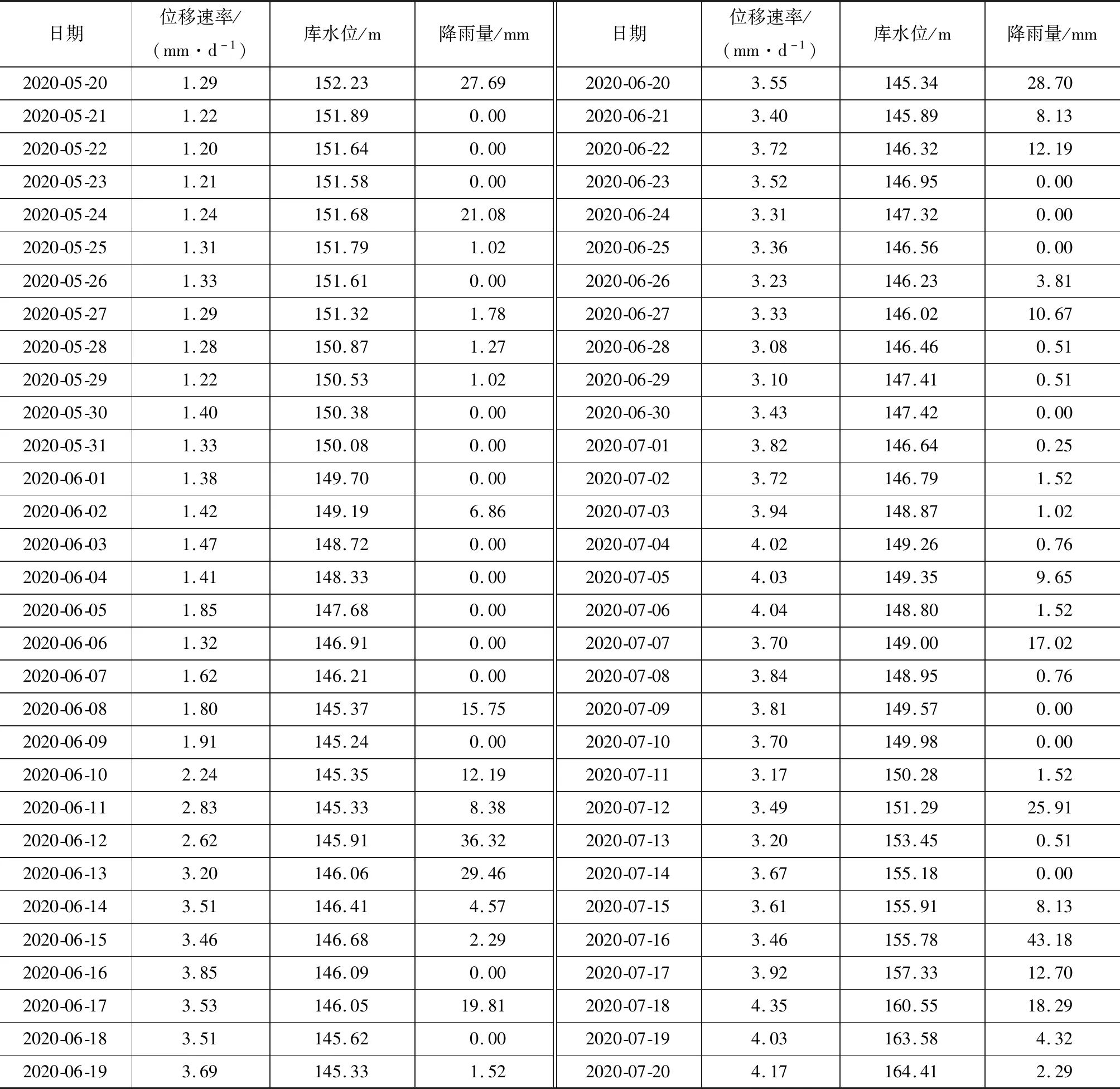
表1 XP04点位移速率及库水位高程、降雨量样本数据Tab.1 Sample Data of Displacement Rate,Reservoir Water Level Elevation and Precipitation of Monitoring Point XP04

在对2020年6月20日至7月20日的位移速率进行拟合建模时，由于加入时滞参数，实际上使用的是2020年5月20日至6月20日的库水位数据和6月15日至7月15日的降雨数据，所以在预测过程中可以充分利用已采集到的2020年6月21日至7月6日的库水位数据和7月15日至7月20日的降雨数据。在实际预测过程中，采用滑动窗口式的滚动预测模式，流程如下：读入数据时设置滑动窗口的大小为31 d，每预测一个值，将此值加入原来的数据集，并舍去一个最老的数据；同时，利用已知的2020年6月20日至7月20日的库水位和降雨数据对下一个值进行预报。由于要预报16 d，而已知的先验降雨数据只有5 d，所以对第6天到第16天的数据采用位移速率对库水位高程的时滞GM(1,2)模型进行预测。如此循环，直至完成预测目标。

为了分析和比较引入时滞参数前、后模型对位移速率预测的效果，时滞GM(1,3)模型与GM(1,1)模型和未顾及时滞因素的GM(1,3)模型对同一时间预测的位移速率进行对比验证，计算结果如图8所示。

图8 3种模型下预测值与实测值对比Fig.8 Comparison Between Predicted Value and Measured Value Under Three Models

2.2.3 模型精度评估

为全面分析时滞GM(1,3)模型对滑坡位移速率的预测性能，基于相同数据，通过与GM(1,1)模型和未顾及时滞因素的GM(1,3)模型进行对比，选用均方根误差(RMSE,RE)、平均绝对误差百分比(MAPE,ME)以及拟合优度(R2)对预测结果进行评价,分别评价模型实测值与预测值的精度水平、平均偏差及模型拟合优度。

(13)

(14)

(15)

由表2可知，时滞GM(1,3)模型的拟合优度达到0.702，相比GM(1,1)模型和未顾及时滞因素的GM(1,3)模型，均方根误差分别提升了53.8%和58.3%，平均绝对误差百分比分别降低了7.19%和7.47%。在各项指标上,时滞GM(1,3)模型都显著优于传统GM(1,1)模型、GM(1,3)模型，其中由于传统GM(1,3)模型未顾及时滞因素，其精度甚至低于传统GM(1,1)模型，也说明了考虑时滞因素对滑坡预测的重要性。

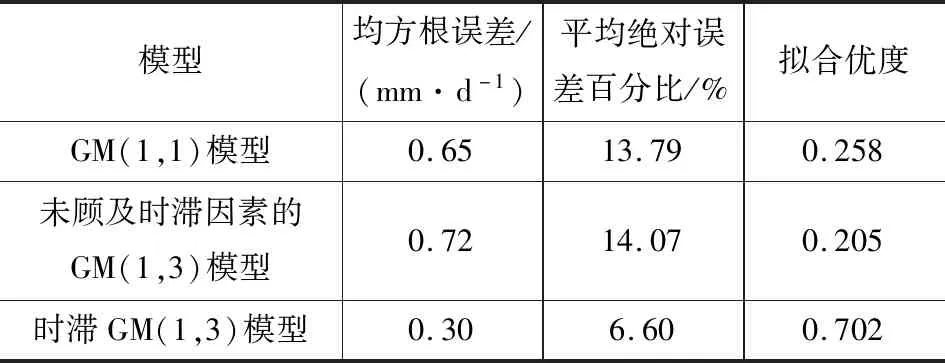
表2 预测效果评价参数Tab.2 Prediction Performance of Algorithms

综上可知，顾及降雨与库水位的时滞GM(1,3)模型考虑了滑坡位移速率对降雨量与库水位高程响应的滞后性，并且加入这一因素后预测精度提升明显，在滑坡位移速率预测领域具有一定的工程应用价值。

3 结语

(1)三峡库区新铺滑坡位移速率与降雨量显著相关，对降雨量的响应滞后时间约为5 d，滑体中后部受降雨影响更明显；位移速率与库水位高程高度相关，对三峡库区库水位涨落的响应滞后时间约为31 d，滑坡前缘受库水位涨落影响更明显，且离长江越近，滞后时间越短。

(2)位移速率是反映滑坡运动状态的重要参数；运用时滞灰色模型对滑坡位移速率进行短期预测是切实可行的。将时滞参数引入模型可明显提高时滞GM(1,3)模型预测精度及可靠性，其拟合优度达到0.702，相比GM(1,1)模型和未顾及时滞因素的GM(1,3)模型，预测精度分别提升了53.8%和58.3%，平均绝对误差百分比分别降低了7.19%和7.47%。顾及降雨与库水位的时滞GM(1,3)模型对于提前了解滑坡运动状态，提升三峡水库调度效率可起到一定的积极作用，在指导库区日降水幅度及库岸滑坡防灾减灾领域具有一定的工程应用价值。

(3)随着滑坡监测技术的快速发展，对滑坡各类诱发因素的监测手段不断完善，监测数据的实时性和采样率也得到提升。本文提出的顾及多变量时滞因素的GM(1,N)模型可利用更丰富的数据对滑坡进一步分析提升精度，进而得到相对普适性的规律，并为滑坡形变物理机制的研究提供支撑。

谨以此文庆祝长安大学七十周年华诞！七十载风雨兼程，遍撒硕果，造就英才无数；七十载励精图治，厚德载物，喜赢美誉天下！

《长安大学，我想对您说》

我们，以祖国花朵模样

轻轻地依次来到您身旁

天真幼稚地享受着您的爱和表扬

忽视着您的付出和培养

受伤了，您轻轻张开庇护的翅膀

讲述着天道酬勤的主张

犯错了，您谆谆教诲如海的胸膛

传授着对待挫折的良方

打击了，您永远支撑我们的坚强