给核心概念以核心地位
2021-05-12孙佳威
【摘 要】核心概念是学生认识事物本质的源头,是逻辑推理的依据,是理解数学知识、解决问题的支柱。教学中给核心概念以核心地位,为探寻数学本质、撬动学生思维提供了更多的可能。本文以核心概念“计数单位”为例,谈它在运算学习中所起的“牵一发而动全身”的作用,以此说明核心概念在数学学习中的核心地位。
【关键词】数学学习 核心概念 核心地位
孙佳威
任职于北京市朝阳区星河实验小学,北京市数学特级教师、高级教师。获中国教育学会小学数学教学专业委员会先进工作者、课程教材研究所优秀教研员等称号。从教30余年,一直致力于学习和推广马芯兰数学教育思想,形成了“凸显核心概念、实现数学理解”的课堂教学特色。被聘为北京教育科学研究院儿童数学研究所兼职研究员,教育部“国培计划”—示范性教师工作坊高端研修项目小学数学工作坊主持人,教育部小学数学学科教研基地核心组成员,大连大学初等师范学院客座教授等。主持研发“小学数学能力目标体系”等15项课程,著有《开启学生的数学思维:对马芯兰数学教育思想的再认识》,担任“儿童数学教育丛书”《在涂画中学数学》副主编,教育部《小学数学教学装备配置标准(JY/T 0617—2019)》编写组核心成员。发表文章30余篇,多篇论文获中国教育学会小学数学教学专业委员会、北京市教育学会数学论文评比一等奖。
数学概念反映了现实世界空间形式和数量关系的本质属性,是数学知识的基本细胞。没有数学概念就无法构成数学的知识体系。在诸多数学概念中,有一类属于最基本的概念(或原始概念),这些概念在反映事物的内在联系方面,较其他概念而言,更接近本质,更具有概括性。因此,我们称之为数学中的“核心概念”。
我国著名的数学教育家马芯兰老师就核心概念(核心知识点)的“核心”做过进一步解读,她认为,既为“核心”就说明它不是只与某个下位知识单线联系,而是与众多的相关知识都有密切联系。数学知识自身具有结构性,这种结构性体现在它是立体的、耗散式的,而核心概念就处于这个耗散结构的节点上,它是学习的源头活水。马芯兰老师对核心概念的精辟解读,直戳数学知识、数学教学的本质。这也要求我们在教学时,分析数学概念间存在的逻辑联系和迁移条件,加强最基本概念(即核心概念)的教学。只有最基本的概念掌握好了,学生才具备自主进行下一步学习的关键性条件,也才会处理好与其他相关知识的关系。
“给核心概念以核心地位”,以核心概念为基点,让学生联想,使他们自主地(或者在点拨下)发现更多的联系,这样,原有的平衡就会不断被打破,广泛的迁移学习才能不断产生。在数学知识的探索中引发学生的数学思维,帮助学生运用数学思维、发展数学思维,进而使具体的数学内容学习摆脱单一的、零散的、碎片化的状态,使学生掌握整体的、网状的、相互关联的知识体系和思维方法,从而实现思维的深刻性、内容的拓展性和方法的可迁移性,这既需要教师对知识结构有清醒且比较深刻的理解,也需要教师对核心概念有明确的认识。
下面,我们就以核心概念“计数单位”为例,谈一谈它在运算学习中的核心地位,以此说明核心概念在数学学习中的核心地位。
一、核心概念“计数单位”在加减法运算中的体现
1. 整数加减法运算
例如,9+3,如果从数数的角度计算结果,其实就是数计数单位的个数。从9开始,以“1”为单位,连续累加3次,就得到12这个结果,这个运算的过程就是计数单位个数累加的过程。同样,运算“9+3”,从9开始,以“1”为单位,先累加1次到10,也就是先凑成10,再累加2次得到12。“满十进一”,由此,产生新的计数单位“十”。这样看,可以1个1个地数,也可以10个10个地数,还可以100个100个地数……在计数单位个数不断累加的过程中,就会产生“一”“十”“百”,甚至更大的新的计数单位。计数单位个数不断累加,方便和满足了数量级扩展后大数加减法的计算。
减法与加法互为逆运算的关系,所以减法的实质是计数单位个数递减的运作过程。例如,36-8(如图1所示),个位的6减8不够减,就要从3个十中借走1个十,拆开变成10个一,以“一”为单位,从中递减8次,剩余2个一,再把这2个一和原来的6个一累加起来,得到8个一;3个十因为借走1个十,所以还剩下2个十;最后36-8等于28。
整数加减法计算以核心概念“计数单位”为核心,通过计数单位个数的累加和递减的运作过程,帮助学生理解数的内部结构,进而理解运算的意义。
2.小数加减法运算
小数的计数系统是从整数的十进制系统延伸而来,小数运算的核心与整数相同,也是计数单位个数累加和递减的运作过程(如图2、图3所示)。
1.23+3.45=4.68
2.47-1.25=1.22
3. 分数加减法运算
分数加减法同整数、小数加减法的意义是一样的,这也就决定了分数加减法的运算实质同样是计数单位个数的累加和递减。例如,异分母分数加减法(如图4所示),由于它们的计数单位(分数单位)取决于它们各自的分母,所以,在进行加减法运算时,首先需要找到一个对二者来说都能获取计数值的新的计数单位(分数单位)。通过通分,我们找到这个新的计数单位(分数单位),累加或递减,就得到了两个异分母分数的和或差了。
这样,整数、小数、分数加减法运算,就以核心概念“计数单位”为核心紧紧地勾连在一起了。
二、核心概念“计数单位”在乘除法运算中的体现
1. 整数乘除法
例如,12×3(如图5所示),图中表示的是3个12是多少。其中“12”是标准,由1个十和2个一组成,“3”是有3个这样的标准。以“十”为计数单位累加3次,以“一”为计数单位2个2个地累加3次,最后把各自的得数再累加,得到结果36。除法也一样,42÷2(如图6所示),把42平均分成2份,求一份是多少。先以“十”为单位递减,把4个十平均分成2份,每份得到2个十;再以“一”为单位递减,把2个一平均分成2份,每份得到1个一;最后把2个十和1個一累加,得到结果21。
整数乘除法,说到底还是以核心概念“计数单位”为核心,是计数单位的累加和递减的运作过程。
2. 小数乘除法
小数乘法运算包括小数乘整数和小数乘小数。例如,0.2×3(如图7所示),表示的是3个0.2是多少,其中“0.2”是标准(图7中2个小条),标准是由2个0.1组成的,“3”是有3个这样的标准。以“0.1”为计数单位,2个2个地累加3次,得到结果0.6。再如,0.2×0.3(如图8所示),显然用0.1作计数单位去计算已经行不通,这时就需要寻找一个新的计数单位,而这个计数单位是相对隐性的。我们把“1”平均分成10份,取其中2份,是0.2。0.2×0.3表示的是0.2的是多少,即把0.2再平均分成10份,取其中的3份。這时,新的计数单位0.01就产生了。以“0.01”为计数单位累加6次,得到结果0.06。用算式表示为 0.2×0.3=(0.1×0.1)×(2×3)=0.06。 由此可见,小数乘法的运算核心说到底还是小数计数单位个数累加的运作过程。
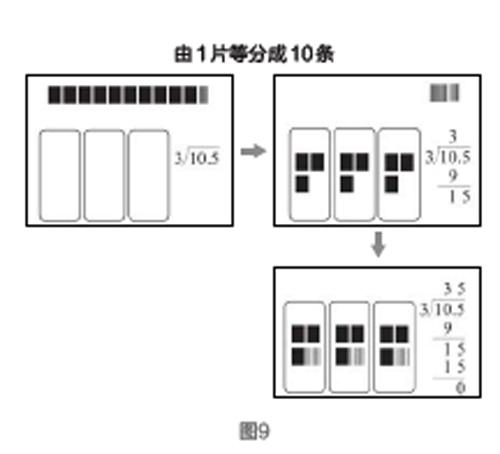
我们再看小数除法运算,例如,10.5÷3(如图9所示),先把10个一平均分成3份,每份分到3个一(9÷3=3),剩下1个一和5个0.1没法直接平均分成3份,所以把“一”转化成“0.1”之后再分,“一”里面有10个0.1,10个0.1加上5个0.1等于15个0.1,用15个0.1除以3,等于5个0.1,最后把分别得到的3和0.5累加,得到运算结果3.5。
小数除法,其本质与小数乘法一样,只不过是计数单位个数递减的运作过程。当高一级的计数单位不够平均分时,需转化为低一级的计数单位继续分,最终获得运算结果。
3. 分数乘除法
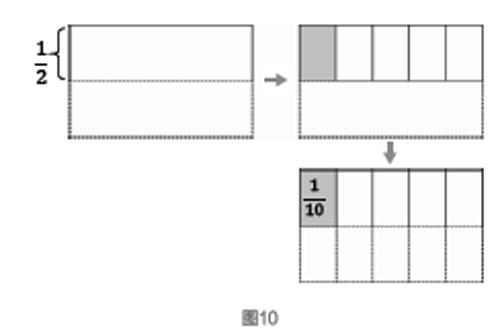
分数乘法包括分数乘整数和分数乘分数,是计数单位(分数单位)个数累加的运作过程。其运算意义与小数乘法运算意义相同,这也说明了两者运算实质是相同的。例如,×(如图10所示),表示的是
的是多少,需要把平均分成5份,取其中的1份,这显然需要新的计数单位(分数单位)。我们把“1”平均分成(2×5)份,找到了新的计算单位(分数单位),再进行累加就可以得到最终的结果。?
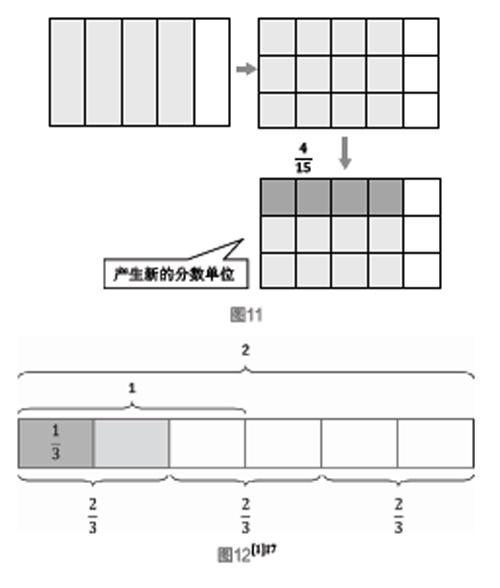
分数除法包括分数除以整数、整数除以分数和分数除以分数。相对于其他的运算而言,分数除法比较难理解。例如,分数除以整数,÷3(如图11所示),4个平均分成3份,分数单位的个数不能正好平均分,这时候就需要产生新的计数单位,把大的计数单位细分成小的计数单位,分数单位的个数4变成了12,正好能够平均分。再如,整数除以分数,2÷(如图12所示),表示的是2里面有几个,2是以“一”为计数单位的,的计数单位(分数单位)是,计数单位不同,这时候就要把大的计数单位细分成小的计数单位,2就细分成了,这时再做÷,计数单位(分数单位)的个数就可以相除了,结果是3。由此,分数除法的运算核心也是计数单位(分数单位)个数递减的运作过程。当高一级的计数单位不够平均分时,需要转化为低一级的计数单位继续平均分,最终获得运算结果。
从上面的分析中,我们可以清晰地看出核心概念“计数单位”在运算学习中所起的“牵一发而动全身”的作用。它将零散的知识不断地吸纳进来,并连缀在一起,形成一个相互关联的知识结构[2]。从这里,我们也可以看出这个知识结构是动态生成的,因为它在不断地勾连新旧知识。这种不断勾连的过程,会使学生在研究其他数学知识时,从核心概念出发去研究,为他们理解数学逻辑之美奠定了坚实的基础。
马芯兰老师经常教导我们:学生一旦感悟了“核心概念”在学习中的核心地位,就具有了自主学习迁移的能力,因为他知道了知识的“根”在哪里。发现了知识的“根”,已学习的旧知识就具有了“生命”,自主迁移学习到的新知识也就必然成为思维创新的产物!
参考文献
[1] 董文彬.基于度量角度整体把握数的运算教学[J].新课程研究,2019(18):14-17.
[2] 马芯兰,孙佳威.开启学生的数学思维:对马芯兰数学教育思想的再认识[M].北京:北京师范大学出版社,2020:10-17.
责任编辑:赵继莹
724132105@qq.com
