考虑储能动态运行特性的充电站光储容量优化配置模型

2021-05-12桂强史一炜周云冯冬涵

电力建设 2021年5期

桂强, 史一炜，周云, 冯冬涵

(电力传输与功率变换控制教育部重点实验室(上海交通大学)，上海市 200240)

0 引言

随着新能源汽车规模的快速增长，充电负荷对电网的冲击愈来愈严重[1]。为缓解电网压力，《新能源汽车产业发展规划(2021—2035年)》提出[2]：推动新能源汽车与能源融合发展，促进新能源汽车与可再生能源高效协同，鼓励“光储充放”(分布式光伏储能系统充放电)多功能综合一体站建设。

目前，很多学者做了大量关于光储容量配置的研究。文献[3]考虑光储电站的售电收益、储能损耗成本以及光伏考核成本费用，优化光储电站的储能容量配置，但未优化光伏装机容量。以快充站收益最大化为目标，文献[4]利用退役动力电池作为储能系统确定最优充电站储能配置容量及额定功率，但是储能系统的出力被固定为额定功率，仅优化了储能系统的充放电状态，未计及储能系统出力灵活性的特点。有学者考虑用户侧基本电费，通过配置储能系统减小用户用电成本，并建立双层优化模型求解，但优化目标中忽略了储能系统的损耗成本[5]。当前关于储能配置的研究中，储能寿命损耗很少计入目标函数[6-7]。

关于储能寿命损耗成本的计算，国内外也已有一定的研究成果。通过改进雨流计数法[8]，文献[9]提出一种实时储能系统寿命损耗以及健康状态实时评估方法，计算时间小于15 ms，但是该方法仍然属于后验算法，无法纳入优化模型之中。根据储能系统循环次数与充放电深度(depth of discharge, DOD)关系曲线，文献[10]通过将20%～80%的DOD的循环次数取平均，确定固定的电池总吞吐量，以度电成本来量化储能损耗成本。文献[11]将不同DOD的吞吐量等效到额定DOD下的吞吐量来统计储能系统寿命损耗成本。

现有研究中，基于雨流计数法的寿命损耗模型难以嵌入优化模型，造成以度电成本计算储能系统成本误差较大，并且考虑储能系统寿命损耗时，容量衰减情况被忽略以致储能模型不够准确。同时，储能系统的运行过程中，其运行效率也不是静态的。文献[12]根据储能电池(battery energy storage, BES)的电流与效率曲线，建立储能系统效率模型，但是该文献直接利用效率与电流关系，未能阐述如何定义效率。文献[13]通过分段线性化处理储能效率与功率关系曲线，但是该文献也是仅直接提供效率与功率曲线，而电池厂商一般不会提供该曲线。当前研究的储能模型未能综合考虑储能系统寿命损耗、容量衰减以及动态效率特性。

基于上述研究的不足，本文首先根据储能容量衰减特性，建立储能系统动态健康状态(state of health, SOH)模型；考虑储能系统寿命损耗特性，建立储能系统动态寿命损耗模型；考虑储能系统运行效率特性，建立储能系统动态效率模型，最后，综合上述模型建立精细化的储能系统动态模型。并基于该模型，建立光储充电站最优光储配置混合整数非线性规划(mixed integer non-linear programming, MINLP)模型。由于没有成熟的算法求解MINLP，通过将此问题转化为双层规划模型，利用遗传算法求解。算例分析中，以上海市某光储充电站为例，验证该模型以及求解算法的有效性，并分析典型场景下光储充电站的优化运行策略。

1 精细化储能模型

1.1 容量衰减模型

随着储能电池充放电次数的累积，储能电池内部不断发生老化过程，电池内阻随之增长，容量不断衰减。如式(1)所示，一般认为，当储能电池的可用容量衰减至额定容量的80%或者内阻增长为初始内阻2倍的时候，储能电池将退役或会投入梯次利用[14]。

(1)

式中：Send为储能电池退役时的可用容量；Srated为储能电池的额定容量；Rend为储能电池退役时的内阻；Rini为储能电池初始内阻。

根据容量衰减和内阻增长情况，本文提出2种储能电池的SOH模型：

(2)

式中：SOHC表示以可用容量为参考的储能电池健康状态；Spresent为储能电池当前的可用容量；SOHR表示以内阻作为参考的储能电池健康状态；Rpresent为储能电池当前内阻。当SOHC为80%或SOHR为0%时，储能电池寿命终止。本文使用SOHC作为储能电池SOH评估标准。

储能容量衰减速率与充放电循环次数、DOD、温度以及充放电倍率紧密相关。储能电池的运行温度一般认为是可控的[15]，储能功率在设置出力范围内对寿命的影响可认为是静态的[16]，因而本文忽略温度以及充放电功率对寿命损耗的影响。

根据文献[17]的实验数据，通过归一化处理，得到实验曲线如图1所示，并且用式(3)能很好地拟合该曲线。

图1 储能SOH与寿命损耗关系曲线

SOH=g(Ltotal, loss)=a1e-a2Ltotal, loss+a3e-a4Ltotal, loss

(3)

dSOH=g′(Ltotal,loss)dLtotal,loss

(4)

SOH(t)-SOH(t-1)=g′(Ltotal,loss)Lloss(t)

(5)

式中：SOH表示储能电池当前可用最大容量；a1,a2,a3,a4为拟合系数；g(Ltotal,loss)为拟合函数；Ltotal,loss表示储能电池寿命损耗程度，Ltotal,loss=0表示储能电池处于全新状态，Ltotal,loss=1表示储能电池寿命已终结。式(4)为式(3)的微分式；式(5)为式(4)的离散化处理等效式，其中Lloss(t)为第t时段的寿命损耗，即储能电池SOH的时序变化式。

为简化模型，将g(Ltotal,loss)分段线性化处理，则g′(Ltotal,loss)为各分段的斜率(具体见附录A1节)。

1.2 寿命损耗模型

基于BES充放电循环次数与DOD实验曲线，建立BES寿命损耗模型[18]，如式(6)—(14)所示。

Lloss(t)=|F[SOC(t)]-F[SOC(t-1)]|

(6)

(7)

(8)

(9)

(10)

(11)

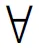
(12)

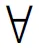
(13)

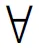
(14)

经过PWL处理，式(6)可写为式(15)：

(15)

式中：vch(t)/vdis(t)为标志储能充电/放电状态的0-1变量，当vch(t)/vdis(t)为1，表示储能在t时段处于充电/放电状态，反之则为0。

1.3 动态效率模型

因为储能电池内阻的存在，储能充放电效率不是静态的，而是随着充放电功率动态变化的。本文基于储能电池的充放电倍率与充放电时间关系的实验，提出储能电池的动态效率模型。

图2为某铅酸电池的放电时间与放电电流关系曲线[21]，一般用式(16)Peukert方程拟合放电时间随着放电电流的变化关系[22]，其中T为放电时间，I为放电电流，Cpeu与μ为拟合系数。放电电压U近似认为是线性的[15]，因此可以忽略电压变化的影响(证明见附录A2节)。同时，由于不同电流的放电电压变化较小，并且放电的起始电压与终止电压固定，因而本文认为电流与功率一一对应。在式(16)两端同乘UI，得到式(17)，其中Pdis为放电功率，Sout为放电过程释放的能量，Speu为固定系数。

图2 放电时间与放电电流关系

放电时间与充放电电流关系：

(16)

(17)

本文提出一种储能电池效率的计算方法：

(18)

(19)

为了简化模型，将放电功率分段线性化处理，如式(20)—(25)所示，对应的分段线性化效率为式(26)。

(20)

(21)

(22)

(23)

(24)

(25)

(26)

2 光储配置模型

2.1 目标函数

光储充电站光储容量优化配置的目标函数为储能电池全寿命周期内年均成本最小：

(27)

式中：Cgrid为充电站从电网的购电成本；CWLC为储能电池的全寿命周期成本(whole lifecycle cost, WLC)；Cpile为充电桩购置成本；CPV为光伏的配置成本；CEV为电动汽车提供的充电收益；Cdel为延迟电网升级的收益；N为储能电池的可使用年限。

2.1.1电网购电成本

电网购电成本由式(28)确定：

(28)

式中：ρs为场景s的概率；etou(t)为电网的分时电价；Ps,grid(t)为场景s在t时刻的购电功率。

2.1.2储能全寿命周期成本

CWLC主要包括：储能电池本体的购置成本Cbat、储能系统的功率成本Cbos、储能的运维成本CO&M以及储能残值回收价值Crec。

CWLC=Cbat+Cbos+CO&M-Crec

(29)

Cbat=ksSrated

(30)

Cbos=kpPrated

(31)

CO&M=kO&MPrated

(32)

Crec=krecCbat

(33)

(34)

式中：Prated为储能电池额定功率；ks为单位容量成本；kp为单位功率成本；kO&M为单位功率的运维成本；krec为储能电池残值回收系数;SOHrec为储能电池投入梯次利用时的SOH值;SOHter为储能电池寿命终止时的SOH值；Enew为储能电池在投入梯次利用前的总能量吞吐量；Erecycle为储能电池投入梯次利用到寿命终止阶段的总能量吞吐量。式(34)根据回收时储能电池的剩余吞吐量占电池全生命周期总吞吐量的百分比确定回收系数。

2.1.3光伏配置成本

光储配置成本与光伏装机容量有关[13]：

CPV=kPVSPV

(35)

式中：kPV为光伏发电系统的单位容量成本；SPV为光伏配置容量。

2.1.4充电收益

充电站为电动汽车提供充电服务收益：

(36)

式中：esell(t)为电动汽车充电价格，包含电价以及充电服务费；Ps,load(t)为充电站在场景s下第t时段的充电负荷。

2.1.5电网延缓升级价值

光储充电站配置储能能够帮助电网减小峰荷，缓解输电线路以及变压器压力，延缓配网升级改造。延缓配网升级价值为：

Cdel=kexpSdelay(1-1/eθN′)

(37)

式中：kexp为配网升级改造单位容量成本；Sdelay为延缓升级改造容量；θ为年利率；N′为延缓升级年限。

2.2 约束条件

模型约束除了第1节提到精细化储能电池的约束(式(5),(7)—(15),(20)——(26))之外，还有如下约束：

0≤N≤Nmax

(38)

(39)

Prated≤Srated

(40)

Ps,grid(t)+Ps,dis(t)+Ps,pv(t)=Ps,load(t)+Ps,ch(t)

(41)

0≤Ps,ch(t)≤vs,ch(t)Prated

(42)

0≤Ps,dis(t)≤vs,dis(t)Prated

(43)

vs,dis(t)+vs,ch(t)≤1

(44)

(45)

SOCs(t)-SOCs(t-1)=

(46)

(47)

同时，为了降低约束的复杂度，将绝对值约束式(15)松弛为约束式(48)和(49)。由于式(47)储能电池寿命损耗的限制，Ls,loss(t)会主动取其下限值，即|f(SOCs(t+1),Λ)-f(SOCs(t),Λ)|。

Ls,loss(t)≥f[SOCs(t+1),Λ]-f[SOCs(t),Λ]

(48)

Ls,loss(t)≥f[SOCs(t),Λ]-f[SOCs(t+1),Λ]

(49)

3 基于遗传算法的双层求解算法

显然，该光储充电站光储优化配置模型为MINLP模型，没有成熟的算法求解，本文提出双层优化[23]求解思路,如式(50)所示。首先提取出部分变量作为外层变量，并将其作为参数传入内层，外层通过全局寻优的遗传算法(genetic algorithm，GA)求解，内层为混合整数线性模型，利用成熟的商业求解软件求解。

(50)

Prated、Srated、SPV以及N作为外层变量，并作为参数传递给内层求解。由于SOH(t)的存在，内层可通过等效处理，转为MILP模型求解(等效说明见附录A3节)。约束式(10)、(45)、(46)分别转化为式(51)—(53)。

(51)

(52)

SOCs(t)-SOCs(t-1)=

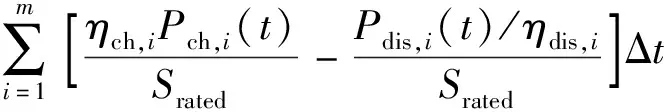
(53)

具体求解流程如图3所示。

图3 基于GA的双层模型求解流程

4 算例分析

4.1 参数设置

本文以上海市某光储充电站为例，验证提出的光储充电站光储优化配置模型以及基于GA的双层求解算法。电动汽车充电站购电电价参考上海市一般工商业的分时电价[24]。充电站选取磷酸铁锂电池作为储能电池，电池数据参数参考文献[25]，具体参数如表1所示，储能电池的SOH分段参数如表2和图4所示。储能寿命循环次数与SOC函数关系如式(54)所示：

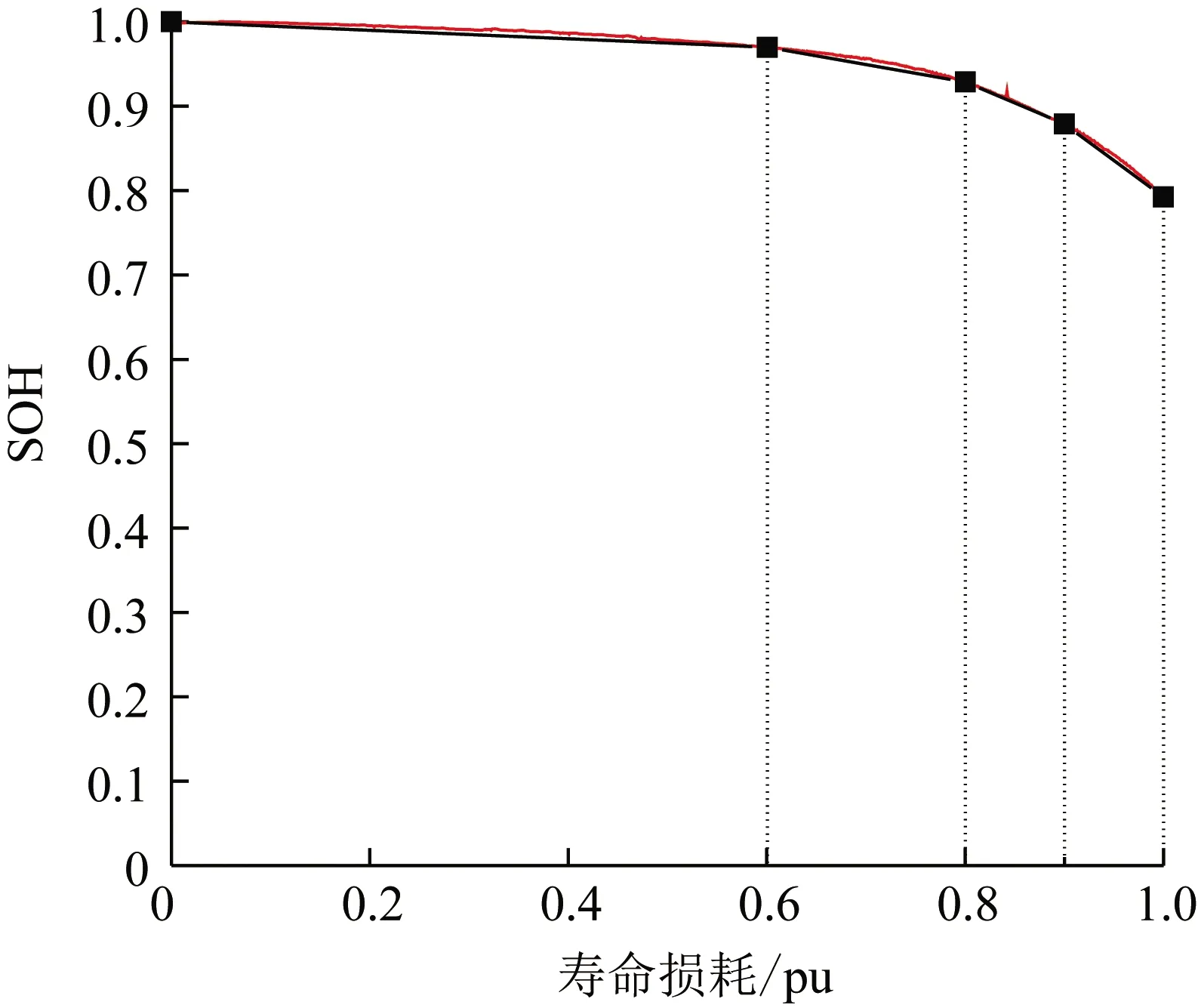
图4 储能电池全寿命周期多阶段SOH

表1 储能电池参数

表2 储能电池SOH分段参数

Nlife=2187 0e-1.957(1-SOC)

(54)

式中：SOC为储能电池荷电状态值。

遗传算法参数设置如下：种群规模为40，交叉率为0.8，变异率为0.2，精英数为2，最大迭代数为50。服务费为0.5元/(kW·h)。如图5和图6所示，通过K-means聚类得到5个典型日的光伏和充电负荷出力曲线，各典型日的概率依次为：0.154、0.308、0.215、0.154、0.169。并且将储能电池全寿命分为4个阶段,确定20个场景。算例的其他仿真参数如表3所示。

图5 4 MW光伏电站出力

图6 电动汽车充电负荷

表3 其他参数

4.2 算例分析

本文提出的光储优化配置模型在Matlab2018平台进行仿真，并使用Gurobi 9.0进行求解。

遗传算法的迭代过程如图7所示，结果逐步趋于稳定至第30次迭代，解收敛至8.87×105元，并经过多次迭代，未搜索到更优解。最终结果如表4所示：光储电站的最优光伏配置容量为529.93 kW，储能电池额定容量为1 008.88 kW·h，额定功率为619.84 kW，服务年限为14年。

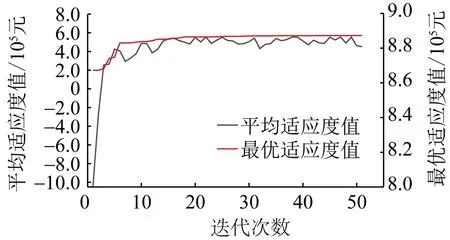
图7 遗传算法的迭代过程

表4 仿真结果

充电站的购电功率以及储能电池运行情况如图8所示(以典型日1为例)。由图8可知，在电价处于峰时(08：00—11：00和18：00—21：00)，储能电池多处于放电状态，电动汽车充电负荷由储能电池或光伏补充，充电站几乎不从电网购电，以减少充电站购电成本。当电网电价处于平谷时段时，购电功率高于充电负荷，储能电池处于充电状态，从电网储存能量用于峰时供给电动汽车充电负荷。并且，同一个典型日不同阶段的光储充电站最优运行模式区别较小，储能电池的工作模式均为“一充一放”，并且充电站购电功率曲线在各个阶段区别也较小，储能电池充放电状态在各个阶段一致，仅充放电功率略微有所区别。由此可知，储能电池老化速度以及容量衰减程度对同一典型日的运行策略影响不大。

图8 仿真结果

不同典型日的储能电池寿命损耗成本如图9所示，在储能电池的不同容量衰减阶段，由于光伏出力较低且充电负荷需求较高，典型日2和4的储能电池寿命损耗成本最高，相对而言，典型日3的充电负荷最小，对应的储能电池寿命损耗最少。各场景下储能电池容量衰减情况如图10所示，随着储能电池的不断使用，老化速度持续增高，以及SOH逐步降低，在相同寿命损耗程度下，储能寿命末期容量衰减程度明显提高，第4阶段日储能容量衰减量约是第一阶段的20倍。显然，随着储能电池的使用，其容量衰减速度不断提高。

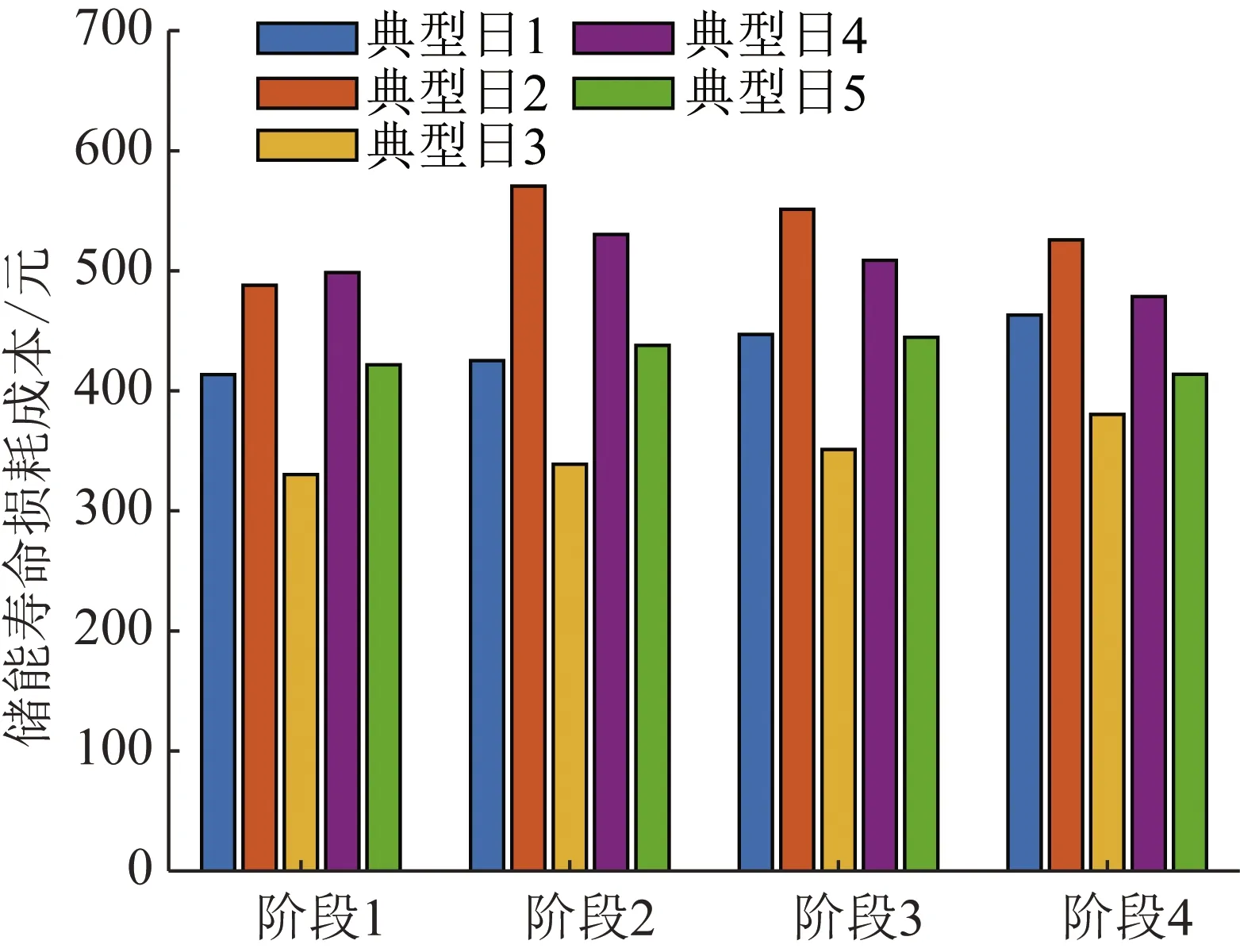
图9 储能寿命损耗成本

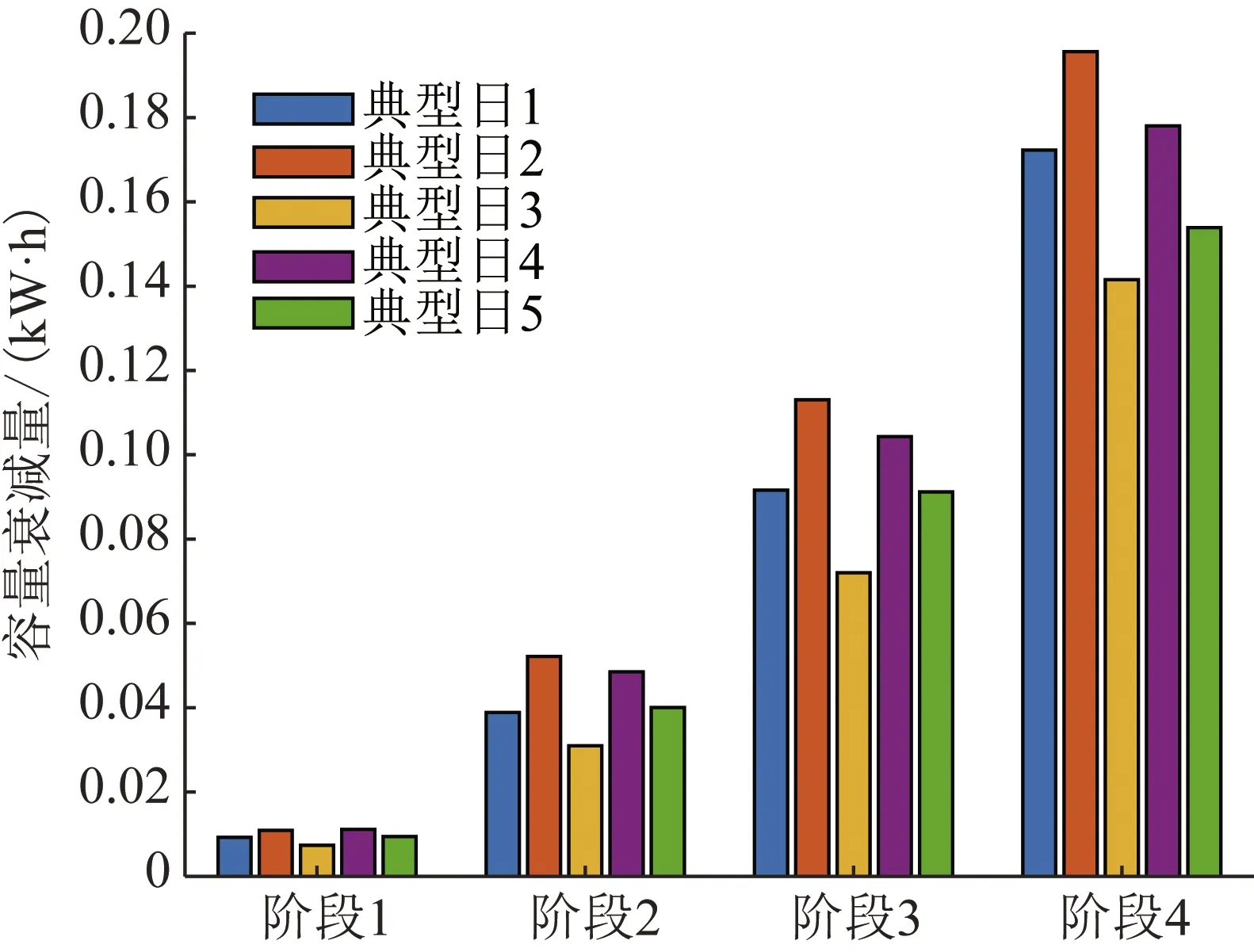
图10 储能容量衰减

为说明本精细化储能电池寿命损耗模型的意义，在其他参数保持一致的情况下，不考虑精细化储能电池动态模型的情况下，进行对比分析，结果如图11(以典型日1为例)和表5所示。由图11可知，由于考虑精细化储能模型的优化程序中，综合考虑了储能电池的寿命损耗、容量衰减情况，使得充电站更加经济高效地利用储能电池进行充放电。因此，未考虑精细化储能模型的结果劣于考虑精细化储能模型的结果。未考虑精细化储能模型算例的储能动作频次与幅度均高于考虑精细化储能模型的，充放电较为随意，充电站的运行情况未达到最优运行状态。如表5所示，未考虑精细化储能模型的年均收益为8.52×105元，比考虑精细化储能模型时低3.5×104元；并且储能电池的使用年限也仅为10.4年，比考虑精细化储能模型时少了3.6年，考虑精细化模型的储能电池的年均寿命损耗成本为1.63×105元，比未考虑时的降低5.6×104元。同时，未考虑精细化储能模型的年收益率也降低了0.34%，同样由于年均储能电池寿命损耗的增加，其SOH的衰减速度也在加快。由此可知，考虑储能电池精细化建模，能够降低储能电池寿命损耗成本，减缓容量衰减速度，增加使用年限，提升光储充电桩经济效益。

图11 未考虑精细化模型储能系统运行结果

表5 未考虑精细化储能模型算例结果

为研究光储系统的互补特性，分别仿真了未配置储能电池和未配置光伏的2个对比算例，结果如表6所示。未配置储能电池情况下，由于禁止充电站反送电至电网，会出现弃光情况，弃光率为9.3%。同时，缺少储能电池提供能量存储以及参与套利，不含储能电池的系统的收益比光储系统年均收益少了5.2×104元，但是，由于少了储能电池高额的配置成本，充电站年收益率却提高了4.62%。未配置光伏仅配置储能电池情况下，同样，充电站的年均收益为8.31×105元，低于光储联合运行充电站的收益，年均收益率为15.44%，高于光储联合运行的充电站的收益率。未配置光储系统的年均收益为7.28×105元。由此可见，同时配置光伏和储能电池确实可以提高电站的收益，但是，光储的高额配置成本导致收益率不高，随着光储的发展以及成本的下降，光储充电站经济价值将进一步提高。