考虑主动管理与需求侧管理的主动配电网分布式光伏最大准入容量计算方法

蔡秀雯，陈茂新，陈钢，方一晨，张沈习，程浩忠

(1.国网福建省电力有限公司泉州供电公司，福建省泉州市 362000；2.电力传输与功率变换控制教育部重点实验室(上海交通大学电气工程系)，上海市 200240)

0 引 言

近年来，光伏发电技术在政策鼓励下高速发展，分布式光伏在配电网中渗透率不断提高。然而，分布式光伏出力可能引起配电网潮流变化，影响电能质量[1]。因此，有必要考虑各电气指标约束，展开配电网分布式光伏最大准入容量的研究。

目前，国内外已有若干研究提出配电网分布式电源最大准入容量计算方法。文献[2]建立了以分布式电源并网容量最大为目标，考虑电压水平、旋转备用、线路功率、投资运行总费用等约束的分布式电源规划模型，采用随机权重粒子群算法进行求解；文献[3]计及电压偏差、电压波动、短路电流、继电保护约束，采用基于灵敏度的协调分段计算方法求解分布式电源最大并网容量；文献[4]建立了交直流混合配电网分布式电源最大准入容量计算模型，将其转化为混合整数二阶锥模型，直接调用求解器高效、准确求解，克服了启发式算法易陷入局部最优的缺陷。

实际上，分布式光伏功率与负荷功率具有不确定性，在分布式光伏最大准入容量计算中应予以考虑。文献[5]和[6]建立了基于机会约束的配电网分布式光伏最大准入容量计算模型；文献[7]采用蒙特卡洛抽样生成多场景，选取各场景下分布式光伏准入容量最小值作为最终结果；文献[8]使用盒式鲁棒区间表征“源荷”不确定性，使用鲁棒辅助变量替代不等式约束中的“源荷”功率变量，将模型转化为对偶形式后求解。

为应对大规模分布式光伏接入对配电网造成的不利影响，同时提升配电网对分布式光伏的消纳能力，传统配电网逐渐被主动配电网(active distribution network, ADN)替代。ADN可以对各种分布式资源进行综合控制[9]，电网侧应实现主动规划、管理、控制与服务，用户侧应积极参与需求侧响应，分布式电源侧应采用功率控制与调节技术，主动参与ADN的运行调度[10]。文献[8]将有载调压变压器(on-load tap changer, OLTC)与静止无功补偿器(static var compensator, SVC)应用于ADN中，建立了分布式光伏最大准入容量计算模型；文献[11]在使用OLTC与SVC的基础上，考虑了网络重构、分布式光伏功率调节、投切电容器组进行无功补偿等主动管理(active management, AM)措施，提高分布式光伏最大准入容量；文献[12]使用储能与智能逆变器增大分布式光伏准入容量；文献[13]验证了智能软开关对潮流的改善作用，可促进配电网分布式光伏消纳。

现有研究存在以下不足：1)多数研究并未计及“源荷”不确定性，模型的鲁棒性有待提高；2)多从电网侧角度提升配电网分布式光伏最大准入容量，但并未考虑用户需求侧管理(demand side management, DSM)的作用。本文将在储能投资限制下，优化ADN中储能配置，并考虑分布式光伏出力与负荷功率的不确定性，应用有载调压、无功补偿、储能调节、网络重构与负荷削减等AM与DSM措施，建立“源荷”不确定性场景下ADN分布式光伏最大准入容量计算模型，通过凸松弛技术将其转化为混合整数二阶锥形式，并使用列与约束生成算法进行求解。

1 “源荷”典型时序场景构建

分布式光伏出力与负荷功率具有季节周期性与日周期性的特点。为计算ADN中分布式光伏最大准入容量，需要构建“源荷”典型时序场景集，确保容量不高于计算结果的分布式光伏接入在各场景下均不会导致ADN电气指标越限。

聚类算法在场景生成方面得到广泛应用[14]。本文采用k-means聚类[15]生成“源荷”典型时序场景。k-means算法聚类结果会在较大程度上受到聚类数的影响。为避免聚类结果陷入局部最优，同时确保生成的场景具有典型性，使用CH(+)指标评价不同聚类数下的k-means聚类结果，选取CH(+)指标值最高时的聚类数K作为最佳聚类数[16]。

CH(+)指标计算公式为：

(1)

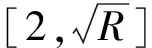
确定最佳聚类数K后，首先生成K个初始质心，将样本点划分到与质心距离最小的类中，形成K个簇，并计算、更新各个簇的质心，直至质心位置的变化量小于某一阈值，由此可构建“源荷”典型时序场景。考虑到“源荷”功率具有不确定性，以典型场景中各时刻“源荷”功率为基准，按一定偏移度设定区间，表征其功率可能的范围。

2 主动管理与需求侧管理建模

在ADN中，拟采用AM与DSM措施，提升分布式光伏最大准入容量。使用的AM措施包括有载调压、无功补偿、储能调节与网络重构，DSM措施为负荷削减。本节对上述AM与DSM措施进行建模。

2.1 有载调压

OLTC通常接在上级电网(节点0)与配电网首节点(节点1)之间，用于调控节点电压分布。支路0-1与OLTC的阻抗之和为r01+jx01。在节点0和节点1之间设置虚拟节点m，令支路0-m阻抗为r01+jx01，支路m-1接有零阻抗OLTC，则场景s时刻t下的OLTC数学模型如式(2)—(3)所示。

(2)

(3)

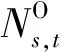
2.2 无功补偿

投切电容器组可用于无功补偿，其数学模型为：

(4)

(5)

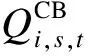
2.3 储能配置与调节

在配电网中安装储能模块，可通过对储能充放电状态与功率的调控，实现灵活性资源配置，增大ADN对分布式光伏的接纳能力。现考虑投资成本限制，对储能进行配置。储能投资约束为[17]：

(6)

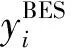
场景s时刻t下节点i的储能数学模型为：

(7)

(8)

(9)

(10)

(11)

在储能配置与运行优化中，需要确定待选节点上安装的储能模块数量，使之满足投资约束；同时，需要优化各场景下调度周期内储能的模拟运行策略，通过储能调节最大化ADN中的分布式光伏准入容量。

2.4 网络重构

ADN运行过程中，改变联络开关通断状态可调整网络拓扑。ADN应始终满足辐射状拓扑约束，ADN网络重构模型如下：

(12)

式中：N为ADN节点集合；N(i)为可能与节点i相连的节点集合；D为ADN支路集合；若节点j为i的父节点，则βij,s,t为1，否则βij,s,t为0；αij,s,t用于表征支路ij通断状态，0表示断开，1表示连通。

2.5 负荷削减

本文考虑的DSM措施为负荷削减，负荷由基本负荷与可削减负荷构成[18]。接于节点i的负荷于场景s时刻t下的模型为：

(13)

(14)

负荷削减数学模型如式(15)—(16)所示：

(15)

(16)

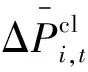
3 分布式光伏准入容量优化模型

3.1 目标函数

在最大化ADN分布式光伏准入容量时，应考虑“源荷”不确定性的影响，确保在不确定性最不利条件下ADN仍能安全、稳定运行。各典型场景中，“源荷”不确定性可用式(17)—(18)所示的鲁棒区间表示：

(17)

(18)

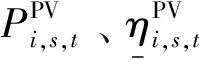
分别使用y和n表示待选节点接入的分布式光伏容量和储能模块数，分别使用zs,t、xs,t和as,t表示场景s时刻t下的配电网潮流变量、AM和DSM变量向量、“源荷”不确定性辅助变量向量。以最大化分布式光伏准入容量之和为目标，同时考虑“源荷”不确定性最不利条件对其抑制作用与AM、DSM技术对其提升作用，优化模型目标函数如式(19)所示：

(19)

式中：F为“源荷”场景给定时n和xs,t的可行域；U为as,t的可行域；Ψ为n、xs,t和as,t给定时y和zs,t的可行域；f为元素为1的列向量。

3.2 约束条件

除AM、DSM约束外，ADN分布式光伏最大准入容量计算模型还应考虑系统运行与安全约束。本节将对其进行建模。

3.2.1DistFlow方程约束

(20)

(21)

考虑网络重构后，潮流方程约束为：

(24)

(25)

(26)

(27)

式中：Pki,s,t、Qki,s,t分别为从节点k流向i的有功与无功功率；rki和xki分别为支路ki的电阻与电抗；Iki,s,t为流经支路ki的电流；Vi,s,t为节点i电压。

3.2.2支路电流约束

当支路ij联络开关断开时，电流为0，否则，支路电流应小于上限值。约束为：

(28)

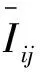
3.2.3节点电压约束

ADN节点电压约束为：

(29)

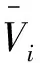
3.2.4电压波动约束

分布式光伏出力波动会引起ADN节点电压波动，对电能质量造成不利影响。电压波动及其约束为[20]：

(30)

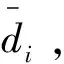
3.2.5谐波电流约束

分布式光伏注入并网点的谐波电流不应超出文献[22]规定的限值，其表达式与约束为：

(31)

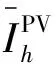
3.2.6主变压器传输功率约束

场景s时刻t下由上级电网经主变压器流入ADN首节点的有功功率P0m,s,t与无功功率Q0m,s,t应分别满足约束(32)和(33)：

(32)

(33)

4 原模型转化与求解

前文得到的优化模型含非线性项与绝对值项，难以直接求解。本节将原问题拆分为主问题与子问题，转化为混合整数二阶锥形式后，使用列与约束生成算法求解。

4.1 模型转化

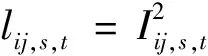
(34)

(35)

vi,s,t-vj,s,t-2(rijPij,s,t+xijQij,s,t)+

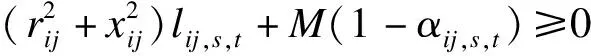
(36)

vi,s,t-vj,s,t-2(rijPij,s,t+xijQij,s,t)+

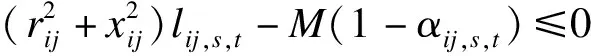
(37)

(38)

式中：‖ · ‖2为欧几里得2-范数；M为极大数。

约束(28)和(29)分别转化为：

(39)

(40)

OLTC约束(2)可转化为以下形式[24]：

(41)

(42)

(43)

(44)

(45)

(46)

为便于展现后续模型求解过程，将该二阶段鲁棒优化模型写成一般化形式GP，如附录A式(A1)所示。GP中的变量符号与具体变量的对应关系如附录A式(A2)所示。

4.2 模型求解

上文得到的优化问题目标函数包含两阶段。第1阶段对应外层max问题，即通过优化AM和DSM变量，最大化分布式光伏准入容量；第2阶段对应内层min-max问题，即考虑“源荷”不确定性对结果的抑制作用，通过最优化潮流确定最不利条件下分布式光伏最大准入容量。

包含两阶段的原问题可使用列与约束生成(column-and-constraint generation, C&CG)算法[25]求解。原问题被分解为主问题(master problem，MP)和子问题(sub-problem,SP)，分别如附录A式(A3)和(A4)所示。MP、SP目标函数值分别为解的上界(upper bound, UB)与下界(lower bound, LB)。主、子问题交替迭代求解，直至UB与LB之差低于设定阈值。

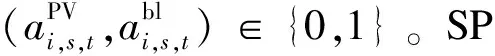
使用C&CG算法求解模型的步骤如下：

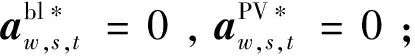
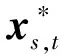
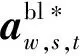
5)若上下界之差为UB-LB≤ε，停止迭代，输出结果；否则，返回步骤3)。

5 算例分析

5.1 算例设置

为验证前文所提模型与求解方法的有效性，本节将在改进的IEEE 33节点配电网系统上进行算例分析，基于MATLAB 2016a程序开发与仿真平台，采用YALMIP工具箱调用Gurobi 9.0.0商业求解器对模型进行求解。硬件配置为i5-10500 CPU、3.10 GHz处理器、16 GB内存。算例配电网如图1所示，线路阻抗与负荷参数详见文献[27]，各节点负荷功率因数恒定。节点3、7、10、14、27上负荷的可削减部分占比为30%，可全部或部分切除。

图1 改进的IEEE 33节点配电网

分布式光伏待选接入点为节点10、17和32，分布式光伏谐波电流频谱详见文献[28]，无功功率忽略不计[20]；OLTC正、负向各有4个挡位，调节范围在0.95～1.05 pu之间；投切电容器组接在节点15与28上，最大可投切5个电容器，单个电容器可补偿30 kW无功功率；拟于节点7处规划储能装置，单个储能模块额定功率为250 kW，额定容量为1 000 kW·h，充、放电效率为85%，经济使用年限为20年，贴现率为8%，单位容量造价为1 530元/(kW·h)，建设投资成本上限为54.4万元，荷电状态上、下限分别为80%和20%，调度周期始末时刻荷电状态为50%；支路12-22和18-33装有常开联络开关，支路4-5和13-14装有分段开关。

对全年分布式光伏出力与负荷功率进行k-means聚类，CH(+)指标在聚类数为3时取值最大。聚类数为3时，以分布式光伏装机容量与负荷功率历史最大值为基准值，“源荷”典型时序场景如图2所示。

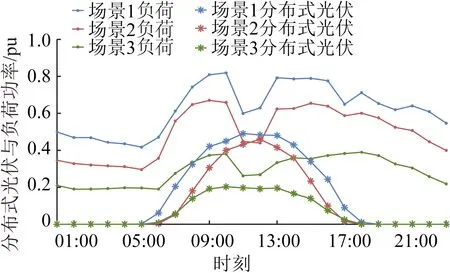
图2 “源荷”典型时序场景

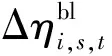
(47)

(48)

5.2 “源荷”不确定性对结果影响分析

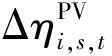
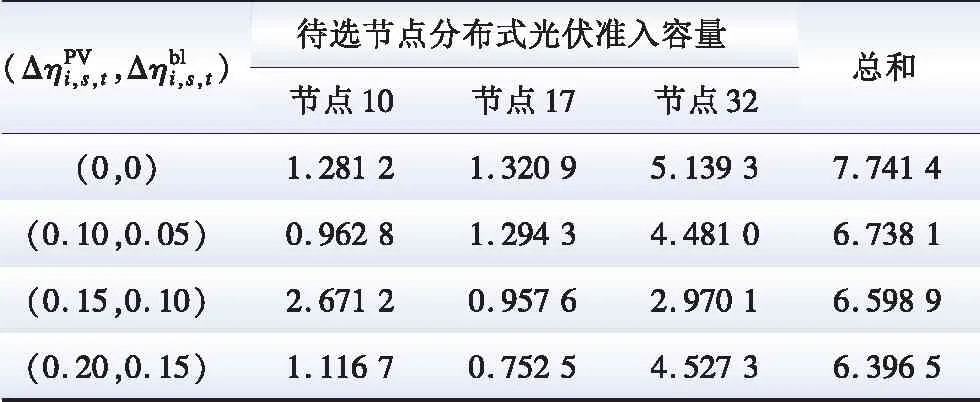
表1 不同鲁棒区间宽度下分布式光伏最大准入容量计算结果

5.3 主动管理与需求侧管理优化结果

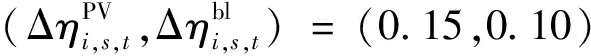
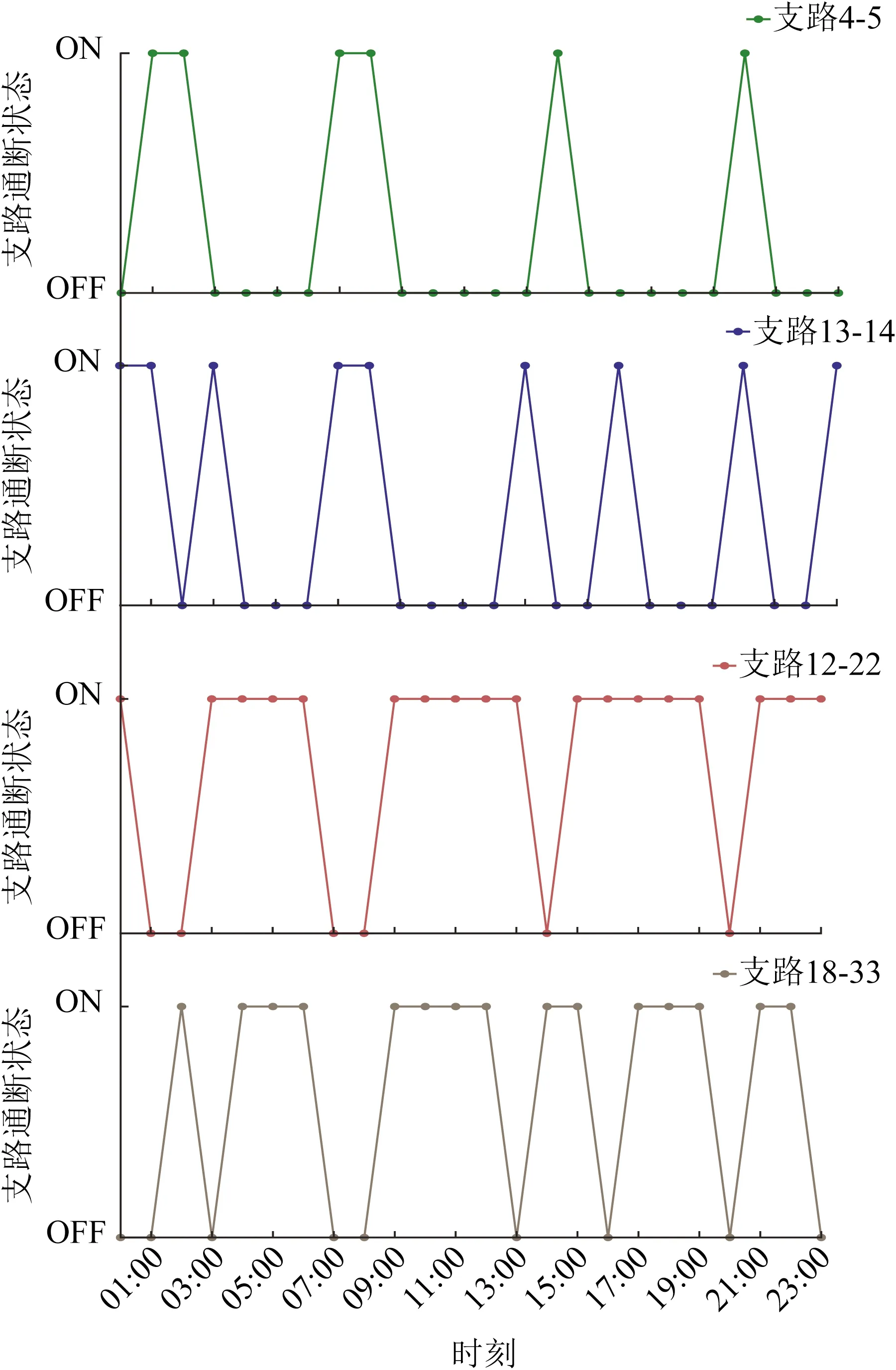
图3 支路通断状态

图4 储能荷电状态与充电功率

5.4 对比分析

为验证AM与DSM对ADN分布式光伏最大准入容量的提升作用，计算采用不同AM和DSM情况下的结果，如表2所示。由表2可知，场景1与场景4、5、2相比，分布式光伏最大准入容量分别提升了29.54%、13.60%和1.93%，则对于该算例配电网，储能调节对分布式光伏最大准入容量提升作用最大，网络重构和有载调压次之；无功补偿和负荷削减对分布式光伏最大准入容量的提升效果较弱。

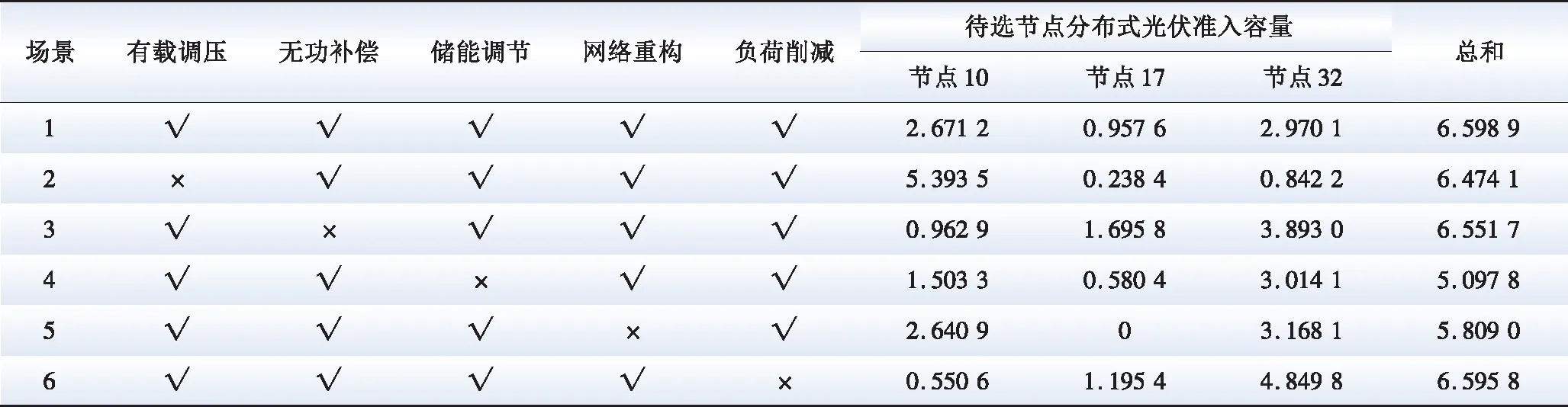
表2 不同AM和DSM组合下分布式光伏最大准入容量

节点3、7、10、14和27上的负荷含可削减部分，负荷削减情况如图5所示。

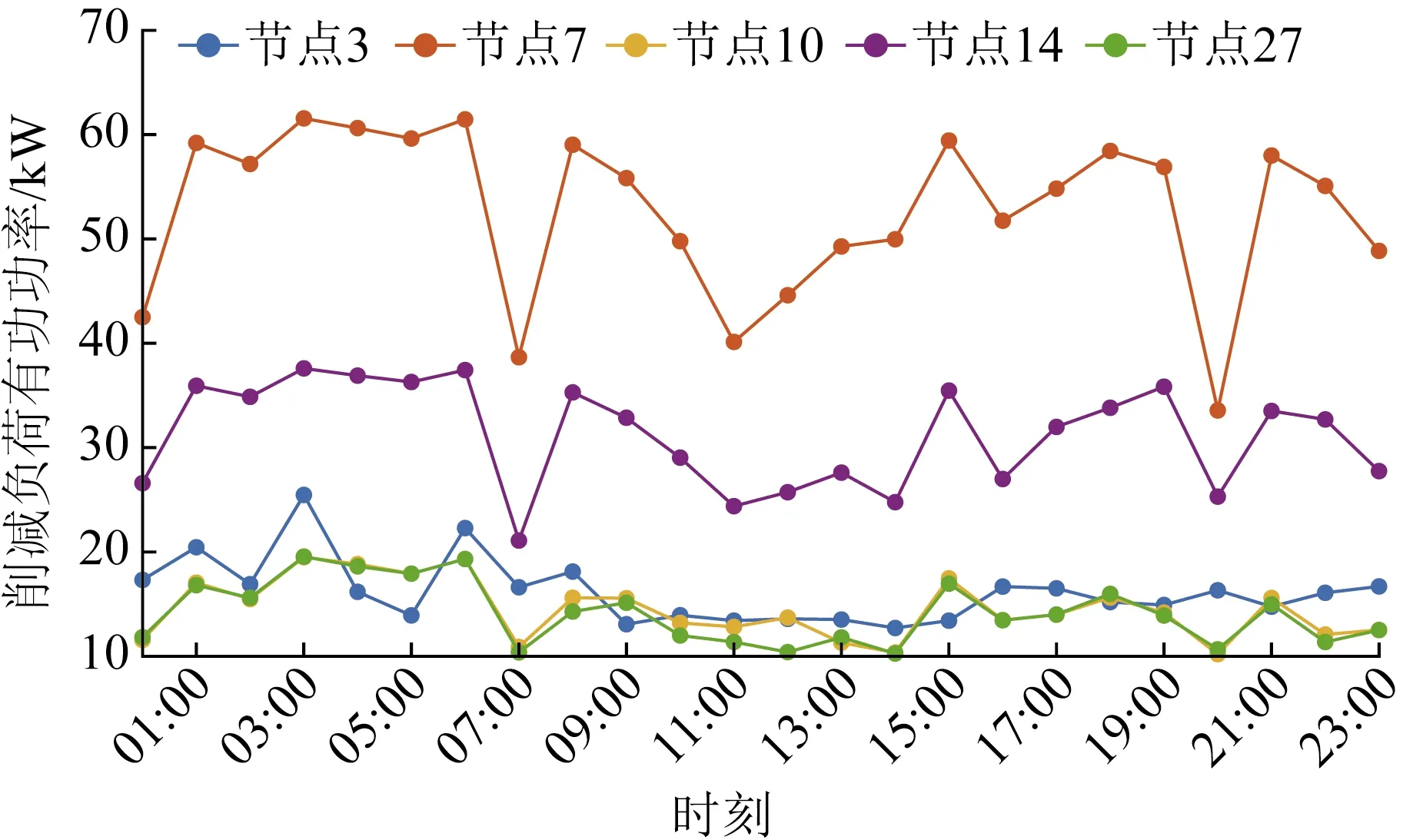
图5 负荷削减曲线

6 结 论

本文提出了考虑“源荷”不确定性、主动管理与需求侧管理的主动配电网分布式光伏最大准入容量计算模型，转化为具有混合整数二阶锥形式的主问题与子问题后，使用列与约束生成算法求解。算例分析表明，“源荷”不确定性可能对分布式光伏最大准入容量产生抑制作用，且抑制程度与鲁棒优化保守程度成正相关；主动管理与需求侧管理对分布式光伏最大准入容量具有提升作用，可有效促进分布式光伏消纳。在后续研究中，更多主动管理、需求侧管理措施与配电网的耦合机理仍待进一步深入探讨。