基于强化学习的建筑集群需求侧能量管理方法

2021-05-12安佳坤贺春光刘洪凌云鹏齐晓光李维宇孙鹏飞檀晓林

电力建设 2021年5期

安佳坤，贺春光，刘洪，凌云鹏，齐晓光，李维宇，孙鹏飞，檀晓林

(1.国网河北省电力有限公司经济技术研究院，石家庄市 050021；2.智能电网教育部重点实验室(天津大学)，天津市 300072)

0 引言

随着分布式能源技术的发展、可再生能源的高比例渗透以及中国电力市场化改革的不断推进，终端用户对电力系统运行状态的影响越来越大，而这也推进了需求响应业务向着多元化、常态化快速发展。对终端用户实施有效的能量管理能够在很大程度上提高电力系统的灵活性，根据国际能源署提供的报告数据，用户侧需求响应的潜力通常约占峰值需求的15%，而基于欧盟的统计数据，到2050年，用户的响应潜力可能超过150 GW[1]。因此，充分挖掘终端用户的用能特性与需求响应潜力也成为了当前研究的关键性问题。对电力公司而言，充分挖掘终端用户的用能特性与需求响应潜力可以更为准确地预测出多时间/空间尺度的负荷空间密度及总量分布，从而制定更为科学合理的规划与运行方案；同时，帮助更科学地制定动态能源价格与需求响应的激励政策，实现削峰填谷与节能减排。对终端用户而言，可以优化用能行为，降低用能成本；对社会而言，能够推动制造商有针对性地研发低能耗设备；同时，也能帮助监管部门科学地制定节能减排目标及相关政策。然而，终端用户种类多样、用能特性复杂、量测数据众多、能量交互信息量大，对用户的需求侧能量管理提出了新的挑战。传统的能量管理与调度过程易受到人员经验的影响；同时，终端需求侧能量管理过程中需要考虑的控制变量众多，传统数值迭代求解方法在一定程度上可能会受到维数灾难问题的限制。因此，如何利用人工智能技术发展更为智能的终端需求侧能量管理方法目前是亟待解决的重要技术问题[2]。

目前人工智能特别是强化学习算法在电力系统中的应用主要集中在故障监测与诊断[3]、负荷/功率预测[4-5]等方面，而对于需求响应与能量管理等更为深层次的研究与应用仍有待进一步探究。文献[6]总结了强化学习算法在建筑室内环境控制系统中的应用，并且分析了多智能体结合强化学习算法在建筑舒适控制中的应用。文献[7]对机器学习算法在建筑热舒适度预测模型中的应用进行了全面的总结与展望，并且提出了人工智能算法在建筑热舒适度控制中的应用。文献[8]分析了人工智能和大数据技术在商业/居民建筑设计和运营节能中的应用，并且验证了人工智能和大数据技术结合对建筑能效和成本效益的提升与改善作用。文献[9]提出了基于信息-物理-社会融合系统的智慧能源调度机器人群体及其知识自动化的关键理论方法，并给出了分散调度与集中调度模式下的平行建模与机器学习方法，为人工智能算法在调度控制中的应用建立了理论及可行性分析基础。文献[10]以综合能源微网作为研究对象，提出了基于多主体博弈与强化学习的并网型综合能源微网协调调度方法，探索了Q学习算法在综合能源微网调度运行中的应用，并验证了Q学习算法相较于传统启发式算法在算法性能方面的优势。文献[11]聚焦于电力系统的运行控制问题，以功率平衡、设备约束、电价趋势等作为主要依据，提出了一种基于关键状态变量变化率的动态分层强化学习方法。文献[12]基于前期负荷预测结果，充分利用隐含模式马尔科夫链与需求响应策略相结合的方式，为用户未来的用能方案提供决策与指导。文献[13]基于深度学习方法，通过对设备机组的状态空间进行有效调控，以提高多智能体微网系统运行的经济性与可靠性。

上述研究成果为本文的研究奠定了一定的理论基础，然而目前的研究存在以下问题：1)上述文献中涉及到的运行调度控制大多是针对系统或建筑整体层面的能量与功率进行调控，而未通过建立合理的建筑热平衡模型以进一步考虑用户侧的特性影响[7]。根据世界及中国相关建筑能源报告中的统计数据，建筑用能在能耗中的份额达到了近40%[14-15]，其中约一半用于满足温控负荷以及暖通系统的用能需求[16]，约20%用于满足热水负荷的用能需求[17]，而不同用户用能特性的互补往往可以提供更大的调度空间，因此，有必要通过建立建筑及典型灵活性负荷的精细化模型针对需求侧能量管理开展研究；2)以强化学习为代表的人工智能方法在需求侧能量管理及用户需求响应等方面应用的可行性仍亟待进一步探索。

针对上述问题，本文以建筑集群作为研究对象，提出基于强化学习的建筑集群需求侧能量管理方法。首先，以建筑集群为终端用能载体，构建建筑集群需求侧能量管理框架；其次，构建智能建筑R-C热平衡模型以及用户灵活性负荷模型，并结合Q学习算法，构建基于强化学习的需求侧能量管理模型；最后，通过实际仿真算例，对需求侧能量管理结果以及算法的性能进行对比分析。本文对强化学习在终端需求侧能量管理中的应用进行全面的探索。

1 建筑集群需求侧能量管理框架

本文所提出的基于强化学习的建筑集群需求侧能量管理整体框架如图1所示。本文以智能建筑作为终端负荷单元，以暖通系统和热水器作为主要灵活性可控负荷，不同功能(商业、工业、居民等)的智能建筑构成了可进行需求侧能量管理的建筑集群。每一栋智能建筑拥有相关的智能量测装置[18]，负责对智能建筑的灵活性负荷及刚性负荷需求进行计量，并将信息发送给地区能源服务商(regional energy service provider, RESP)进行集中处理。

图1 建筑集群需求侧能量管理整体框架

RESP在接收到不同功能建筑提供的负荷需求后，会充分利用不同功能建筑内不同类型负荷特性差异所带来的调度空间，同时考虑外部电网的实时价格信号，在保障用能需求及舒适度的前提下，以用能经济性最优为目标，通过挖掘不同功能建筑用能负荷之间的互补协调性、建筑本身的热耗散惰性以及热水器设备的热存储特性，实现对建筑集群需求侧的能量管理，向智能建筑下达负荷的供给及控制指令，从而有效提升建筑集群用户用能的经济性与合理性。

2 智能建筑及灵活性负荷建模

2.1 智能建筑热平衡模型

在实际的供冷或供暖场景中，智能建筑内部通常被模拟为单一等温的空调区域[19]，通常采用R-C网络模型对建筑内的单一制热/制冷区域进行建模[20]，建筑的R-C网络模型由热阻与热容构成，其中，热阻具有传输热的能力，连接智能建筑中的各个节点；热容具有存储热的能力，建筑中的各节点会经过热容接地。基于本文对建筑内部单一等温的假设，建筑整体模型则是由多个类似构造单一区域的聚合而成，并以此为基础，通过建筑暖通系统，调节系统送风温度与质量流量，从而实现对建筑内温度的集中控制。本文在文献[21]所介绍模型的基础上进一步改进与扩展，所构建的建筑R-C网络模型如图2所示。

图2 建筑R-C网络模型

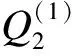
综合考虑建筑内产热与散热热源的关系，建立基于建筑R-C网络模型的室内热平衡方程为[22]：

(1)

(2)

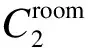
2.2 暖通系统模型

智能建筑中的暖通(heating, ventilation and air-conditioning，HVAC)系统主要负责调节室内温度，其能耗特性与室内外温度、智能建筑功能属性以及设备运行参数有关，暖通系统的主要结构模型如图3所示，图中ma为暖通系统内空气的质量。

图3 暖通系统结构模型

暖通系统运行造成室内温度的动态变化情况可参考式(2)中Q6，文献[24]已经对燃气-电力混合暖通系统及纯电力暖通系统两种典型的暖通系统的运行经济性进行了对比，本文以纯电力暖通系统为例，从能耗特性的角度，暖通系统消耗的电能PHVAC主要来源于两方面[25]：1)风扇进行新风空气循环消耗的电能PHVAC,f；2)暖通设备制冷/制热所消耗的电能PHVAC,h，以供暖期为例：

(3)

式中：ΔPeq,HVAC为等效总压降，计算方式为ΔPeq,HVAC=Pstatic+ρwv2/2，Pstatic为静压降；v为送风速度，本文中取4 m/s；ηHVAC,fan、ηHVAC,motor分别为风扇和发动机的运行效率，本文中二者的乘积取0.15。

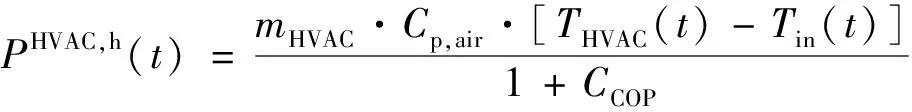
(4)

式中：CCOP为热电的能效比；Tin为室内温度，含义等同于式(2)中的T2。

综上所述，在单位调度时间段内，暖通设备消耗的电功率为：

PHVAC(t)=PHVAC,h(t)+PHVAC,f(t)

(5)

对暖通设备通常采用3种控制方法[26]：1)温度控制(T-控制)，即只对暖通设备的送出温度进行调节；2)流量控制(M-控制)，即只对暖通设备的空气流量进行调节；3)综合控制(I-控制)，即对暖通设备的送出温度与空气流量均可进行调节。后文将会具体分析对比不同调节手段对能量管理及运营效益的影响。

2.3 热水器模型

智能建筑中的热水器主要设备负责满足室内人员日常行为中对热水的需求，热水器设备的主要结构模型如图4所示。热水器的温度动态变化方程[27]如式(6)所示：

图4 热水器结构模型

(6)

式中：TWT(t)为t时刻热水器水箱内的温度；VWT为热水器水箱的容积；fv(t)为t时刻热水流出水箱的速率；Tin,WT(t)为进入水箱的冷水温度；PWT(t)为t时刻热水器的运行功率；ηWT为热水器的运行效率；T0(t)为t时刻的环境温度；AWT为热水器水箱的表面积；RWT为热水器的热阻；SWT(t)为t时刻热水器的开关状态，其中，运行时的取值为1，关闭时的取值为0；Δt为调度控制的时间间隔。

热水器设备的具体用能特性与温度、用水量等因素有关。本文假定进入智能楼宇的水温是10 ℃，且忽略地理地貌、建筑材料、环境因素对进入智能楼宇水温的影响，而热水负荷使用的水温通常设定为40～49 ℃[28]，因此，热水器设备的能耗特性为：

(7)

式中：VGPM,WT为热水器设备消耗水的体积；DWT(t)为用热水持续时间；cwater为水的密度；Cp,water为水的比热容。

综上所述，建筑在t时段内总的电功率为：

(8)

式中：H为建筑内暖通系统的总数；W为建筑内热水器的总数；PO(t)为t时段其他非灵活性用电负荷的功率。

地区能源服务商会基于地区内不同功能类型建筑集群在不同时刻的用能需求，制定终端HVAC系统、热水器设备及其他用能负荷的供能计划，在满足热舒适度及基本用能要求的基础上进一步挖掘可调度空间，从而提高运营效益。因此，从RESP对建筑集群内终端负荷进行集中控制的角度出发，式(2)所示的建筑功率平衡方程可以进一步表示为：

(9)

式中：g(x,u)及d为系统等式方程中的非齐次项；x为状态变量，代表建筑节点的室内温度、热水供应量以及其他非灵活性负荷的供给情况；u为系统等式方程中的控制变量，代表HVAC系统的供给空气温度、空气流速率以及热水器的供水量等；d为系统等式方程中的扰动项；y为系统等式方程中的输出项，代表经能量管理后不同功能建筑的室内温度、热水供应量以及其他非灵活性负荷的供给情况；A、B为系统参数。

3 基于强化学习的需求侧能量管理

3.1 建筑集群需求侧能量管理模型

考虑到本文的研究重点是探究强化学习算法在建筑集群需求侧能量管理中的应用，因此，地区能源服务商在对建筑集群进行需求侧能量管理的过程中，考虑的管理目标是使得建筑集群用能的经济性最优，需求侧能量管理目标函数的具体表达式如下：

(10)

式中：EB为建筑集群的用能成本；pe(t)为t时段的分时电价；t0为调度起始时刻；T为能量管理调度周期。

地区能源服务商在对建筑集群进行需求侧能量管理的过程中，需要考虑以下约束条件：

1)建筑室内热平衡约束。

RESP对建筑集群的需求侧能量管理需满足式(2)所示的室内柔性负荷约束。

2)建筑室内温度舒适度约束。

本文基于《热环境的人类工效学》通过计算PMV和PPD指数与局部热舒适准则对热舒适进行分析测定与解释(GB/T18049—2017)，采用预计的平均热感觉指数(predicated mean vote, PMV)和预计不满意者的百分数(predicated percentage of dissatisfied, PPD)[29-30]评价热舒适度等级，划分结果如表1所示。

表1 热舒适度等级划分

在供暖季，选择偏冷(PMV介于-1到0之间)的环境，对应PMV为0时的温度上限为24 ℃。在供冷季，对于I级用户，应保持室内相对湿度在40%～70%之间，PMV值在0～0.5之间；同理对于II级用户，经过热舒适区的计算，所得舒适温度的范围为27～28 ℃。

3)设备调节约束。

在对建筑集群的需求侧进行能量管理的过程中需要满足HVAC系统及热水器设备的相关运行约束：

0≤mHVAC≤mHVAC,max

(11)

THVAC,min≤THVAC≤THVAC,max

(12)

PWT,min≤PWT(t)≤PWT,max

(13)

TWT,min≤TWT≤TWT,max

(14)

式中：mHVAC,max为HVAC系统送风质量流量的最大值；THVAC,max和THVAC,min分别为HVAC系统送风温度的最大值与最小值；PWT,max和PWT,min分别为热水器设备运行功率的最大值与最小值；TWT,max和TWT,min分别为热水器设备水箱内温度的最大值与最小值。

3.2 Q学习算法的基本原理

Q学习算法[31]是目前常用的强化学习算法之一，也是一种基于值函数迭代的在线学习和动态最优技术。其主要原理是将之前训练过的带有训练经验的Q值表作为后续迭代计算的基础，从而缩短算法的收敛时间。Q学习算法的值函数及迭代过程分别为：

(15)

Qk+1(sk,ak)=Qk(sk,ak)+α[R(sk,sk+1,ak)+

(16)

式中：s与s′分别为当前状态和下一时刻的状态，其含义对应于式(9)中的变量x；R(s,s′,a)为状态s经过动作a转移到状态s′后得到的立即奖励函数值，其中，变量R的含义对应于式(10)所示的目标函数，变量a的含义对应于式(9)中的变量u；γ(0<γ<1)为折扣因子；p(s′|s)为状态s在控制动作a发生后转移到状态s′的概率；Qk为最优值函数Q*的第k次迭代值；α为学习因子，表征要基于改善更新部分的信任程度；Q(s,a)为s状态下执行动作a的Q值。

在实际迭代的过程中，需要依据当前状态选择接续的控制动作，以更新Q值表。目前对于动作被选取概率计算与确定方面的研究通常采用贪婪策略[32]与轮盘赌策略[33]等。然而，采用贪婪策略将无法充分利用已有经验对动作空间进行搜索，易出现局部最优收敛的情况；另外，轮盘赌方法由于需要额外进行二进制转换以获取动作被选取概率信息，会在无形中增加一部分计算量。因此，基于上述考虑，本文采用Boltzmann概率分布法来刻画进化博弈中的状态转移概率。Boltzmann概率分布法是通过概率来选择行动，在状态s时选择行动ai的概率为：

(17)

式中：A′为控制动作集合；λ为进化博弈时段k(重复博弈的迭代数)的函数，具体为：

λ=5×0.999 9t

(18)

λ变量刻画了智能体决策的随机性。当λ增大时，智能体决策的随机性也随着增大；而当λ减小时，决策的随机性变小。由此可见，Boltzmann概率分布法与Q学习算法结合起来具有自适应学习的能力。

3.3 基于Q学习的需求侧能量管理流程

基于前文构建的智能建筑、灵活性负荷以及需求侧能量管理模型，结合Q学习算法，本文所提出的基于强化学习的建筑集群需求侧能量管理调控流程为：

步骤1：初始化Q值表。

初始化规则为线下预学习阶段Q值表中各元素(s,a)的初值均取为0；在线学习阶段将其初值化为预学习保留的可行Q值表。

步骤2：将连续状态和动作变量离散化，构建<状态，动作>对值组合。

离散化的主要目的是配合Q学习算法进行学习，对结果精度产生影响可忽略不计。通过马尔可夫模拟产生样本，结合需求侧能量管理目标函数，选取当前所属的运行状态并根据当前状态结合行动选择概率确定当前行动策略。

在状态空间的选取部分，本文将各时段内的室内温度、热水供应量以及其他非灵活性负荷的供给情况作为状态输入。上述变量均为连续变量，为配合Q学习方法，将上述变量离散化为区间形式，根据建筑集群实际的负荷需求情况即可唯一确定所属状态sk=，其中，sHVAC为HVAC系统的状态，具体表征此时的室内温度；sWT为热水器设备的状态，具体表征此时的热水供应量；sLoad为建筑集群内非灵活性负荷的状态，具体表征非灵活性负荷的用能需求。

同理，在动作空间的选取部分，本文中动作策略包括HVAC系统的供给空气温度、空气流速率以及热水器的供水量。上述变量均为连续变量，为配合Q学习方法，同样离散化为区间的形式。根据建筑集群实际的负荷需求情况即可唯一确定的动作策略ak=，其中，aHVAC.T为HVAC系统供给空气温度的动作策略；aHVAC.m为HVAC系统空气流速率的动作策略；aWT为热水器设备供水量的动作策略。

将可能的状态动作组合指令进行校验，剔除不满足约束的状态动作组合，在确定了迭代k的状态空间sk以及动作策略ak后，即可计算不同智能体所属时段的Q值。

步骤3:Q学习算法中奖励值的计算与式(10)相对应；同时，对未来的状态s′进行预测。

步骤4:得到未来的状态s′，根据Q学习方法的迭代公式对Q值表进行更新，并令s←s′。

步骤5:判断学习过程是否收敛，判断标准考察Q值表是否趋近于收敛；或者已经达到给定的学习步数或时间限制。若不收敛则令k=k+1，返回步骤2。

基于强化学习的需求侧能量管理方法的流程如图5所示。

图5 基于强化学习的需求侧能量管理流程

4 算例分析与对比

4.1 算例概况

本文将改进的IEEE 33节点配电系统作为建筑集群依附的主体配电系统结构，配电系统内的部分节点接有包含不同功能的智能建筑集群[34]，具体架构如图6所示。不同建筑集群内的具体建筑类型、建筑功能等信息如表2所示。

图6 算例系统架构

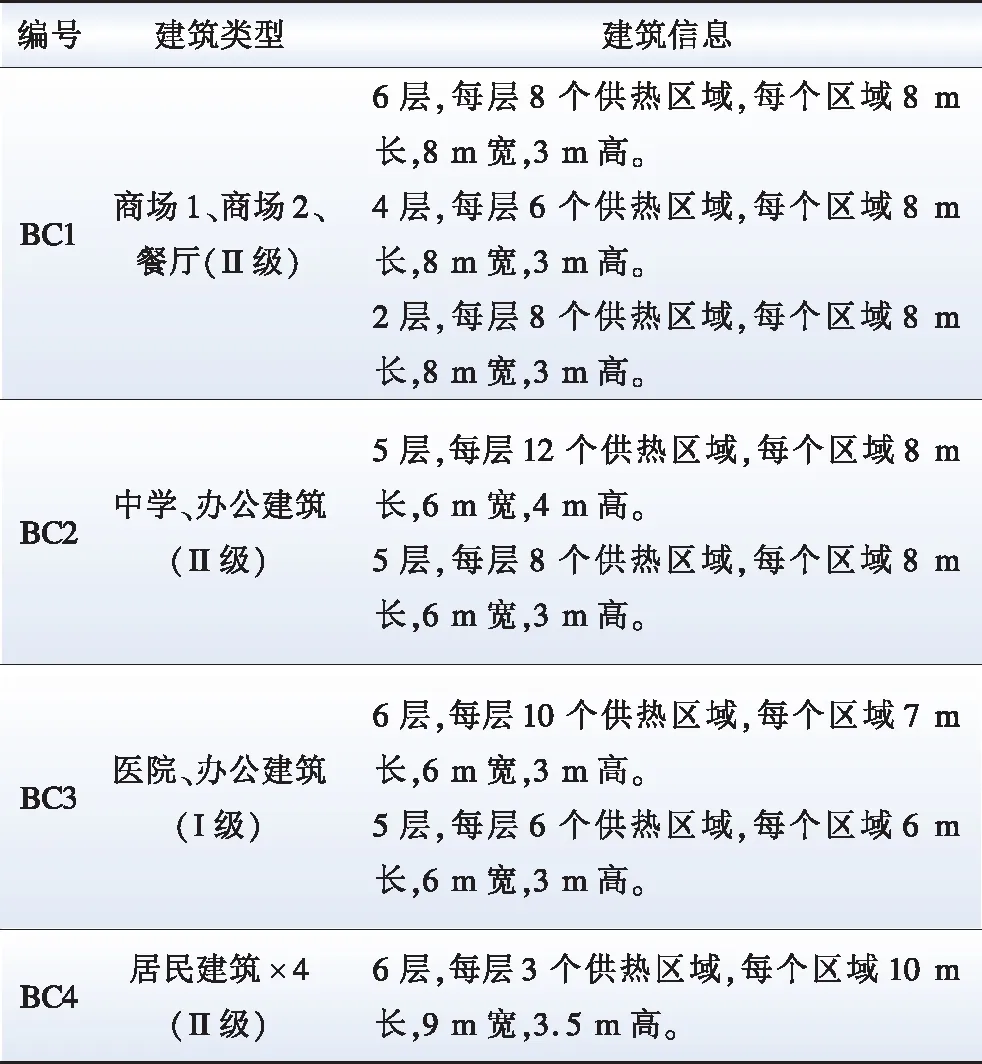
表2 建筑集群信息

建筑集群内的建筑均为独栋建筑，对于同一建筑集群内的不同智能建筑，RESP会根据建筑的供热等级采取相同的暖通及热水负荷的控制策略。建筑及HVAC系统的相关参数分别如表3及表4所示[24,35]。不同建筑集群在不同终端需求侧能量管理情况下的典型日负荷曲线如图7所示，地区不同时刻的分时电价如图8所示。

图7 不同建筑集群典型负荷曲线

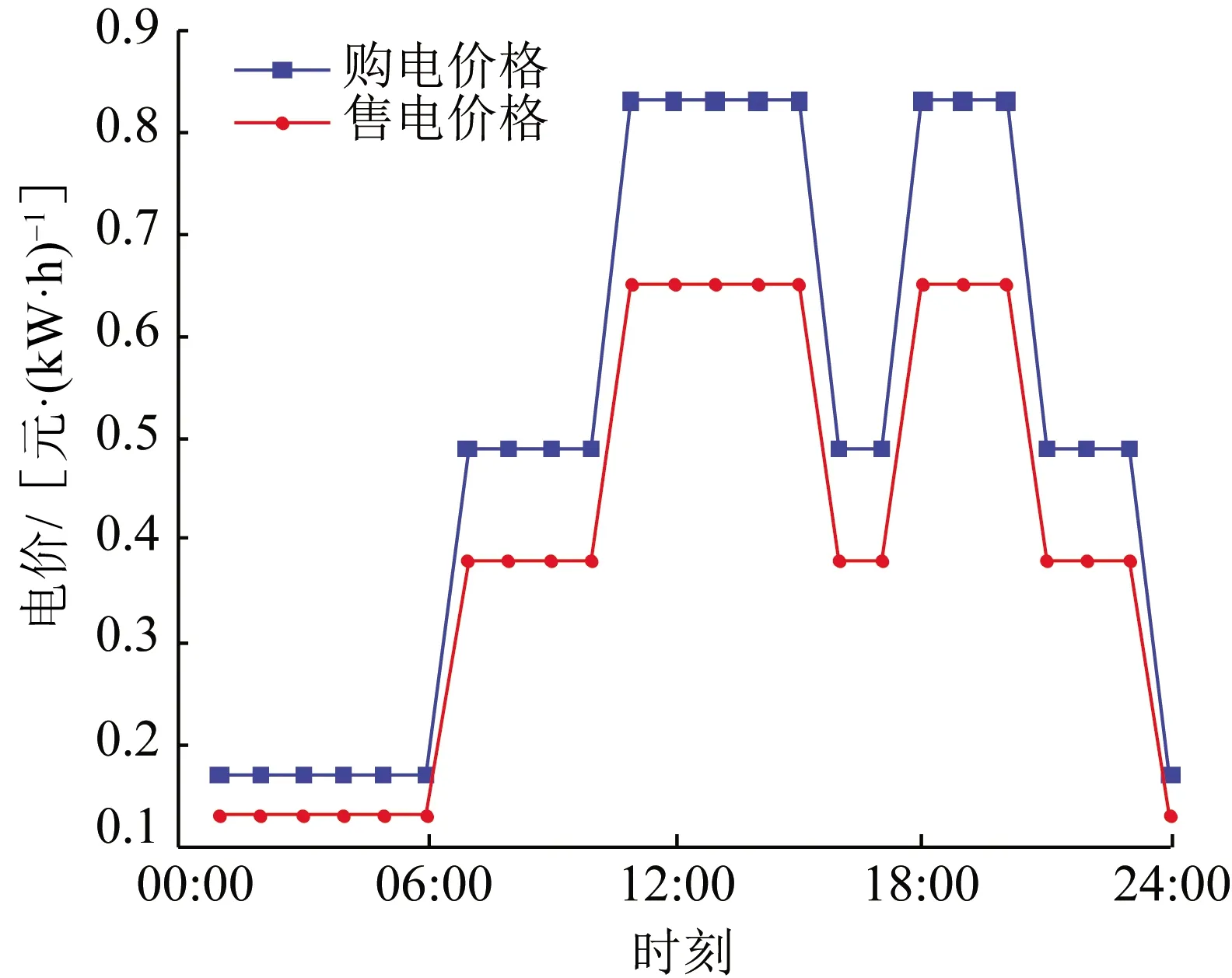
图8 地区分时电价

表3 建筑参数

表4 暖通系统参数

4.2 需求侧能量管理分析

基于算例设置，本文对不同建筑集群的需求侧能量管理结果进行分析，其中，调度时间步长Δt=1 h，通过对数据进行近200次的线下学习与仿真，不同建筑集群的需求侧能量管理结果如图9所示，通过结果图可以看出，需求侧能量管理可以有效实现负荷的“削峰填谷”。

图9 建筑集群需求侧能量管理结果

以BC1为例，在HVAC运行方面，由于BC1内的建筑均为II级建筑，因此HVAC系统会以节约用电作为主要运行目标。在01:00—05:00时段，由于用户处于休息状态，因此，HVAC系统会选择将温度维持在一个较低的水平；在06:00—07:00时段，由于临近工作时间，且购电电价较低，因此，HVAC系统会选择通过增加功率以提高室内温度；在08:00—09:00时段，由于购电成本升高，HVAC系统会适当减小出力，室内温度有所下降，然而，由于建筑的虚拟储能特性，室内温度仍能够满足温度约束条件；在10:00—12:00时段，随着室外温度的升高，阳光辐射的增强以及人体、机器散热等室内热源的辅助作用，室内温度不断升高并达到一天内的最高温度，此时HVAC系统会减小出力以节约用电成本；在13:00—16:00时段，随着室外温度的降低，室内温度也会逐步降低，然而，由于建筑的虚拟储能特性，此时室内的温度仍能够满足约束条件，HVAC系统仍可以通过降低出力节约电能使用；在17:00—24:00时段，HVAC系统会逐渐增加出力以保证室内的温度满足约束条件，然而，由于用户逐渐进入休息状态，因此，从节能的角度考虑，HVAC系统会将室内温度维持在较低水平。除此之外，RESP通常会选择在电价较低时刻满足用户的热水负荷需求。

由于建筑集群均是以运行经济性最优作为能量管理目标，因此其他建筑集群与BC1的管理策略类似，在此不再赘述。然而，由于BC3内的建筑均为I级建筑，对室内温度的要求相对较高，因此，HVAC系统始终需要将室内温度维持在较高的水平，相比较于其他建筑集群，通过能量管理的效果不如其他建筑集群明显。

在经济性方面，不同建筑集群在进行需求侧能量管理前后的日用能成本对比如表5所示。通过对比分析可知，采用需求侧能量管理，不同的建筑集群分别能够节省约18%、12%、6%、21%的用能成本。因此，通过对建筑集群进行需求侧能量管理，可以在一定程度上提升用户的经济效益，同时，相比较于以牺牲用户舒适度为代价的传统HVAC系统恒温调度方法，本文所提出的模型充分考虑了不同类型用户对于温度舒适度的需要，也提高了潜在的社会效益。综上所述，Q学习算法能够通过不断探索试错，积累一定的经验，从而具备实现建筑集群需求侧能量管理的能力。

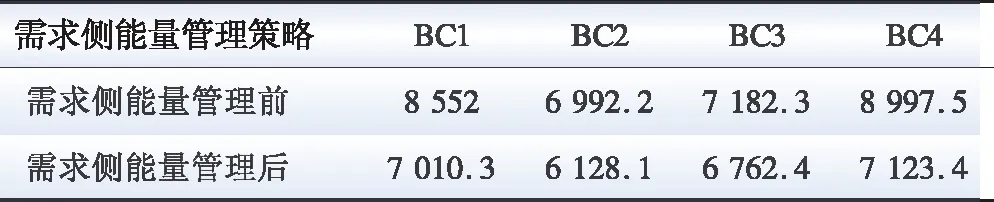
表5 不同建筑集群日用能成本对比

4.3 灵敏性分析

4.3.1控制方法影响分析

如2.2节所述，暖通系统包括3种控制方式，即温度控制(T-控制)、流量控制(M-控制)与综合控制(I-控制)，在不同控制方法下，暖通系统的电能消耗如表6所示。

表6 不同控制方法暖通系统能耗对比

通过对不同控制方式下暖通系统的能耗结果分析可知，在同样能够满足建筑用户热舒适度的前提下，相比较于对暖通系统实施送风温度或空气质量流量的单一控制方式，采用综合控制方法可以最大程度地配合建筑的相变虚拟储能特性挖掘暖通系统的节能与可调空间，从而实现节能安排与降低用能成本的目标。

4.3.2算法性能分析

本节选取传统启发式算法中的量子粒子群算法[36]，通过优化暖通系统及热水器设备的相关参数使得建筑集群日能耗成本的经济性最优，并与本文介绍的Q学习方法进行对比，基于4.1节提出的在线学习环境，以图6所示的BC1的日运行能耗成本为例，不同算法的迭代运行过程如图10所示。

图10 不同算法迭代过程对比

由图10可知，对于算例涉及的多变量优化问题，启发式算法需要相对漫长的搜索过程，需要约300次迭代会进入收敛范围，在线优化耗时387.3 s，另外算法容易陷入局部最优；而经过了预学习过程的Q学习方法通过学习经验可以直接将状态动作的搜索空间定在最终解附近，再通过深入挖掘得到最终的需求侧能量管理策略，通过约150次迭代即可收敛，在线耗时108.6 s，在算法效率与最优结果的挖掘方面均具有一定优势。