多维公平测度下考虑灾民心理痛苦效应的应急资源调配*
2021-05-12宋英华马亚萍李墨潇
宋英华,黄 茜,马亚萍,李墨潇
(1.武汉理工大学 中国应急管理研究中心,湖北 武汉 430070; 2.安全预警与应急联动技术湖北省协同创新中心,湖北 武汉 430070; 3.武汉理工大学 安全科学与应急管理学院,湖北 武汉 430070)
0 引言
大规模灾害发生后,灾民的生理和心理受到创伤,需要将大量应急物资运输到受灾区域用以救援活动的开展,因此应急资源分配和路径规划是灾后救援响应的关键环节,而灾后初期往往资源稀缺且运力有限,物资的不公平分配和服务时间的差异性均可加剧灾民生理和心理痛苦。因此如何高效而公平地进行应急调配决策,有效开展救援工作,减轻灾民的痛苦,是目前应急物流应该解决的重点任务。
目前国内外学者对灾害下应急救援资源管理进行了大量有意义的探索,早期侧重于资源分配和车辆路径研究,张广胜[1]借鉴Multi-Agent方法提出动静态资源共享的应急调度决策方案;Tlili等[2]提出考虑伤员分级的救护车救援路径优化模型;宋英华等[3]、Chai等[4]研究车辆等待和排队延迟情况下的应急资源调度方法;Ruan等[5]提出考虑不同救援参与者的应急资源联运策略,但均无考虑资源短缺情况下的公平性决策。针对公平视角下的应急资源调配问题,曲冲冲等[6]以最大化最小物资满足率为决策目标实现应急物资分配的公平性;詹沙磊等[7]以需求满足的误差率为公平指标研究配送效率和救灾分配公平问题;吕伟等[8]结合软硬时间窗约束对3种公平分配策略进行探讨;陈刚等[9]构造嫉妒函数和比例公平约束量化物资分配公平;在实际救援中,考虑到人的有限理性,应急主体的心理效应对应急调配方案决策的影响不可忽略,朱建明等[10]、曹庆奎等[11]、袁嘉杉等[12]引入前景理论刻画灾民和决策者对物资到达时间的风险感知,构建了考虑心理风险感知的应急资源调配模型;Sheu[13]根据生存心理和认知理论,建立以需求为导向的幸存者感知态度概念模型,提高幸存者的抗灾能力。综上所述,已有研究通常从物资数量单维度刻画公平性,缺乏对灾民理性需求和非理性感知的综合研究;国内外学者对于灾民心理感知的研究较少,由于灾害环境的复杂性,借鉴经济学、行为科学等跨学科理念的交叉融合,建立更符合现实系统的多因素心理感知模型亟待深入研究。
鉴于此,本文综合考虑物资短缺类型、数量和救助时间等多类感知因素,建立灾民心理痛苦效应函数,结合攀比函数和比例公平约束测度应急资源调配的公平性,构建“多配送中心—多灾点”的应急资源分配-路径规划决策模型;根据模型特性设计算法验证其有效性,以期为灾后应急资源调配寻求更高效的决策方案。
1 问题描述与假设
应急资源调配的多目标模型中,应急物流网络表示为无向图G=(N,A),N包括2个子集:受灾点集合I和配送中心集合B;A为连接边的集合,表征物资调配路线,(i,j)∈A;应急资源调配网络如图1所示,受灾区域内多个配送中心对多个灾点展开救援,应急车辆对多种类型物资进行配送。需要决策的问题是:在供需不平衡条件、车辆容量和时间窗限制下,选择合适的应急资源分配方案和车辆服务路线,使得应急资源调配总时间最短、公平性最高和灾民心理痛苦效应最小。
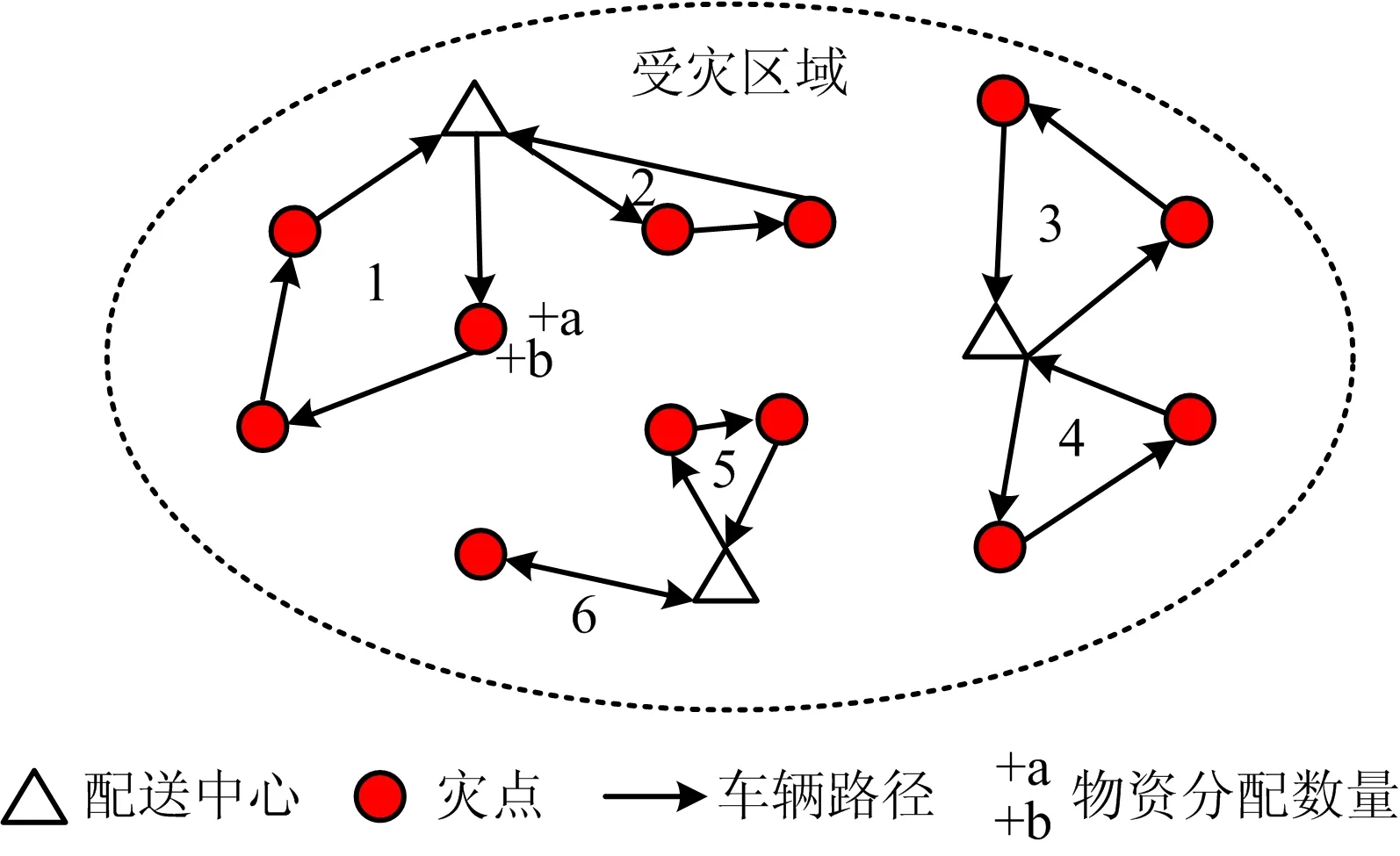
图1 应急资源调配网格Fig.1 Network of emergency resource allocation
模型假设如下:
1)配送中心和受灾点之间的供需量已知;
2)各类应急物资可混装,但不同种类应急物资之间不存在替代效用;
3)配送中心和受灾点之间的道路互相连通,应急车辆同时出发,受灾点有等待时间限制;
4)考虑车辆部分装载的情形;
5)不允许拆分配送。
2 模型建立
2.1 灾民心理痛苦效应
对于受灾群体而言,缺乏救援物资或等待服务的时间越长,所遭受的痛苦越大[14]。本文借鉴福利经济学中匮乏成本的定义来刻画灾民痛苦,考虑物资类型、物资数目、匮乏时间等多方面因素对灾民心理的影响,创新地提出救援过程中导致灾民心理痛苦的2种心理效应:1)等待效应,表示灾民因等待救援物资而产生态度、行为等方面的变化,使灾民痛苦上升;2)短缺效应,表示从开始到救援活动结束时,灾点仍供应不足,使灾民痛苦累积。引入文献[15]提出的幂函数量化心理效应,建立考虑2种效应的灾民心理痛苦效应模型,如式(1)~(2)所示:
(1)
(2)
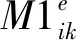
2.2 多维公平测度
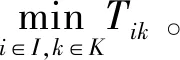
(3)
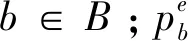
2.3 模型构建
基于以上建模分析,综合考虑救灾时效性、公平性和灾民心理痛苦效应,构建应急资源分配-路径选择决策模型。灾害发生后,要满足的首要目标即最小化运输总时间,如式(4)所示:
(4)
式中:Z1为运输总时间,h;tij为车辆从节点i到节点j的行驶时间,h;yijk为0~1变量,yijk=1时车辆k从点i开往点j,否则yijk=0。
为避免物资配送不及时,导致灾民的非理性行为,设置最小化时间攀比公平目标如式(5)所示:
(5)
式中:Z2为时间攀比值,h。
最大程度的缓解灾民因等待服务和缺乏物资造成的心理痛苦是应急资源调配的决策目标之一,设置最小化灾民痛苦心理效应目标如式(6)所示:
(6)
式中:Z3为灾民心理痛苦效应;ρ1和ρ2为2种心理效应的重要程度。
各受灾点物资到达时间的计算约束如式(7)所示:
(7)
各灾点救援时间窗约束如式(8)所示:
Tik≤TWi,∀i∈I,k∈K
(8)
式中:TWi为受灾点i的等待救援时间窗,h。
救援活动结束的时间计算约束如式(9)所示:
(9)
应急物资供不应求约束如式(10)所示:
(10)
应急物资供应量不高于配送中心储备量约束如式(11)所示:
(11)
为保证各灾点物资分配公平性,设置最低满足率约束如式(12)所示:
果然,我爬到窗户口看到了刘佳,他来送昨天我妈塞在他手里的钱,我妈拼命说我不懂事,又拼命把刘佳夸成了一朵花,让他跟我一块玩,好让我也变得听话些。
(12)
运输车辆容量限制约束如式(13)所示:
(13)
式中:q为车辆的装载量,t。
配送中心可对多个灾点进行物资配送,但每个灾点仅能接受1辆车的物资供应约束如式(14)~(15)所示:
(14)
(15)
决策变量路径选择和应急物资分配量的类型约束如式(16)~(17)所示:
yijk∈{0,1}
(16)
(17)
3 模型求解
本文构建的多目标应急资源调配模型属于非线性混合整数规划,模型变量和约束条件较多快速增加了求解的复杂性,多个决策目标往往是益损悖反关系,因此不存在满足所有目标的唯一最优解。针对所构模型综合考虑,设计第2代非支配排序遗传算法(NSGA-Ⅱ)[16]进行求解,具体算法步骤如下:
1)初始信息预处理。收集灾情信息,确定供需量,从百度地图提取路径距离和经纬度坐标。
3)计算适应度函数值。将目标函数转化为对应的适应度函数。按照最低满足率对配送中心负责的受灾点进行物资分配,计算物资是否全部分配;根据受灾点服务顺序确定路径方案,计算路径方案是否满足车辆载重限制和时间窗约束;计算各灾点的物资分配数量、到达时间和路径总时间,进而得到符合约束条件的3个适应度函数值。
4)非支配排序。采用精英策略,将种群进行非支配排序,当所有个体都有非支配层级时,停止排序。
5)选择、交叉和变异。根据4)的结果,基于拥挤度比较算子,对种群进行二元锦标赛选择操作。设置交叉和变异概率,采用PMX交叉法和边界变异法对种群进行交叉和变异操作,产生新的种群。
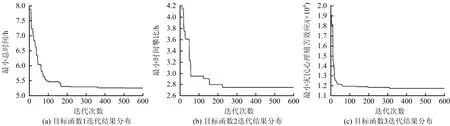
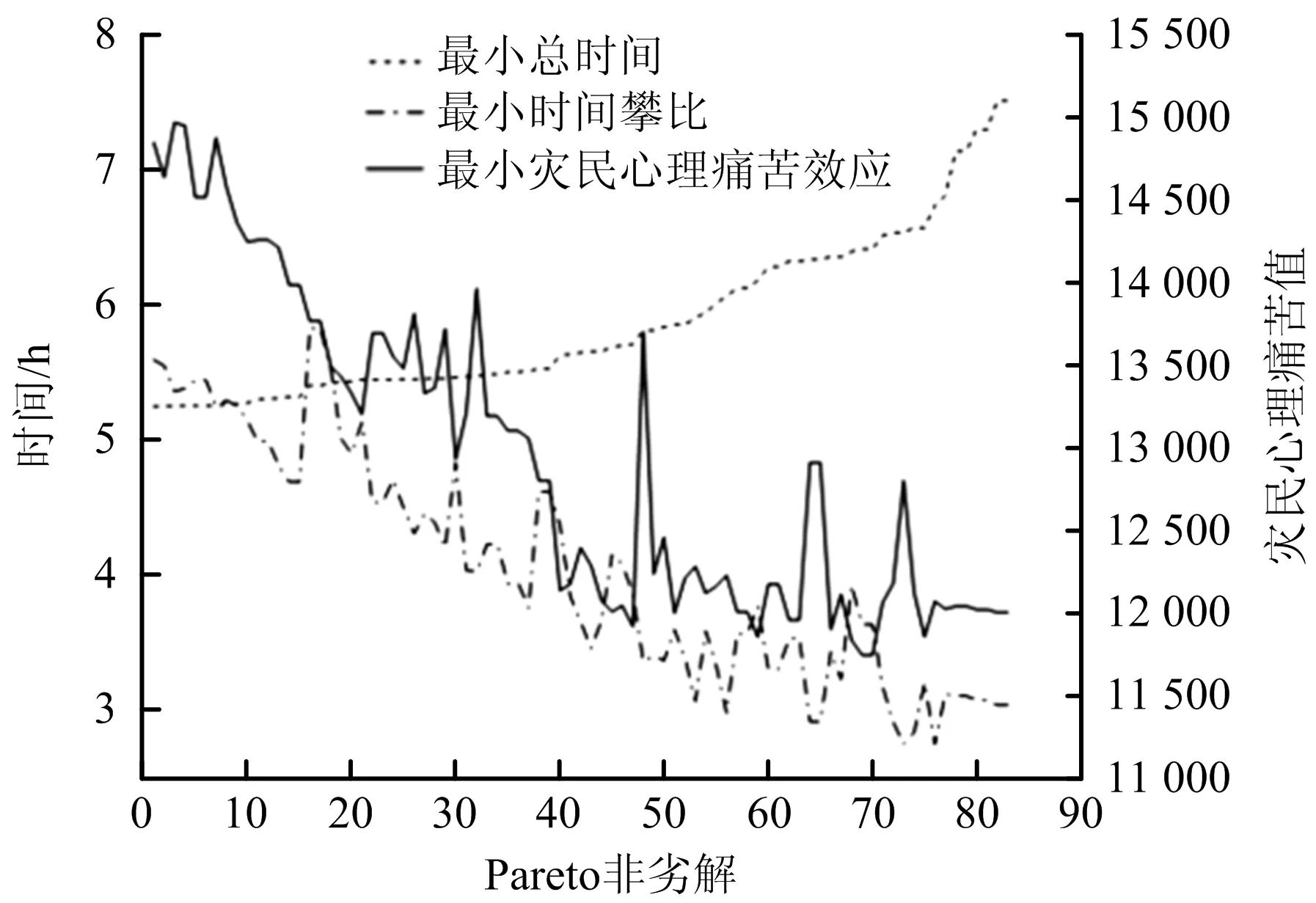
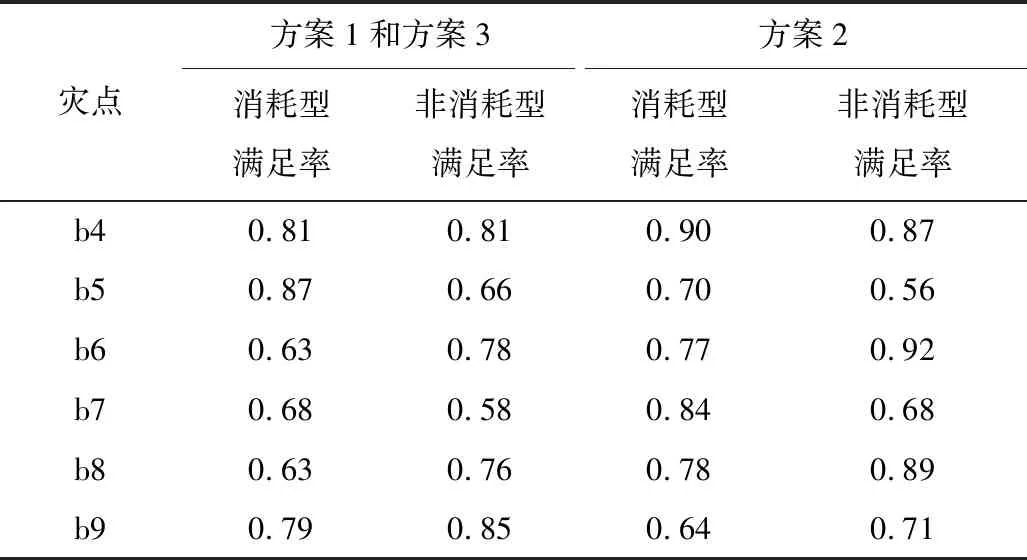
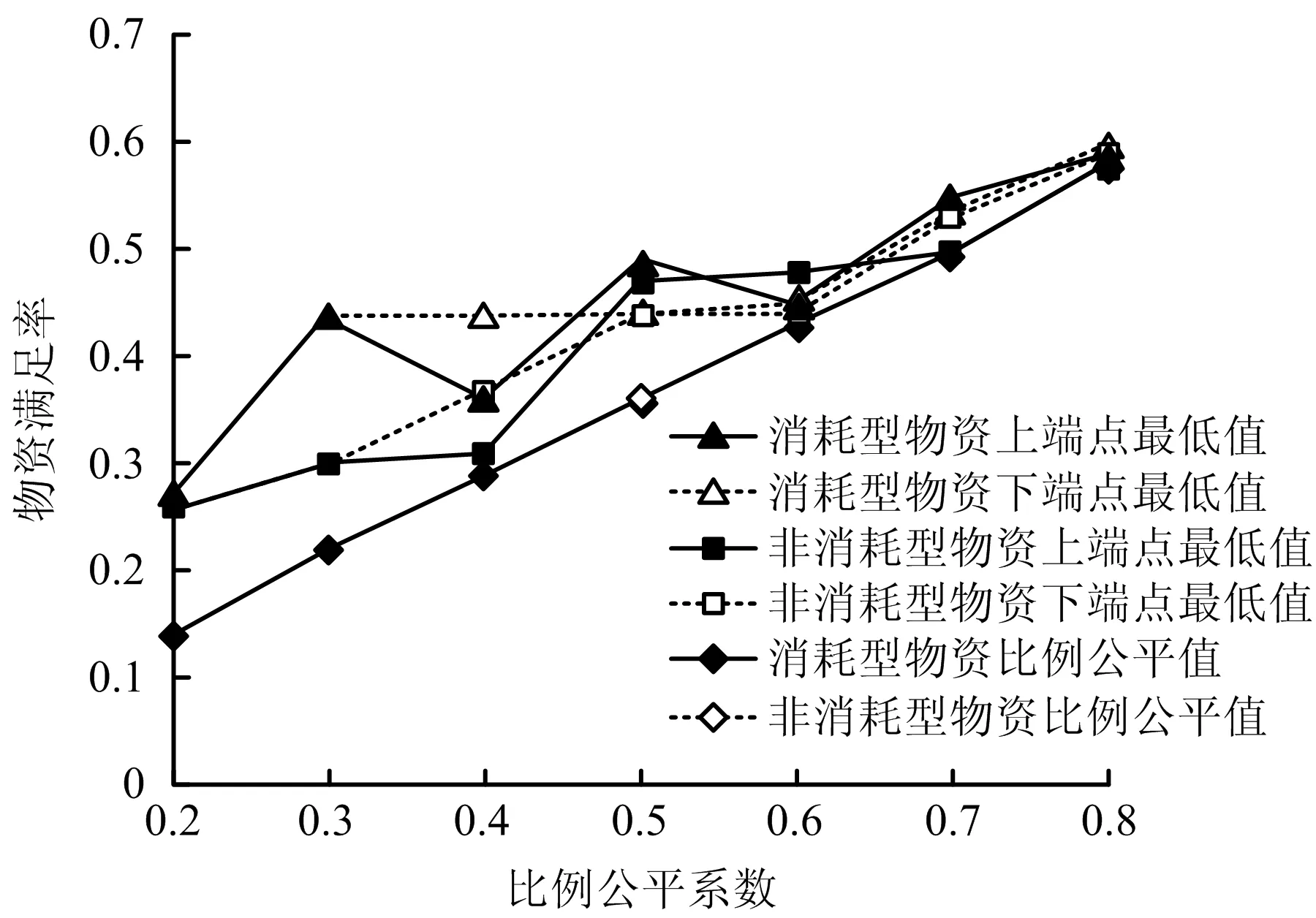
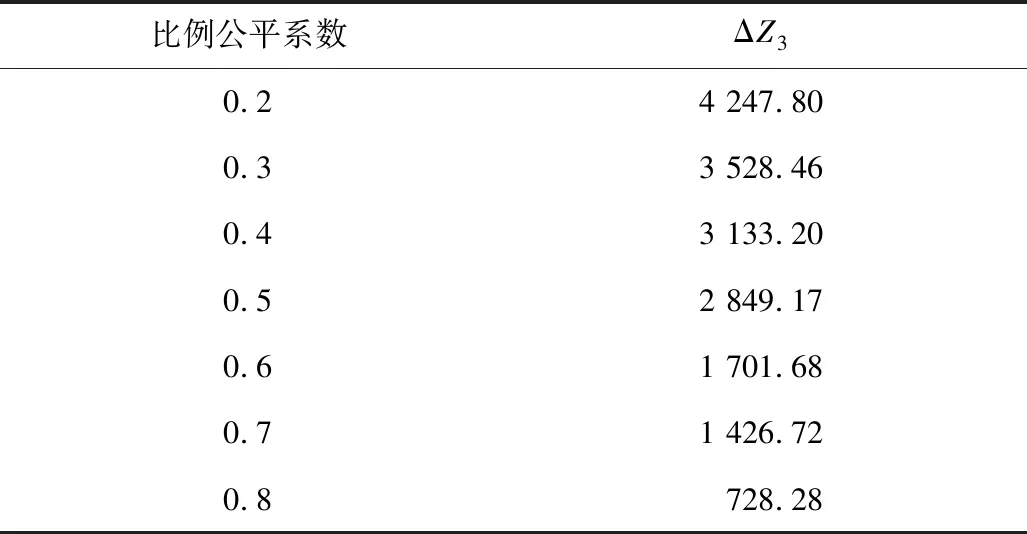
6)迭代和终止。如迭代次数gen 本文以新冠疫情期间武汉市医疗物资供给运输为背景进行仿真设计。疫情期间所需医疗物资可分为2类:消耗型物资和非消耗型物资,据调研,消耗型物资约为1 kg/套,非消耗型物资约为6 kg/套。在仿真案例中选取汉口站、国际博览中心和九州通物流仓库为配送中心,编号为a1~a3,选取武汉市16家定点医院作为医疗应急物资需求点,编号为b4~b19。以湖北省卫生健康委员会公布的2020年2月11日各医院在院治疗人数估算物资需求量,配送距离和坐标点为百度地图提取的实际距离和经纬度坐标,限于篇幅本文仅列出基础数据的部分数据,见表1。假设在常规路况下,车辆载重q=7.5 t,行驶速度v=60 km/h,设置重要度系数ρ=(0.5,0.5),比例公平系数σ=0.5;心理痛苦效应的参数设置参考文献[15],消耗型物资a1=0.846,u1=1.761,非消耗型物资a2=5.912,u2=1.814。 表1 基础数据Table 1 Basic data 采用Matlab R2016a编程,在Intel(R)Core(TM)i5-10210U CPU@ 1.60GHz2.11GHzde的计算机运行。算法参数设置为:种群规模为100,迭代次数为maxgen=600,交叉概率为0.8,变异概率为0.1。 目标函数的迭代结果分布如图2所示,3个目标值皆能迅速收敛,可得到各目标趋于稳定的最优解,验证了所建模型的有效性。 图2 目标函数的迭代结果分布Fig.2 Distribution of iterative results of objective function 基于前面参数设定,算法终止时,得到83个Pareto非劣解,非劣解筛选机制按照目标Z1排序,对非劣解中3个目标函数值进行分析,得到Pareto非劣解的收敛趋势,如图3所示。由图3可知,目标Z2和Z3的波动趋势完全相反,这是因为多目标非劣解两两互不支配。由趋势对比可知,随着目标Z1不断增大,目标Z2和目标Z3总体呈下降趋势,表明应急物流决策的绩效目标之间存在悖反关系,优化时效性的同时,必然存在公平性或心理效应的损失,反之亦然。 图3 Pareto非劣解收敛趋势Fig.3 Trend of Pareto non-inferior solution convergence 为进一步分析多目标之间的影响关系,本文选取3组分别基于3个最优目标函数下的非支配解,得到所对应的车辆路径和物资分配方案。 3个方案最优目标对比和路径规划方案见表2,在方案1中,目标函数Z1占优时,运输总时间最小为5.248 h,单辆车可为较多灾点服务,但忽略了各灾区的等待时间差异,导致灾民心理痛苦缓解程度最低。方案2中,目标函数Z2占优时,时间攀比值最小为2.747 h,对比方案1的结果,方案2的时间攀比值和灾民心理痛苦效应分别优化了51%和18.7%,服务车辆由6辆增加到10辆,出现了更多为单个灾点配送物资的车辆,虽然使调度总时间增加,但能有效缓解灾民心理痛苦。方案3中,目标函数Z3占优时,灾民心理痛苦效应最小为11 742.515,该方案能兼顾应急调配的及时性和公平性,对比方案1的结果,灾民心理痛苦效应值降低20.9%,时间公平性提高34.6%。3个方案的应急物资分配方案见表3,由于篇幅限制,仅列出部分灾点分配结果。方案1和方案3具有相同的物资分配结果,但方案3的各灾点等待时间更短,车辆路径方案不同产生差异性的物流绩效。因此,在应急响应中,提高运输资源配置能保障救援活动的高效性,本文所构建的模型较好地兼顾到资源短缺情况下应急资源调配的公平性和时效性,可以有效降低灾民心理痛苦,能得到不同目标偏好下的路径规划和应急资源分配方案,决策者可根据实际需求和决策偏好选择合适的决策方案。 表2 3个方案最优目标对比和路径规划方案Table 2 Optimal objective comparison and route planning plans of three schemes 表3 应急物资分配方案Table 3 Schemes of emergency material distribution 在其他参数不变的情况下,分别取比例公平系数σ=0.2~0.8,计算各目标函数Pareto前沿的端点解。2类应急物资在不同比例公平程度下端点解最低需求满足率如图4所示,随着σ的增大,物资分配数量的最低满足率逐步上升;说明比例公平程度越高,物资分配越公平。不同比例公平下目标Z3端点解的差值范围见表4。由表4可知,当σ=0.8时,目标函数Z3端点解的差值ΔZ3相较于σ=0.2时降低了82.9%,是因为σ的增大使模型的可行域减小,各灾点物资分配数量的差距缩小,进而使灾民心理痛苦效应的范围逐渐减小。因此设置比例公平约束能根据各灾区不同的受灾情况制定相对公平的物资分配方案,可以平衡灾民的非理性心理情绪,符合实际调度需求。 图4 不同比例公平程度下端点解的最低需求满足率Fig.4 Minimum demand satisfaction rate of endpoint solutions under different proportional fairness 表4 不同比例公平下目标Z3端点解的差值范围Table 4 Difference value range of objective Z3 endpoint solution under different proportional fairness 1)构建的多维公平测度下考虑灾民心理感知效应的应急资源调配模型,能将灾后的应急物资分配和车辆路径规划相结合,兼顾应急救援过程中的时间和供需公平,实现理论研究和现实救援场景下的同构性。 2)模型和算法能有效减少灾民心理痛苦程度,最大限度地保证救援公平性,揭示了多目标之间存在益损悖反关系,决策者可根据实际情况和经验,在Pareto非劣解集中选择不同目标偏好下的决策方案,研究结果可为政府部门制定科学高效的应急管理方案提供有效参考。 3)在构建的模型中,涉及的物资需求供给关系是静态的,考虑到灾后应急调度决策具有多阶段和连续性,研究动态情境演化的多周期应急资源调配决策模型将是未来的探索方向。4 案例分析
4.1 案例背景与参数设计
4.2 结果分析

5 结论
