应急封井装置与深水井喷喷流井口对接模拟研究*

李莹莹，任美鹏，孙晓峰，，毛 宁，谢仁军，吕 鑫，葛 阳

(1.天然气水合物国家重点实验室，北京 100028； 2.中海油研究总院有限责任公司，北京 100028； 3.东北石油大学 石油工程学院，黑龙江 大庆 163318)

0 引言

深水油气资源钻探井喷发生后，如水下井口防喷器组失效，启用应急封井装置与水下井口对接封盖井口可以迅速抑制井喷，控制井口，为后续救援提供作业时间，应急封井装置已是海上钻井服务商控制井喷失控、二次抢险的必要装备[1-2]。目前全球主流海上钻井服务商均已研制出自家配套的应急封井装置，并布置在世界各主要海洋石油开采区以备应急使用[3-6]。应急封井装置的结构性能研究方面国内学者做了大量工作，苏尚文等[7]系统介绍应急封井装置的设计结构类型；董星亮等[8]模拟3 000 m水下应急封井装置在不同原油喷速下的平衡性影响因素；李倩等[9]研究应急封井装置在水下工作状态下的磨损情况；张春雨等[10]基于材料疲劳寿命的Miner理论对应急封井装置二次封盖进行有限元静载分析得到二次封盖的危险部位；顾纯巍等[11]分析波浪等因素对应急封井装置下放缆绳作业的影响规律。目前应急封井装置的力学结构优化、耐腐蚀性以及冲蚀磨损等方面的研究较多，而应急封井装置与井口对接问题研究较少。2010年墨西哥湾深水地平线钻井平台井喷失控[12]，经历83 d救援后，最终采用应急封井装置成功封盖该井控制溢油，这是目前为止全球唯一应用案例，凸显了该类装置的应用经验不足。本文基于CFD模拟方法，研究水下喷流井口喷出的高速气体对应急封井装置下放时海域流场影响，为预测对接风险，优化装置结构性能提供指导。

1 海域对接建模和CFD数模控制方程

1.1 应急封井装置三维建模

水下应急封井装置主要包括液压连接器、水下双闸板防喷器、水管汇连接器、数据声呐监测系统等。根据调研的应急封井装置结构特点，对装置进行简化，应急封井装置简化模型如图1所示。建模中保留承受井喷流体作用力的筋板结构，以及起导向作用的通口真实形状尺寸及位置，同时将应急封井装置的主通道设置为打开状态。简化后应急封井装置的尺寸长宽高分别为：1 m0.66 m1.6 m。

图1 应急封井装置简化模型Fig.1 Simplified model of emergency well plugging device

1.2 海域流动建模和计算网格划分

以水下井口为坐标原点，由于海域具有各向同性，因此，模拟海域采用了圆柱体流域的三维网格模型如图2所示。

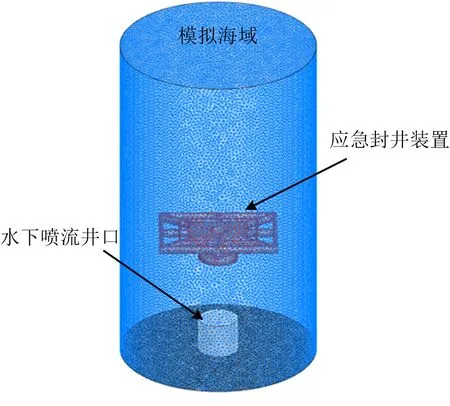
图2 模拟海域三维网格模型Fig.2 Three-dimensional grid model of simulated sea area

模拟海域底面圆直径3 m，高6 m，生成非结构网格总量1 807 903个，井口直径为0.5 m，井喷喷流为气相，海域为液相。其入口边界条件采用速度入口，出口设置为压力出口，模拟水深为1 000～3 000 m的水下环境，即将压力出口设置为10～30 MPa。

1.3 海域对接CFD模拟控制方程组

海域液相和气相的连续性方程如式(1)～(2)所示：

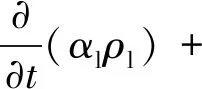
(1)

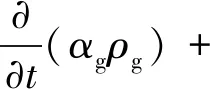
(2)

式中：t为时间，s；αg为气相体积分数；αl为液相体积分数；ug为气相速度矢量,m/s；ul为液相速度矢量，m/s；ρ为密度，kg/m3。

液相和气相的动量方程如式(3)～(4)所示：

(3)

(4)

式中：g为重力加速度，m/s2；τ为应力张量，N；p为压力，Pa；β为气液相间动量交换系数。

气相和液相之间的动量交换系数关系如式(5)所示：

(5)

式中：τp为松弛因子；f为曳力系数。

曳力系数f是由曳力系数模型[13-15]计算所得，如式(6)～(8)所示：

(6)

(7)

(8)

式中：Re为雷诺数；dg为气泡直径，m。

根据流动模拟初始条件可知，喷流井口附近流动为湍流，模拟选用标准k-ε涡流黏度模型计算因湍流脉动引起的雷诺应力耗散问题，计算域控制方程组采用有限体积法一阶迎风格式离散，离散方程应用协调一致的压力-速度耦合半隐式算法SIMPLEC[15]求解，对每个标度残差分量使用10-5的收敛准则指定2个连续迭代之间的相对误差，模拟由28台Quanta T41S-2U服务器计算，时长约30 d。

2 模拟结果分析

2.1 对接距离对喷流井口流场的影响规律

为研究应急封井装置与对接井口的距离对喷流井口流场影响，本文将模拟对接距离以1，2，3 m 3个水平展开。

对接距离对速度流场的影响如图3所示，井口喷流速度为200 m/s。随着装置与对接井口接近，应急封井装置附近气相局部速度增加，作用面迎流速度大于喷流井口流速，达到220 m/s，这是因气体喷出后压力和速度的瞬变引起的局部压缩增压和释放，说明应急封井装置越接近井口，受到的流体作用越复杂。

应急封井装置底部受力面以及附近流域压力分布如图4所示，装置由距井口3 m下放至1 m过程中，短轴方向压力增长速率高于长轴方向，短轴方向压力增长幅度约为87.5%，长轴方向压力增长幅度约为50%，压力覆盖范围逐渐由中心向流域边界扩散。

图3 对接距离对速度流场的影响Fig.3 Influence of docking distance on velocity flow field

图4 不同下放高度应急封井装置底部压力分布云图Fig.4 Cloud chart of pressure distribution at bottom of emergency well plugging device

2.2 偏距对喷流井口流场的影响规律

应急封井装置与水下喷流井口对接时可以水平对接或垂直对接，但无论哪种方法因水下作业环境的复杂性，均存在应急封井装置与井口轴线间出现偏距问题。因此，本文在喷流井口流速为200 m/s条件下，对偏距为0.5，0.25，0 m(对正)时的井喷流场开展模拟，偏距对喷流井口流场影响规律如图5所示。

偏距从0.5 m至0 m过程中，井喷羽流逐渐转变为Y型剖面，喷口流速核一部分由应急封井装置中心孔喷出，另一部分则转换为压力势能作用于装置筋板底面，形成冲击力。

图5 偏距对喷流井口速度流场的影响云图Fig.5 Cloud chart for influence of offset on velocity flow field of jet wellhead

偏距对应急封井装置所受冲击力的影响规律如图6所示，井口流体喷速为200 m/s时，装置与井口对正的过程中，所受冲击力逐渐降低，由1 250 kN减小至1 050 kN。偏距从0.5 m减小至0.25 m时，所受冲击力降低4.4%；偏距从0.25 m降至0 m时，所受冲击力降低14.4%。这表明水平方向对接时，应急封井装置进入井口喷流速度核初期所受的冲击力最大，随着向井口中心对正，冲击力降至最低。

2.3 井喷流速对喷流井口流场的影响

喷速对井口对接流场的影响规律如图7所示，模拟条件为应急封井装置距离喷流井口高度1 m，偏距0 m，喷速分别为200，300，400 m/s。由图7可知，随着喷流速度增加，井喷流体羽流发散范围更广，羽流的Y型角逐渐变成更大的钝角，并且随着喷流井口速度的增大井喷流速核随之增大，喷速为200 m/s时井喷流速核发散高度与400 m/s时相差0.25 m，这表明当应急封井装置处于相同高度时，井喷流体的喷速越小海底压力的压缩作用越明显，封井装置所受的冲击力越小。

图6 偏距对应急封井装置所受冲击力的影响规律Fig.6 Influence of offset on impact force of emergency well plugging device

图7 喷速对井口对接流场的影响云图Fig.7 Cloud chart for influence of injection velocity on velocity flow field of jet wellhead

喷速和距井口高度对冲击力的影响规律如图8所示，井喷喷速分别为200，300，400 m/s条件下，应急封井装置所受冲击力随距离井口高度的变化曲线。装置从3 m下放至距井口2 m过程中，冲击力随距井口距离降低而增大，且3种喷速条件下增大速率基本一致，均为线性增加；装置从2 m下放至距井口1 m过程中，200，300 m/s喷流井口条件的冲击力增长趋于平缓，400 m/s的喷流井口条件下的冲击力仍线性增加，说明装置下放与对接井口接近的过程中，冲击力的增长速率和喷流井口流速正相关。

图8 喷速和距井口高度对冲击力的影响规律Fig.8 Influence of injection velocity and height from wellhead on impact force

3 结论

1)应急封井装置由距井口 3 m下放至 1 m过程中，其短轴方向压力增长幅度约为87.5%，长轴方向压力增长幅度约为50%，压力覆盖范围逐渐由中心向流域边界扩散。

2)应急封井装置由距井口2 m下放至1 m过程中，喷速为200～300 m/s时，装置所受冲击力增加趋势相同，而喷速为400 m/s时冲击力增加趋势为前二者的2倍，由此可见，喷速增加对应急封井装置所受冲击力的影响较大。