室内人员疏散时间快速预测模型研究*
2021-05-12江延立盖文妹
江延立,盖文妹,李 群
(1.中国地质大学(北京) 工程技术学院,北京 100083; 2.中国安全生产科学研究院,北京 100012)
0 引言
人员必需疏散时间由3部分构成:探测报警时间、人员预动作时间和人员疏散时间。其中,人员疏散时间是决定人员能否安全疏散的主要因素[1]。人员疏散时间计算方法包括仿真模拟法和经验公式法[2]:仿真模拟法基于数学模型与计算机技术,直观展示人员疏散过程,当假设条件和参数与实际相符时,能够得到比较准确的人员疏散时间,常见仿真模拟软件包括Pathfinder、Legion和Anylogic等,仿真模拟法基础模型为社会力模型、势能场模型等数学模型[3-4],普遍存在参数标定难、计算复杂等问题,实用性较差;经验公式法一般由数学模型简化而来,且大部分公式为经验公式[5-12]。与仿真模拟法相比,经验公式法精确度较低,但因其高效性和节约计算资源等优点,被广泛应用于工程实践。通过简化复杂数学模型,建立精确、高效计算方法,工程实践意义重大,是宏观模型发展重要方向。
日本学者Togawa以“进出”人员数量为临界条件,建立适合单出口多通道的Togawa行人疏散模型,由于没有合适方法计算人员出口处滞留时间,导致Togawa行人疏散模型计算量庞大,实用性较低。部分学者针对Togawa行人疏散模型缺陷,提出不同改进思路:潘应久等[13]通过分析传统Togawa模型推导过程,在行人疏散动态交通特性分析基础上,基于迭代思想和离散计算方法对传统Togawa模型进行改进,建立看台区行人疏散时间模型;张青松等[14]基于人群流动理论和离散计算方法,对传统Togawa疏散时间计算公式进行改进,并提出疏散离散时间计算模型(EDTM),与计算机模拟结果比较接近,并且比传统Togawa疏散时间计算公式更为精确;郑丹等[15]针对传统疏散模型疏散时间参数不确定问题,采用离散算法和Fruin模型,对传统Togawa疏散模型进行改进,将时间离散为多个微小单元,假设各时间单元内人流密度不变,通过Fruin模型确定Togawa模型参数值,并运用迭代法得到疏散时间,提高计算精确度。
上述改进方法均通过改进算法层面优化传统Togawa模型,计算逻辑与实用性没有得到很好提升。本文基于传统Togawa模型,将疏散过程分为出口非线性疏散阶段和出口线性疏散阶段,采用逐步扩大计算区域方法,建立基于人员流动速率的疏散时间快速预测模型,并利用Pathfinder软件进行仿真验证。
1 室内人员疏散时间快速预测模型
1.1 判断临界条件
线性与非线性疏散阶段划分依据为2种疏散状态临界条件。疏散初期,出口处比较通畅,出口附近人员迅速向出口靠拢,极易造成小范围堵塞,与锥形瓶实验相似,如图1所示。
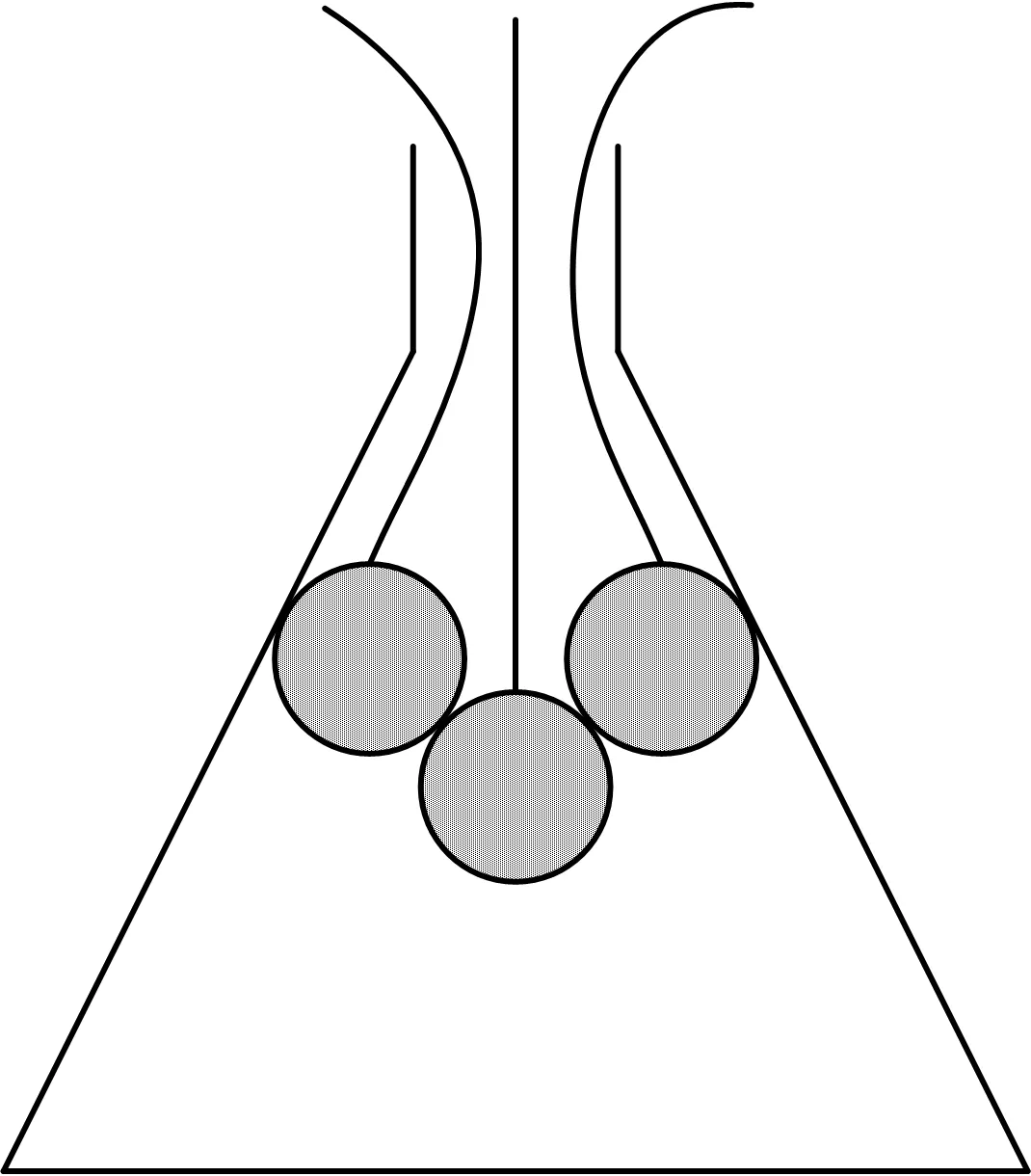
图1 锥形瓶实验Fig.1 Experiment of conical flask
紧急情况下,房间内所有人员均以最快速度向安全出口疏散,当同时抵达出口人员数量大于该出口单位时间最大疏散人员数量时,将形成小范围堵塞,后续人员迅速赶到,使出口处出现滞留现象。此时,因人员冲撞,在出口处形成不规则且连续的弧形堵塞,即形成僵持局面。人员滞留表征线性疏散阶段开始,出口将以最大流动系数疏散建筑内人员,线性疏散示意图如图2所示。
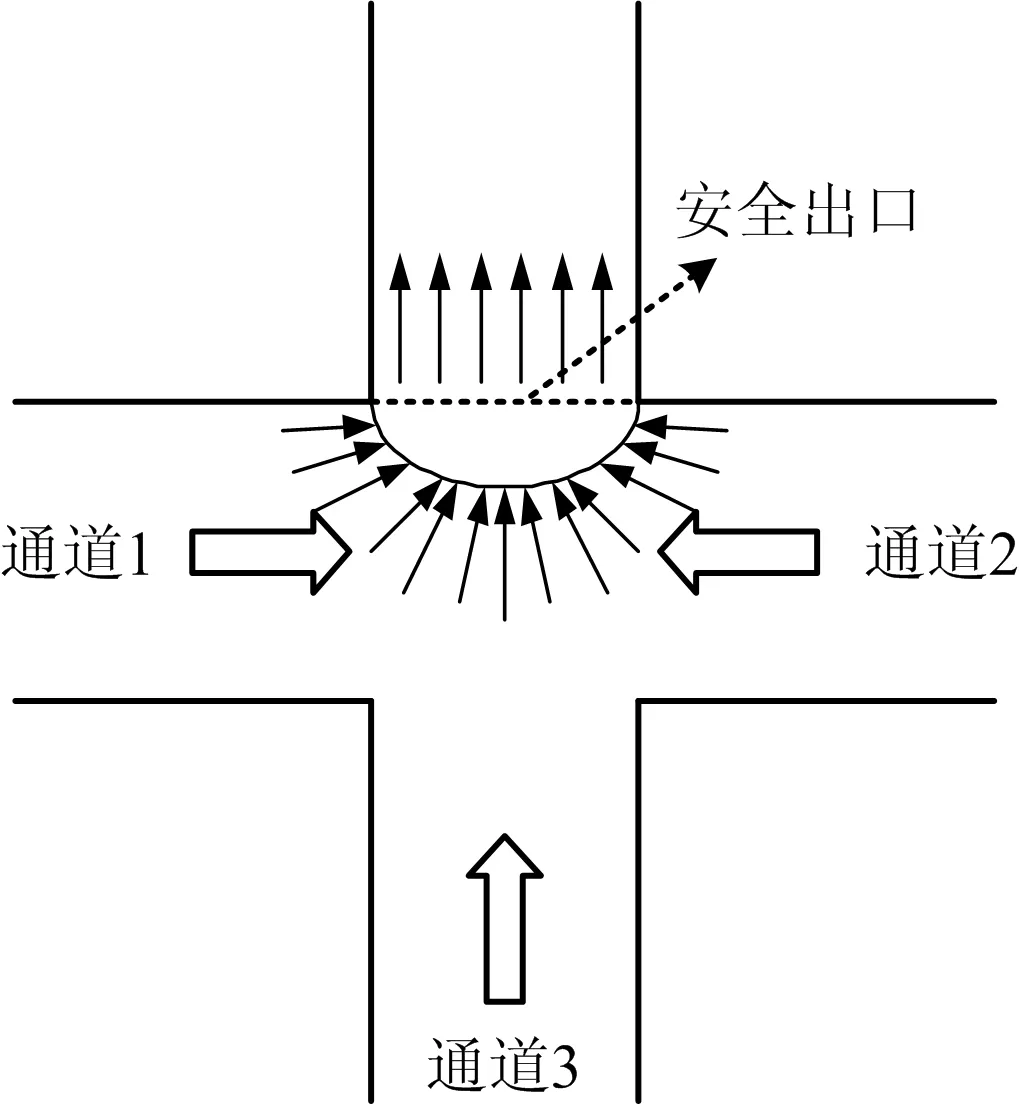
图2 线性疏散示意Fig.2 Schematic diagram of linear evacuation stage
当疏散人员进入出口流动速率wi等于出口最大人员流动速率wo时,认为出口处即将发生人员滞留,出口疏散阶段临界条件如式(1)所示:
wi=wo
(1)
式中:wi为疏散人员进入出口流动速率,人/s;wo为出口最大人员流动速率,人/s。
1.2 各阶段时长
采用逐步扩大计算域方法,计算人员流动速率,当达到临界条件时结束计算。室内人员疏散时间快速预测模型计算逻辑如图3所示。由图3可知,逻辑图包括以下2个步骤:
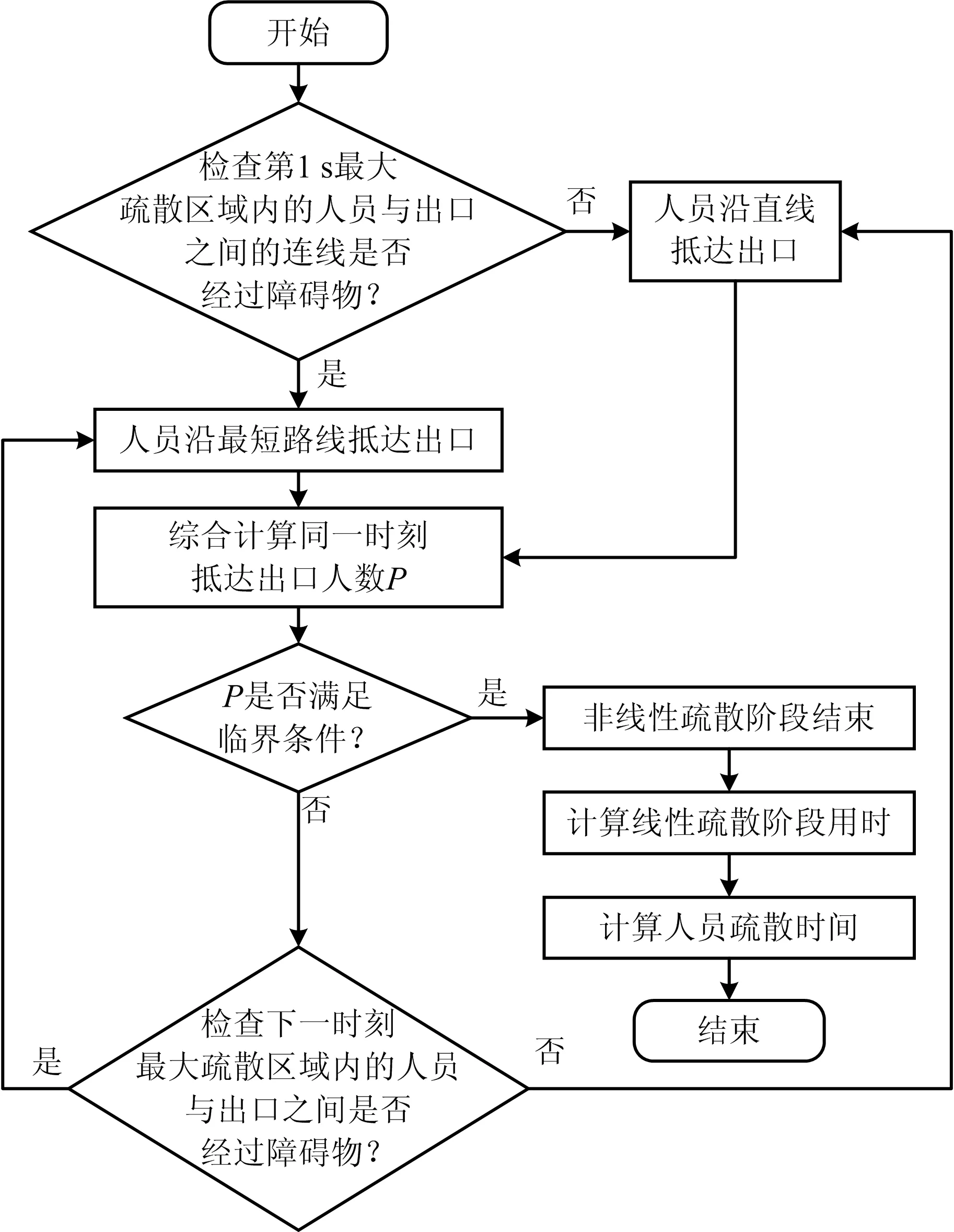
图3 快速预测模型计算逻辑Fig.3 Calculation logic of rapid prediction model
1)由出口附近开始,检查第1 s最大疏散区域内人员与疏散出口处连线是否经过障碍物,若不经过障碍物,人员沿直线抵达出口,反之则沿最短路线疏散。快速预测模型示意图如图4所示。
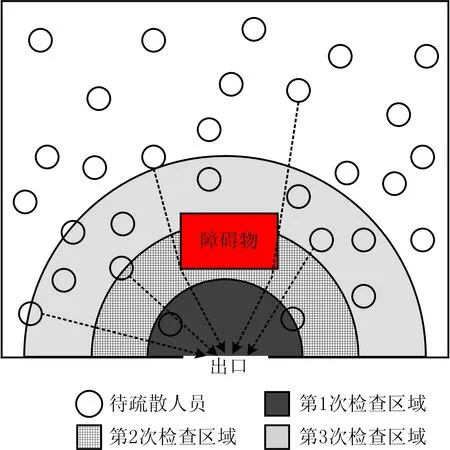
图4 快速预测模型运行示意Fig.4 Schematic diagram for operation of rapid prediction model
2点间最短距离求解主要遵循以下原则[16]:2点之间直线距离最短;2点间有直边障碍物(如栏杆或矩形障碍物)时,最短路线必通过直边障碍物端点;2点间有曲边障碍物(如大厅立柱等)时,最短路线必与曲边障碍物相切,并沿障碍物边缘延伸一段距离;当同一场景下同时存在多条满足上述原则路线时,选取最短路线进行计算。
疏散时间t应将人员转向时间考虑在内,如式(2)所示:
(2)
式中:t为单个人员疏散时间,当t∈(m,m+1]时,记t=m+1,m=0,1,2,…,s;n为行人转向次数,n=0,1,2,…;t′为行人每次转向所需时间,s;t″为人员运动时间,s;L为行人疏散路线长度,m;v为行人运动速度,m/s。
由于人的决策受多种因素影响,疏散人员可依据其认为最优路线进行疏散。最优路线可通过社会力模型、势能场模型等连续微观模型确定,但会增加计算量,不利于工程实践。
2)检查该时刻抵达出口人员数量P是否达到临界条件,若未达到临界条件,检查下一时刻最大疏散区域内人员与出口之间是否有障碍物,重复该步骤,直至满足临界条件;若达到临界条件,标记该时刻T1,非线性疏散阶段结束,设此时疏散人员数量P1。
计算线性疏散阶段时长T2,根据线性疏散阶段特征,T2为房间内剩余人员数量P2与出口最大人流率w0的比值,如式(3)所示:
(3)
1.3 快速预测模型与传统Togawa模型计算效率对比
从计算逻辑角度对比快速预测模型与传统Togawa模型计算效率。Togawa模型需根据人流和疏散环境划分通道,表征出口滞留时刻T0前,分通道人员流动速率fi与时间t函数关系;将所有通道人员流动速率fi分别对时间t积分,得到出口发生滞留前疏散人员数量;最后计算过程与快速预测模型类似。计算公式如式(4)所示:
(4)
式中:T为人员疏散时间,s;n为通往安全出口分通道数量,分通道可能是物理存在,也可能由于障碍物分流作用形成;f表示安全出口最大人员流动速率,人/s;fi为第i条通道人员流动速率,人/s;P为待疏散人员数量;T0为人员滞留时刻,s。
由于式(4)存在多个不确定因子,一般采用经验公式法[17]。传统Togawa模型计算方法因计算量庞大,在实际工程中应用较少。
快速预测模型进一步简化人员疏散过程,不考虑各分通道具体人员流动,只考虑出口处人员进出过程,并提出出口滞留临界条件及逐步扩大计算区域法。逐步扩大计算区域法非全局计算,且非线性阶段较短暂,相对Togawa模型计算量大幅下降,更适用于工程实践。
2 快速预测模型应用及对比分析
2.1 快速预测模型应用
以某房间人员疏散为研究对象,房间内部随机分布60位行人,房间结构及人员分布如图5所示。设房间出口宽度2 m,由SFPE手册[18]可知,出口最大人流率wo=2.6人/s,行人运动速度v=1.2 m/s,行人转向时间t1=0.3 s。
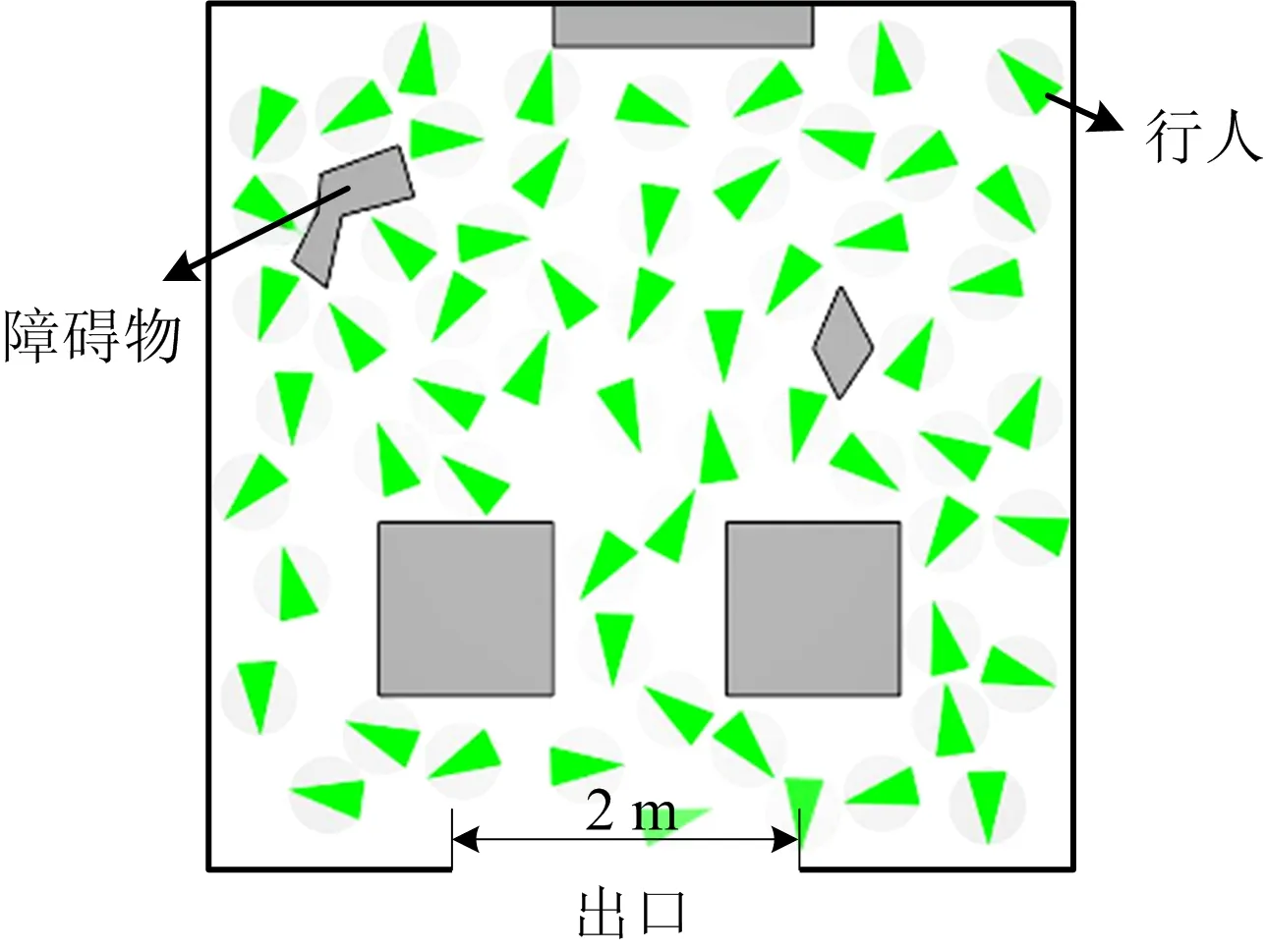
图5 房间结构及人员分布Fig.5 Room structure and personnel distribution
疏散开始后第1,2 s最大疏散区域如图6所示。由图6可知,疏散区域由1个矩形和2个扇形构成,矩形横边为安全出口宽度,第1,2 s人员最大运动距离分别为1.2,2.4 m;2个扇形分别以安全出口左右顶点为圆心,以人员每时刻最大运动距离为半径的圆的一部分。在第1 s最大疏散区域内共有11位行人没有被障碍物阻挡。
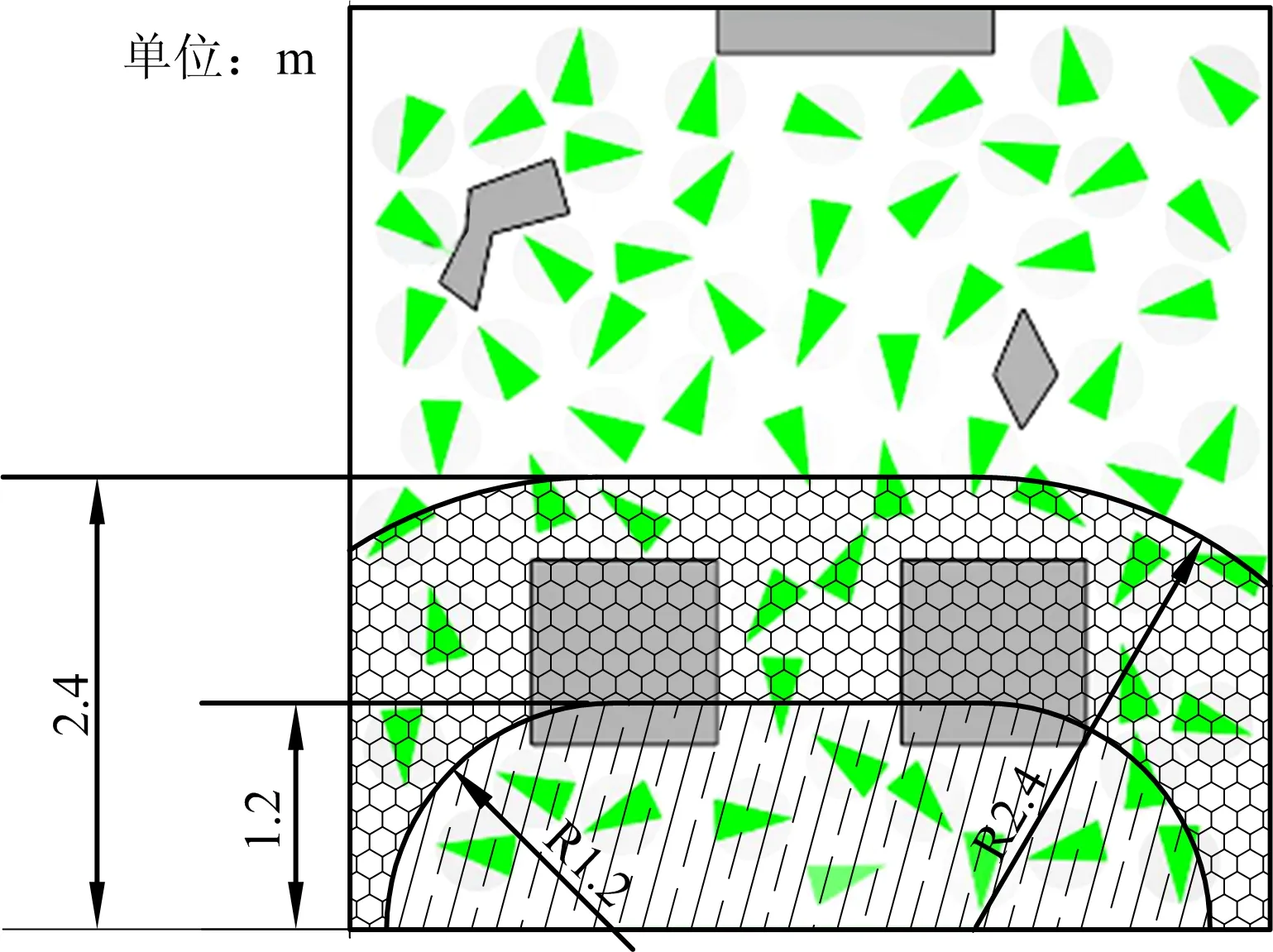
图6 第1 s和第2 s最大疏散区域示意Fig.6 Schematic diagram of maximum evacuation area 1st and 2nd seconds
根据式(2)计算疏散时间,其中部分行人疏散时间见表1。
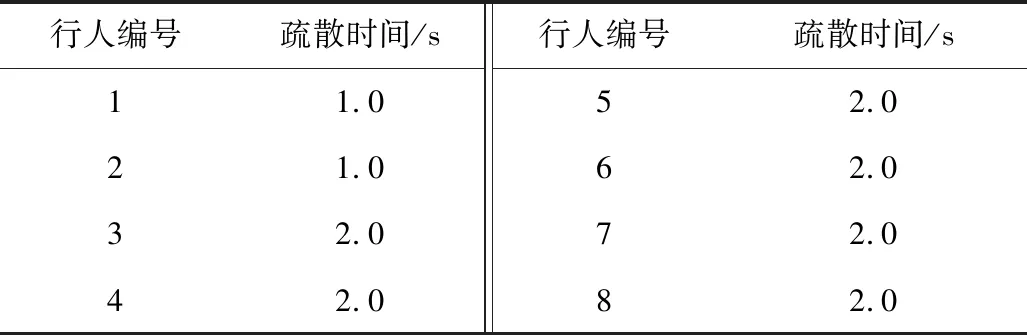
表1 部分行人疏散时间Table 1 Evacuation time of partial pedestrian
由表1可知,第1 s人员到达出口速率为2人/s,小于wo,因此不满足临界条件;第2 s人员到达出口速率至少为6人/s,大于wo,满足临界条件,非线性阶段结束,出口处出现滞留,即T1=2 s,P1=2人。根据式(3)得到线性阶段时长T2≈22.3 s,则人员疏散总时间T≈24.3 s
2.2 对比分析
Togawa经验公式如式(5)所示:
(5)
式中:T为人员疏散时间,s;P为待疏散人员数量;wo为出口最大人员流动速率,人/s;L′为步行最大距离,m;vl为人员移动速度,m/s。
设L′为距离出口最远处人员疏散路线长度,L′≈8 m。则根据式(5)计算人员疏散时间T=29.7 s。
Pathfinder仿真模拟软件一般用于建筑内人员疏散,操作方法简单,仿真结果直观可见,拥有多个可变参数,可适用于不同疏散情况。在Pathfinder软件中建立人员疏散模型,得到出口人流率变化曲线如图7所示。
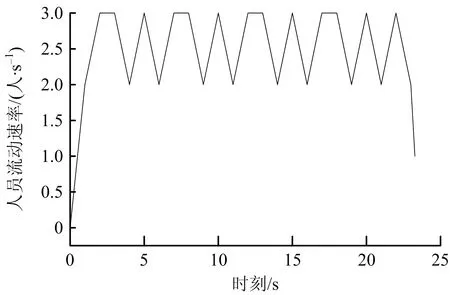
图7 出口人流率变化Fig.7 Change curve of personnel flow rate at exit
由图7可知,人员疏散时间T≈23.3 s,非线性阶段T1=2 s,非线性阶段疏散人数P1=2人。
对Pathifinder仿真结果、快速预测模型计算结果与Togawa经验公式计算结果进行汇总,见表2。
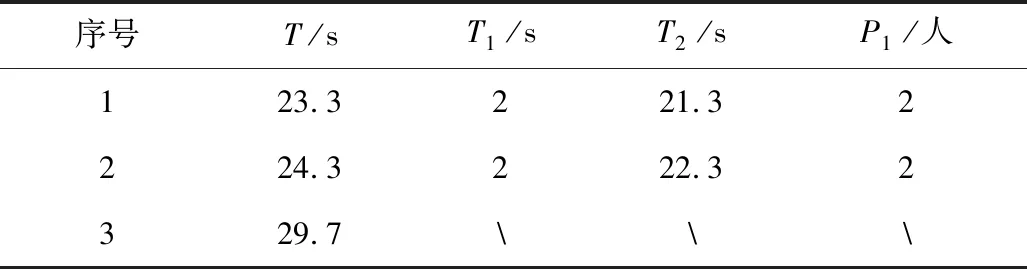
表2 计算结果汇总Table 2 Summary of calculation results
由表2可知,相比Togawa经验公式法,快速预测模型计算结果更加精确,同时还能得到人员滞留时刻、非线性阶段疏散人数等参数,反映一定疏散细节。
3 结论
1)通过简化传统Togawa模型,将人员疏散过程划分为2个阶段:出口非线性疏散阶段和出口线性疏散阶段;基于2个阶段间临界条件和逐步扩大计算区域法,提出室内人员疏散时间快速预测模型。
2)相较于传统Togawa经验公式法,利用快速预测模型可以获取精确人员疏散时间,得到反映疏散细节的数据信息,如人员滞留时刻、非线性疏散阶段人员数量等。
3)该模型具有一定局限性,对人员分布稀疏或极不均匀的房间,模型误差可能较大。
