饱和层状尾砂动力特性研究*
2021-05-12陈志斌王光进周汉民王星元韩亚兵康富淇
陈志斌,王光进,,周汉民,王星元,张 超,韩亚兵,康富淇
(1.昆明理工大学 国土资源工程学院,云南 昆明 650093;2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,湖北 武汉 430071;3.矿冶科技集团有限公司,北京 100160; 4.中国地质大学(北京) 土地科学技术学院,北京 100083)
0 引言
尾砂指矿厂在特定经济技术条件下,将矿石磨细,选取有用成分后排放的废弃物;尾矿库指储存废弃尾砂或其他废弃工业原料的高势能建筑物,存在溃坝、泄漏等潜在威胁[1]。地震灾害将引起尾砂液化,导致尾矿库溃坝及漫顶,威胁周边居民安全。因此,需要对高地震烈度区尾矿库建设及扩容进行严格动力稳定性研究[2]。因尾矿库稳定性很大程度取决于库内尾砂动强度特性,所以对尾砂动力特性研究意义重大。
Pradhan[3]认为黏性土夹层对砂土层抗液化强度影响较小;周健等[4]利用GDS动三轴仪器对不同厚度粉土层状试样进行试验发现,夹层对液化特性有较大影响;Ozener等[5]利用振动台研究粉土类夹层与砂土类尾砂液化关系,发现夹层对液化影响较大;Takch等[6]通过研究不同百分比粉土和砂土强度特性,得出循环剪应力比与动孔隙水压力比联系;Amini等[7]采用不同装样分层方式,研究饱和分层砂土动力特性,得出层状结构对抗液化性影响较小的结论;Yoshimine等[8]采用不同粒径分层砂土进行试验,表明层状结构砂土抗液化强度远大于单一结构砂土;修占国等[9]利用动三轴仪器研究层状砂土液化特性,发现粉状砂土层对超孔隙水压力阻碍作用大于细粒状砂土层;谭凡等[10]利用动三轴试验研究尾粉土在不同固结应力及固结应力比下动力特性,发现等压固结时饱和尾砂全部液化,偏压固结时饱和尾砂未发生液化;张超等[11]研究不同围压下尾砂动剪应力比,发现围压越高尾砂动剪应力比越小;余湘娟等[12]通过动三轴试验得到不同固结比与不同固结应力条件下尾砂动强度、动孔压与破坏振次之间拟合关系;褚卫瑞[13]通过动三轴试验研究细粒含量对尾矿砂动力特性影响,表明随细粒增多,尾矿砂动剪应力比在振次一定时,先上升后下降;李治朋等[14]研究细粒含量对粉土强度影响,得到随细粒含量增多,循环剪应力比CSR越小。
目前针对尾砂研究主要集中于单一尾砂动力试验研究,而尾砂分层现象与单一尾砂力学特性存在较大差别,因此,本文重点针对高地震烈度区尾矿库典型尾砂不同分层情况、不同固结应力下液化现象及动孔隙水增长规律进行研究,为高烈度地震区尾矿坝地震液化提供理论参考。
1 试验仪器、试验方法及试样参数
1.1 试验仪器及试验方法
试验选用KTL-DYN10型双向动三轴设备,硬件系统包括轴向加载设备、动态围压控制室、反压控制器、8通道高速控制及采集设备;软件系统为DSP高速数字控制系统,运行频率10 kHz;KTL-DYN10型双向动三轴动态加载系统动态力最大幅值±10 kN。试验开始,由计算机自动采集并记录动孔隙水压力、动应变、动应力及偏应力等参数,试验数据整理根据《土工试验方法标准》[15]。试样取自现场原尾砂筛分后的尾细砂和尾粉土,制样直径50 mm,高度105 mm。试验采用干装样法,尾砂装样如图1所示。装样结束进行饱和以提高试样饱和度,包括CO2饱和,水头饱、反压饱。饱和结束后,检测孔隙水压力系数B,当B值>0.95,视为饱和完成。饱和完成后进行固结,固结应力分别为200,400,800,1 200 kPa,固结比Kc=1.0,当1 h内固结排水量≤0.1 cm3,固结完成。最后,施加一定幅值循环荷载,直至试样破坏,振动频率1 Hz,振动波形为正弦波。以动应变幅值达到5 %或动孔压增长达到围压为试样破坏标准,应变反向时选取双幅应变,单向应变时选取塑性应变与弹性应变之和。试验方案包括以下2种:1)固结应力分别为200,400,800,1 200 kPa,尾粉土在下厚度20 mm;2)固结应力为1 200 kPa时,尾粉土在下厚度分别为0,20,40,80 mm。尾砂动力加载及试样结构破坏如图1~2所示。

图1 动力加载Fig.1 Schematic diagram of dynamic loading

图2 试样结构破坏Fig.2 Schematic diagram of sample structure failure
1.2 试样参数数据
试验用尾细砂与尾粉土筛选自现场原尾矿,试样颗粒级配图如图3所示。基于《土工试验方法标准》[15]计算试样级配,尾细砂不均匀系数Cu=12.5,曲率系数Cc=2.88,属级配良好尾砂;尾粉土不均匀系数Cu=2.29,属级配不良尾砂。
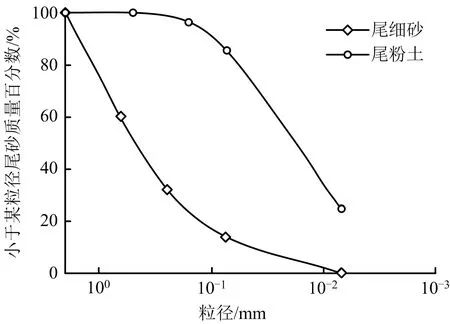
图3 颗粒级配图Fig.3 Diagram of particle gradation
2 试验结果及分析
2.1 应力应变关系分析
尾矿应力-应变关系是尾矿动力特性基本要素,动力作用下土体产生滞后特性、非线性及形变累加特性。将土体动应力-应变模型视为黏弹性模型与黏塑性模型,常用动本构模型为B.O.Hardin和V.P.Drnevich等效黏弹性模型[16-17],将尾矿颗粒视为黏弹性介质,用σed与σcd分别表示弹性动应力与黏性动应力,如式(1)~(3)所示:
(1)
(2)
或
(3)
求解微分方程,如式(4)所示:
(4)
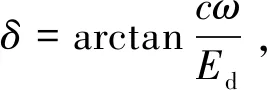
(5)
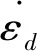
由式(5)可知,动应力最大值与动应变最大值相位不同,阻尼作用使动弹性模量大于黏弹性介质动弹性模量,当砂土黏滞系数c较小时,砂土应力和应变幅度较小;当动应力与动应变极值同时出现,精度值最高。
将尾砂土等同黏弹性物质,利用量化动弹性模量与阻尼比表示尾砂应力-应变关系非线性与滞后性关系,如式(6)~(8)所示:
(6)
λ=λmax(1-Ed/E0)
(7)
E0=kPa(σV′/Pa)n
(8)
式中:λ为阻尼比;E0为初始动弹性模量,MPa;εk为参考动应变;λmax为最大阻尼比;n为模量指数;k为模量系数;Pa为大气压力,Pa;σV′为竖向有效应力,kPa。
2.2 动弹性模量及动弹性模量倒数
尾砂动弹性模量是动应力与动应变关系关键指标,如式(9)所示:
(9)
土体动弹性模量如式(10)所示:
(10)
方案1、2动弹性模量及其倒数与动应变关系如图4~7所示。由图4可知,当尾粉土厚度为定值,随固结应力增大,试样动弹性模量增大,当εd<1×10-5时,随动应变增大,动弹性模量较平缓;当εd>1×10-5时,动弹性模量迅速下降;当εd为1×10-2时,动弹性模量趋于0,动弹性模量减小速率整体先增大后减小。层状尾砂受固结应力影响明显,固结应力越大,动弹性模量越大。动弹性模量倒数与动应变之间线性关系,直观体现不同条件下动弹性模量间变化趋势。由图5可知,随固结应力增大,直线斜率逐渐减小,且降幅较大,层状尾砂动力特性受固结应力变化影响较明显。由图6可知,在高固结应力下,随尾粉土厚度增大,εd=1×10-5依旧为动弹性模量变化拐点,最终在εd=1×10-1处趋近于0。随尾粉土厚度增加,动弹性模量降幅减小,这是因为随尾粉土含量增加,振动破坏时尾粉土产生的结构强度逐渐显现出来,试样力学特性以尾粉土为主。由图7可知,在高固结应力下,随尾粉土厚度增加,试样动弹性模量倒数与动应变关系曲线斜率逐渐增大。
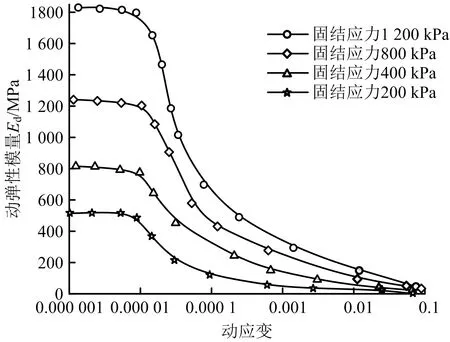
图4 方案1动弹性模量-动应变关系Fig.4 Relationship between dynamic elastic modulus and dynamic strain in scheme 1
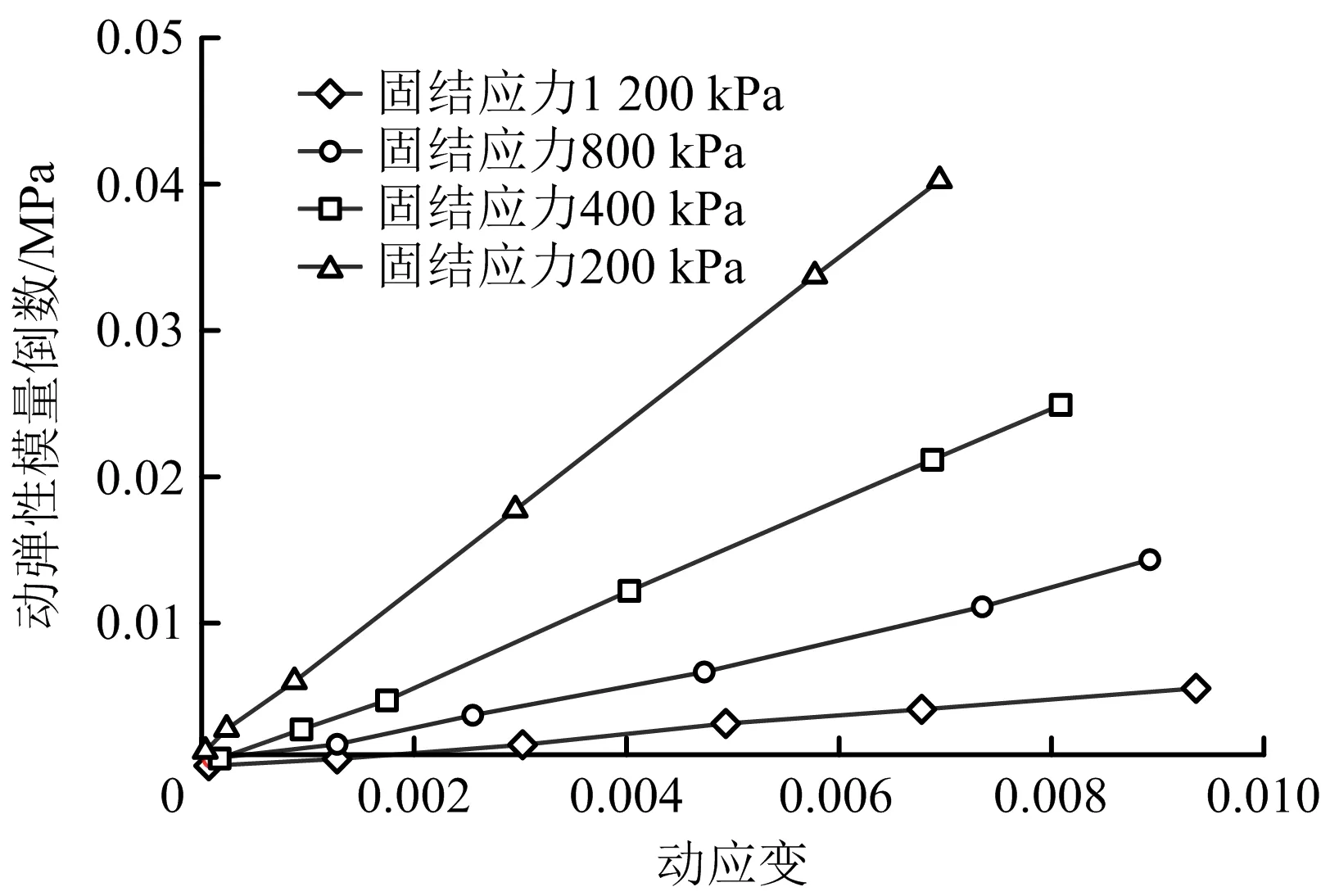
图5 方案1动弹性模量倒数-动应变关系Fig.5 Relationship between reciprocal dynamic elastic modulus and dynamic strain in scheme 1
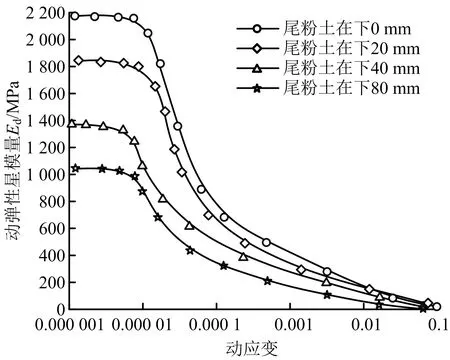
图6 方案2动弹性模量-动应变关系Fig.6 Relationship between dynamic elastic modulus and dynamic strain in scheme 2
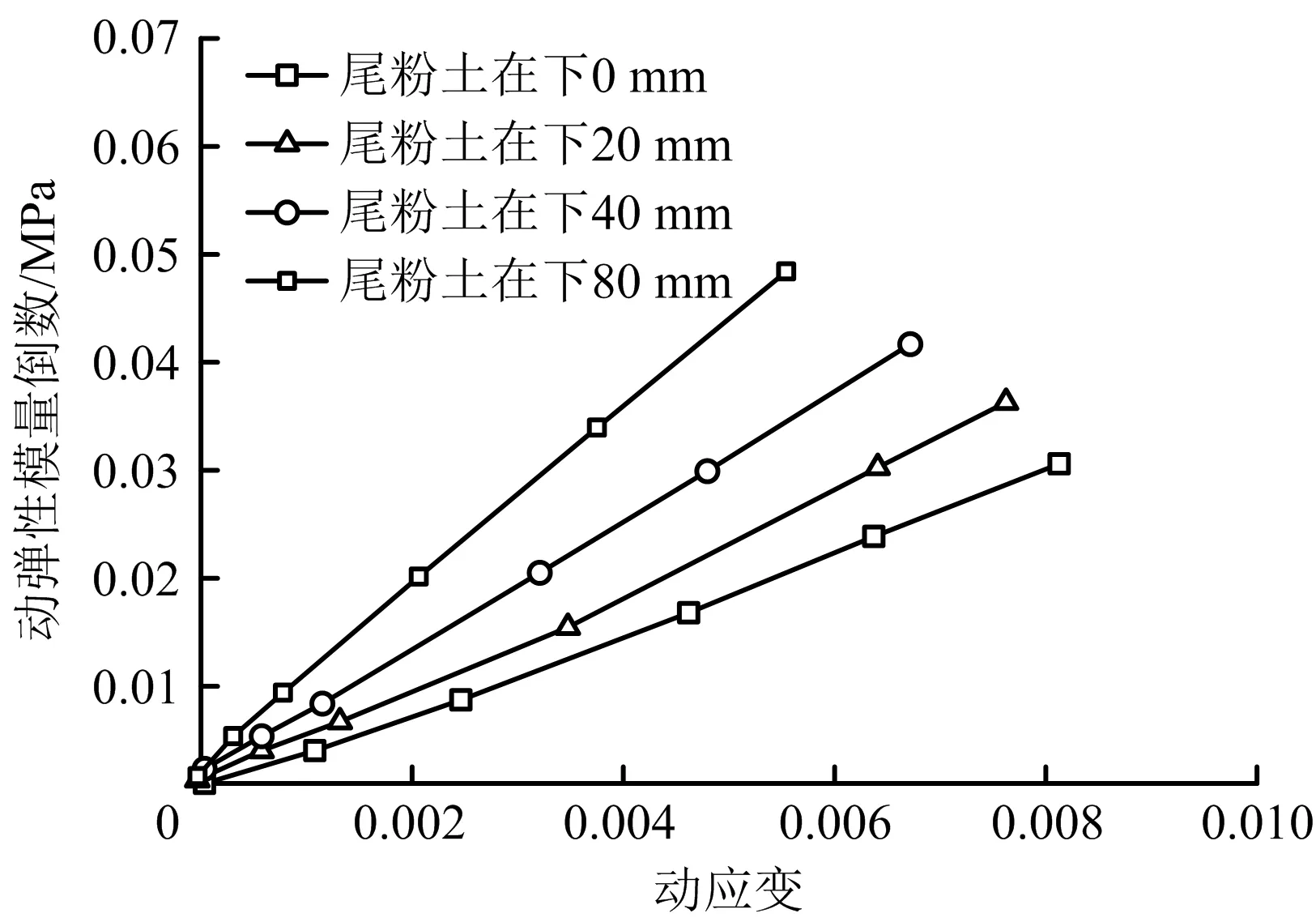
图7 方案2动弹性模量倒数-动应变关系Fig.7 Relationship between reciprocal dynamic elastic modulus and dynamic strain in scheme 2
2.3 动剪应力比、动剪切模量比及阻尼比
利用高振幅低振次应力或低振幅高振次应力,使尾砂散体颗粒在一定动荷载作用下产生剪切破坏。本文采用高振幅低振次应力加载方式。
动强度由应力比与破坏循环振次Nf关系曲线表示。某破坏振次条件下,试样45°面破坏动剪应力比τd/σ0′如式(11)~(13)所示:
(11)
(12)
(13)
式中:τd/σ0′为试样45°面动剪应力比;σd为试样轴向动应力,kPa;τd为试样45°面的动剪应力,kPa;σ0′为试样45°面有效法向固结应力σd,kPa;σ1c′为有效轴向固结应力,kPa;σ3c′为有效侧向固结应力,kPa。
谢定义[18]提出动剪切模量比与动应变幅值、阻尼比与动应变幅值关系曲线,当动应力较大时,曲线具有离散性;动剪切模量比与动应变关系曲线,即Hardin-Drnevich双曲线模型,适用于尾粉砂与尾粉土应变较小情况,如式(14)所示:
G/Gmax=1/(1+γ/γm)
(14)
阻尼比与动剪切模量比如式(15)所示:
λ=λmax=(1-G/Gmax)
(15)
式中:G、Gmax分别为动剪切模量及最大动剪切模量,MPa;γ为动剪应变;γm为参考剪应变;λ为阻尼比;λmax为最大阻尼比。
破坏振次N=8,12,20,30对应地震震级6.5,7.0,7.5,8.0。本文取地震震级8级,破坏振次30,不同试验方案下试样动剪应力比,见表1。

表1 N=30时不同试验方案下试样动剪应力比Table 1 Dynamic shear stress ratio of test samples under different test schemes when N=30
由图8~10可知,层状尾砂动剪应力比与破坏振次呈良好幂函数关系。方案1动剪应力比与破坏振次关系如图8所示,由图8可知,层状尾砂动剪应力比随固结应力增大而减小,这是因为随固结应力增大,试样由超固结状态变为正常固结状态,动剪应力比下降,最终呈现归一趋势。方案1动剪切模量比、阻尼比与动应变关系如图9所示,由图9可知,当动应变较小时,试样整体处于弹性阶段,不同固结应力下动剪切模量比与阻尼比关系曲线变化不明显;当动应变大于一定值时,不同固结应力下动剪切模量比呈下降趋势,但固结应力越大,动剪切模量比越大;试样阻尼比在相同动应变幅值下,随固结应力增大而减小。方案2动剪应力比与破坏振次关系如图10所示,由图10可知,在高固结应力下,随尾粉土厚度增加,层状结构尾砂动剪应力比先上升后下降。方案2动剪切模量比、阻尼比与动应变关系如图11所示,由图11可知,层状尾砂动剪切模量比,随动应变增大呈下降趋势,在相同动应变幅值下,尾粉土厚度越大,动剪切模量比越大;阻尼比变化趋势与动剪切模量比相反,随动应变增加,阻尼比呈上升趋势,在相同动应变幅值下,尾粉土厚度越大,阻尼比越小。
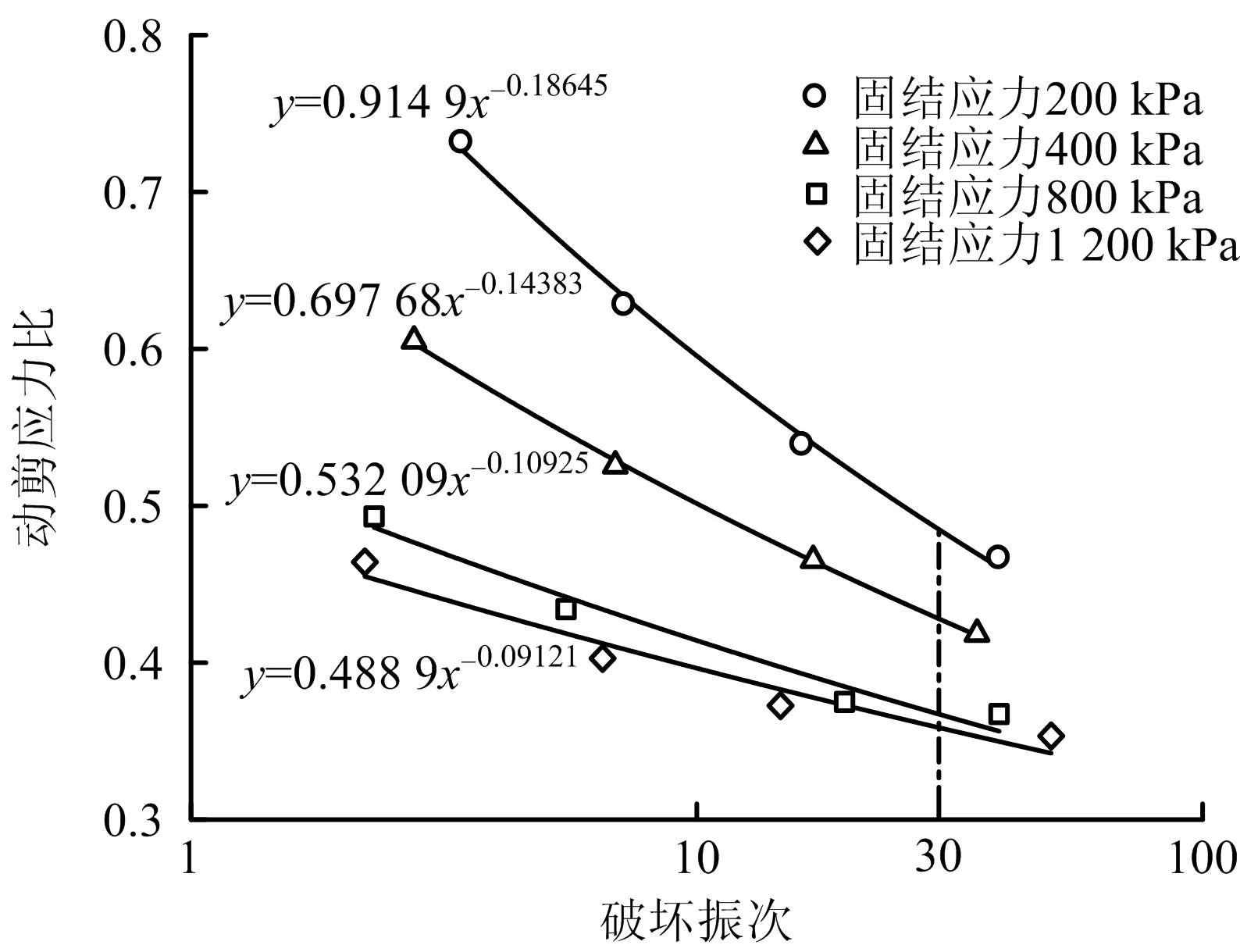
图8 方案1动剪应力比与破坏振次关系Fig.8 Relationship between dynamic shear stress ratio and failure vibration times in scheme 1
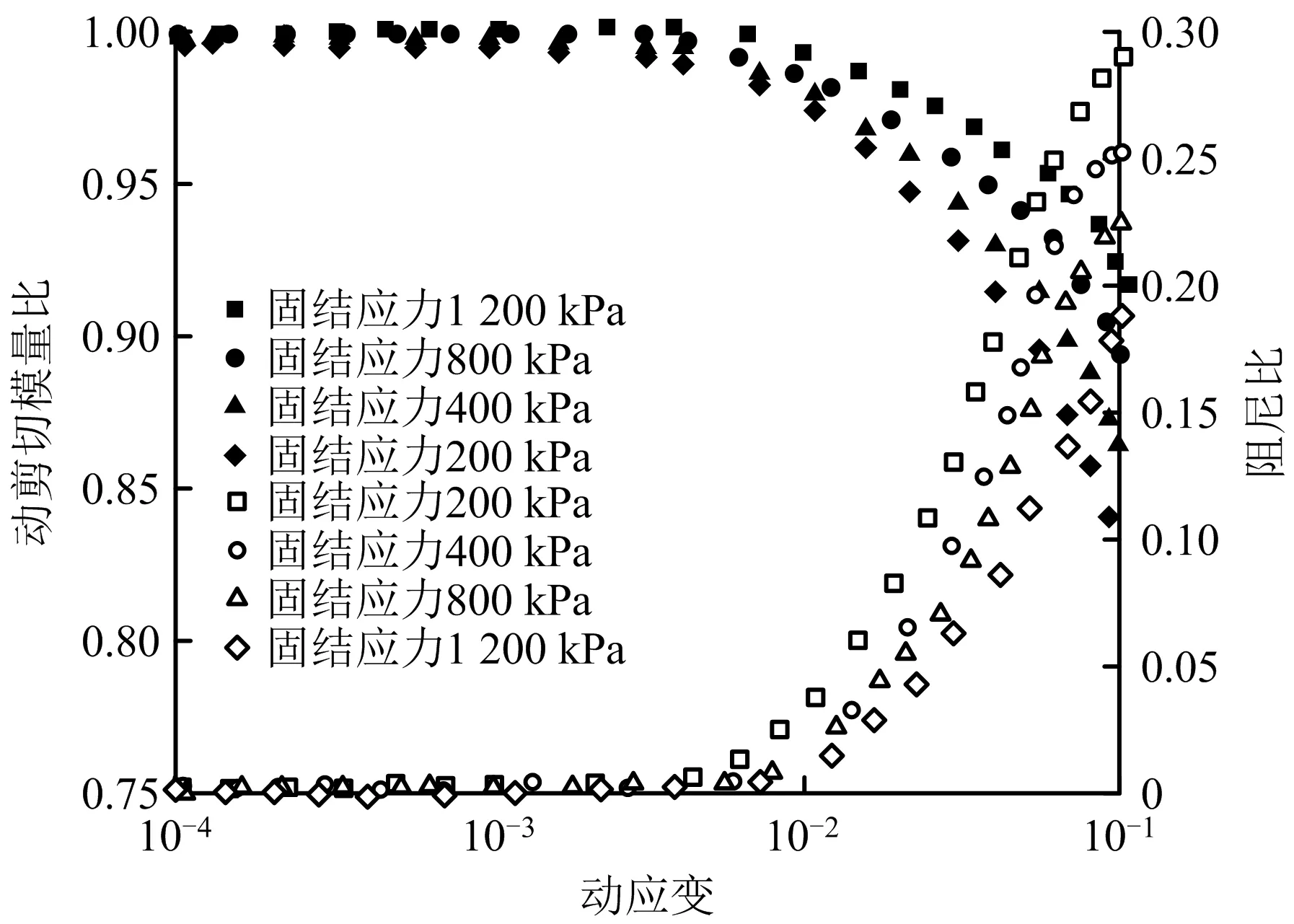
图9 方案1动剪切模量比、阻尼比与动应变关系Fig.9 Relationship between dynamic shear modulus ratio,damping ratio and dynamic strain in scheme 1
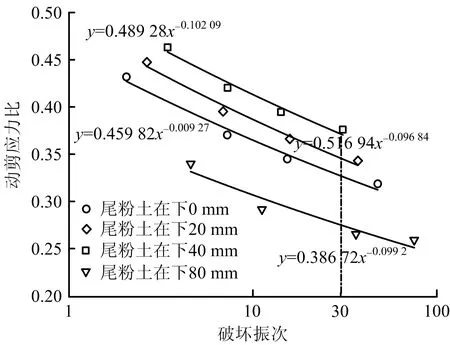
图10 方案2动剪应力比与破坏振次关系Fig.10 Relationship between dynamic shear stress ratio and failure vibration times in scheme 2
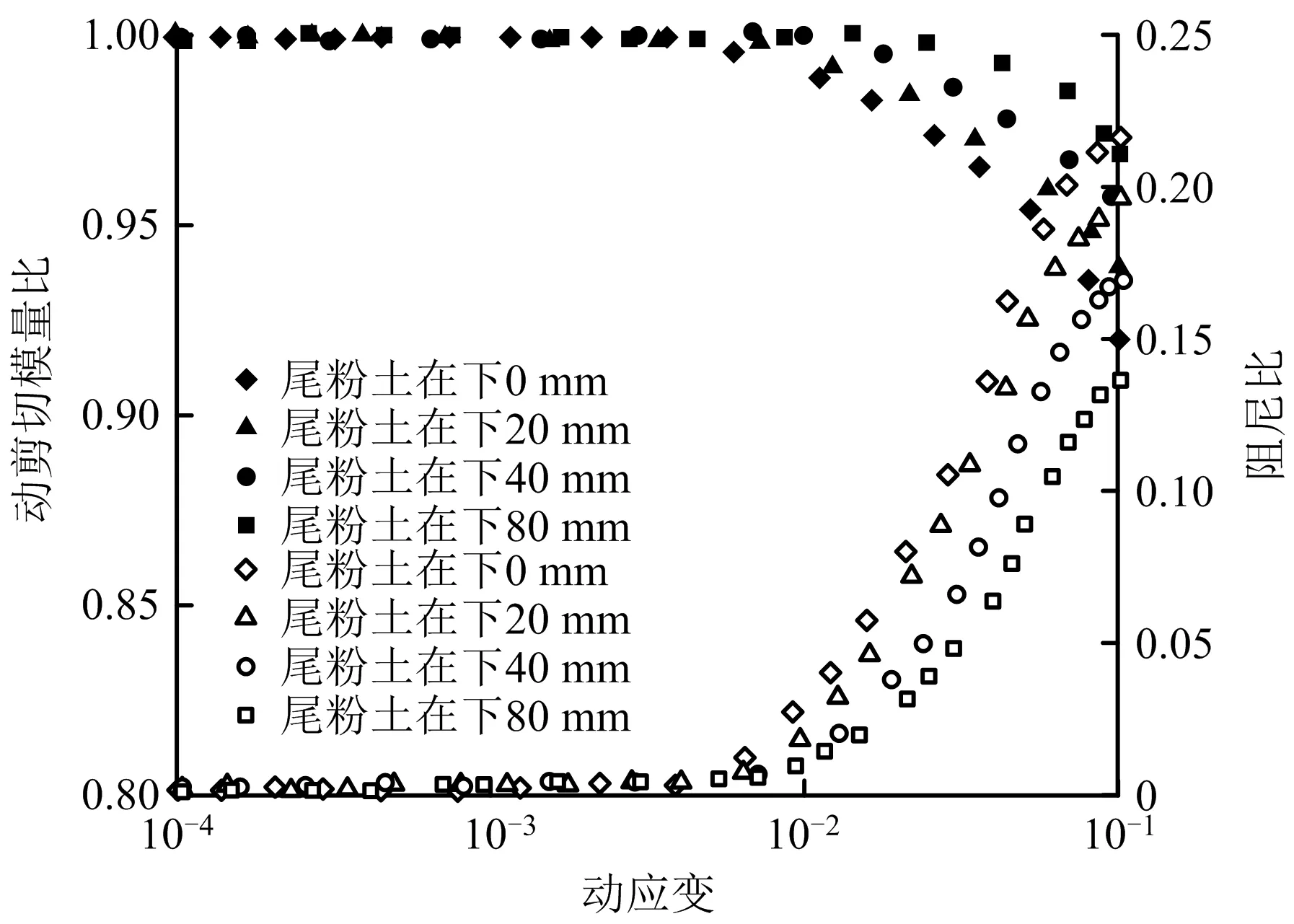
图11 方案2动剪切模量比、阻尼比与动应变关系Fig.11 Relationship between dynamic shear modulus ratio,damping ratio and dynamic strain in scheme 2
2.4 动孔压变化趋势
文献[19]通过研究饱和砂土动三轴试验发现,动孔压比与破坏振次周期比呈“S”型曲线,动孔压增长规律如式(16)所示:
(16)
式中:p为动孔隙水压力kPa;N为破坏振次周期数;NL为液化破坏时振次;σc′为有效固结应力,kPa;α为试验常数,取2.0~3.0。
固结应力大小为试样固结时围压与反压差值,试样反压均为200 kPa,不同固结应力下试样破坏时围压分别为400,600,1 000,1 400 kPa。
方案1、2动孔压演化趋势如图12~13所示。由图12~13可知,当固结比Kc=1时,方案1、2动孔压变化趋势总体为“S”型反正弦函数;随振动次数增加,动孔压逐渐接近围压,试样破坏。由图12可知,随固结应力增大,初始阶段动孔压增长斜率变小,曲线整体变化趋势更明显,说明层状尾砂动孔压对固结应力变化较敏感;由图13可知,在高固结应力下,层状试样动孔压随尾粉土厚度增加,稳定增长阶段延长,这是因为尾粉土内部结构更紧密,产生超孔隙水压,尾粉土阻隔超孔隙水压力上升作用更明显。尾粉土越多,达到液化所需振动次数增加;尾粉土下厚度不同时,对应破坏振次分别为61,70,77,86次,这是由于尾砂内部力链较强,可承担外部施加荷载力,在前期固结过程中,细小颗粒位置因固结应力作用相互移动,随振动次数增加,尾矿颗粒内部结构越来越稳定,在高振幅低振次动荷载作用下,力链架构受振动幅度影响,产生惯性力和破坏力,又因尾矿粒径大小与组成结构排序差异,使尾细砂与尾粉土上作用力大小、方向产生差异;尾粉土厚度不同,使不同层状尾砂下动孔隙水上升趋势改变,在高固结应力作用下,颗粒间排列移动速度较快,因接触状态较快改变,产生脱离接触,使达到稳定力链所需振动次数增加。
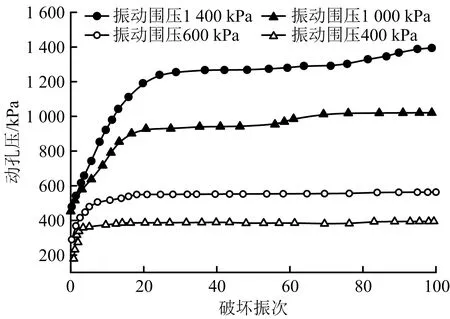
图12 方案1动孔压演化趋势Fig.12 Evolution trends of dynamic pore pressure in scheme 1
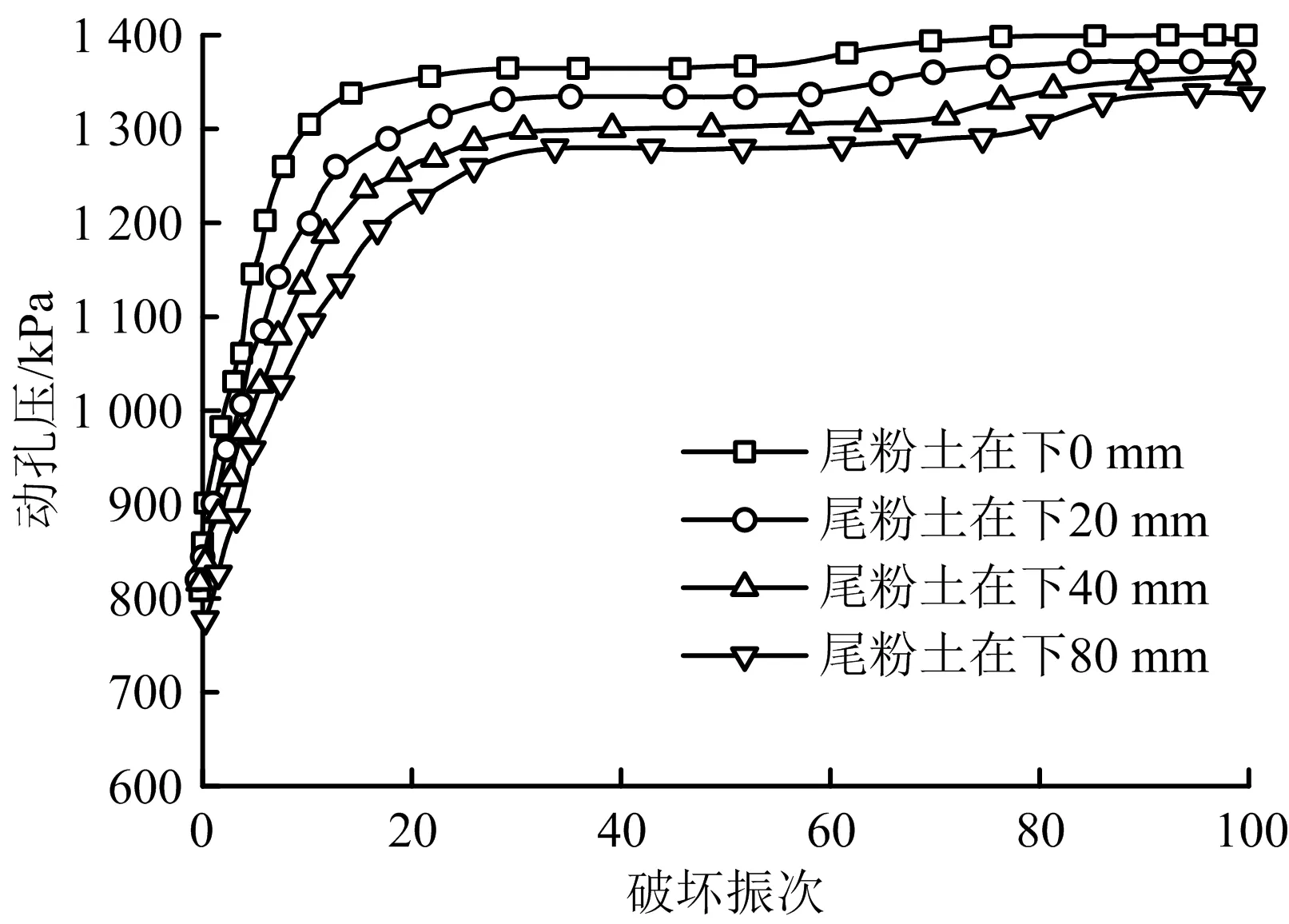
图13 方案2动孔压演化趋势Fig.13 Evolution trends of dynamic pore pressure in scheme 2
3 结论
1)当尾粉土厚度不变时,随固结应力增大层状尾砂动弹性模量变大,动应变增大到一定幅值迅速下降后趋于0;动弹性模量倒数与动应变呈线性关系,直线斜率变小;动剪应力比与破坏振次呈幂函数关系,动剪应力比降低,曲线出现归一趋势;在同一动应变幅值下,动剪切模量比更大,阻尼比更小。
2)当固结应力不变时,随尾粉土厚度增加:层状尾砂动弹性模量变小,动应变达到一定幅值时,迅速下降后趋于0;动弹性模量倒数与动应变关系曲线斜率变大;动剪应力比先上升后下降,尾粉土厚度对动剪应力比与破坏振次关系有一定影响;在同一动应变幅值下,动剪切模量比变大,阻尼比变小。
3)固结应力变化能直接反应动孔压变化趋势,随固结应力增大,初始增长斜率下降。
4)尾粉土对动孔压阻隔作用大于尾细砂;随尾粉土厚度增加,试样发生破坏所需振动次数增加。
