零能耗光伏并网建筑的奖惩机制建立和应用研究*

安徽工业大学 孙瑞瑞 鲁月红 季海霞 黄志甲

0 引言

随着发展中国家经济水平的不断提高，建筑行业能耗将快速增长，预计到2040年，将占能源消费总量的1/3，新增的能耗几乎全部是电耗[1]。联合国第五次气候变化评估报告显示，建筑行业碳排放量占全球碳排放量的70%[2]，因此，建筑行业应对全球高碳排放量负主要责任。不断增长的电力消费是将能源与环境领域问题相联系的一个重要促成因素。在这一背景下，绿色建筑和零能耗建筑的推广对建筑节能减排及可持续发展具有促进作用。

近年来，中国、德国、英国、丹麦等国家在可再生能源技术的发展与应用方面进行了大量的研究[3-6]。财务激励政策，如投资补贴、净计量方案和上网电价补贴，被认为是可再生能源获得广泛应用的主要促进因素。2013年，我国出台了统一的光伏上网电价补贴政策，随后又推出了区域上网电价补贴政策(feed-in tariff, FIT)[7-8]。Winter等人对2010—2017年德国家庭电费支出进行了分析，发现装有光伏系统的用户通过FIT政策获得的收益不仅能补偿逐年增长的可再生能源附加费，而且能获得一定的净收入[9]。2010年以来，英国实行的FIT政策有效促进了小型光伏系统(≤10 kW)在住宅中的应用，至2016年累计装机量已达2 GW，且光伏安装成本的下降将驱动这一数字快速增长[10]。Ritzenhofen等人通过量化FIT等级之间的关系，评估了实施不同FIT方案对可再生能源投资倾向的影响[11]。

在实现建筑零能耗目标过程中，利用集成于建筑中的可再生能源系统现场发电是目前应用最多的方案[12-13]。零能耗建筑的一个基本要求是建筑的现场发电量至少要满足自身用电需求[14-15]。目前主要通过被动式设计(围护结构、建筑朝向等)、主动式系统优化(HVAC系统能效、照明功率等)和可再生能源利用(光伏发电板、风力发电机等)实现建筑的零能耗[16]。对建筑用户来说，零能耗建筑初投资是制约其是否安装可再生能源系统的主要因素。由于可再生能源发电政策逐步进入补贴退坡阶段，用户对可再生能源系统的投资收益也越来越少，使得建筑年发电量难以与年能耗之间达到平衡[17]。为解决这一问题，Lu等人在建筑总成本中引入奖惩成本，加入奖惩成本后安装了可再生能源系统并达到零能耗目标的建筑最终总成本仅为无可再生能源系统时的1/3[18]。奖惩机制(reward-penalty mechanism，RPM)不仅可以降低可再生能源发电拍卖风险[19]，而且可以缓解可再生能源系统过度发电的问题[9]。若建筑用户能在给定的时间内达到目标要求，将会得到一定的奖金，否则将被罚款。因此，合理的奖惩机制能保证最低投资成本下的可再生能源系统可靠运行。

本文以上海地区某居住建筑为研究对象，建立奖惩函数并将其应用于零能耗建筑的设计中，通过给予达到零能耗目标的建筑用户一定的奖金或对非零能耗建筑用户收取一定的罚金，从而实现建筑的环境友好性，并在经济上达到最优。

1 研究方法

1.1 确定问题

FIT政策是促进可再生能源技术发展的有效措施。然而，在上网电价补贴逐年减少的情况下，潜在的可再生能源系统用户对于需要安装多少光伏板(PV)或风力发电机(WT)以获得最大的经济效益存在疑惑。因此，可以建立一个与零能耗等级有关的奖惩机制，为建筑用户提供优化的可再生能源系统方案并分析建筑用户在该奖惩机制下的经济效益。

零能耗等级定义为建筑现场光伏全年发电量与标准建筑年能耗之比：

(1)

式中Rz为零能耗等级；EP为建筑现场光伏全年发电量，kW·h/a；Eb,s为标准建筑年能耗，kW·h/a。

Rz越大，表示零能耗等级越高，例如，Rz=1.0表示建筑全年光伏发电量等于建筑年能耗，用1.0ZEB(zero energy building level)表示。标准建筑指某一类型建筑中具有典型代表的建筑，标准建筑能耗Eb,s为建筑各用电设备逐时能耗之和。

1.2 技术路线

本文以上海地区某居住建筑为例，建立适用于并网光伏居住建筑的奖惩机制，具体路线如图1所示。

1) 确定标准建筑能耗。可通过2种方法获得标准建筑能耗，第1种是通过建筑能耗数据库获得建筑的能耗数据；第2种是基于当地典型气象参数和相关建筑参数，将模拟的建筑能耗作为标准建筑能耗。

2) 确定奖惩函数中的未知参数。首先，根据建筑能耗与光伏发电量之间的关系，对建筑进行零能耗等级划分，并计算对应的光伏板数量。其次，根据当前光伏板与电力的市场价格，确定光伏系统年均初投资与标准建筑的运行费用，两者之和为建筑的常规总成本。再次，将常规总成本与零能耗等级进行曲线拟合，得到常规总成本的拟合函数。最后，假设奖惩函数为与零能耗等级有关的一元二次函数，根据方案制定者给予的3个初始条件，对奖惩函数中的未知数进行求解。

3) 验证奖惩函数。利用蒙特卡罗方法模拟不同建筑能耗数据，或从现有的建筑能耗数据库中选取不同的建筑，用以验证奖惩函数的适用性。

1.3 奖惩函数

在本文中，奖惩机制是基于标准建筑建立的。考虑温度的影响，i时刻光伏板输出功率与入射到光伏板上的太阳辐照度成正比，有下式：

[1+kp(tC,i-tSTC)]

(2)

式中SP为光伏装机容量,kW；Wp,i为1 kW装机容量光伏板i时刻的实际输出功率，kW/kW；YP为1 kW装机容量光伏板的峰值功率，kW；fp为降额因子，取0.9；IT,i、IS分别为i时刻和标准工况下光伏板处的太阳辐照度，kW/m2；kp为温度系数，%/℃；tC,i、tSTC分别为i时刻和标准工况(25 ℃)下光伏板温度，℃。

建筑在i时刻与电网交换的电量为建筑逐时能耗与光伏发电量之差。建筑的运行费用为建筑运行期间电网向建筑提供电量的费用，初始成本为光伏板的年均初投资，常规总成本为运行费用与初投资之和：

Cio=Ci+Co

(3)

式中Cio为建筑常规总成本，元/a；Ci为光伏年均初投资，元/a；Co为建筑运行费用，元/a。

对常规总成本与零能耗等级之间的关系进行拟合，得到：

(4)

式中a1、b1、c1为得到的拟合常规总成本函数中的已知系数和常数。

假设在建筑年成本中引入由奖金或罚金组成的奖惩成本，则建筑总成本包括常规总成本与奖惩成本两部分：

(5)

(b1+b2)Rz+(c1+c2)

(6)

式(5)、(6)中Crp为奖惩成本，元/a；a2、b2、c2为奖惩成本函数中的未知系数和常数；Ct为建筑总成本，元/a。

根据加入奖惩成本后的建筑总成本与常规总成本之间的关系，提供3个初始条件用于求解总成本函数式(6)中的未知参数。初始条件为

Rz=0,Ct=k1Cio

(7)

Rz=1.0,Ct=k2Cio

(8)

Ct,min=Ct|Rz=r

(9)

式(7)～(9)中k1为建筑无可再生能源系统(0ZEB)时的总成本与该建筑常规总成本的比值；k2为零能耗建筑(1.0ZEB)的总成本与该建筑的常规总成本之比；Ct,min为建筑最小总成本，元/a；r为建筑最小总成本对应的零能耗等级。

通过观察奖惩函数在总成本调节中的作用对其效果进行评估，引入总成本变化率σ：

(10)

σ值为负/正表示此时建筑用户会收到奖金/罚金，绝对值越大，奖金/罚金越高，对成本的调节作用越明显。

用误差指标δ对奖惩函数在不同能耗建筑中的应用效果进行评估，其计算式为

(11)

式中C′t为建筑在r零能耗等级下的总成本，元/a。

δ绝对值越小表示奖惩函数越适用该能耗的建筑。

1.4 蒙特卡罗模拟

为验证所建立的奖惩机制对不同能耗建筑的适用性，提出建筑能耗等级Rb的概念，并将其定义为建筑k的年能耗Eb_k与标准建筑能耗Eb,s之比：

(12)

本文选取9个不同的建筑能耗等级(building energy consumption level，BEC)，采用蒙特卡罗方法模拟各建筑能耗等级下的逐时能耗，用以验证奖惩函数在不同建筑能耗中的有效性。

在本研究中，假设建筑k在i时刻的能耗Eb_k,i服从正态分布，其中标准偏差为平均值的20%，如式(13)所示：

Eb_k,i～N{(Eb,s)i,[0.2(Eb,s)i]2}

(13)

2 应用分析

本文选择一栋位于上海市的2层住宅(见图2)为标准建筑，建立奖惩函数并研究其有效性。该建筑坐北朝南，占地100 m2，屋顶为30°倾斜的砖瓦结构。上海市处于夏热冬暖地区，年太阳总辐射量差异较小。建筑内的电器有照明设备、电视机、计算机、洗衣机等。各电器的使用情况设定如表1所示，其中空调器在室外温度高于30 ℃或低于10 ℃时开启。本文选择的光伏板初投资、运行成本分别为2 250元/kW和0，电池组件的标称工作温度为47 ℃，标准工况下的转化效率为18%。假设光伏组件寿命为25 a，降额因子为0.9。光伏板设计角度固定为30°，单块板的面积为1.64 m2。

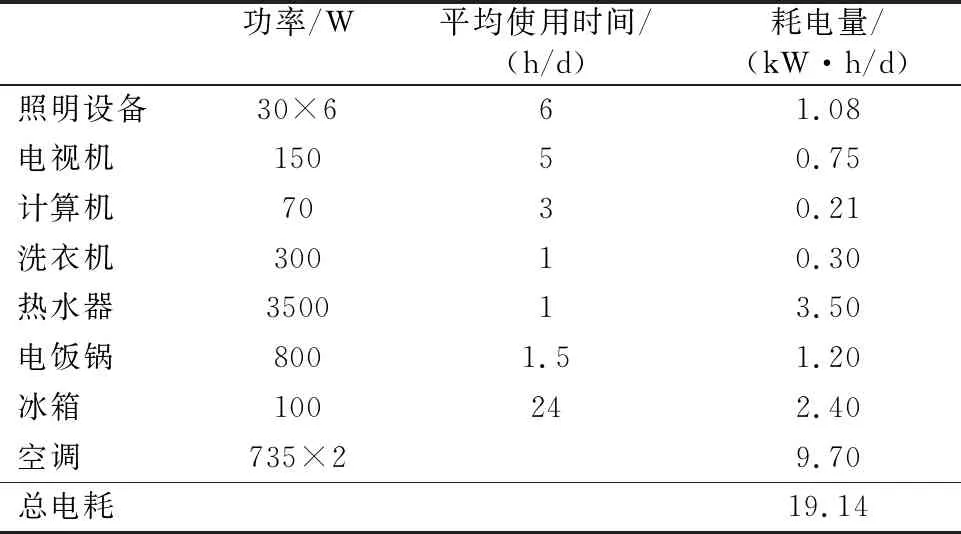
表1 电器使用情况

室外温度和太阳辐射是影响建筑能耗和光伏发电的重要因素，上海市月平均太阳辐射和环境温度如图3所示，日平均辐照量为3.62 kW·h/m2，日平均环境温度为16.9 ℃，室外最高温度为37.3 ℃，最低温度为-4.7 ℃。基于表1中电器使用情况模拟的全年建筑能耗为6 983.9 kW·h，每月能耗如图4所示。

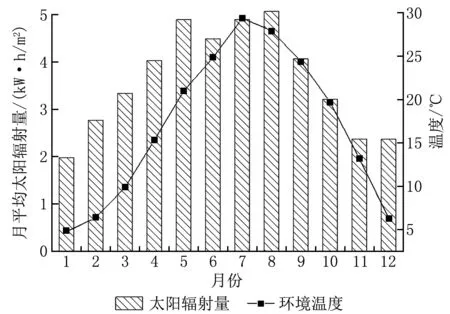
图3 月平均太阳辐射量和环境温度

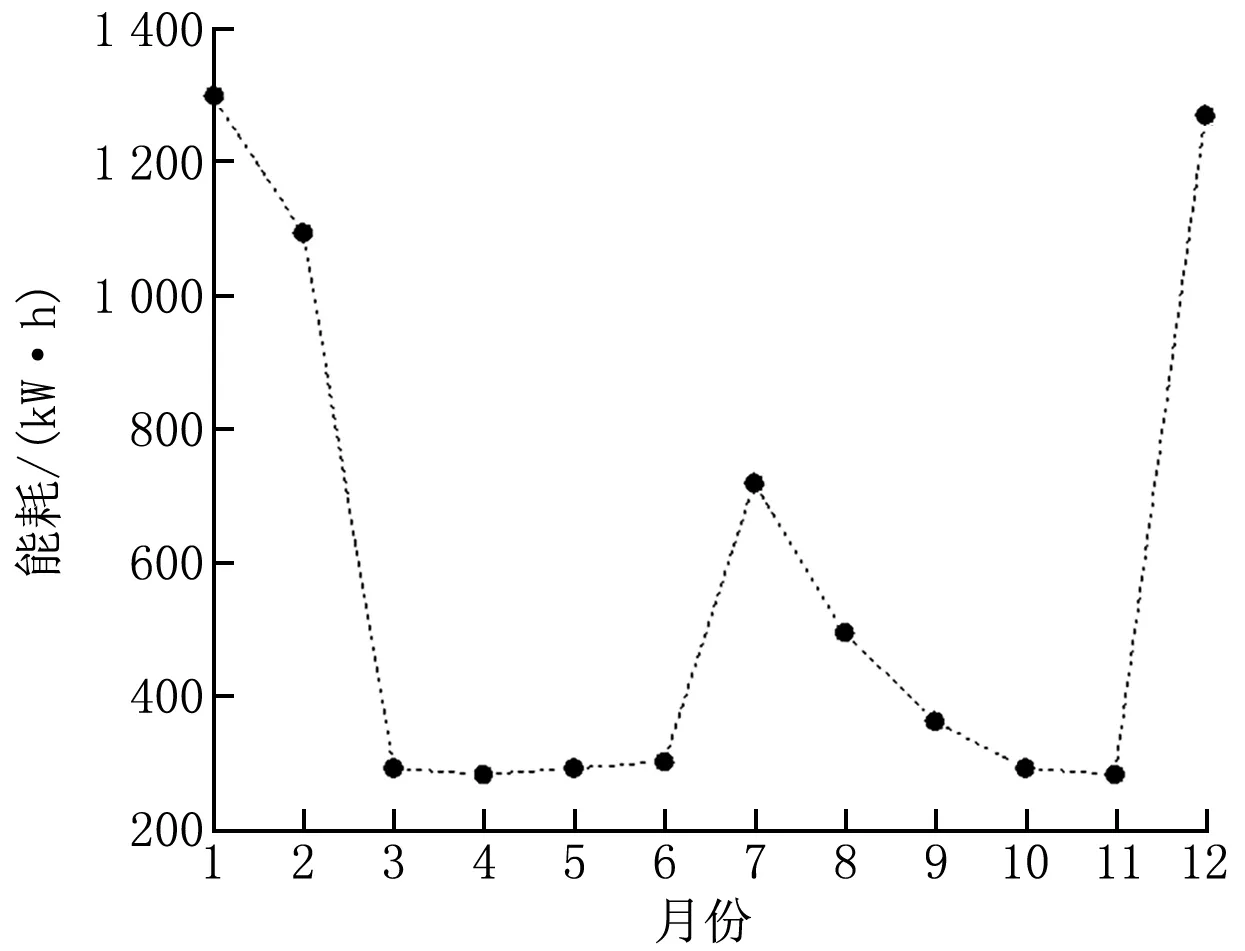
图4 建筑月能耗

3 结果和分析

本文设计了S0、S1、S23种奖惩方案，通过对比选择最优方案。各方案对应的初始条件中k1、k2、r值见表2。基于以上假设可求解式(5)中的未知参数a2、b2、c2。

表2 3种方案设定值

3.1 确定奖惩函数

根据表2中的假设，求解各方案奖惩函数中的未知参数，并确定奖惩函数的具体形式，如表3所示。为了验证本文中基于标准建筑能耗设计的奖惩函数的适用性，将其应用于不同零能耗等级(0ZEB、0.2ZEB、0.4ZEB、0.6ZEB、0.8ZEB、1.0ZEB、1.2ZEB)和建筑能耗等级(0.4BEC、0.6BEC、0.8BEC、1.0BEC、1.2BEC、1.4BEC、1.6BEC、1.8BEC、2.0BEC)组合下的建筑，研究其对建筑总成本的影响。

表3 各方案奖惩函数具体形式

3.2 不同参数对建筑总成本的影响

1) 零能耗等级对建筑总成本的影响。

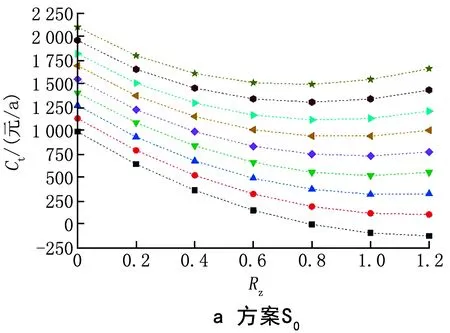
建筑总成本与其零能耗等级密切相关，图5显示了标准建筑Rb,s=1.0时总成本与零能耗等级之间的关系。从图中可以看出，在没有奖惩机制的情况下，建筑常规总成本随零能耗等级的增大而增加；当引入奖惩机制时，3种方案下的总成本曲线均为凹形曲线，且分别在1.0ZEB、1.0ZEB、0.8ZEB处取得最低总成本，分别为512.5、0、476.8元/a。同时，可以预测总成本在达到最低点之后，将会随着零能耗等级的增大而增加。

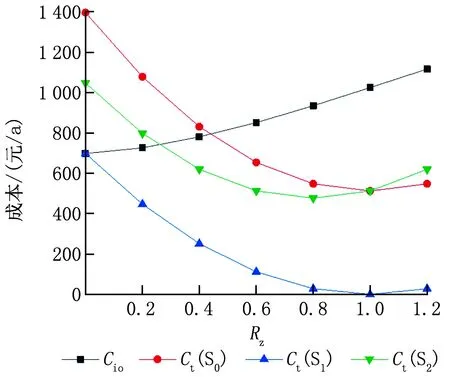
图5 标准建筑(Rb,s=1.0)总成本与零能耗建筑等级之间的关系

此外，与常规总成本相比，不同零能耗等级下的总成本变化率是不同的，如表4所示。S0、S1和S23种方案下的成本变化率σ区间分别为-50.9%～100%、-97.5%～100%、-50.0%～50.0%。同时，方案S0、S1、S2可分别在0.6ZEB、0.2ZEB、0.4ZEB 的设计中获得奖金，且建筑的零能耗等级越高，建筑用户的经济效益越高。

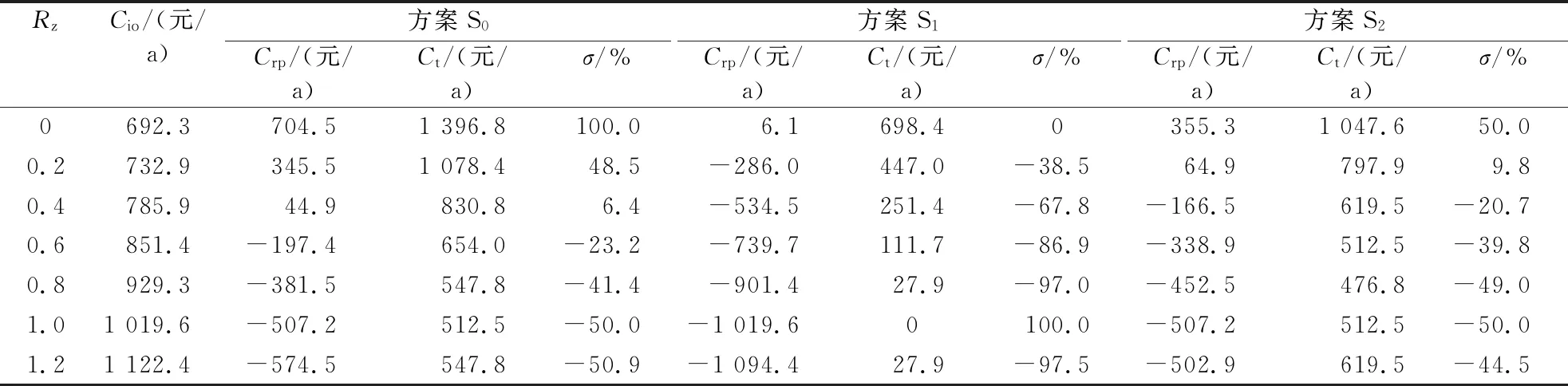
表4 各方案下不同零能耗等级建筑的总成本变化率

2) 建筑能耗等级对建筑总成本的影响。

为了进一步确定奖惩函数对非标准建筑总成本的影响，分析Rz=1.0时建筑总成本与能耗等级(0.4BEC～2.0BEC)之间的关系。如图6所示，在引入奖惩函数后，3种方案下的总成本曲线与常规总成本曲线变化趋势一致，均与能耗等级成正比。且方案S0和S2的总成本曲线重合，这是由于2个方案下的k2值相同。

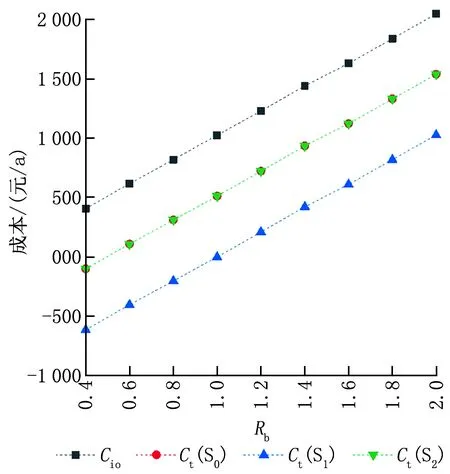
图6 Rz=1.0时建筑总成本与建筑能耗等级之间的关系

表5显示了不同能耗等级的建筑总成本及成本变化率比较。在3种方案中，各能耗等级的总成本均低于常规总成本，总成本变化率区间分别为-124.5%～-24.8%、-250.3%～-49.8%、-182.3%～-24.8%；且成本变化率随着能耗等级的增大而减小，因此，当超过某一能耗等级时，奖惩函数就失去了作用。

表5 各方案下不同能耗等级建筑的总成本及成本变化率

3) 零能耗等级和建筑能耗等级对建筑总成本的影响。

同时考虑零能耗等级与建筑能耗等级2个因素，研究3种方案下奖惩机制在2种因素都变化时对建筑总成本的影响，如图7所示。在3种方案的奖惩机制下，不同建筑能耗等级下的建筑总成本变化趋势基本一致。同一建筑能耗等级下，建筑总成本先随着零能耗等级的增大而减小，到达某一值后随着零能耗等级的增大而增大；同一零能耗等级下，不同建筑能耗等级建筑的总成本也存在差异，这是由不同的初投资与运行费用导致的。理想情况下，方案S0中不同能耗等级的建筑，最低总成本对应的零能耗等级应为1.0ZEB。经过分析发现，建筑能耗等级在0.4BEC～0.6BEC、0.8BEC～1.4BEC和1.6BEC～2.0BEC时，建筑总成本曲线的最低点分别位于1.2ZEB、1.0ZEB和0.8ZEB处，均位于1.0ZEB附近，因此，可以认为奖惩函数适用于能耗等级为0.4BEC～2.0BEC的建筑。

3.3 验证奖惩函数

本文基于某一特定的标准建筑建立了3个奖惩函数，研究了各奖惩函数在不同零能耗等级和建筑能耗等级下对建筑总成本的影响。为了验证并量化奖惩函数在不同类型建筑中的应用有效性，选择了9个建筑能耗等级，在每个建筑能耗等级下，利用蒙特卡罗方法模拟建筑能耗100次，并取平均值作为一个建筑能耗样本。图8显示了9个建筑能耗级别下48 h的平均逐时能耗。

图8 蒙特卡罗方法得到的9个建筑样本48 h的逐时能耗

如表6所示，方案S0中，当引入奖惩机制时，建筑的最小总成本预计发生在1.0ZEB处，建筑能耗等级在0.4BEC～0.6BEC、0.8BEC～1.6BEC、1.8BEC～2.0BEC的建筑最小总成本分别发生在1.2ZEB、1.0ZEB和0.8ZEB处，除能耗等级为0.4BEC(δ=31.51%)和0.6BEC(δ=-11.42%)的建筑成本误差较大外，其他能耗等级的建筑成本误差均保持在4%以内。方案S1中，建筑最小总成本预计发生在1.0ZEB处，能耗等级在0.4BEC～0.8BEC、1.0BEC～1.2BEC、1.4BEC～1.8BEC、2.0BEC的建筑最小总成本分别发生在1.2ZEB、1.0ZEB、0.8ZEB和0.6ZEB处，除能耗等级在2.0BEC时偏离预计值较大外，其他均位于1.0ZEB附近，且各能耗等级的成本误差均低于7%。方案S2中，建筑最小总成本预计发生在0.8ZEB处，能耗等级在0.4BEC～0.6BEC、0.8BEC～1.2BEC和1.4BEC～2.0BEC的建筑最小总成本分别发生在1.0ZEB、0.8ZEB和0.6ZEB处，除能耗等级为0.4BEC的建筑误差为24.04%外，其他能耗等级的建筑成本误差均低于4%。因此，当奖惩函数应用于能耗等级为0.8BEC～1.8BEC之间的建筑时是有效的。

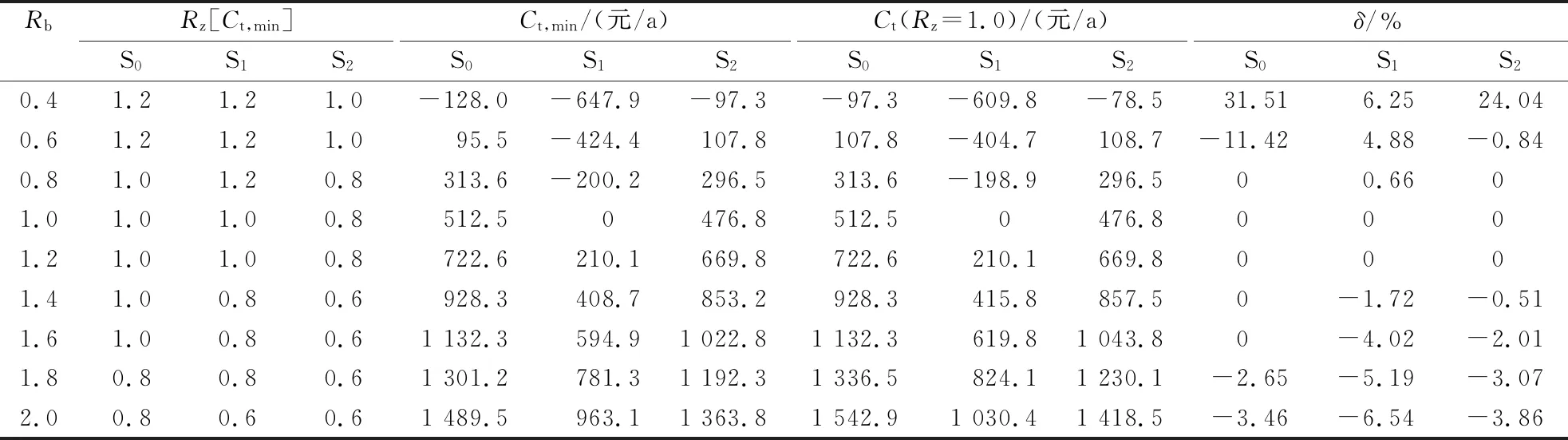
表6 奖惩函数在不同能耗等级建筑中的应用有效性

3.4 奖惩机制的应用

可将本文设计的奖惩函数应用于单个居住建筑光伏系统的设计中，如图9所示。首先，用户可以利用能耗数据库或能耗模拟方法获得该建筑的年能耗，并根据自身需求选择合适的零能耗等级，设计并选择对应的光伏板数量。其次，计算光伏板所需的安装面积、光伏板年初投资及建筑运行费用，并利用奖惩函数计算奖惩成本，进而获得该建筑的总成本。最后，根据光伏板安装所需面积和建筑总成本进行评估，若两者均能被接受，则可通过该设计方案；否则，重新选择光伏板数量，并重复以上步骤直到两者均满足要求。以标准建筑为例，零能耗等级为0ZEB、0.2ZEB、0.4ZEB、0.6ZEB、0.8ZEB、1.0ZEB、1.2ZEB时，所需的光伏板安装面积分别为0、8.20、14.76、21.32、27.88、36.08、42.64 m2。

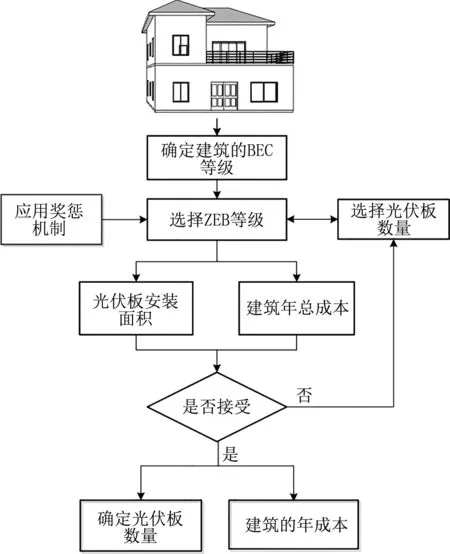
图9 奖惩机制的应用流程图

4 结语

本文提出了一种零能耗建筑奖惩机制设计方法，通过在常规总成本中增加奖惩成本，从而将其调整为满足设计者需求的成本优化函数，并采用蒙特卡罗方法验证了奖惩函数在不同建筑能耗下对总成本调节的有效性。

以上海市某居住建筑为例，设计了3种不同的奖惩方案(S0、S1、S2)。当零能耗等级为1.0ZEB时，3种方案下的建筑总成本与常规总成本相比分别降低了50%、100%和50%。能耗等级从0.4BEC变化到2.0BEC时，3种方案下的总成本变化率区间分别为-124.5%～-24.8%、-250.3%～-49.8%、-182.3%～-24.8%，从而证明了通过引入奖惩函数可以对建筑总成本进行很好的调节，且其适用于能耗等级介于0.8BEC～1.8BEC的建筑。此外，当奖惩函数应用于不同的建筑能耗等级时，方案S1中的奖惩函数比方案S0和S2可应用的建筑能耗等级范围更广。

本文通过设计和证明引入的一元二次奖惩函数在建筑中的应用，旨在进一步推动零能耗建筑的发展。后续研究将从不同类型奖惩函数的设计和应用方面展开。