时变极化编码表面及其在无线通信中的应用

胡 琪 陈 克 郑依琳 徐之源 王 健 赵俊明 冯一军

(南京大学电子科学与工程学院 南京 210023)

1 引言

作为电磁超构材料的二维形式，电磁超构表面由亚波长尺寸的单元在平面内以周期性或非周期的方式排布而成。与超构材料相比，超构表面的体积和重量均大幅缩减，且同时具备低剖面、低损耗和低成本等优点。利用超构表面可实现对电磁波幅度、相位和极化等基本特性的灵活调控，因此许多奇异的物理现象和多功能器件应运而生，例如异常折射/反射[1]、波束赋形[2]和超透镜[3]等。在超构表面结构中集成如开关二极管、变容管和石墨烯等有源器件，并通过外部电路控制有源器件的工作状态，可实时调控超构表面的电磁响应，进而实现对电磁波的可重构聚焦[4]、波束调控[5,6]和极化转化[7,8]。这类超构表面通常称为有源编码超构表面[9]。与无源超构表面相比，有源超构表面可利用其动态电磁响应特性和时分复用技术实现更灵活的电磁波调控，因此在实际应用中具有更好的应用前景。

电磁波的非线性调制广泛应用于光存储、通信等领域。目前，微波波段和光波段均可实现对电磁波的非线性调制，例如，借助高非线性介质的等离子激元超构表面可以调控电磁波二次谐波的波前[10]。最近，研究学者在空间编码超构表面的基础上提出的时-空间编码超构表面，可根据预先设计的编码序列周期性地切换有源器件的工作状态。基于傅里叶变换原理，该周期性的调制信号将引入新的谐波频率分量，因此，通过这一新增时间维度，可同时非线性地调控电磁波基波和谐波的波前[11–13]。例如，利用傅里叶变换与卷积原理搬移超构表面的散射方向图，电磁波谐波波束可被偏转至任意角度[14]。已有研究表明应用时变编码超构表面可形成新型超构表面无线通信系统[15–17]，且同时具备简化通信系统结构和高效传输实时信号的优点。目前，超构表面无线通信系统主要采用相位调制方式，包括二进制相移键控(Binary Phase-Shift Keying,BPSK)[18]、正交相移键控(Quadrature Phase-Shift Keying,QPSK)[19]和8相移键控(8 Phase-Shift Keying,8PSK)[20]等。作为另一种调制手段，幅度调制(Amplitude Modulation,AM)具备强抗干扰能力和低失真的优点也广泛应用于信号无线传输。

本文提出了一种时变极化编码表面的分析和设计方法，并通过时域信号的变化产生新的谐波分量，进而实现对入射电磁波的非线性调控。具体而言，通过现场可编程门阵列(Field Programmable Gate Array,FPGA)输出电压控制超构表面的工作状态，并利用时域变化的方波信号作为调制信号，通过调节方波信号的占空比与频率，进而按需实现反射电磁波在频谱上的能量、频率分布与偏移。在此基础上，进一步探讨了时变极化编码超构表面的实际应用，提出了一种基于二进制幅移键控(Binary Amplitude-Shift Keying,BASK)调制方式的无线通信系统。所有测试结果均与理论计算结果吻合良好。本文提出的极化编码设计方法也有望在量子通信、高分辨率成像等领域发挥重要作用。

2 时变编码调制理论

假设反射式时变编码二维超构表面由M×N个可编程单元构成，其中所有单元均处于相同的工作状态且均加载了有源可调元件。通过改变外部控制电路加载至有源器件的驱动电压，单元的反射系数将随驱动电压实时切换，从而形成对超构表面的时变编码调制[21]。高速响应的有源器件可确保超构表面的反射系数受外部控制信号实时调控，从而令超构表面在如无线通信等实际领域中得以应用。假设周期性时变编码调制频率远小于入射载波频率，当单频正弦波以频率fc入射至时变编码超构表面时，反射波Er(t)可表示为

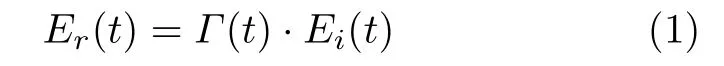
其中，Ei(t)=Acexp(–j2πfct)为入射载波；Γ(t)为以时间T0为周期的反射系数，且在一个周期内可表示为一系列脉冲信号的线性组合，如式(2)所示

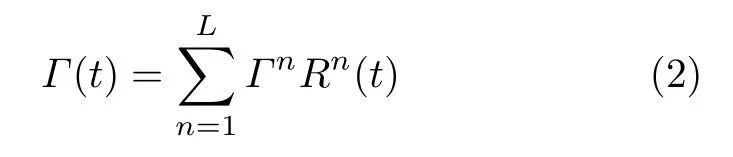
其中，L为时变调制信号在一个周期内编码序列的长度；Rn(t)函数为一系列脉冲宽度τ=T0/L的脉冲函数的线性组合，它以时间T0为周期，且仅在时间间隔(n–1)τ≤t≤nτ内取值为1，而在其他时刻均取值为0；Γn=Anexp(jφn)为超构表面单元在时间间隔(n–1)τ≤t≤nτ内的反射系数，An和φn分别对应该时间间隔内反射系数的幅度与相位。

为了观察时变调制信号在频域内对电磁波基波和谐波的调制方式，我们将周期性反射系数Γ(t)以傅里叶级数形式展开，可表示为

其中，m为谐波阶数；ω0=2πf0=2π/T0为时变调制信号的频率；1/L=τ/T0为一个周期内单个脉冲信号占调制信号的比例。再对式(1)作傅里叶变换，则反射波可在频域表示为

由此可见，在载波以频率fc入射时周期性地调控超构表面的反射系数，可产生一系列以载波频率fc为中心频率的谐波分量fc+mf0；同时，通过周期性地切换驱动电压等手段可调节等效反射系数am，从而可以非线性地调控基波与谐波的反射幅度与相位。

以如图1所示的占空比为S、周期为T0的方波为例，若将占空比定义为高反射状态占一个周期的百分比，那么超构表面在该时变方波信号调制下，一个周期内的同极化反射系数的表达式为

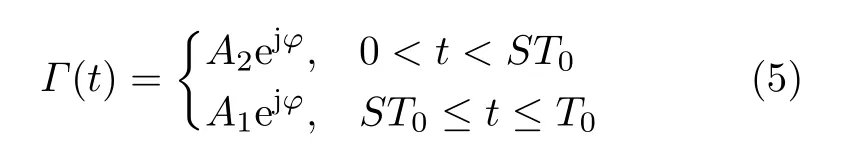
其中，可编程单元在该时变信号调制下的两种同极化反射系数分别为Γ1=A1exp(jφ)和Γ2=A2exp(jφ)，这两种反射系数具备不同的反射幅度A1与A2和相同的反射相位φ，且可分别由1比特二进制编码表示为“0”和“1”，其余能量被转极化后反射。在方波调制下，将式(5)代入式(3)和式(4)中，同极化反射波在频域的表达式可进一步化简为

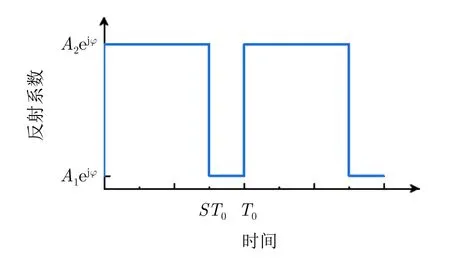
图1 基于幅度调制的时变方波调制信号示意图Fig.1 Square-wave-type time-varying signals used for AM

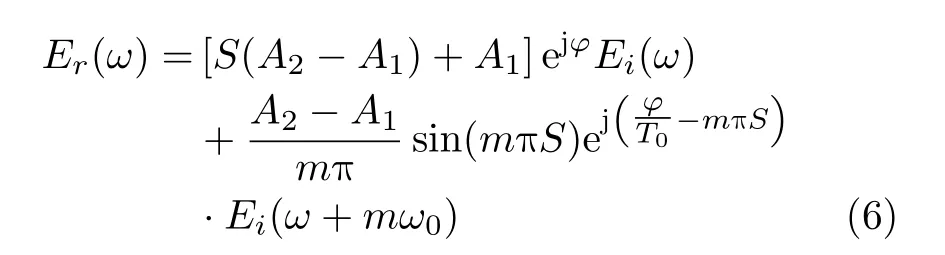
由式(6)可见，在加载时变方波信号条件下，经转极化超构表面反射后的电磁波基波与谐波响应将发生变化。具体地，令m=0，可得出其基波的反射相位为恒定值exp(jφ)，而反射幅度为[S(A2–A1)+A1]，与占空比S呈线性单调递增的关系，即占空比越大，基波的幅度越高；m阶谐波幅度为(A2–A1)sin(mπS)/mπ、相位为exp(jφ/T0–mπS)，与谐波阶数m和占空比S均呈非线性相关，同时，m阶谐波幅度(A2–A1)sin(mπS)/mπ为关于谐波阶数m的偶函数，因此，在方波信号调制下，超构表面在频域内基波与谐波的能量应以基波频率fc为轴呈对称分布。

3 超构表面单元结构设计

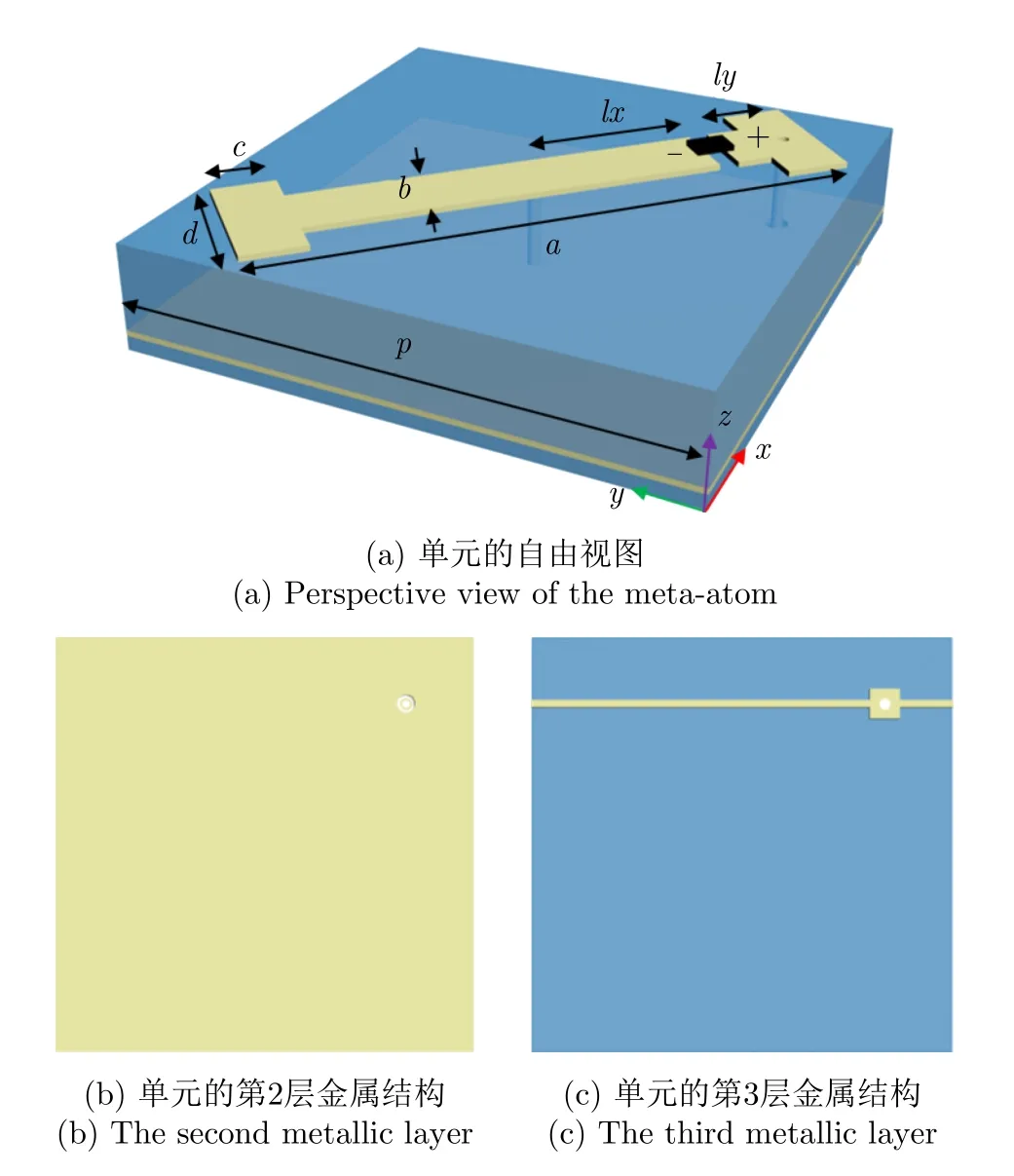
图2 转极化超构表面单元Fig.2 Schematic of the proposed polarization-converting meta-atom

图2为本文设计的用于幅度调制的转极化超构表面单元。该单元由三层金属结构和两层介质组成，其中金属结构由铜构成，而介质基板的介电常数为2.6，损耗角正切值为0.0035。上层金属结构为沿着对角线方向的“I”字图案，该图案被截断为两部分且由PIN二极管(Skyworks SMP1345-079LF)连接。中间层金属无结构图案且仅在其中挖去了一个圆形小孔，该层通过金属过孔与较长一侧“I”字图案相连。这层结构既作为金属底板，阻挡电磁波的透射，从而提高单元的反射幅度，也作为电极与外部直流驱动电压的负极相连。第3层金属结构为一个方形贴片与一根宽度为0.5 mm的偏置线，该偏置线将同列中的单元相连，从而实现列控偏置电路设计。该层结构通过金属过孔与较短一侧“I”字图案相连，且该过孔与第2层金属底板直流隔离。第3层结构作为电极与外部直流驱动电压的正极相连。通过参数优化设计，最终确定单元的周期为p=28 mm，其他结构参数为a=30 mm,b=3.6 mm,c=3.2 mm,d=7.2 mm,lx=8.7 mm和ly=3.1 mm。

我们利用CST Microwave Studio软件对该单元进行了全波电磁仿真分析，且单元的x方向和y方向均设置为周期边界条件，而z方向设置为open边界条件。全波仿真分析时，将入射波端口主极化方向设置为x极化，因此，同极化方向为x极化方向，而交叉极化为y极化方向。当驱动电路的电压分别为3.3 V和0 V时，开关二极管分别对应导通与截止两种工作状态。在实际仿真分析中，开关二极管的两种工作状态被等效为两种不同的电路模型，并与超构表面结构联合仿真。当二极管工作于“ON”状态时，可等效为电阻与电感的串联形式：R=1.5 Ω,L=0.7 nH；当二极管工作于“OFF”状态时，可等效为电容与电阻的串联形式：R=50 Ω,C=0.13 pF。该结构的同极化和交叉极化反射幅度/相位如图3所示。从全波仿真分析可知，超构表面单元的最佳工作频点为处于S频段的2.4 GHz，即设计在Wi-Fi的工作频段。电磁波正入射时，将开关二极管由截止状态切换至导通状态时，单元同极化方向的反射幅度由0.98下降至0.14，而交叉极化方向的反射幅度由0.08上升至0.85；同极化方向的反射相位在两种工作状态之间切换时几乎保持不变，而交叉极化方向的反射相位上升约80°。当入射波以20°以内的角度斜入射时，单元的同极化反射特性基本保持不变。因此，该单元具备良好的转极化特性，即在2.4 GHz处，开关二极管切换至导通状态时，大部分电磁波能量以交叉极化形式反射，此时同极化反射能量较小。相反地，当开关二极管切换至截止状态时，大部分电磁波能量以同极化形式反射，此时同极化反射能量较大。由于单元在两种状态之间切换时，同极化的反射系数具备较大的反射幅度差且可保持反射相位一致，我们将这两种反射系数用于幅度调制并分别定义为编码“0”和“1”。

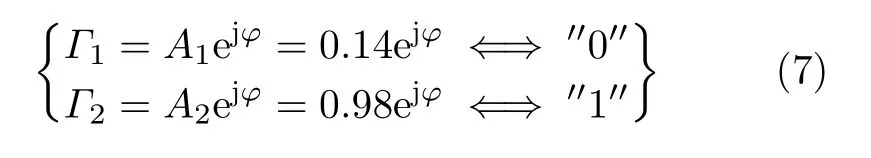
4 实验测试

基于以上全波仿真分析，我们利用标准印刷电路板(Standard Printed Circuit Board,PCB)工艺加工制作了超构表面样品。该样品包含10×10 个超构表面单元，整体尺寸为 280 mm×280 mm×3.5 mm，如图4(a)所示。测试环境如图4(b)所示。在实验测试与验证过程中，首先我们以方波调制信号为激励，验证时变编码电磁表面对基波与谐波的非线性调控；在此基础上，构建基于幅度调制的超构表面无线通信实验系统。

4.1 电磁波非线性调制

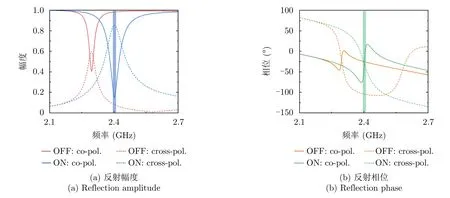
图3 转极化超构表面单元在开关二极管导通(ON)与截止(OFF)时同极化与交叉极化反射系数的全波仿真结果Fig.3 Full-wave simulated co-and cross-polarized results of meta-atom switching between“ON”state and“OFF”state

图4 加工样品与测试环境Fig.4 Photo of fabricated sample and experimental configuration

实验测试在标准微波暗室环境下进行。在实验中，一对带宽为1～18 GHz的宽带线极化喇叭天线分别作为发射端天线和接收端天线。其中，发射端天线与信号源相连，用于发射频率为2.4 GHz的单频正弦波信号，而接收端天线与频谱仪相连，用于接收并检测超构表面在时变调制下产生各频率分量及其能量大小。两个喇叭天线与超构表面距离均为2.5 m，天线因满足远场条件而保证了入射电磁波可被等效为平面波。任意波形发生器(Rigol DG992)用于提供特定频率的方波调制信号。

图5为超构表面在占空比为50%，频率分别为100 kHz,250 kHz,500 kHz的方波信号调制下的频谱分布特性，其中计算值根据全波仿真分析的反射系数理论计算得出。因绝大多数能量分布于前几阶谐波，为了便于观察，我们在图5中仅给出了–3阶至+3阶谐波的计算结果与测试结果，更高阶的谐波遵循同样的变化规律。结果表明，时变调制可将入射波能量由基波重新分配至基波和各谐波上，且调制信号的频率不影响频谱上各谐波能量大小，仅使各阶谐波的频率产生mf0偏移。例如，在100 kHz,250 kHz,500 kHz的方波信号调制下，+1阶谐波对应的频率分别为2.4001 GHz,2.40025 GHz,2.4005 GHz，其他各阶谐波可以此类推。所测得的各阶谐波能量均与同尺寸金属平板的反射能量对比，并进行归一化处理。基波能量的测试值略高于计算值，而所有奇数阶谐波能量的测试值略低于计算值，偶数阶谐波能量的理论值为0，而实际测试时也仅可测得非常微弱的反射幅度。总体而言，实验结果与测试结果吻合良好，一些少许误差主要是由于加工误差、建模误差等因素使超构表面的两种工作状态在同极化方向的反射幅度差略小于计算值造成的。

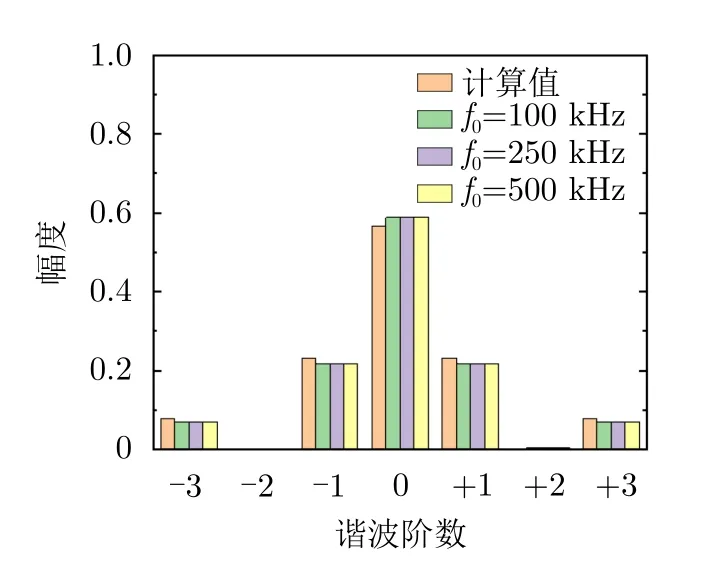
图5 超构表面在占空比为50%的不同频率的方波信号调制下各阶谐波反射幅度的计算值与测试值Fig.5 Calculated and measured spectral intensities under square-wave-type time-varying modulation with different modulation frequency but identical duty cycle S=50%

图6为超构表面在频率为500 kHz且占空比分别为25%,50%和75%的方波调制信号下，–3阶至+3阶谐波反射幅度的理论计算值与实验测试值。其中，计算值由全波仿真分析的反射系数计算得出，测试值经同尺寸金属板校准后作归一化处理。由于这3种时变调制信号的频率一致，因此各阶谐波对应频率偏移相同。根据前述的式(6)可知，基波的能量与占空比呈线性正相关关系，即方波的占空比越大，基波所分配的能量也越高；而谐波的能量以基波频率fc为轴呈对称分布，且各阶谐波之间呈非线性变化。如图6所示，测试结果与计算结果吻合良好，即测得的基波反射幅度随着方波信号占空比的增加而增加，谐波的反射幅度呈轴对称分布且与方波信号的占空比呈非线性相关。特别地，当占空比为50%时，偶数阶的能量为0。

4.2 无线通信实验

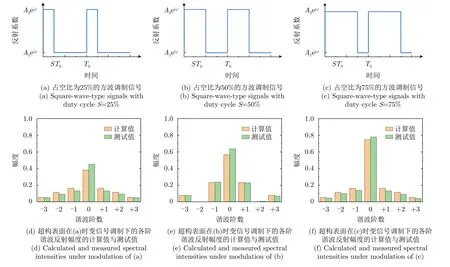
图6 超构表面在不同占空比、频率为500 kHz方波信号调制下的各阶谐波反射幅度的计算值与测试值Fig.6 Calculated and measured spectral intensities under square-wave-type time-varying modulation of 500 kHz with different duty cycle

与传统模拟调制相比，幅移键控(Amplitude-Shift Keying,ASK)、相移键控(Phase-Shift Keying,PSK)和频移键控(Frequency-Shift Keying,FSK)等数字调制方式更为高效、简单，因而广泛应用于现代无线通信系统。利用前文设计的转极化超构表面，我们构建了一种具有实际应用前景的二进制幅移键控(BASK)调制方式的新型无线通信系统，其系统组成及工作原理如图7(a)所示。BASK调制方式中“0”、“1”编码需对应两种相位相等、幅度相差较大的两种可切换的状态。在本系统中，“0”、“1”编码分别对应于超构表面单元在同极化反射的两种可切换状态，即分别对应于Γ1=0.14 ejφ,Γ2=0.98 ejφ，其中，每个码元携带1比特数字信息。在该系统中，发射端不需要复杂的电路系统进行调制信息处理，所需要传输的信息借助现场可编程门阵列(FPGA)以高低电平的方式直接调制至超构表面上，从而大幅度简化通信系统，有望进一步实现小型化、低成本通信。在实验验证中，信号源(Rohde&-Schwarz SMBV100A)作为发射源，通过线极化喇叭天线向超构表面发射频率为2.4 GHz的载波。另一个线极化喇叭天线用于接收频率为2.4 GHz的反射波信号，并将接收到的信号通过一台通用软件无线电外设(NI USRP-2974)解调后发送至终端设备。我们将需要传输的信息离散化为数据流，利用FPGA将离散后的数据流转化为控制信号并直接用于调制超构表面的工作状态，从而将所传输的信息调制至反射电磁波，即超构表面的同极化反射。若收、发天线间存在极化失配，此时接收天线将同时接收同极化与交叉极化的电磁波分量。假设收、发天线极化方向间夹角较小，当超构表面单元内PIN管截止时，交叉极化分量对测得反射系数的影响可忽略不计；当超构表面单元内PIN管导通时，交叉极化分量将令测得反射系数有所提高，从而导致两种工作状态对应的幅度差减少，可能导致解调信号时误码率提高。

为验证该无线通信系统的可行性，我们将一张2.04 KB (140像素×140像素)的黑白图片转化为由“0”和“1”编码组成的数据流，再将数据流以调制信号的方式，利用FPGA直接控制超构表面工作状态，经反射后调制于反射波上，并在接收端实时接收与解调信号，其中，数据流中的“0”、“1”编码按照所传输的黑白图片中黑色像素点、白色像素点的规律排列，若将调制信号的占空比定义为一个周期内高反射状态占调制信号的比例，那么占空比即为黑白图片中白色像素点所占据的比例。所发送的图片如图7(b)所示，传输码率为500 kbps时接收端所复原的图片如图7(c)所示。与发送的原图相比，接收端较好地解调出了发送信息，验证了无线通信系统的可靠性。同时，基带信号(基波信号)解调时对应的星座图如图7(d)所示，其中星座图中的点与原点距离为信号的相对幅度。从图中可知，“0”、“1”编码分别对应于星座图中原点附近的区域与离原点较远的区域，两个区域分离得较好且覆盖面积基本相等。两个区域中心与原点的连线基本处于同一直线，表明两个区域的相位基本一致。若继续提高传输码率至超过625 kbps时，由于每个PIN二极管的响应时间难以完全保持一致，可能导致时变极化编码表面的反射系数不稳定，即超构表面的反射系数难以在每个时刻均与式(7)相符，这将令星座图中的两个区域略有重叠，导致解调时的误码率提高。传输速率上限主要受有源器件响应速率和调制方式等因素限制，通过采用响应速度更快的元件(高速PIN二极管)和优化解调方式等可进一步提高传输速率上限。

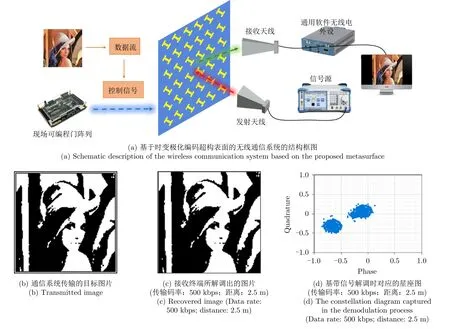
图7 无线通信系统Fig.7 The proposed wireless communication system

5 结论

本文基于时变极化编码超构表面实现了对基波和谐波的非线性调制，并通过调节方波调制信号的占空比进一步实现能量分布与频率频移调控。作为应用实例，提出了采用BASK调制方式的超构表面无线通信系统，该系统利用可调电磁表面的动态电磁响应特性，可将传输信息以数据流的形式直接调制至反射波被接收。实验结果均与理论分析计算结果吻合良好，且无线通信系统的最高传输速率达625 kbps。本文提出的非线性调制理论扩展了编码超构表面的研究范围，有望进一步应用于在MIMO通信、智能反射超构表面、全息成像等领域。此外，本文提出的调制方式可扩展至太赫兹和光波段，也可延伸至透射型时变编码超构表面。

社会治理是建立在多元主体共同参与基础之上的。在此过程中，只有不断激发各个参与主体的参与热情，社会治理才能达到预期的理想效果。就此而论，社会治理强调的是现代的多元主体参与，而不是传统意义上的自上而下的管理、命令或统治，其目的是要实现从“要我参与”到“我要参与”的转型和升级。在这一现代转型之中，不同主体要通过协商和对话，实现差异性偏好的理性转换，对社会治理中的重大问题形成各方均能接受的一致性意见，赢得各参与主体最大程度的理解、认同和支持。