海上风电柔性直流送出线路的纵联保护方法
2021-05-11杨林刚王霄鹤梅红明高玉青
刘 树,杨林刚,刘 斌,王霄鹤,梅红明,高玉青
(1.北京四方继保自动化股份有限公司,北京 100085;2.中国电建集团华东勘测设计研究院有限公司,杭州 311122)
实现传统化石能源的清洁化、推动可再生能源的规模化是我国经济和社会发展的一项重大任务[1-2]。风力发电是清洁能源中发展最成熟、商业应用最广泛的发电技术之一。目前,陆上风电待开发资源日益减少,近海风电由于环保、生态等因素,发展受到限制[3]。而深远海具有更广的范围和更丰富的风电资源,又不占据岸线和航道资源。因此,远距离海上风电是风电的发展趋势。
高压交流输电由于海底电缆的电容效应,不适用于远距离的海上风电并网[4]。而高压直流输电的输送距离更远,因此,采用直流输电技术已成为大容量远距离海上风电场并网的理想解决方案,尤其是模块化多电平柔性直流输电是目前研究的热点[5-6]。
不基于通信的单端量保护只利用局部信息即可识别直流故障,具有较高的判断速度。因此,单端量保护通常作为直流线路的主保护[7]。电流纵联保护是利用线路两端电流直接相加得到判据,在区外故障或稳态运行时,差动电流为穿越电流,不会引起保护动作;在区内故障时,线路两端保护流过的电流均为正方向,差动电流大于门槛值,差动保护动作[8]往往被作为直流输电线路的后备保护。
在柔直系统中,伪双极接线方式不需要设置专门的接地极,故海上风电柔直送出系统一般采用伪双极接线[9]。此外,海上风电直流送出通道为海底电缆,发生双极短路的概率很低。在伪双极系统发生单极接地故障时,换流器几乎不向故障点提供故障电流,在故障初期,故障电流主要由直流电缆分布电容产生[10-11]。当区外故障时,差动电流为被保护线路的电容电流,尤其是直流输电线路距离较长,分布式电容电流过大会导致差动电流过大,导致传统的电流纵联保护不能可靠地区分区内和区外故障。在故障稳态阶段,故障电流几乎为零,电流纵联保护仅仅依靠时间延时也不能可靠地判别区内故障。
针对上述问题,众多研究者提出了基于电容电流补偿的保护原理。文献[12]提出采用贝瑞隆模型与频变参数模型解决电流差动保护中电容电流的问题。文献[13]分析了长线路中分布电容对现有保护的影响,提出了一种电容电流补偿的直流差动保护方法。文献[14]提出了一种自适应时域补偿方法,提高了补偿精度和电流差动保护的灵敏度。文献[15]通过补偿线路两端保护接收故障信号时差的方法来进行电容电流的补偿,提高了直流差动保护的可靠性。文献[16-18]提出了基于线路精确模型的电容电流补偿方法。但是,目前上述电容电流补偿方法的时间窗仍然较长,在保护速动性和可靠性方面仍有所欠缺。
鉴于此,本文提出了一种适用于海上风电柔直送出线路的行波纵联保护方案。该方案基于行波原理,分别通过线路两端保护判断故障方向,再利用方向纵联区分内、外部故障。该方法不受暂态分布电容电流的影响,PSCAD仿真结果充分验证了所提方法的有效性和优越性。
1 海上风电柔直送出线路的保护难点
以图1所示的海上风电柔直送出系统的拓扑为例进行分析,两个海上风电场各接入一个柔性换流站,再分别经一回直流海底电缆线路送出,最终经过一个陆上换流站并入电网。
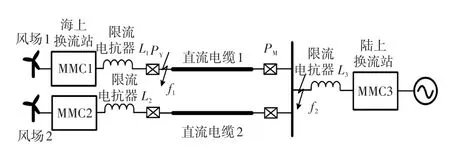
图1 海上风电柔直送出系统拓扑Fig.1 Topology of VSC-HVDC system for offshore wind farms
柔性直流的接线方式可分为真双极和伪双极接线两类。其中,伪双极接线方式不需要设置专门的接地极,故海上风电柔直送出系统一般采用伪双极接线。
1.1 伪双极直流系统单极接地故障分析
伪双极接地方式一般可分为直流侧接地和交流侧接地,如图2所示。图2(a)为在换流器出口直流两极线上并联接地大电阻,属于直流侧接地;图2(b)为换流变中性点经大电阻接地,图2(c)为阀侧交流接星型电感并串联大电阻接地,二者均属于交流侧接地[19]。当发生单极接地故障时,对于直流侧接地方式来说构不成放电回路,故障电流也就不存在;而对于交流侧接地方式,虽构成放电回路,但放电回路中均接入了大电阻,因此故障电流很小。
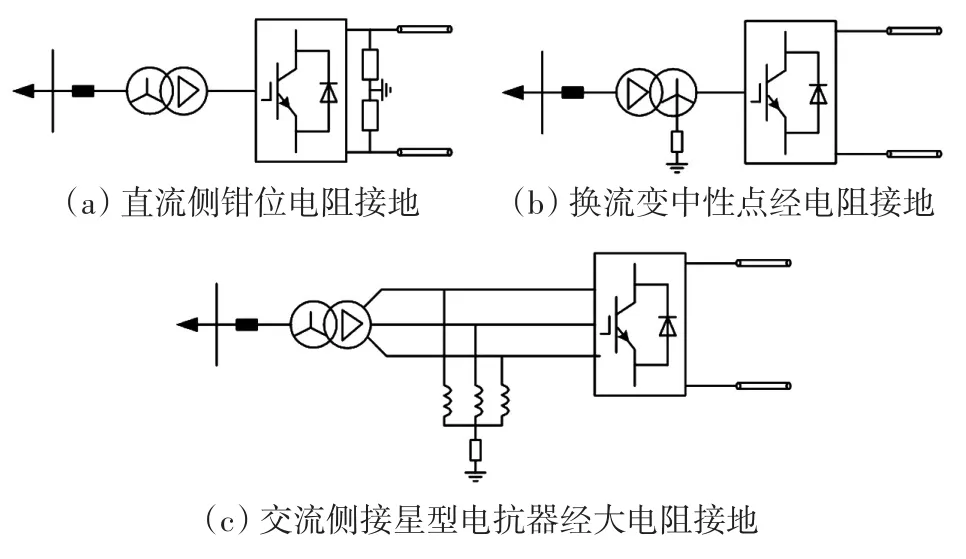
图2 典型的伪双极接线方式Fig.2 Typical connection modes of pseudo bipolar
本文以图2(b)中换流变阀侧中性点经电阻接地为例,分析伪双极系统中的单极接地故障特性。正极接地故障的示意图如图3(a)所示,其中Rl、Ll和C分别为直流正极线路的等值电阻、电感和电容,RN为换流变阀侧中性点接地电阻。故障发生初期的等值电路如图3(b)所示,故障线路电流仅由线路电容放电电流构成。线路电容的放电过程使电压下降,交流侧逐渐向直流侧馈流,如图3(c)所示。但由于换流变中性点大电阻RN的存在,交流侧馈流极其微小,近乎为零,可忽略不计。

图3 单极接地故障的等值电路Fig.3 Equivalent circuit under single-pole grounding fault
1.2 电流纵联保护在海上风电柔直送出线路的问题
理论上,直流线路处于正常运行及外部故障时,差动电流为穿越电流,直流线路纵联保护不会动作,只有在线路内部故障时保护才动作。但对于长距离直流电缆输电线路而言,在发生外部故障的暂态过程中,较大的分布电容电流的存在很有可能导致线路纵联保护误动作,对保护可靠性造成极大的影响。
以图1所示的海上风电柔直送出系统的拓扑为例进行分析,该柔直系统为伪双极系统且采用换流变阀侧星接中性点经大电阻接地方式。以正极接地故障为例,当直流电缆1发生区内正极接地故障时,等值电路图如图4(a)所示;当直流电缆1发生区外正极接地故障时,等值电路图如图4(b)所示。这里,等值电路仅考虑两回直流电缆的正极线路。
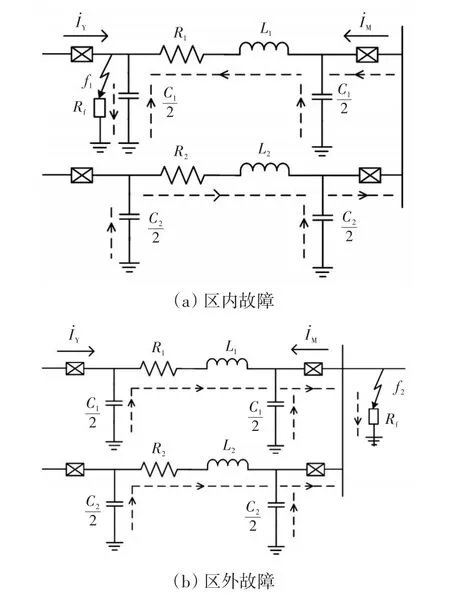
图4 单极接地故障等值电路Fig.4 Equivalent circuit under single-pole grounding fault
图4中,R1、L1和C1分别为直流电缆1正极线路的等值电阻、电感和电容,R2、L2和C2分别为直流电缆2正极线路的等值电阻、电感和电容。由于换流变阀侧中性点大电阻的影响,换流器向故障点溃流很小,几乎可以忽略。当发生区内故障时,从等值电路图4(a)可以看出,直流电缆1和2的正极线路同时向故障点放电。直流电缆1的电容放电电流不流经线路两端的保护,流经保护Y处的电流IY几乎为零,流经保护M处的电流IM为直流电缆2的电容电流,故直流电缆1处的差动电流为直流电缆2的电容放电电流,即相邻电缆线路的电容电流。
当发生区外故障时,从等值电路图4(b)可以看出,直流电缆1和2也同时向故障点放电。直流电缆2的电容放电电流不流经直流电缆1两端的保护,流过直流电缆1保护Y处的电流几乎为零,流过保护M处的电流为直流电缆1的电容放电电流,即本线路分布电容电流。因此,直流电缆1处的差动电流为本线路电缆电容电流。
综合上述分析可知,在故障初期,如果被保护线路与相邻线路的长度相似时,区内、外故障时的差动电流非常接近,尤其当区内发生经过渡电阻接地时,其差动电流远小于区外金属性故障,故电流纵联保护无法可靠区分区内故障和区外故障。在故障稳态阶段,由于换流变中性点大电阻的存在,故障电流几乎为零,电流纵联保护仅依靠时间延时也不能可靠地判别区内故障。因此,电流纵联保护不适用于海上风电伪双极柔直送出线路。
2 海上风电柔直送出线路纵联保护方法
2.1 直流输电线路的行波基本原理
输电线可假设由无数长度为dx的小段组成,设每单位长度的导线电感为L、电阻为r、对地电容为C、对地电导为g,则线路的分布参数模型如图5所示。

图5 线路的分布参数模型Fig.5 Distributed parameter model of transmission line
图5所示的线路模型满足关系式

为便于求解,将式(1)转换到频域内求解,对于直流输电线路,可表示为如下形式:
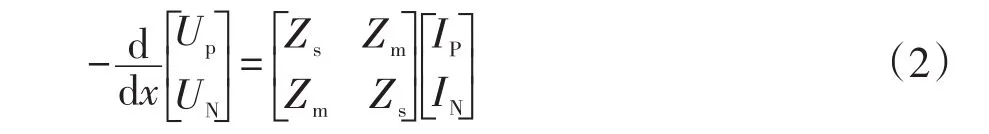

式中:Zs、Zm、Ys和Ym分别为线路的自阻抗、互阻抗、自导纳和互导纳;UP和IP分别为正极极线的电压和电流;UN和IN分别为负极极线的电压和电流。
设存在0模和1模分量满足如下关系:

式中:U0、I0、U1和I1分别为0模和1模的电压和电流分量;Q为特征向量矩阵。
对式(2)和式(3)分别进行求导,并把式(4)和式(5)代入到电压和电流的二阶微方程中可得

根据式(7)、(8)可得到行波的通解为
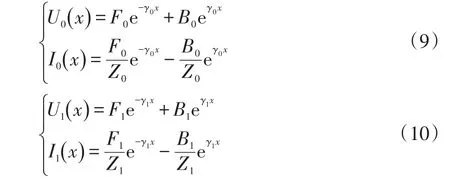
其中:

式中:Z0和γ0分别为0模的波阻抗和传播常数;Z1和γ1分别为1模的波阻抗和传播常数;F0、B0分别为电压0模分量的正向行波幅值和反向行波幅值;F1、B1分别为电压1模分量的正向行波幅值和反向行波幅值。式(9)、(10)中等号右侧第1项可认为是正向行波Δur,第2项可认为是反向行波Δue。
2.2 行波方向纵联保护的原理及判据
以如图6所示的三端柔性直流输电系统拓扑为例,分析行波方向纵联保护的原理,为便于说明,以下分析均以保护M为例。

图6 三端柔直输电系统示意Fig.6 Schematic of three-terminal VSC-HVDC transmission system
2.2.1 正方向故障
当保护M的正方向f1发生故障时,故障附加网络如图7(a)所示,故障行波传输过程如图7(b)所示。
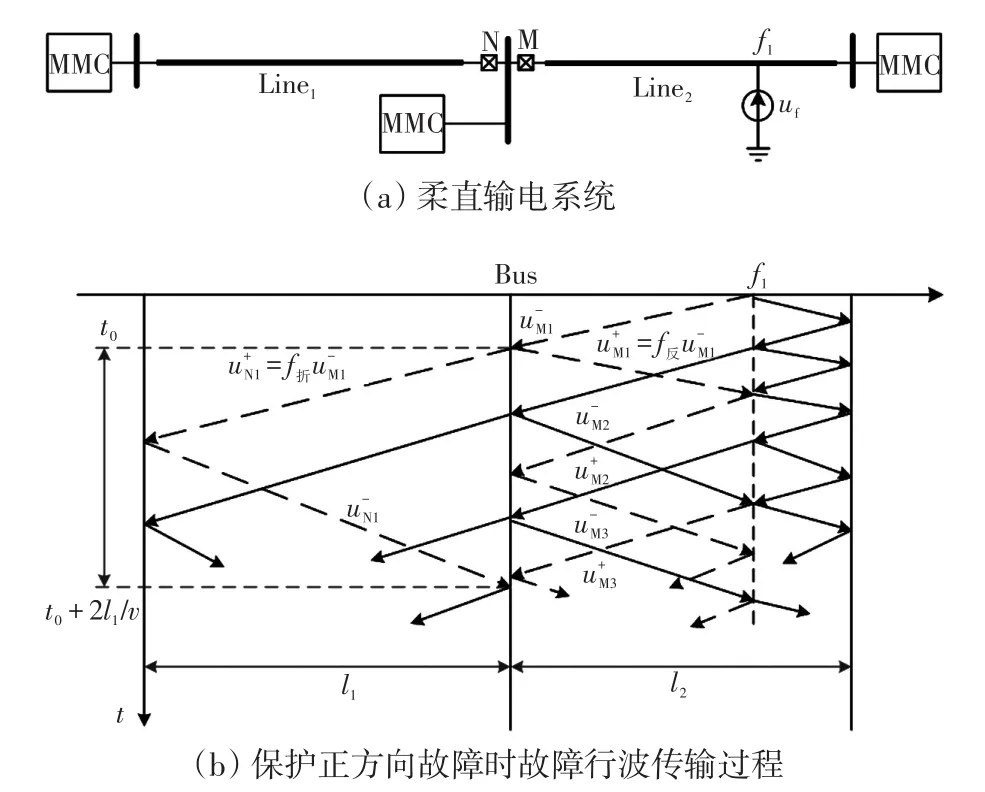
图7 正方向故障时行波传输特性Fig.7 Transmission characteristics of traveling wave under positive-direction fault
由上述分析可知,当保护正方向f1故障时,在t0~t0+2l1/v时间段内,保护M处的入射波与反射波之间均存在一个线路边界的反射系数,即测得的正向行波Δur和反向行波Δue之比可认为是行波在母线处的反射系数kr,如式(12)所示。

正向行波Δur和反向行波Δue的计算公式为

式中,r取0或1,分别代表0模和1模分量。
当保护正方向发生故障时,在故障行波经背侧线路末端反射达到本线路保护安装处的时间段内,正向行波与反向行波幅值比将小于1。
2.2.2 反方向故障
当保护M的反方向f2发生故障时,故障附加网络如图8(a)所示,故障行波传输过程如图8(b)所示。当故障行波到达保护M处,将发生折射和反射,其中,折射波将继续向保护所在的线路末端传播,并经线路末端反射至保护M处,令该时间段为t0~t0+2l2/v(t0为初始故障行波到达保护M处时刻,l2为保护M所在线路的长度)。在该时间段内,保护M处的故障行波主要包括:①经故障点反射的行波经本线路始端折射产生的折射波;②经过背侧线路末端反射的行波经本线路始端折射产生的折射波。
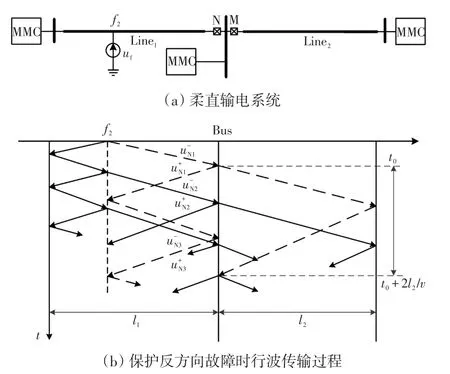
图8 反方向故障时行波传输特性Fig.8 Transmission characteristics of traveling wave under reverse-direction fault
上述分析可知,在t0~t0+2l2/v时间段内保护M处的电压和电流故障行波主要由上述两种行波构成,此时仅存在正向行波,反向行波未到达保护M处而为零。初始故障行波经线路始端发生折射形成正向行波,而在该正向行波经保护所在的线路末端反射至该保护处期间,反向行波接近于零。因此,此时正向行波与反向行波幅值比值将远远大于1。
因此,行波方向纵联保护可基于上述行波传输特征,利用正向行波和反向行波幅值比的方法判断故障方向。即故障启动后,若正向行波和反向行波幅值比小于整定值,则保护判为正方向故障,R取1;若正向行波和反向行波幅值比大于整定值kset(整定值kset一般选用略大于1的数,这里取2),则保护判为反方向故障,R取0,如式(14)所示。

线路两端的保护分别根据式(14)判断故障方向,并根据如式(15)所示的故障识别判据进行方向纵联,据此判别区、内外故障。

3 算例分析
基于PSCAD/EMTDC电磁暂态仿真平台搭建了如图9所示的海上风电柔直送出系统,该系统采用换流变阀侧星接中性点经大电阻接地的伪双极接线方式。两个海上风电场分别经过一回±250 kV直流海底电缆线路送出,线路长度均为50 km,由一个陆上换流站汇入电网。该系统主要参数如表1所示。直流电缆线路采用的是依频参数模型,两条电缆的线路参数是一致的,如表2所示。

图9 仿真算例拓扑Fig.9 Topology of simulation example

表1 仿真算例的主要参数Tab.1 Main parameters of simulation example

表2 直流电缆的主要参数Tab.2 Main parameters of DC cables
3.1电流纵联保护算法验证
如图9所示,故障f1对于保护PY来说为内部故障,f2为外部故障。为了验证电流纵联保护在伪双极系统中的可行性,令f1处金属性单极接地和f2处金属性单极接地,差动电流Idiff的仿真结果如图10(a)所示;令f1处经300 Ω过渡电阻单极接地和f2处金属性单极接地,差动电流Idiff的仿真结果如图10(b)所示,其中t=2 s为故障发生时刻。
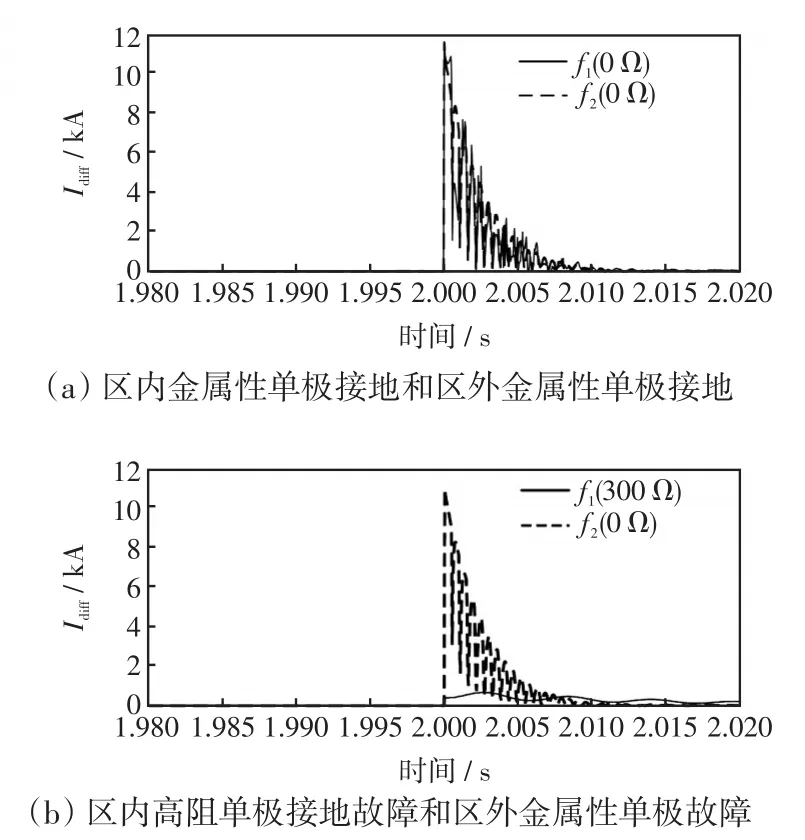
图10 电流纵联保护仿真结果Fig.10 Simulation results of current pilot protection
在伪双极系统中,发生单极接地故障后,换流器几乎不向故障点提供故障电流,故障电流主要由直流电缆分布电容产生。从图10(a)可以看出,当区内和区外分别发生金属性单极接地故障、被保护电缆的长度与相邻电缆的长度相似时,内部和外部故障条件下的差动电流是相似的。从图10(b)可以看出,当内部故障有过渡电阻时,差动电流远小于外部严重故障情况下的差动电流。
为了进一步验证电流纵联保护的可行性,对图9中不同位置处的单极接地进行了仿真,t=2 s为故障发生时刻,仿真结果如图11所示。

图11 不同位置故障下电流纵联保护的仿真结果Fig.11 Simulation results of current pilot protection at different fault positions
仿真结果表明在伪双极直流系统发生单极接地故障时,电流纵联保护不能可靠地区分内部和外部故障。
3.2行波方向纵联保护算法验证
为了验证本文提出的行波方向纵联保护算法的有效性,同样令f1处经300 Ω过渡电阻单极接地和f2处金属性单极接地,其中f1为区内故障,f2为区外故障,仿真结果分别如图12和图13所示。
图12为f1处经300 Ω过渡电阻单极接地时的线路两端正向行波、反向行波以及其幅值比,Y侧正向行波小于反向行波,其幅值比kY小于整定值2,则保护判为正方向故障,RY取1;M侧正向行波也小于反向行波,其幅值比kM也小于整定值2,则保护判为正方向故障,RM取1。线路两端保护分别进行了故障方向判断,接着根据式(15)进行方向纵联,由RYRM=1可判断出f1为区内故障。
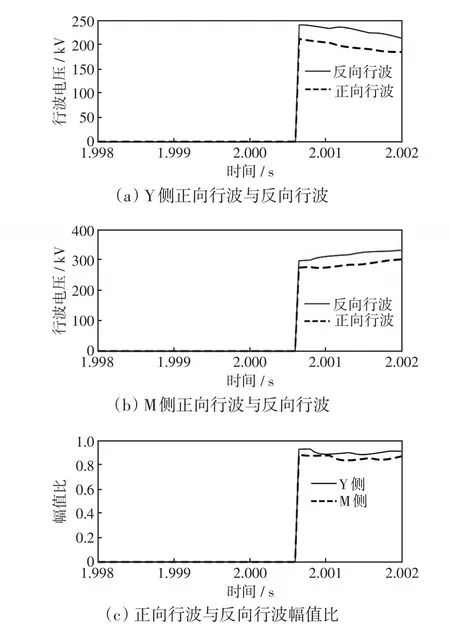
图12 区内故障仿真结果Fig.12 Simulation results under internal fault
图13为f2处金属性单极接地时的线路两端正向行波、反向行波以及其幅值比,Y侧正向行波小于反向行波,其幅值比kY为0.80,小于整定值2,则保护判为正方向故障,RY取1;M侧正向行波大于反向行波,其幅值比kM为24,远大于整定值2,则保护判为反方向故障,RM取0。线路两端保护分别进行了故障方向判断,接着根据式(15)进行方向纵联,由RYRM=0可判断出f2为区外故障。
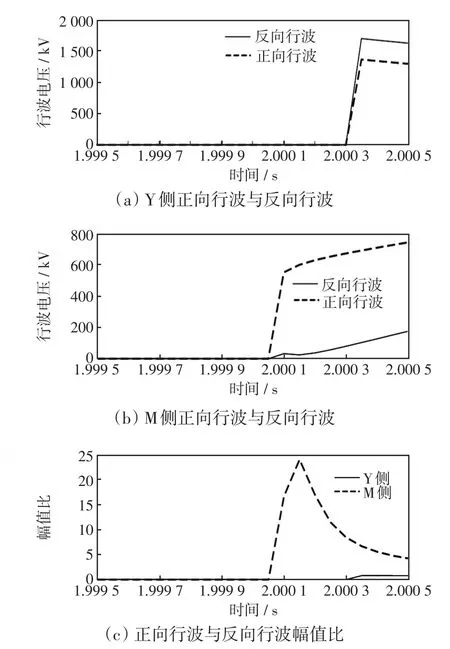
图13 区外故障仿真结果Fig.13 Simulation results under external fault
为了进一步验证本保护方案的可行性,在20 kHz采样率下,对不同位置处的故障进行了仿真,仿真结果如表3所示。

表3 行波方向纵联保护保护动作情况Tab.3 Performance of traveling wave directional pilot protection
从表3可以看出,无论是双极短路故障还是单极接地故障,本文提出的行波纵联保护方案均可以可靠地区分区内、外故障,不受线路分布电容影响,且具有较强的耐受过渡电阻能力。
4 结论
本文通过对海上风电柔性直流送出线路单极接地故障的分析,发现电流纵联保护不能可靠地区分区内和区外故障的问题,提出了海上风电柔性直流送出线路的行波方向纵联保护方法,所得结论如下:
(1)海上风电柔直送出系统常采用伪双极接线,当伪双极系统发生单极接地故障时,换流器几乎不向故障点提供故障电流。在故障初期,故障电流主要由故障极直流电缆分布电容产生,在故障稳态阶段,故障电流几乎为零;
(2)直流线路发生区内单极接地故障时,故障初期,差动电流近似等于相邻电缆的电容电流,尤其区内故障有过渡电阻时,差动电流远小于外部严重故障情况下的差动电流,电流纵联保护无法可靠区分区内故障和区外故障;故障稳态阶段,故障电流几乎为零,电流纵联保护仅仅依靠时间延时也不能可靠地判别区内故障;
(3)本文提出的行波纵联保护方案利用线路两端的行波方向保护分别进行故障方向判断,不受线路分布电容的影响,能可靠地区分区内、外故障。仿真验证也表明该原理能够快速、可靠地识别故障,具有较强的耐受过渡电阻能力。
