水冷型PEMFC温湿度建模与智能控制

陈 立,詹跃东

(昆明理工大学信息工程与自动化学院,云南 昆明 650504)

0 引言

质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)具有能量转化效率高、启动快和工作的温度低等优点，具有广泛的应用前景。燃料电池电化学反应的副产物是水和热。为了保证电池的长期稳定运行，必须不断地将水和热移除。电堆的温度对气体的压力、膜的含水量以及催化剂的活性等都会产生影响，直接影响着PEMFC的输出性能和使用寿命[1]。因此，将燃料电池的温湿度控制在最佳的状态至关重要。

本文基于温湿度耦合模型，建立电堆的电压模型以及热管理模型。根据不同的电流密度对应的最优温湿度不同[2]，通过对燃料电池的冷却水流量及进气加湿度进行综合控制，期望达到燃料电池工作的最佳温湿度，从而优化燃料电堆的输出性能以及延长电池的使用寿命。

1 PEMFC建模

1.1 燃料电池电压模型

电池的实际输出电压往往要低于开路电压ENernst。这是因为在电化学反应过程中会受到三种极化电压的影响，分别是活化损失电压Uact、欧姆损失电压Uohm和浓差损失电压Ucon[3]。PEMFC的单电池输出电压可以表示为：

Ust=ENernst-Uact-Uohm-Ucon

(1)

电池的开路电压ENernst可以由能斯特方程求得，可以表示为[4]:

(2)

式中：ΔG为吉布斯自由能；F为法拉第常数；ΔS为熵变；R为气体常数；PH2为氢气的有效分压；PO2为氧气的有效分压；Tstack为电池的工作温度、Tref为参考温度。

活化损失电压Uact可由经验模型给出[5]：

Uact=-[ξ1+ξ2T+ξ3Tln(CO2)+ξ4Tln(i)]

(3)

式中：ε为由试验数据拟合得到的经验系数。

欧姆损失电压Uohm是由质子膜的等效膜阻抗RM和阻碍质子通过膜的阻抗RC产生的电压降:

Uohm=IRohm=I(RM+RC)

(4)

欧姆内阻Rohm可由式(5)表示：

(5)

式中:tm为质子膜的厚度；λ为质子膜的含水量。

(6)

电堆在高电流密度运行时，反应物的浓度会下降，这时就会产生浓差损失电压，Ucon可以表示为：

(7)

式中:B为由电池本身结构决定的常数；i为电流密度，imax为最大电流密度。

由式(1)～式(7)可知，电堆的输出电压主要受电池的工作温湿度影响，可以表示为:

Ucell=f(Tstack,RHstack,i)

(8)

1.2 温湿度耦合模型

燃料电池系统是一个多输入、多输出、强耦合的复杂系统，但是在温湿度的耦合关系中存在温度对湿度影响大、湿度对温度影响小的特点[6]。因此，可以通过研究PEMFC的水管理模型实现对温湿度解耦。

通过研究电堆内部含水量的变化，可以得到水冷型PEMFC的膜含水量数学模型，如式(9)所示：

(9)

式中:Wstack为电堆的膜含水量；Wg为电化学反应生成的水量；WH2、WO2分别为H2、O2的含水量；Wouta、Woutc分别为阳极和阴极的尾气排放含水量。

根据文献[2]，可以得到电堆膜相对湿度模型:

(10)

式中:ζ1～7为可变参数，取值受到控制变量的影响。

计算模型为：

(11)

式中:饱和蒸气压Psat只与电堆的温度Tstack有关。

其表达式为：

(12)

膜相对含水量模型的相关参数符号说明如表1所示。在进行仿真时，将Pair和PH2这些可控变量均设为定值。由式(10)可以看出，电池的相对湿度与电堆的温度和电流密切相关，将式(8)中的膜的含水量RHstack用耦合模型替代，可以得到基于温湿度耦合的电堆电压模型。

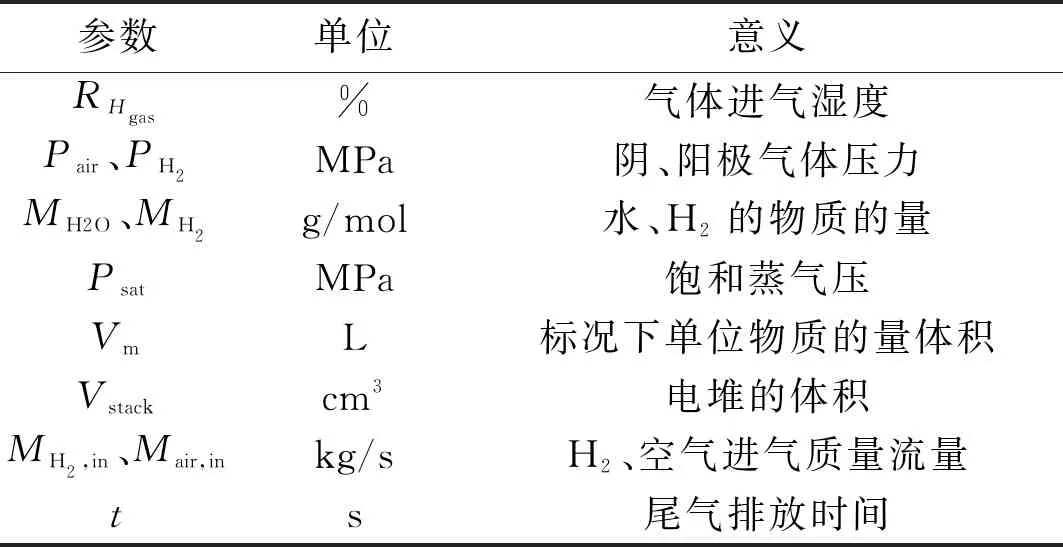
表1 相关参数符号说明

1.3 PEMFC温度动态模型

假设如下：忽略系统的热辐射和管道的散热；每个子系统的冷却水温度是均匀的；参与反应的气体处于理想状态下[7]。

根据能量守恒定律Q=CMΔT，可以得到燃料电池热平衡方程如下：

(13)

式中:Mst为电堆的质量；Cst为电堆的比热容。

电化学的全部化学能Qtot可以表示为：

(14)

式中:ΔH为氢气的燃烧焓;N为单电池个数;Ist为电堆的工作电流;F为法拉第常数。

电堆的输出功率Pst是电池电压Ust和Ist的乘积，Ust由上面的电压模型得到。

Pst=NUst×Ist

(15)

冷却水的散热功率可以表示为：

Qcl=WclCP,H2O(Tst-Tst_in)

(16)

式中:Wcl为冷却水的流量;CP,H2O为水的比热容;Tst_in为冷却水的入口温度;Tst为冷却水出口温度，

由于电堆比热容较大，将Tst近似为电堆的工作温度。水冷型PEMFC约90%的热量都是由冷却水排出的，故此模型忽略Qgas和Qamb[8]。

1.4 最优温湿度操作条件建模

由文献[2]的仿真试验研究对最佳温湿度与电流密度特性分析，得到的不同的电流密度匹配的最优温湿度函数模型如下：

T优=algi+b+mexp(ni)

(18)

RH优=α1i4+α2i3+α3i2+α4i+α5

(19)

式中:T优、RH优为不同电流密度对应的最佳温湿度；a、b、m、n和α1～5为温湿度特性模型参数。

由式(18)、式(19)可以看到，电池的最优温湿度只与电流有关，每个电流密度对应不同的最佳温湿度。对燃料电池最优输出性能的控制就是对电堆的最优温湿度进行控制。只要将电池控制在每个电流密度对应的最优温湿度下，就可以得到最优的输出电压，实现对燃料电池输出性能的最优控制[9]。本文把冷却水的流量以及气体的加湿度作为被控对象，使得PEMFC的工作温湿度始终保持在最优的状态。这样不仅可以保证输出性能保持最优，也可以避免因温湿度变化太大而导致质子膜的失效。

2 PEMFC温湿度控制器的设计

反向传播(back propagation,BP)神经网络比例积分微分(proportional integral differential，PID)原理如图1所示。

图1 BP神经网络PID原理图

燃料电池在实际运行时，负载的变化过快会加快质子膜的失效并影响其输出性能和寿命[10]。因此，在负载变化时燃料电池系统的最优温湿度能够快速响应并跟随电流变化是保持输出最优性能的关键。本研究采用变论域模糊PID和BP神经网络控制器对温湿度进行综合控制。基于变论域模糊PID控制器的设计在我的已投稿的论文中已作详细的说明[11]。由于篇幅原因，本文重点阐述BP神经网络控制器的设计。

2.1 BP神经网络控制器的结构设计

PID控制器虽然算法简单，但是鲁棒性、稳定性较好以及学习能力强。BP神经网络是按照误差逆向传播算法训练的多层前馈神经网络[12]，具有较强的自组织、自学习和自适应的能力[13]。BP神经网络控制器是由PID和BP神经网络两部分组成，其结构如图1所示。传统的PID控制器是对被控对象进行直接的闭环控制，BP神经网络对其三个参数Kp、Ki和Kd在线调整。由此，可以得到PID的控制算法如下：

u(k)=u(k-1)+kp[e(k)-e(k-1)]+kie(k)+kd[e(k)-2e(k-1)+e(k-2)]

(20)

式中:e(k)=r(k)-y(k),表示k时刻的偏差。

对于PID的三个可调参数Kp、Ki和Kd，通过神经网络的自学习调整加权系数，神经网络的输出对应于最优的PID控制参数。

2.2 BP神经网络控制器算法

BP神经网络包含三个部分，分别是输入层i、隐含层j和输出层l，其结构如图2所示。其中，输入层的神经元数i=3,隐含层神经元数j=6，输出层神经元数l=3。下文中0、1和2分别表示输入层、隐含层和输出层。由于Kp、Ki和Kd不能为负值，所以输出层的激活函数选用非负的Sigmoid函数，而隐含层的神经元可取正负对称的Sigmoid激活函数[14]。

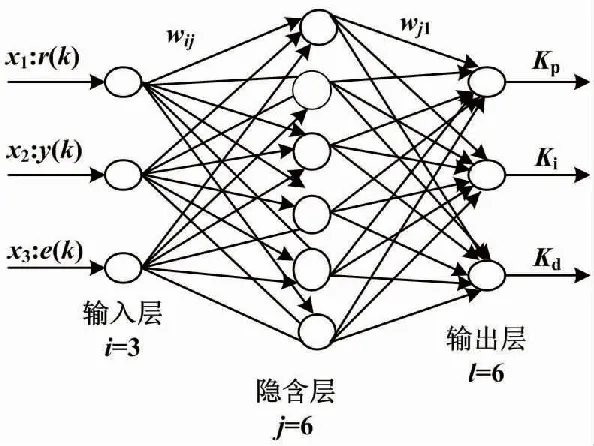
图2 BP神经网络结构图

由图2可知，神经网络输入层的输入、输出为：

(21)

式中:x1(k)=r(k)为系统的目标输出；x2(k)=y(k)为系统的实际输出；x3(k)=e(k)为偏差。

隐含层的输入、输出为：

(22)

输出层的输入、输出为：

(23)

采用误差的二次方作为性能指标函数[15]：

(24)

(25)

由式(23)可得：

(26)

因此，将式(29)代入式(28)，可以得到输出层的学习算法:

(27)

同理可得隐含层的学习算法：

(28)

3 仿真结果及分析

在仿真模型中，单电池数N=120，活化面积A=100 cm2，膜的厚度tm=178 μm。在仿真试验中，将电流变化作为扰动输入，选择阶跃变化作为测试信号，如图3所示。

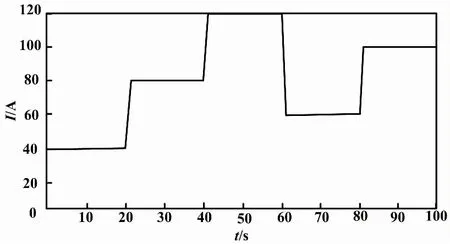
图3 电流阶跃变化曲线图

3.1 最优温湿度控制策略

由式(18)和式(19)可以得到每个电流密度对应的一组最优温湿度，将最优的温湿度作为设定值。基于温湿度的耦合的电压模型，通过所设计的变论域模糊PID和BP神经网络控制器对冷却水流量和进气气体加湿度加以综合控制，可以保持电堆的最优输出性能。电流变化对应的最优温度和湿度的响应曲线如图4所示。由图4可知，所设计的控制器能够很好地响应最优温湿度的变化且稳态误差均比较符合要求。

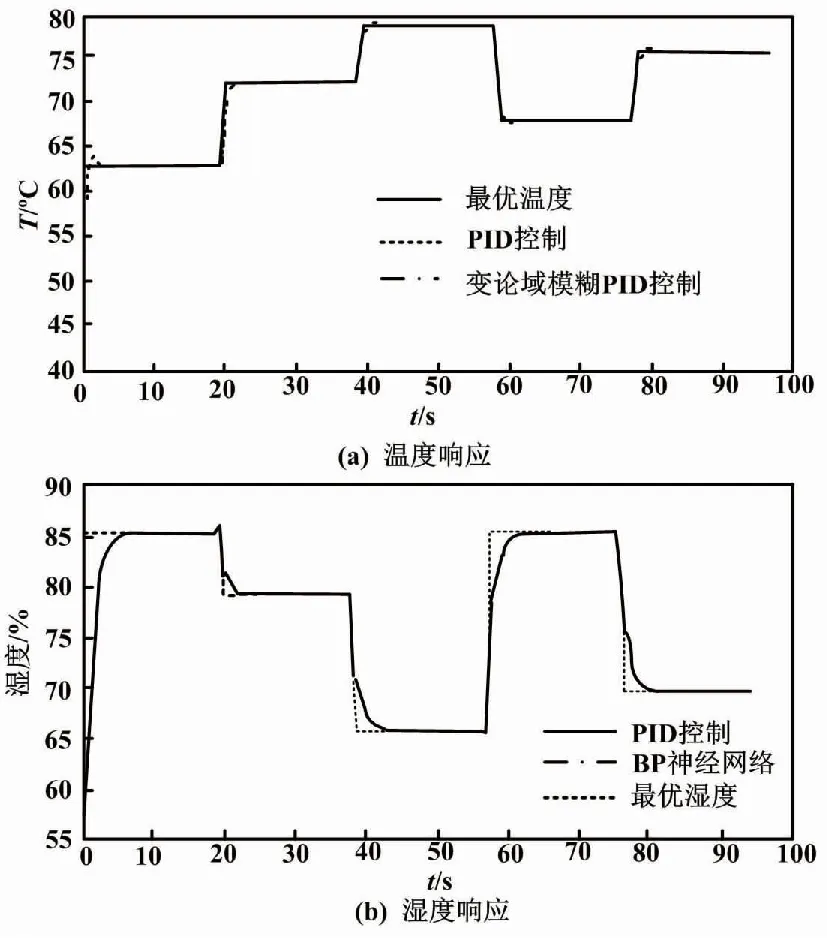
图4 不同控制器下的最优温湿度响应曲线

在仿真试验中，对散热器的空气流量进行控制，将冷却水的入口温度保持在60 ℃(即Tst_in=333 K),环境温度Tatm=298 K。以跟随电流变化的最优温度与电堆的实际工作温度的差值为偏差e(k)和偏差变化率(k)作为变论域模糊PID控制器的输入，输出为被控对象冷却水流量。在负载扰动下，冷却水流量如图5所示，得到跟随电流变化的最优温度曲线如图6所示。

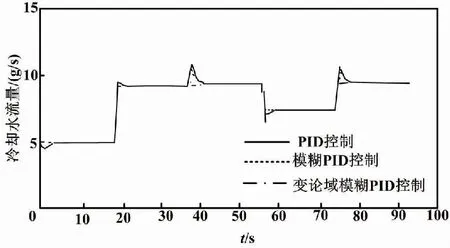
图5 电流变化下的冷却水流量

图6 跟随电流变化的最优温度曲线

通过对图6分析可知，所设计的控制器能够快速跟随电流的变化，始终把温度保持在最优范围。与另外两种控制器相比，本文设计的控制器可以明显降低系统超调而且响应速度更快。

通过BP神经网络控制器对进气气体的加湿度进行控制。其中，跟随电流变化的最优湿度为r(k)、电堆运行时的膜的相对湿度为y(k)和偏差e(k)作为BP神经网络控制器的输入，输出为进气体加湿度。进气电流变化下气体加湿度曲线如图7所示。跟随电流变化下的最优湿度曲线如图8所示。由图7和图8可以看到，BP神经网络控制器响应速度非常快，相对于PID和模糊PID控制器，其响应速度可以提高8～10 s，且控制精度明显更好。

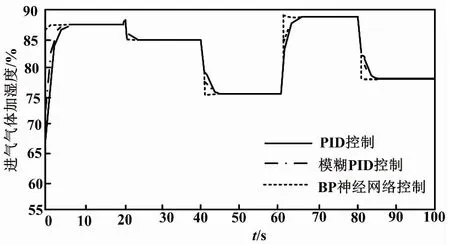
图7 电流变化下进气气体加湿度曲线

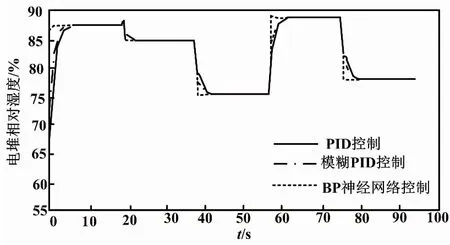
图8 跟随电流变化的最优湿度曲线

3.2 PEMFC最优输出电压

根据式(8)，在负载电流一定的条件下，输出电压只与电池的温度和湿度有关。所以对于电池的最优输出电压的控制就是对PEMFC的最优温湿度进行控制。因此，只要将电池的温湿度控制在最优就可以得到最佳的输出性能。在负载电流变化后，电池电压可以迅速响应，实现了对PEMFC的最优控制。PEMFC最优电压响应曲线如图9所示。

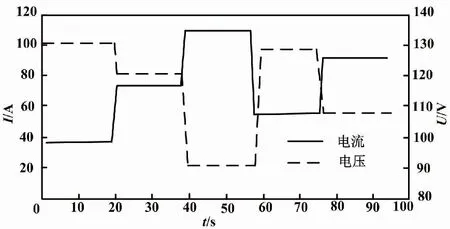
图9 PEMFC最优电压响应曲线

4 结论

基于温湿度耦合模型，建立最优温湿度操作条件的电堆电压和热管理模型。PEMFC的输出电压是电池温度、湿度和电流的函数，电池的温湿度是影响输出性能的主要因素。根据仿真对比试验结果，所建立的温湿度模型能够有效降低温湿度之间的耦合作用，所设计的温湿度控制器可以明显减少进气气体湿度以及电堆出口冷却水温度的调节时间和超调量。通过对冷却水流量和进气气体加湿度的综合控制，可以使电堆的工作温湿度保持在最佳状态，从而保证输出性能最优，提高输出功率。