气体超声波流量计整流装置设计与仿真分析

章圣意，姚海滨，董双双，李国占，张洪军

(1.浙江苍南仪表集团股份有限公司，浙江 苍南 325802；2.中国计量大学计量测试工程学院，浙江 杭州 310018)

0 引言

超声波流量计因具有无接触、无压损等优点而广泛应用于诸多领域，但其测量精度易受管内流动状态的影响[1]。实际应用现场的扰流件会导致管内出现流态畸变现象，且往往无足够的长直管段供流动缓慢恢复至理想测量条件[2]。

目前，通常在流量计上游加装整流装置以减少流态畸变对其测量精度的影响[3-4]。常用的整流装置有三类。第一类是采用管束式结构将流体分割为若干细小流束以消除二次流和涡流[5]；第二类是采用多孔板式结构以产生轴对称的速度分布[6-8]；学者们尝试将第一和第二类整流装置相结合以实现更好的整流效果，于是就出现了第三类整流装置[9]。

本文设计了一款第三类整流装置，运用大涡模拟方法研究该整流装置对流量计内部畸变流场的整流机理，评估其对流量计测量精度的改善效果。

1 超声波流量计整流装置结构

本文研究对象为一款DN50超声波流量计整流结构。为了使气体超声波流量计结构更加紧凑，对整流装置和超声波流量测量段进行了一体化设计。流量计测量流道由整流和超声波流量测量两部分组成。流体进入流量计流道时，首先经整流装置进行整直，纠正流动偏斜和畸变，然后进入超声波流量测量段。当流量计上游存在弯管、阀门等阻流件时，管内会出现二次流造成轴向漩涡，以及流速分布偏斜、严重偏离充分发展速度分布等情况。在设计整流装置时，可从消除和减弱大涡结构和纠正流动偏斜、畸形两个方面考虑。在纠正流动偏斜、畸形方面，一般可采用多孔孔板或叶片起旋器，而后者能力更强；在消除漩涡流动，纠正流动方向方面，蜂窝整直器是比较通行的选择。本文设计中采用了起旋器+蜂窝整直器的方案。为了使流体流经起旋器后能有一定的自我修复空间，该方案在起旋器和蜂窝整直器之间留有一定距离。超声波流量计整流装置示意图如图1所示。

图1 超声波流量计整流装置示意图

起旋器和蜂窝整直器结构如图2所示。

图2 起旋器和蜂窝整直器结构图

起旋器含有10个风扇式叶片，叶片厚度为0.8 mm，轴向长度为12 mm，叶片的流向倾角沿径向逐渐增大，轮毂向上游延伸进行光滑过渡。轮毂直径为10 mm，向上游延伸10 mm进行光滑过度以减少流动分离。蜂窝整直器的蜂窝外接圆直径为5 mm，蜂窝器轴向长度为30 mm，起旋器叶片尾缘与蜂窝器前缘之间的距离为38 mm。起旋器与蜂窝整直器之间的直管段构成的混合腔整流器的总长度为90 mm。

2 物理模型与数值方法

为了检验整流装置的效果，在超声波流量计上游设置扰流件，管道内径d=50 mm，流动为双弯头+半开平板的严重扰流条件。采用计算流体力学方法，针对这一管道模型进行了仿真研究。其中，扰流件与超声波流量计的流量范围为1～160 m3/h。扰流流动管路模型如图3所示。

图3 扰流流动管路模型

基于Ansys ICEM软件，采用模块化策略，分别对管道、起旋器和蜂窝器各部分流体域进行网格划分。其中：管道与起旋器采用结构化网格、而蜂窝器则采用非结构化网格，且对壁面附近网格进行加密处理，网格总数约为500万。计算域网格如图4所示。

图4 计算域网格

基于商业软件Ansys Fluent，采用大涡模拟方法对流量计内部流动进行仿真分析，管道入口边界设为质量流量入口条件，管道出口边界设为压力出口条件，静压为大气压，整流装置与管道壁面均设为绝热无滑移壁面。大涡模拟的亚格子模型选取WMLES模型[10]，压力与速度耦合方程的求解采用Simple方法，各物理量应用二阶迎风格式，最大流量时的时间步长为1×10-5s，待流场达到准稳态后对数据进行平均以获得时均量。

3 结果与讨论

3.1 无/有整流装置时流场对比分析

扰流件引起流动漩涡和流速分布畸形，对下游很长一段距离内流动分布产生影响，作为一个典型工况，Qmax时流量计内横截面上的速度云图如图5所示。由图5(a)可见，由于扰流件的存在，横截面内流速分布发生严重畸变，中心区域不再是流速较大区域，流速分布也不再是中间对称。由图5(b)可知，由于起旋器和蜂窝整直器的作用，使得管内流速分布重新趋于中心对称，更接近充分发展状态。

图5 Qmax时流量计内横截面上的速度云图

超声波流量计声道上的瞬时速度分布如图6所示。由图6可知，对于无整流装置情况，声道上流速分布出现严重偏斜和剧烈波动，且其波动幅值随着流量的增加而增大。这显然是由于扰流件造成流道内存在强烈的旋涡与二次流的影响；安装整流装置之后，不仅效减弱了流量计内部的流速分布偏斜和波动等流动畸变，而且流速分布更为均匀和对称，更加接近与充分发展状态。这对于超声波流量计测量精度的保证是非常重要的。

表1给出了无/有扰流时超声流量计声道上的平均速度的比值，该比值越接近于1，说明扰流影响越小，测量越准确。由表1数据可见，对于无整流装置的情况，相同流量条件下无/有扰流时超声波流量计声道上的平均速度存在较大差异，扰流件引起的流态畸变可能会造成测量误差最高可达20%左右。对于有整流装置情况，整流器极大限度地减少了流态畸变，相同流量条件下无/有扰流时超声流量计声道的平均速度较为接近，偏差均在2.0%以内，显著减少了管内流态畸变对超声波流量计测量精度的负面影响。

图6 超声波流量计声道上的瞬时速度分布

表1 无/有扰流时超声流量计声道上平均速度的比值

3.2 扰流件距离的影响

扰流件下游流动自身会逐渐恢复，距离越远其影响会越小，研究流量计与扰流件的距离影响，以便明确整流装置的安装要求。为此，对比了距离L=3d、5d、7d和10d这4种工况的流场情况。

图7和图8给出了2种流量情况下，不同安装距离时超声流量计流量测量段x-y和x-z平面内声道上的时均速度分布。由图7(a)和图8(a)可见，在4种距离情况下x-y平面内流速分布相对都比较对称；x-z平面内流速分布，当距离为3d时还存在较严重偏斜，当整流装置与扰流件距离在5倍管径以上时，管内流态畸变已经能够得到较好纠正，安装整流装置后，超声波流量计上游直管段可要求为5倍管径。此外，x-y平面内流速分布更加对称和均匀。即，当超声波流量计换能器声道与弯头(本研究中与其靠近的弯头)在同一平面内时测量误差相对较小。

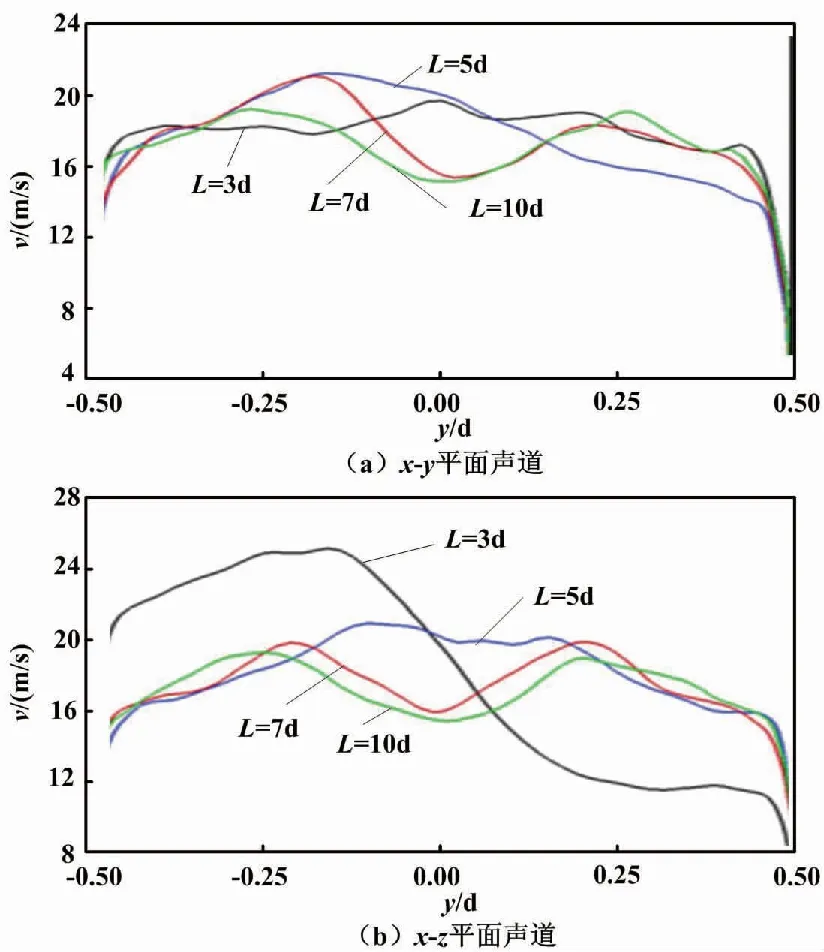
图7 0.75Qmax时超声流量计不同声道上的时均流向速度分布

图8 0.1Qmax时超声流量计不同声道上的时均流向速度分布

表2给出了超声波流量计x-y和x-z平面声道上时均速度的均值。

由表2数据可见，随着整流装置与扰流件的距离增大，x-y和x-z平面声道上速度均值的差值随之减小，表明流量计内部的速度分布趋于均匀。此外，当间距大于5倍管径时继续增大间距，两声道上速度均值的差值无明显减小，表明整流装置与扰流件的安装间距满足要求后继续增大间距所带来的有利影响有限，反映出本文所设计的整流装置具有良好的整流效果。

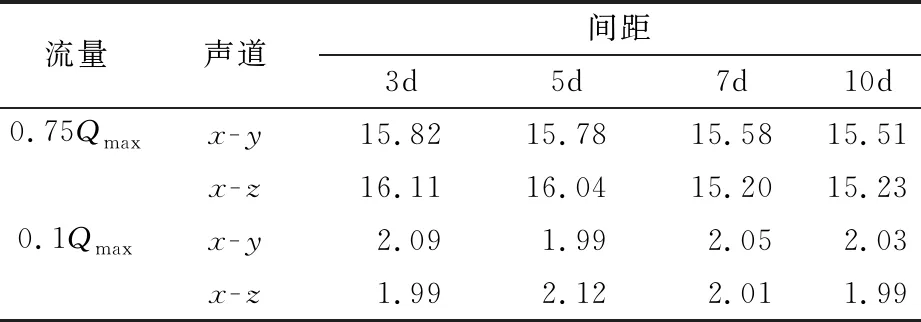
表2 超声流量计x-y和x-z平面声道上时均流向速度的均值

4 结论

本文采用大涡模拟方法对超声波流量计内部的流场进行仿真，分析了所设计的复合整流装置对流量计内部畸变流场的整流效果。主要结论如下。

①整流装置采用起旋器与蜂窝整直器组合的整流装置设计方案，结构紧凑，DN50的整流装置长度只有90 mm。

②采用流体力学数值模拟方法对整流装置效果进行了仿真分析。在双弯头+半开平板的严重扰流条件下，未加装整流装置时，位于扰流件下游5d的流量计流速分布仍出现严重偏斜和畸变，声道上平均流速与真实流速偏差达20%；有整流装置时，声道上流速均值偏差2.0%以内，整流效果明显。

③加装整流装置后，上游扰流件距离超过5倍管径时流速分布即可满足超声流量计测量需要，缩短了流量计对上游直管段的长度要求。