基于Hyperworks的大直径盾构拖车分析研究

孙秀洁，吴嘉宜，贾 甜，谷俊峰，阮诗伦，▲

(1.大连理工大学重大装备设计与制造郑州研究院，河南郑州450002；2.中铁工程装备集团有限公司，河南郑州450002；3.大连理工大学运载工程与力学学部，辽宁大连116024)

0 引言

世界盾构技术正朝着超大断面化、异形断面化、超大深度化、超长距离化的方向发展，世界盾构技术的超大断面化，使得大直径泥水盾构的应用成为一种发展趋势，且大直径泥水盾构对于开发我国沿江、沿海、沿河及许多城市的经济发展具有十分重要的战略意义[1-2]。因此，抓紧和加快大直径泥水盾构技术的研究，进而掌握大直径泥水盾构的设计、制造和施工技术能极大地提高市场竞争力，是我国与国际先进盾构技术接轨的重要步骤。

大直径盾构技术的发展对盾构结构的综合性能提出了更高、更严苛的要求。目前国内已出现15 m级的大直径盾构，但是大直径盾构的整机重量可达到1000 t以上，不仅原料成本高，而且转运安装困难，时间周期长[3]。盾构机的后配套装置一般由一节连接桥和若干拖车组成，拖车是盾构机掘进不可缺少的一部分，是用于承载盾构机掘进的主要设备，在大直径盾构中，一节拖车重量高达几百吨，拖车的轻量化设计可以有效解决设计浪费和成本失控，具有重要的经济和技术意义。

轻量化设计受到越来越广泛的关注，成为工程机械设计制造产业发展的重要趋势之一。

轻量化是在满足规范要求、保证结构安全和产品品质的前提下，通过合理的结构布置、科学的计算论证、适度的构造措施，充分发挥材料性能、合理节约造价的设计方法[4]。轻量化设计可以帮助工程师们加深对结构理解、激发灵感，带来全新的设计和方案，实现仅凭直觉无法达到的设计改进。

1 拖车的静力学分析

静力分析主要用于研究结构在恒定载荷作用下的响应，如结构的位移、应力、应变，通过结构响应校核结构强度。静力分析中不考虑随时间变化的载荷，忽略惯性力和阻尼[5]。由于拖车为准匀速运动，根据拖车的静力分析结果，可以确定拖车结构中的危险区域，为拖车的优化设计提供参考。

1.1 拖车有限元模型建立

本文以某型号大直径盾构机一号拖车为研究对象，拖车主体由板件和标准H型钢焊接构成，型钢长度与横截面的比率超过10，且横截面始终保持不变，可简化为梁模型[6]。其余板件简化为壳体，忽略对计算影响不大的特征。如图1所示，一号拖车有限元模型简化为梁-壳模型，整车计算中，壳与梁、梁与梁的连接采用刚节点连接，其中壳单元划分尽量采用四边形板壳单元模拟，并以少量三角形单元作为过渡，一号拖车的材料参数如表1所示。

表1 拖车材料参数

图1 拖车有限元模型

1.2 拖车的荷载及约束

在拖车上施加的载荷既要符合实际工况且要反映拖车的极限受力情况。根据试验段检测数据对拖车施加载荷及约束。

拖车的极限工作情况下荷载：

1)所承载设备的重力：将拖车所承载的所有设备的重力加载至实际承载面，如图2所示；

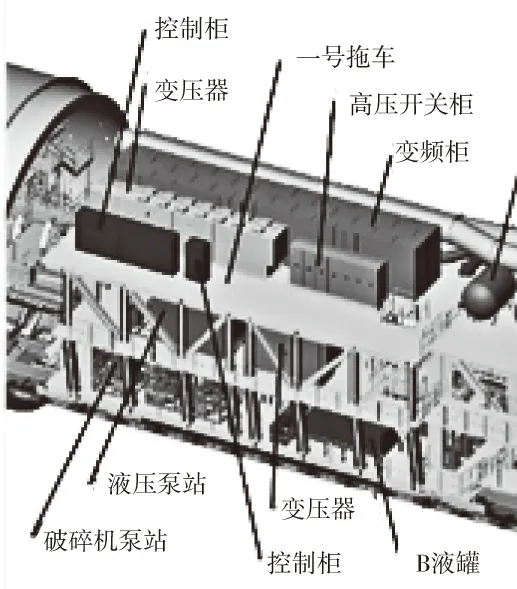
图2 拖车设备负载图

2)连接桥作用力：连接桥搭接在两个拖车中间，将连接桥的重量加载至分析对象，加载位置为连接桥搭接面；

3)前部设备拖拽力：拖拽力的大小为所拖拽设备重力乘以相应摩擦系数；

4)拖车自重。

拖车的极限工作情况下约束：底部轮对简支约束。

1.3 结果分析与讨论

在极限工况下，应力较大的区域集中于梁单元交界处，而且靠近壳单元的梁的连接处应力最大，这些位置都是刚度变化较大的部位，制造过程中应该特别关注这些位置，对于应力较大的关键部位焊接处要提高精度[7]。

拖车的最大等效应力为160.28 MPa，小于Q355B钢的屈服极限355 MPa，拖车的安全系数为2.21，大于推荐系数2，最大变形小于30.48 mm，即拖车跨度的1/800，所以拖车的强度和刚度满足要求。

拖车整体应力分布不均匀，应力较大部位集中在特定区域，大部分区域应力较小，造成材料浪费，有必要开展轻量化设计。

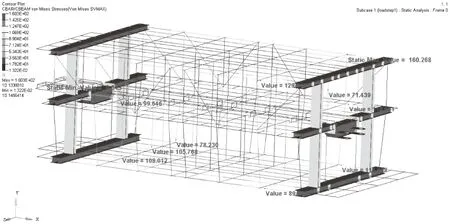
图3 拖车等效应力云图

对拖车模型开展模态分析，模态分析约束条件与静力分析一致，不添加载荷条件，分析拖车一阶模态应变能，一阶模态应变能较大的位置集中在壳单元和梁单元的连接位置，此处车体刚度梯度变化较大，最容易振动能量积累[8]，结合等效应力云图，这些部位最容易引起疲劳破坏，设计时可对这些部位局部加强。

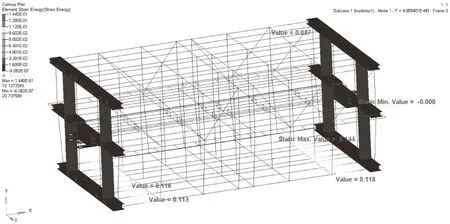
图4 拖车一阶模态应变能

2 拖车的尺寸优化分析

2.1 优化模型的建立

优化设计有三要素，即设计变量、目标函数和约束条件。设计变量是发生改变从而提高性能的一组参数；目标函数是要求最优的设计性能，是关于设计变量的函数；约束条件是对设计的限制，是对设计变量和其他性能的要求[8]。

运用最优化设计理论，以有限元软件Altair Optistruct为优化工具，在保证拖车强度和刚度的前提下，保持结构的形状和拓扑结构不变，寻求拖车的最佳截面尺寸，达到轻量化的目的[9]。拖车优化模型采用：

(1)

其中，Mass为模型总重量，X为设计变量，g(X)为设计空间内单元等效应力，Ωx为设计变量X的设计空间。

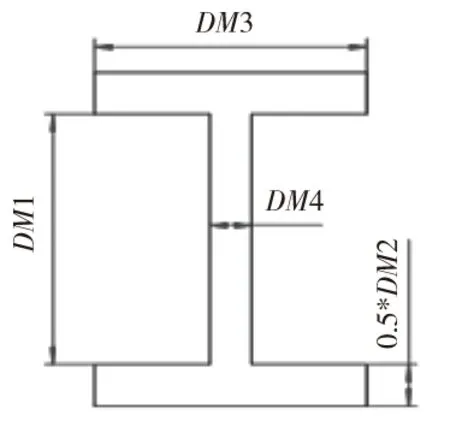
图5 H型梁截面优化变量

选取拖车主体梁的梁截面尺寸为优化对象，每个H型梁截面对应四个优化变量，如图5所示，其中DIM1∈[10，500]，DIM2∈[10，60]、DIM3∈[10，500]、DIM4∈[10，60]，本文将拖车主体梁型号分为5类，每种型号对应4个变量，此次优化分析变量数为20个。

2.2 优化结果分析与讨论

观察优化走势(重量变化)，重量先快速减小后缓慢减小。重量快速减少的部分叫做沿着算法方向(梯度方向，共轭方向)找边界；到达边界以后，开始沿着边界重新定义方向找最优解，这部分叫做约束优化下找最优解，如图7所示。所以重量快速减小是因为按照预定减小等效应力小于应力约束边界，缓慢减小是在满足应力约束边界的限制下去寻求重量最小的设计，这个时候重量减小率相比于沿算法方向明显降低。

优化后得到极限工况下每组H型钢的四个变量的最优取值，这四个最优数值离散分布而非国标H型钢，需将优化后的变量取值与国标H型钢表GBT11263—2017比对，找到最接近优化结果的国标H型钢。尺寸优化后静力分析结果如图8所示，优化前拖车重145 t，优化后重112 t，优化减重约22.76%。

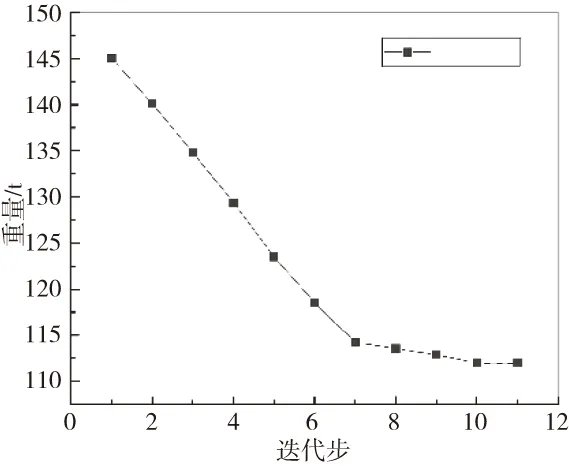
图6 优化迭代重量信息

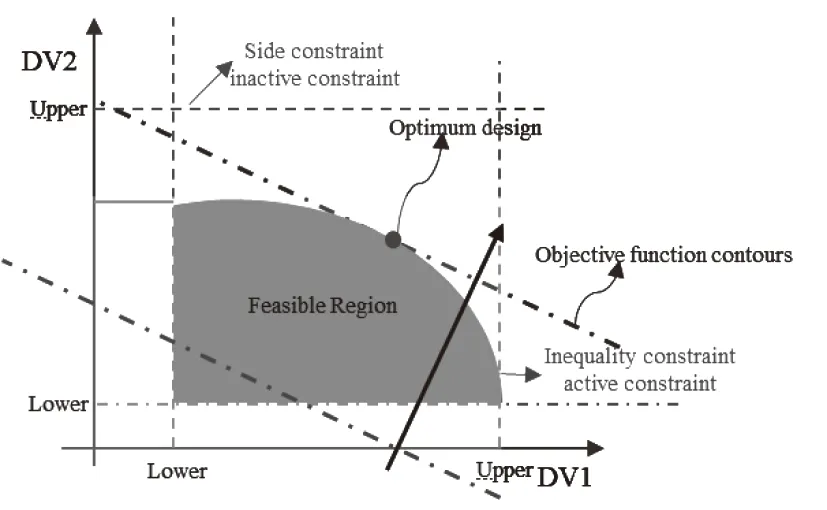
图7 可行性优化图示

拖车优化后的最大等效应力为179.97 MPa，小于Q355B钢的屈服极限355 MPa，拖车的安全系数为1.97，略小于推荐系数2，拖车的强度基本满足要求，最大变形小于30.48 mm，即拖车跨度的1/800，所以拖车的强度和刚度满足要求。但是需要进一步进行结构的局部调整，提高拖车的强度。尺寸优化后拖车整体应力分布更加均匀，应力较大区域增多，材料利用率明显提高。

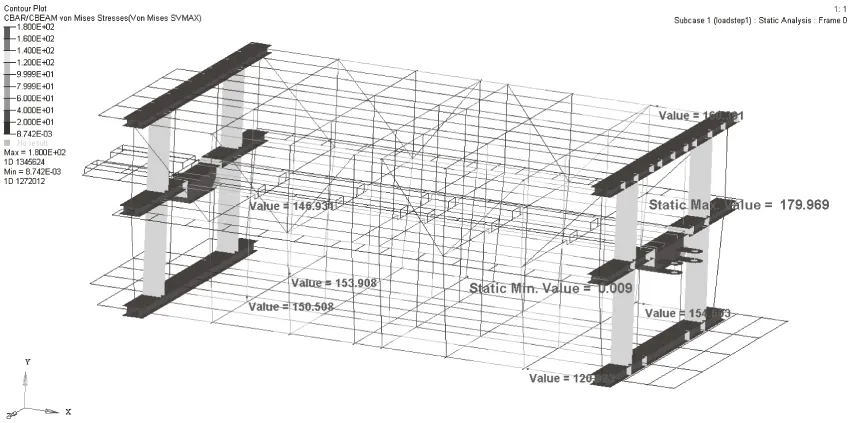
图8 拖车优化后等效应力云图

3 拖车局部优化分析

3.1 局部优化方案

对优化后的拖车模型开展模态分析，模态分析约束条件与静力分析一致，不添加载荷条件，分析优化后拖车模型的等效应力云图及一阶模态应变能云图，如图9所示，底层一阶模态应变能较大，在整体结构中刚度较薄弱或最容易产生应力集中，综合考虑等效应力云图及一阶模态应变能云图，依照等强度理论确定局部优化方案，如图10所示，依据尺寸优化结果将图10所示型钢选用更加安全的型号。

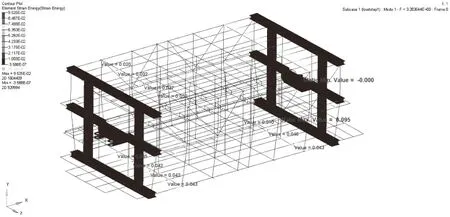
图9 拖车优化后一阶模态应变能云图

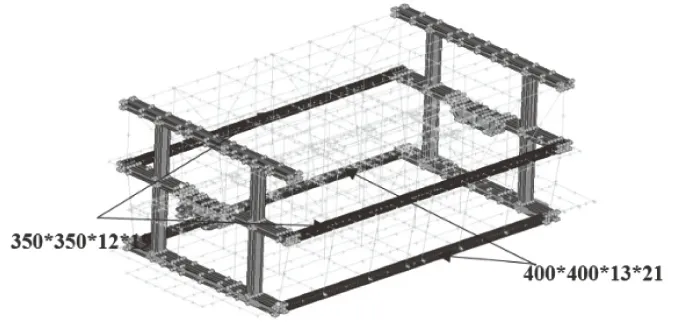
图10 拖车局部调整方案

3.2 局部调整结果分析

局部调整后拖车的最大等效应力为164.22 MPa，小于Q355B钢的屈服极限355 MPa，拖车的安全系数为2.16，大于推荐系数2，最大变形小于30.48 mm，即拖车跨度的1/800，所以拖车的强度和刚度满足要求。局部优化后拖车底层的一阶模态应变能明显降低，如图11所示，局部震荡得到明显改善，最大等效应力明显减低，应力分布更加均匀。如图12所示，局部优化后，拖车强度和刚度满足要求，减重约19.66%。

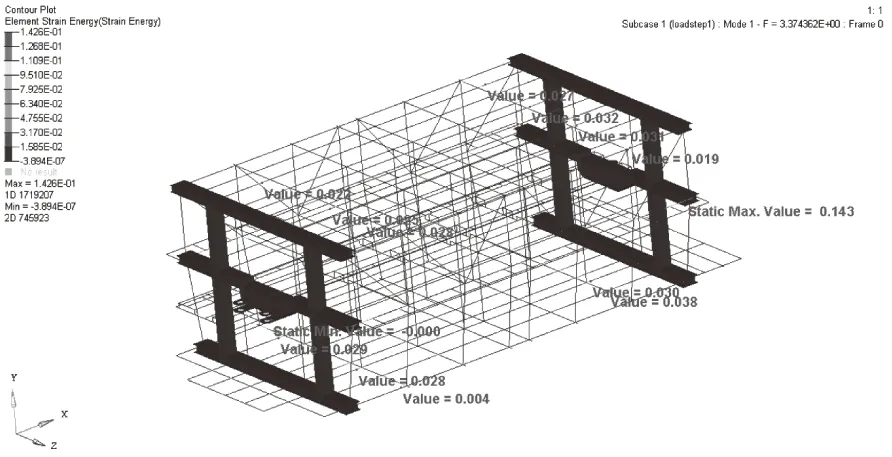
图11 局部调整后拖车一阶模态应变能云图

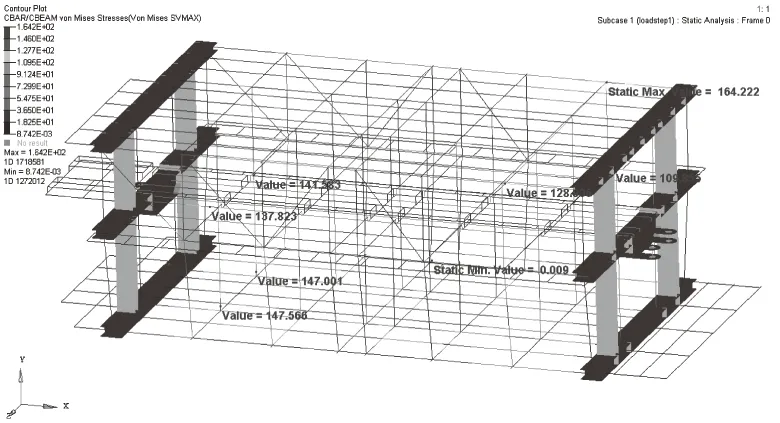
图12 局部调整后拖车等效应力云图

4 结论

本文运用Hyperwoks有限元分析软件，利用有限元理论方法，以某盾构拖车结构为对象，完整诠释了在现代设计方法中，将有限元理论运用于在盾构拖车开发和结构优化的整个过程。基于基础车的分析结果，对拖车结构进行优化改进，针对应力集中部位对结构进行了优化和调整，最终得到了优化的结构模型，并且通过强度对比分析，验证了方案的可行性。本文所采用的轻量化优化方案可在满足拖车结构安全的情况下，实现减重19.66%，优化效果显著。该分析与优化对拖车工程实际应用具有一定的指导意义。