极端温度作用下桥上CRTSⅡ型无砟轨道受力特性

闫斌，程瑞琦，谢浩然，曾志平

极端温度作用下桥上CRTSⅡ型无砟轨道受力特性

闫斌，程瑞琦，谢浩然，曾志平

(中南大学 土木工程学院，湖南 长沙 410075)

为研究极端温度作用下高速铁路简支梁桥与 CRTS Ⅱ型纵连板式无砟轨道相互作用，以5～32 m简支梁为例，建立考虑钢轨、扣件、轨道板、砂浆层、底座板、滑动层、摩擦板、端刺，以及梁体、墩台等构件的桥上 CRTS Ⅱ型无砟轨道系统精细化仿真模型，研究高温和严寒等极端温度条件下系统的受力与变形特征，探讨不同轨道伸缩刚度、滑动层摩擦因数和砂浆黏结力对系统受力与变形的影响。研究结果表明：在高温条件下，轨道板代替钢轨承受了更多伸缩力，轨道板轴向力最大值出现在主端刺处，易导致上拱破坏；正温度梯度作用下，轨道板上、下表面最大纵向应力差达10.1MPa，将引起翘曲变形导致端部砂浆层脱黏；在极寒条件下，轨道板最大纵向拉力出现在右端刺处，最大值达3.9 MPa，轨道板易发生断裂；底座板初始裂缝对轨道板及底座板的受力分布与变形产生不利影响；滑动层可有效减小梁轨之间的相互作用，适当增大砂浆黏结力有利于减小轨道板-底座板离缝和砂浆脱黏等病害的发生几率。

轨道工程；无缝线路；CRTS Ⅱ型；无砟轨道；极端温度；梁轨相互作用

桥上CRTS Ⅱ型无砟轨道是一种特殊的轨道结构形式，其采用纵向连续的轨道板和底座板作为承受纵向力的主要构件，在底座板和梁面之间铺设“两布一膜”滑动层减弱梁轨相互作用，实现了长大跨度桥上的连续铺设[1]。由于其轨道板和底座板纵向连续，当环境温度偏离锁定温度后，内部存在着极大的轴力。此外，由于混凝土导热性能较差，在太阳辐射的作用下，混凝土轨道结构中存在竖向温度梯度，引起轨道板翘曲变形。而轨道板一旦发生上拱破坏，修复难度极高，严重影响列车运行品质。因此，极端温度作用下桥上CRTS Ⅱ型板式无砟轨道无缝线路的受力与变形规律成为无砟轨道养护维修的关键课题之一。目前国内外学者对温度作用下桥上无砟轨道无缝线路受力与变形进行了广泛探讨，如YAN等[2-3]建立了适用于高速铁路中标准跨度简支梁、连续梁和斜拉桥的梁轨相互作用力学模型，分析了温度、活载和地震作用下梁轨系统的受力特性；陈嵘等[4]分析了温度荷载下桥上纵连板式无砟轨道的梁轨耦合规律；张鹏飞[5]研究了复杂温度荷载条件下多跨简支梁和大跨连续梁桥上无砟轨道的受力与变形特性。而极端温度条件下的桥上无砟轨道无缝线路受力与变形特性尚不明确。本文针对桥上CRTS Ⅱ型板式无砟轨道，以5～32 m简支梁为例，利用ANSYS软件建立了桥上CRTS Ⅱ型轨道系统精细化仿真模型，分析了极端温度条件下系统的受力变形特征，探讨了轨道伸缩刚度、滑动层摩擦因数和砂浆黏结力等关键设计参数对系统受力变形的影响。研究结果可为极端温度条件下桥上CRTS Ⅱ型板式无砟轨道结构的设计、养护和维修提供重要参考。

1 桥梁CRTSⅡ型板式无砟轨道计算模型

以5～32 m简支梁桥为研究对象，采用Beam4单元模拟钢轨，采用Beam188单元模拟轨道板、底座板和梁体，箱梁设置上、下翼缘刚臂，梁单元截面参数及材料特性按实际取值。采用非线性弹簧单元Combin39模拟线路纵向阻力、砂浆纵向阻力、滑动层纵向阻力、隔离层纵向阻力，采用线性弹簧单元Combin14模拟墩台、端刺、剪力齿槽及剪切钢筋的纵向阻力。桥跨两侧均设置100 m长的路基段以消除边界影响，本文假定路基上支承层与路基之间不产生相对位移。竖向考虑层间拉压刚度，横向考虑双线布置，所建立的桥上CRTS Ⅱ型轨道系统精细化仿真模型如图1所示。

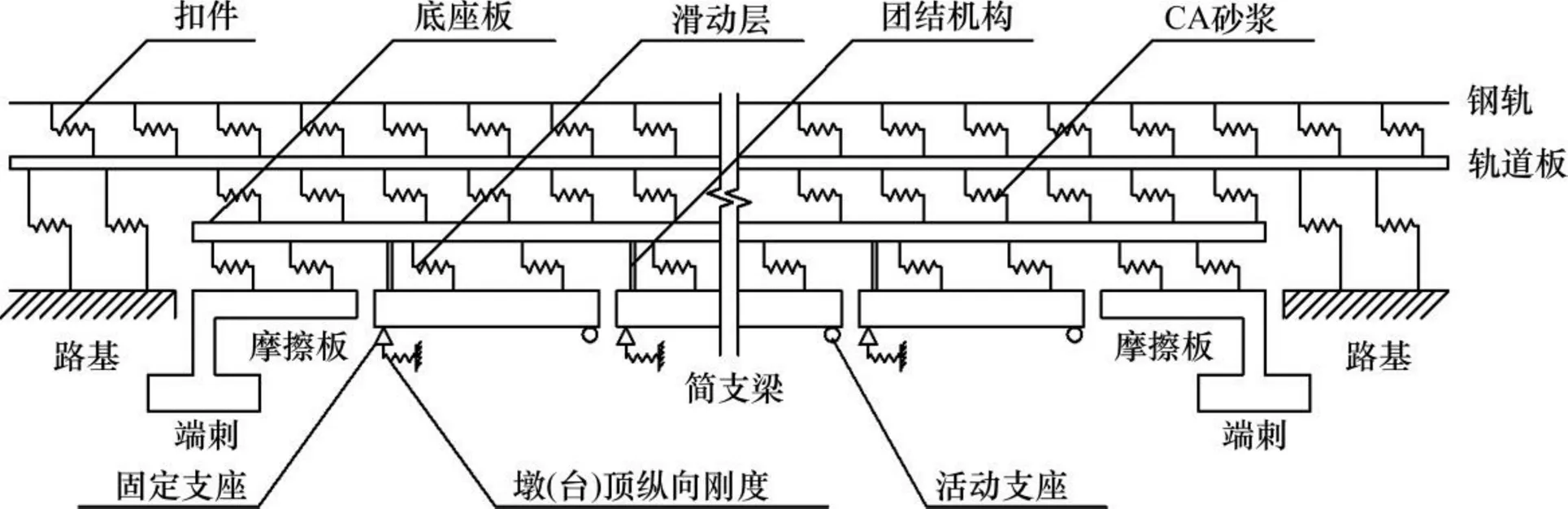
图1 桥上CRTS Ⅱ型板式无砟轨道力学模型

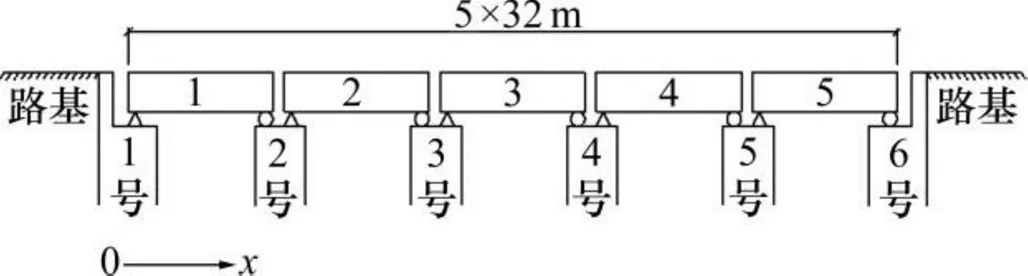
单位：m

钢轨采用CHN60轨，轨道板混凝土强度等级为C55，标准轨道板尺寸为6.45 m×2.55 m×0.2 m，通过张拉锁件使预制轨道板相互连接形成纵连轨道板。底座板为现场浇筑的纵连式结构物，其混凝土强度等级为C30，宽2.95 m，厚0.2 m。简支梁采用我国32 m高速铁路标准简支箱梁，梁体混凝土等级为C50。桥台处纵向刚度取3 000 kN/m，桥墩处纵向刚度取400 kN/m[6]，桥跨、支座布置及编号如图2所示。

扣件类型为WJ-8，扣件间距为0.65 m，每组扣件的纵向阻力在无载时取15 kN/组/轨，有载时取30 kN/组/轨，临界位移为2 mm。扣件垂向刚度取35 kN/mm[6]。砂浆层的纵向阻力根据博格公司的实验数据取值为63.88 kN/m，屈服位移为0.5 mm。滑动层纵向阻力用摩擦因数乘以单位长度的轨道结构自重来表示，滑动层的纵向摩擦因数取0.35，屈服位移为0.5 mm。

摩擦板的混凝土强度等级为C30，尺寸为50 m×9 m×0.4 m。摩擦板与上层底座板之间隔离层纵向摩擦因数取0.7，其屈服位移为5 mm。端刺纵向刚度取5×103kN/mm，剪力齿槽处的纵向连接视为刚性。

2 极端温度荷载模式的确定

我国《铁路无缝线路设计规范》(TB 10015—2012)[6]规定无砟轨道混凝土梁年温差取30 ℃；UIC规范[7]规定混凝土梁及结合梁桥年温差取±35 ℃。上述桥梁温度荷载按整体温升、温降考虑，这与桥梁的实际温度荷载存在一定差异。由于混凝土材料导热性较差，梁体中存在不均匀温度梯度。国内外规范对混凝土桥梁的温度梯度分布均有明确规定：我国《铁路桥涵混凝土结构设计规范》(TB 10092—2017)[8]规定混凝土箱梁的温度梯度可沿梁高和梁宽按指数函数取值；新西兰桥梁设计规范中桥梁温度荷载采用5次幂函数模式；美国桥梁设计规范中桥梁温度荷载采用双折线模式[9]。

由于混凝土材料热传导性能较差，无砟轨道内部也存在竖向温度梯度。相关研究表明[10-11]：无砟轨道结构的温度变化以日为周期，在无砟轨道厚度方向存在温度梯度，且离轨道板上表面距离越远，温度和温度梯度的变化幅度越小。我国《高速铁路设计规范》(TB 10621—2014)[12]中规定：无砟轨道正、负温度梯度宜取90 ℃/m和−45 ℃/m。德国博格板式无砟轨道最大正、负温度梯度分别取50 ℃/m，−25 ℃/m[5]。

本文在综合分析研究现状的基础上，确定了极端温度荷载模式的取值。在高温条件下，轨道板板面温度取60 ℃[10]，无砟轨道和桥梁的温度荷载均按《高速铁路设计规范》(TB 10621—2014)[12]取值：无砟轨道温度梯度取为90 ℃/m，桥梁的竖向温度梯度按《铁路桥涵混凝土结构设计规范》(TB 10092—2017)[8]规定的计算公式(1)取值。

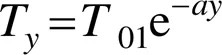
式中：T为计算点处的温差，℃；01为梁高方向温差，标准设计取值为20 ℃，铺设无砟轨道后，01可按标准设计的50%取值；为计算点至箱梁外表面的距离，m；为计算参数，规范中取值为5 m−1。

在极寒条件下，轨道板板面温度取−39 ℃[11]，无砟轨道和桥梁的温度荷载均按《高速铁路设计规范》(TB 10621—2014)[12]取值：无砟轨道温度梯度取为−45 ℃/m，桥梁的竖向温度梯度按《铁路桥涵混凝土结构设计规范》(TB 10092—2017)[8]规定的计算公式(2)取值。

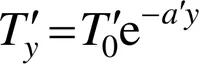
3 极端温度作用下桥上无砟轨道受力特征

3.1 高温条件下

采用第2节确定的高温条件下温度荷载，轨道结构纵向力计算结果见图3。

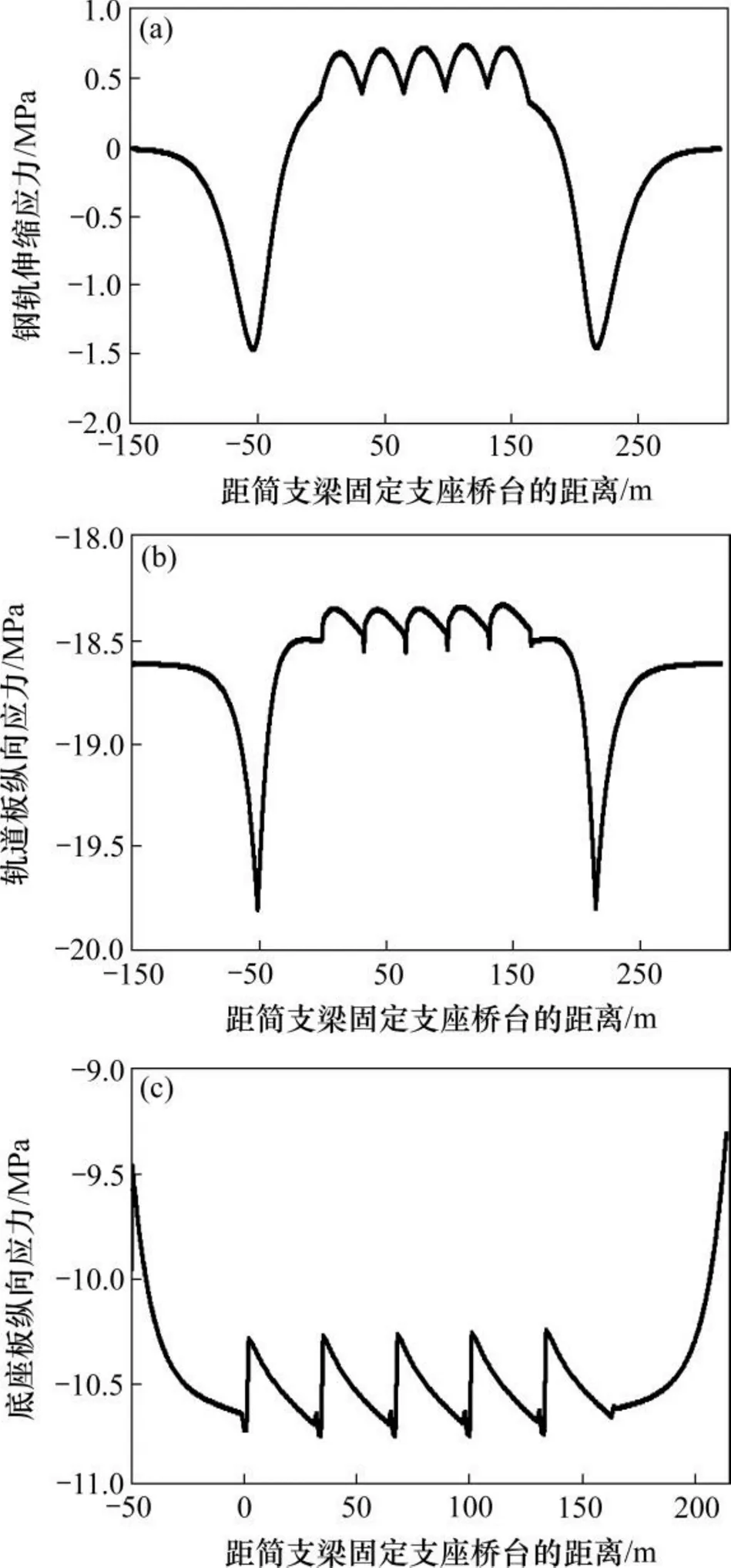
(a) 钢轨伸缩应力；(b) 轨道板纵向应力；(c) 底座板纵向应力

图3 高温条件下各轨道部件受力图

Fig. 3 Force diagram of track components under high temperature

由图3可知，最大钢轨伸缩压应力出现在端刺处，最大值为1.5 MPa。桥梁范围内钢轨伸缩拉力随桥跨布置有明显波动，最大伸缩拉应力为0.7 MPa，出现在桥梁中点处。轨道板最大纵向应力为−19.8 MPa，出现在端刺处，其上、下表面最大纵向应力差为−10.1 MPa。底座板最大纵向应力为−10.8 MPa，上、下表面最大纵向应力差为−9.0 MPa。底座板纵向力在剪力齿槽处发生突变，且变化值等于剪力齿槽纵向剪力，剪力齿槽最大纵向剪力为302.2 kN。桥梁纵向力从活动端至固定端呈增加趋势，桥梁最大纵向力为−602.9 kN。

可见，高温条件下轨道板和底座板内部纵向压力较大，极有可能发生上拱破坏，且由于正温度梯度的存在，无砟轨道上、下表面纵向应力差较大，会引起翘曲变形，应该对极端高温地区的轨道板及底座板做特殊配筋设计，防止其出现较大的变形。

高温条件下轨道结构的位移计算结果见图4。

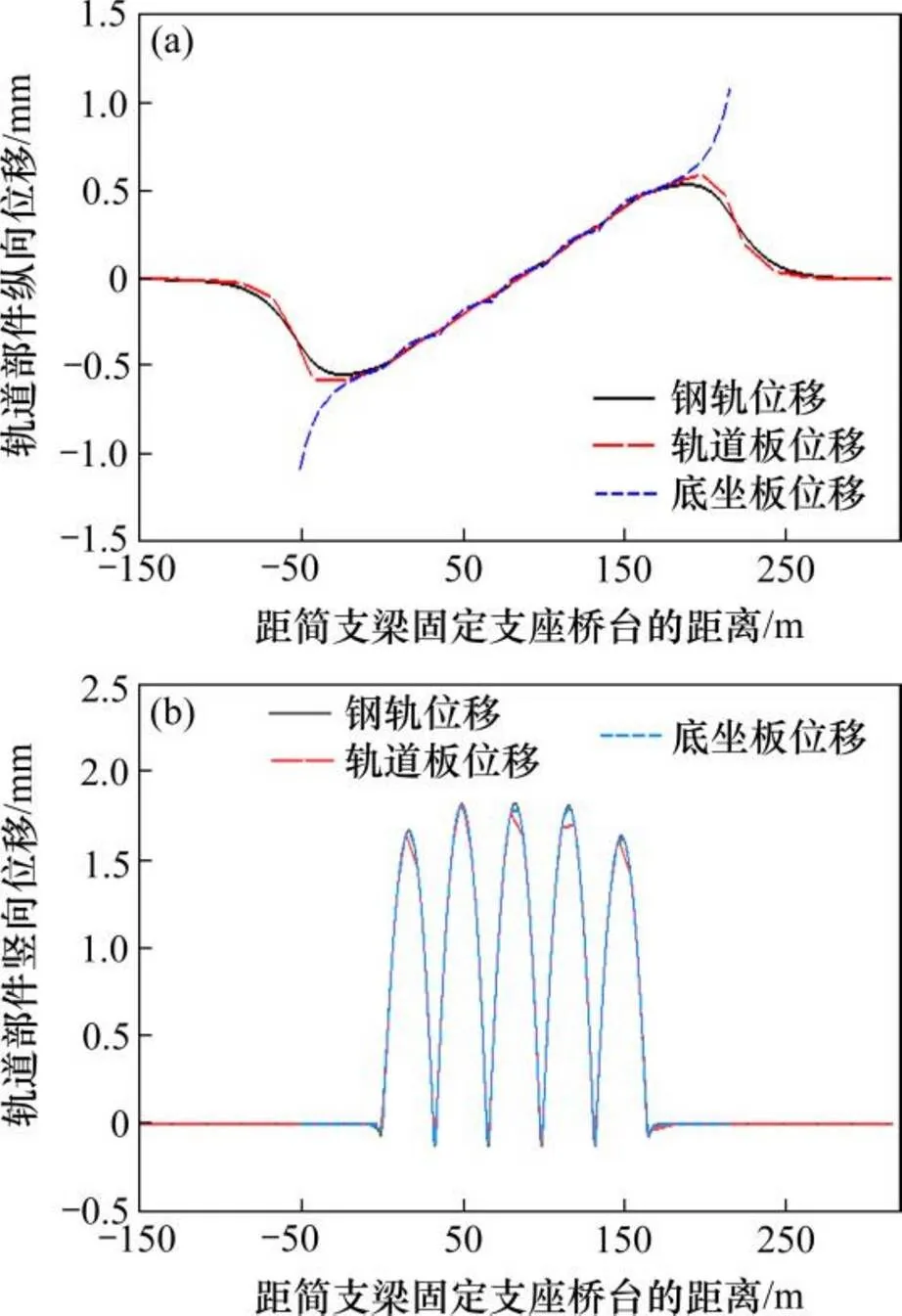
(a) 各轨道部件纵向位移；(b) 各轨道部件竖向位移

由图4可知，钢轨、轨道板及底座板均在每跨桥梁范围内发生上拱变形，钢轨最大竖向位移在跨中处达到1.8 mm。钢轨、轨道板及底座板的纵向位移分布规律相似，最大位移量和位移变化幅度从下至上逐层减小，其最大位移量均在主端刺附近出现，最大值分别为0.5，0.6和1.1 mm。底座板两端纵向位移与两侧端刺纵向位移相等，可见端刺决定了底座板纵向位移，进而影响其他轨道部件的变形。钢轨−轨道板及轨道板−底座板纵向相对位移最大值出现在端刺处，分别为0.1 mm和0.7 mm，桥梁范围内的纵向相对位移极小。

每跨桥梁纵向位移分布相似，从固定端至活动端线性增加，最大位移量为5.3 mm。由于滑动层削弱了底座板与梁体间的相互作用，底座板没有随桥梁发生较大变形，底座板和桥梁的最大相对位移为4.9 mm。

3.2 极寒条件下

采用第2节确定的极寒条件下温度荷载，考虑轨道板和底座板伸缩刚度的折减，折减系数为0.3，轨道结构纵向力计算结果见图5。

由图5可知，钢轨附加伸缩力较小，两侧摩擦板范围内出现伸缩拉应力，钢轨最大伸缩拉应力为0.7 MPa。桥梁范围内出现伸缩压应力，在第一跨桥梁中点处出现最大伸缩压应力，最大值为0.5 MPa。

轨道板最大纵向拉应力为3.9 MPa，出现在右侧端刺处，轨道板易发生断裂，底座板最大纵向拉应力为2.7 MPa。剪力齿槽最大纵向剪力为−286.4 kN。桥梁纵向力从活动端至固定端呈增加趋势，桥梁纵向力最大值为597.4 kN。

极寒条件下轨道结构的位移计算结果见图6。

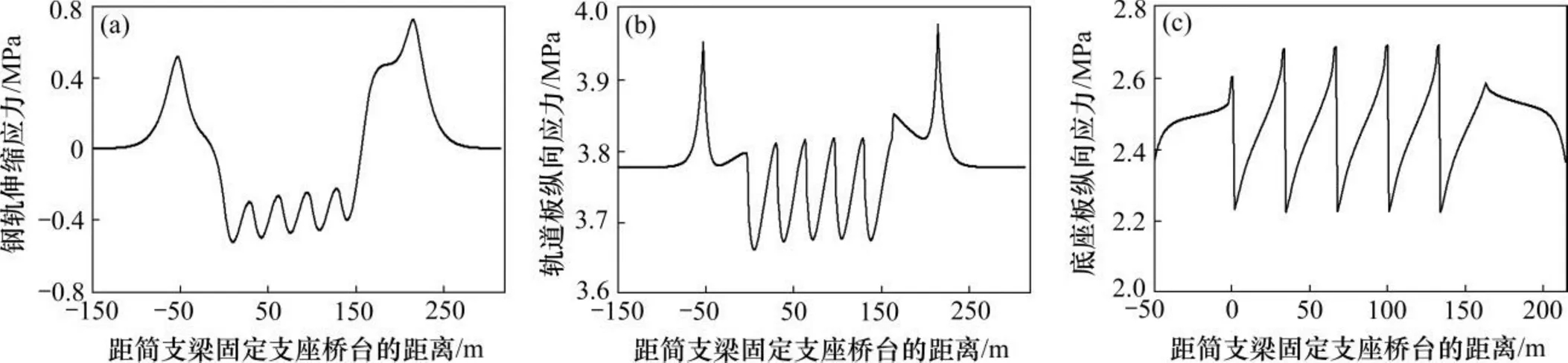
(a) 钢轨伸缩应力；(b) 轨道板纵向应力；(c) 底座板纵向应力

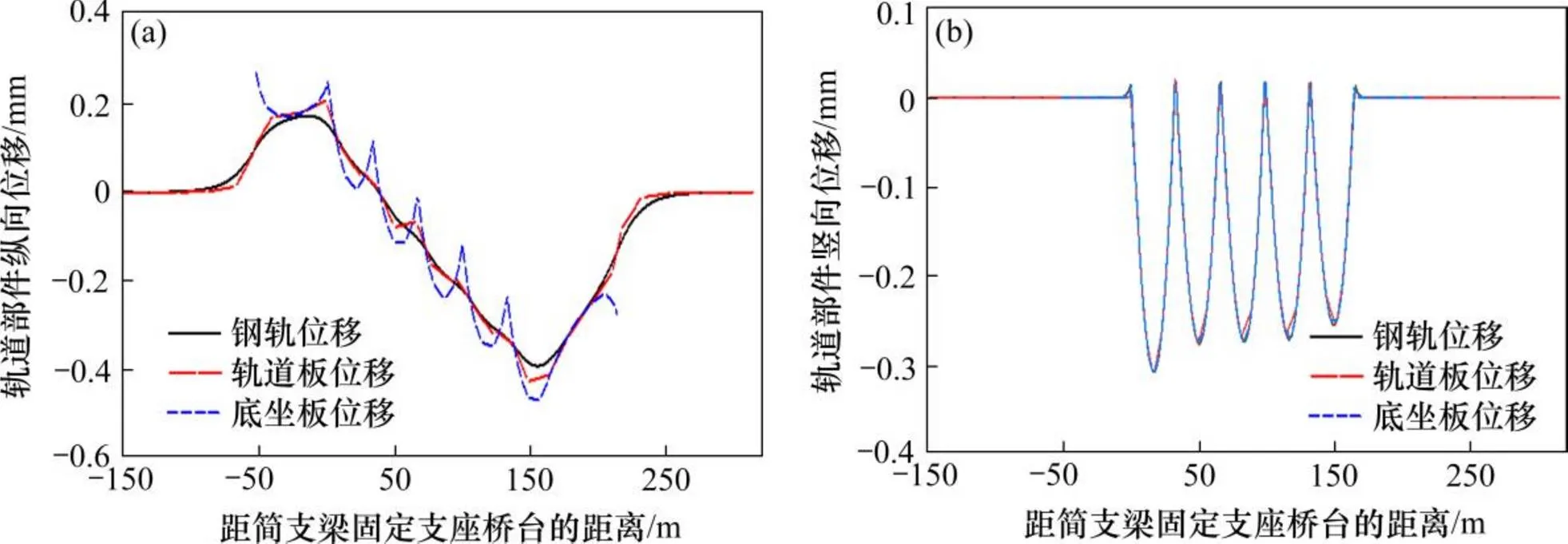
(a) 各轨道部件纵向位移；(b)各轨道部件竖向位移

由图6可知，钢轨、轨道板及底座板均在每跨桥梁范围内发生下凹变形，钢轨最大竖向位移为0.3 mm，出现在第一跨简支梁跨中处。钢轨、轨道板及底座板的纵向位移量和桥跨内位移变化幅度从下至上逐层减小，在剪力齿槽处有较大波动。钢轨、轨道板、底座板最大纵向位移出现在右侧桥台，最大值分别为0.4，0.4和0.5 mm。钢轨−轨道板及轨道板−底座板纵向相对位移最大值分别为0.1 mm和0.2 mm，左右两边跨的层间相对位移大于中间各跨。每跨桥梁位移分布几乎相同，从固定端至活动端线性增加，最大位移为5.1 mm，底座板−桥梁最大纵向相对位移为4.7 mm。

4 极端温度作用下桥上无砟轨道受力与变形影响因素分析

4.1. 轨道板/底座板伸缩刚度

以高温条件为例，不同伸缩刚度条件下轨道及桥梁结构受力及位移最大值见表1。

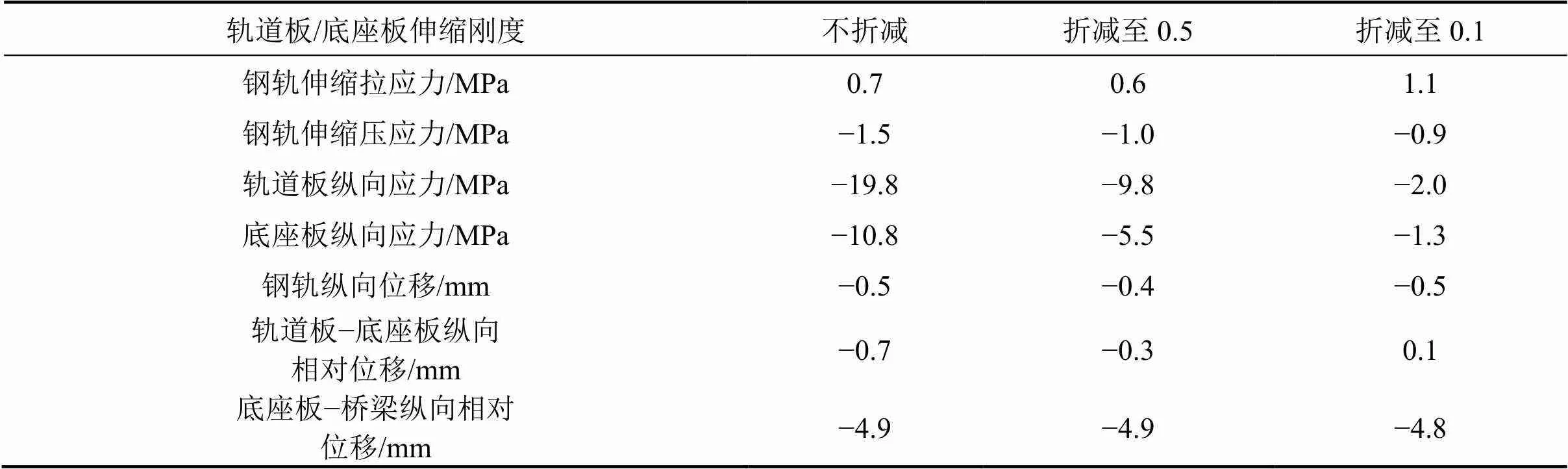
表1 不同伸缩刚度条件下计算结果最大值

由表1可知，随着伸缩刚度的折减，路基段和主端刺附近的钢轨伸缩压应力减小，桥梁范围内的钢轨伸缩拉应力增加，轨道板和底座板纵向力明显减小。桥梁范围内的钢轨、轨道板、底座板纵向位移及层间相对位移均明显增大。

4.2 桥上滑动层摩擦因数

以高温条件为例，不同滑动层摩擦因数条件下轨道及桥梁结构受力及位移最大值见表2。

由表2可知，随着滑动层摩擦因数增大，钢轨、轨道板、底座板及桥梁、墩台、剪力齿槽的纵向力随之增大，各轨道部件的纵向位移及层间相对位移均增大。可见，滑动层可有效减小梁轨间的相互作用，桥梁和轨道结构的受力与位移随摩擦因数增大而增大。

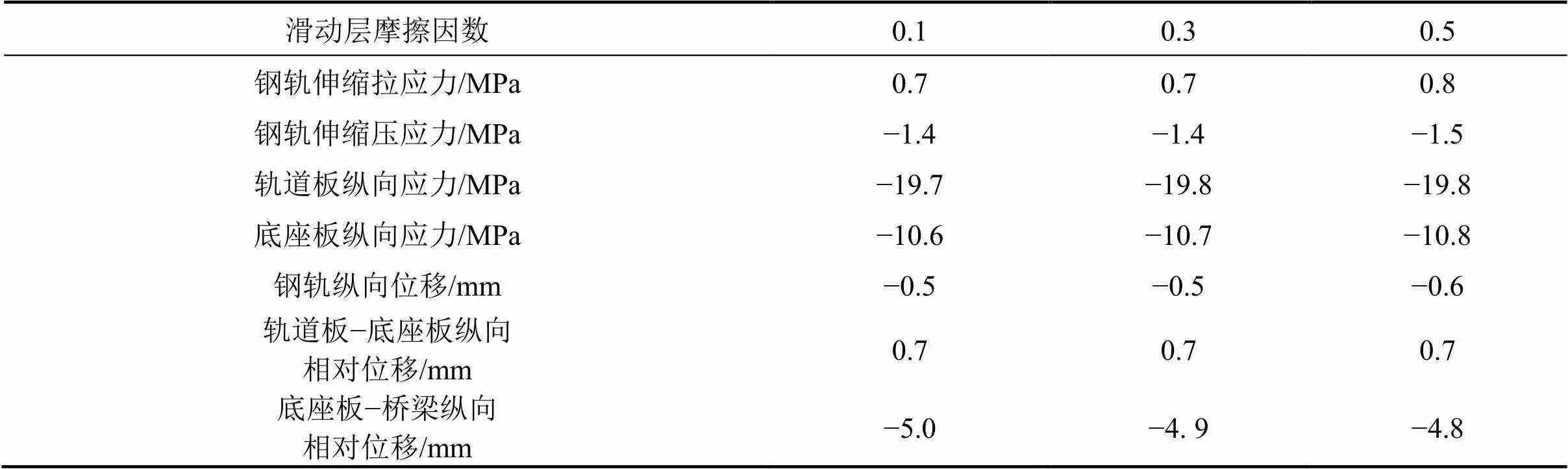
表2 不同滑动层摩擦因数条件下计算结果最大值

4.3 砂浆黏结力

以高温条件为例，不同砂浆黏结力条件下轨道及桥梁结构受力及位移最大值见表3。

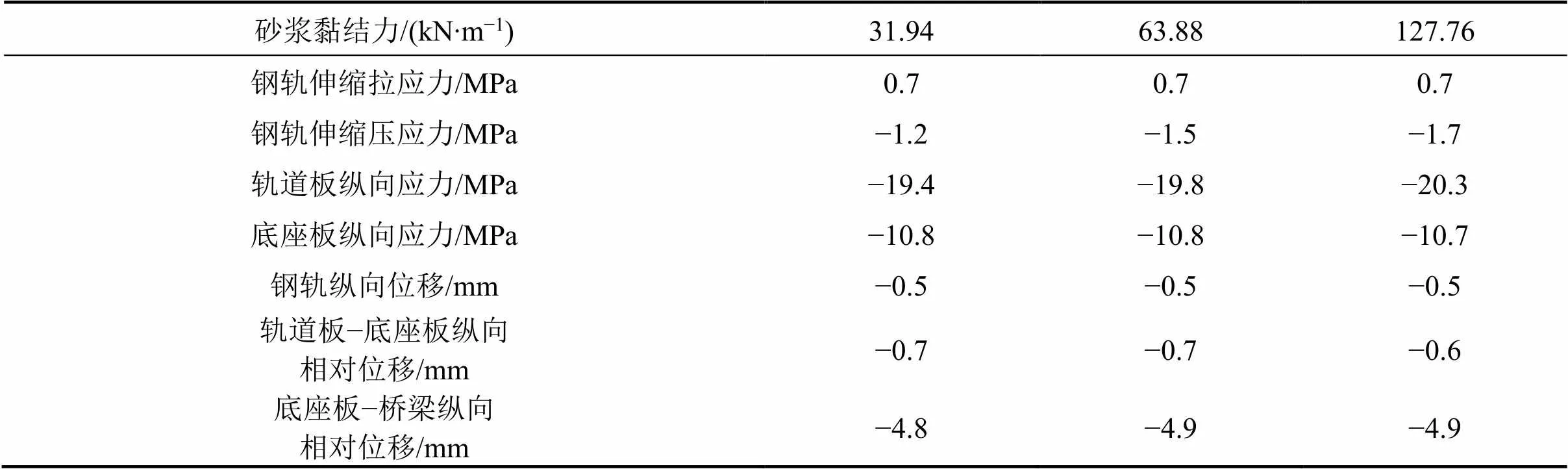
表3 不同砂浆黏结力条件下计算结果最大值

由表3可知，随着砂浆黏结力增大，主端刺附近的钢轨伸缩力和轨道板纵向力明显增大，底座板纵向力也随着增大。轨道板与底座板间的纵向相对位移明显减小，出现轨道板−底座板离缝和砂浆脱黏的概率会降低。增大砂浆黏结力对系统的受力变形是有利的。

5 结论

1) 桥上纵连板式无砟轨道的钢轨伸缩力较小，其伸缩力分布随梁跨布置波动，在端刺处出现最大伸缩力。纵向连续的轨道板和底座板承受了较大的温度力，温度力最大值出现在端刺位置，底座板纵向力在剪力齿槽处突变，且变化值等于剪力齿槽的纵向剪力。

2) 在高温条件下，轨道板内部最大纵向压应力达19.8 MPa，出现在端刺处，易发生上拱破坏。正温度梯度导致轨道板上、下表面最大纵向应力差达10.1 MPa，会引起翘曲变形导致端部砂浆层脱黏。钢轨、轨道板及底座板均在每跨桥梁内发生上拱变形，钢轨最大竖向位移在跨中处达到1.8 mm。由于滑动层的存在，底座板和桥梁的最大纵向相对位移为4.9 mm。

3) 在极寒条件下，轨道板最大纵向拉应力在右端刺处达3.9 MPa，轨道板易发生断裂。底座板最大纵向拉应力为2.7 MPa。各轨道部件最大纵向位移和位移变化幅度从下至上逐层减小，在剪力齿槽处有较大波动。底座板和桥梁最大纵向相对位移为4.7 mm。

4)底座板存在初始裂缝时，传递纵向力和抵抗纵向变形的能力减弱，对轨道板及底座板的受力与变形产生不利影响。滑动层可有效减小梁轨之间的相互作用，应严格控制滑动层施工质量，确保桥上滑动层的摩擦因数在合理范围内。增大砂浆黏结力有利于桥上CRTS Ⅱ板式无砟轨道的受力与变形，减小轨道板−底座板离缝和砂浆脱黏等病害的发生几率。

[1] Bögl Company of German. Number 1-8 technical report of Bogl longitudinal connected ballastless track on Jing-Jin intercity high-speed railway bridges[R]. Jing-Jin Intercity High-speed Railway Design Department of Bögl Company of German, 2006.

[2] YAN Bin, ZHANG Gaoxiang, HAN Zhongshu, et al. Longitudinal force of continuously welded rail on suspension bridge with length exceeding 1 000 m[J]. Structural Engineering International, 2019, 29(3): 390− 395.

[3] DAI Gonglian, YAN Bin. Longitudinal forces of continuously welded track on high-speed railway cable-stayed bridge considering impact of adjacent bridges[J]. Journal of Central South University, 2012, 19(8): 2348−2353.

[4] 陈嵘, 邢俊, 谢铠泽, 等. 温度荷载下纵连式无砟轨道梁轨耦合作用规律[J]. 铁道工程学报, 2017, 34(3): 15− 21. CHEN Rong, XING Jun, XIE Kaize, et al. The continuous-slab-track coupling laws between the bridge and track under temperature loads[J]. Journal of Railway Engineering Society, 2017, 34(3): 15−21.

[5] 张鹏飞. 复杂荷载条件下桥上CRTS Ⅱ型板式无砟轨道无缝线路纵向力研究[D]. 北京: 北京交通大学, 2018. ZHANG Pengfei. Researches on longitudinal force of the CWR with CRTS Ⅱ slab ballastless track on bridge under complex load conditions[D]. Beijing: Beijing Jiaotong University, 2018.

[6] TB 10015—2012, 铁路无缝线路设计规范[S]. TB 10015—2012, Code for design of railway continuous welded rail[S].

[7] UIC. UIC 774-3 Track/bridge interaction. Recommendations for calculations[S]. Paris: International Union of Railways, 2001.

[8] TB 10092—2017, 铁路桥涵混凝土结构设计规范[S]. TB 10092—2017, Code for design of concrete structures of railway bridge and culvert[S].

[9] 朱禹,李成辉.梁体温差对桥上无砟轨道横向稳定性影响研究[J]. 铁道标准设计, 2017, 61(12): 46−50. ZHU Yu, LI Chenghui. Study on the influence of beam temperature difference on the lateral stability of ballastless track on bridge[J]. Railway Standard Design, 2017, 61(12): 46−50.

[10] 孙泽江, 王泽萍, 汪杰, 等. 极端高温天气下CRTSⅡ型板式无砟轨道温度分析[J].铁道标准设计, 2018, 62(11): 64−68. SUN Zejiang, WANG Zeping, WANG Jie, et al. Temperature analysis of CRTS Ⅱ slab ballastless track in extremely hot weather[J]. Railway Standard Design, 2018, 62(11): 64−68.

[11] 郭超, 陆征然, 吕菲, 等. 严寒地区CRTSⅡ型无砟轨道板温度特性研究[J]. 铁道工程学报, 2016, 33(9): 29−34. GUO Chao, LU Zhengran, LÜ Fei, et al. Research on the temperature features of CRTS Ⅱ ballastless track slab in severe cold region[J]. Journal of Railway Engineering Society, 2016, 33(9): 29−34.

[12] TB 10621—2014, 高速铁路设计规范[S]. TB 10621—2014, Code for design of high-speed railway [S].

Mechanical characteristics of CRTSⅡ ballastless track on bridge due to extreme temperature load

YAN Bin, CHENG Ruiqi, XIE Haoran, ZENG Zhiping

(School of Civil Engineering, Central South University, Changsha 410075, China)

Taking 5～32 m simply supported beam bridge as an example, a refined simulation model of CRTS Ⅱ track system on bridge was established to study the interaction between simply supported beam bridge of high- speed railway and CRTS Ⅱ ballastless track under extreme temperature. The rail, fastener, track plate, mortar layer, base plate, sliding layer, friction plate, end thorn, beam body, pier, abutment and other components were considered. The stress and deformation characteristics of the integrated system under extreme high and low temperature levels were studied. The influences of different expansion rigidity of track, friction coefficient of sliding layer and adhesion of mortar on stress and deformation were discussed. As revealed, the track plate bears more expansion force instead of rail, and the maximum axial force of track plate appears at terminal spine, which is easy to cause the upper arch failure. Under the positive temperature gradient, the maximum longitudinal stress difference between the upper and lower surfaces of track plate is up to 10.1 MPa, which will cause warping deformation and lead to the debonding of mortar layer. Under the severe cold condition, the maximum longitudinal tensile force of track plate appears at the right terminal spine, and the maximum value reaches 3.9 MPa, which is easy to cause track plate breakage. The initial crack in base plate will have an adverse effect on the stress and deformation of track plate. The sliding layer effectively weakens the beam-rail interaction, and the increase of mortar adhesion is beneficial to reduce the probability of the disease such as track plate gap and mortar debonding.

track engineering; continuously welded rail; CRTSⅡ; ballastless track; extreme temperature; beam-rail interaction

10.19713/j.cnki.43−1423/u.T20200473

U213.912

A

1672 − 7029(2021)04 − 0830 − 07

2020−05−29

国家重点研发计划项目(2017YFB1201204)；中央高校基本科研业务费专项资金资助项目(2020zzts643)

曾志平(1975−)，男，湖南宁乡人，教授，博士，从事铁路轨道结构研究；E−mail：hzzp7475@126.com

(编辑 阳丽霞)