时段偏好的高铁开行方案的双层规划方法

黄志鹏，田志强，司晓鑫

时段偏好的高铁开行方案的双层规划方法

黄志鹏1，田志强1，司晓鑫2

(1. 兰州交通大学 交通运输学院，甘肃 兰州 730070；2. 中国铁路兰州局集团有限公司 兰州车务段，甘肃 兰州 730050)

在一条拥挤的高速铁路客运走廊上，通常有多列平行车次的列车在不同的时段运行，旅客在出行时具有较大的选择空间。旅客对出行时段的偏好是影响旅客需求分布的最重要因素，最大限度地满足旅客对出行时间的偏好需求，并合理制定列车开行方案引导旅客合理出行以避免出行拥挤是本文的研究目的。首先分析影响旅客出行时段偏好的2个重要因素，吸引度与拥挤度。据此构建旅客出行阻抗函数，并建立一个双层规划模型，上层规划是以运营成本最小为目标的整数规划模型，用于确定列车停站方案和开行频率；下层规划是一个用户平衡模型，用于计算客流在优化的停站方案上基于用户均衡的分配结果。最后，根据模型特点设计了嵌套Frank-Wolfe算法的启发式算法，并通过仿真计算对模型和算法的可行性进行了验证和分析。

高速铁路；列车开行方案；双层规划；用户平衡；启发式算法

旅客选择高铁出行不仅仅是对传统铁路客运核心产品——“位移”的需求，同时对旅客出行品质提出了更高的要求，而出行时段的选择则是旅客最关心的需求之一。旅客会根据自身的出行习惯、出行目的和出行经验来选择最理想的出行时段。在高铁全天运营的各个时段上，旅客出行需求具有不均衡特征，表现出明显的时段偏好性。另一方面，铁路部门在不同时段组织的各种停站方案的列车也是影响旅客出行选择的关键因素。因此，基于旅客对出行时段的偏好，优化各个出行时段列车的停站方案，使旅客出行需求与列车停站方案具有良好的耦合关系是本研究的主要目的。国外学者一般是将旅客列车停站方案作为列车时刻表(Train Timetable Problem, TTP)优化问题的一个重要部分进行研究。其中大部分是站在运输效益最大化角度进行的研究。YUE等[1−2]用0-1决策变量表示列车在中间站是否停站，构建了一个以运输收益最大为目标的TTP模型求解了大规模网络条件下高速铁路列车停站优化问题。QI 等[3]以列车空座位运行距离和所有列车总停站数最小为目标建立了一个多目标线性规划模型优化列车停站方案。近十年来，综合考虑旅客的出行质量，将旅客出行时间或出行费用优化纳入TTP优化模型的研究较多。Jens等[4]建立了一个双层规划模型优化旅客列车停站问题。SHANG等[5]通过构造多商品流模型，优化客流的分配和列车的停站方案。考虑到列车停站次数对运输效益的影响，部分学者将列车停站次数作为优化目标或者约束条件。NIU等[6]以旅客总等待时间最小为目标研究了时变条件下一条高铁走廊的列车时刻表优化问题。李得伟等[7]以总停站次数最少为目标，将节点服务频率、站间服务可达性、单个列车停站次数等作为主要约束条件，构建列车停站方案的非线性规划模型。张小炳等[8−10]从列车停站数量的均衡性和区间的可达性出发，建立高速铁路列车停站方案的非线性多目标优化模型。赵杰群等[11]以列车停站费用最小化为优化目标，建立了机会约束模型优化了列车停站方案问题。刘璐等[12]基于旅客需求的时变特征，建立了时空状态三维出行网络，协同优化了列车运行图和列车停站方案问题。考虑到旅客出行需求与运输企业效益的博弈关系，一些学者试图建立双层规划模型对该问题进行数学描述，并取得了一定的成果。邓连波等[13−15]通过建立双层规划模型优化列车停站方案。模型的上层为旅客广义出行费用最小和列车停靠站数量限制，下层为多类用户均衡客流分配模型。本文拟分析影响旅客出行时段偏好性的主要因素，建立一个双层规划模型来优化一条高铁线路上不同时段各种停站方案列车的开行数量，并依据用户平衡规则将客流分配在各个出行时段上。论文的主要创新点：首先，将旅客的出行时段偏好与列车停站方案结合起来协同优化，并将多OD客流需求分配在各个出行时段上。其次，不同于以往周期化的停站方案优 化[16]，本文制定的停站方案按照出行时段分别优化停站方案。

1 问题分析

1.1 列车类型和时段划分

1.2 旅客出发时段偏好

1.2.1 出发时段的吸引度

旅客对各个出发时段的偏好性，表现为不同时段对旅客的吸引度有很大差异。这种差异是客观存在的，并受到多种客观因素的影响。如通勤客流占全部客流比重较大的车站，对旅客吸引度最高的时段为早晚高峰时段；又如旅客总是期望在城市公交方便的白天时段出行等等，均为影响旅客选择出行时段的客观因素。

图1 出发时段吸引度的三角模糊数分布

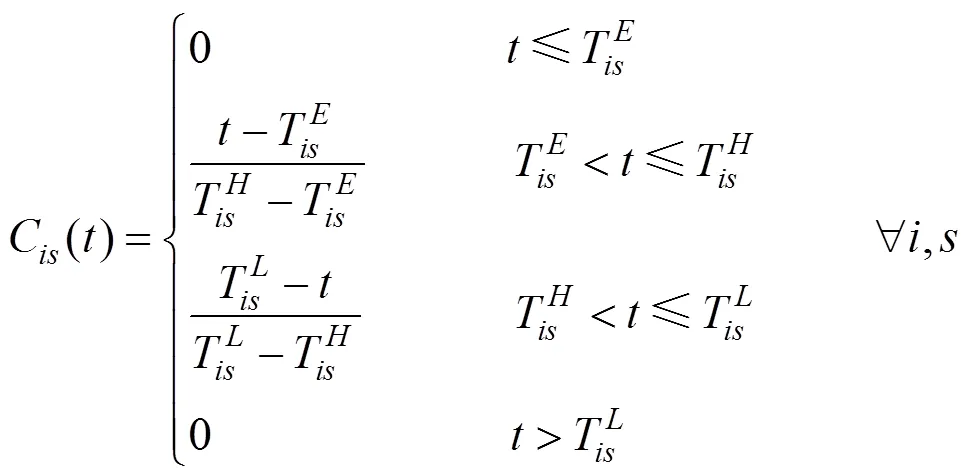
1.2.2 出发时段的拥挤度

旅客对各个出行时段的偏好性，还表现为旅客对不同时段拥挤度的选择。当某个出行时段的吸引度较大时，大量的旅客均期望在这个时段出行。这时，这个时段的拥挤度也会大大提高。如旅客选择在吸引度较大的时段出行时，有可能因时段需求旺盛而未能购得车票；或者旅客为了确保能够在这个时段出行，必须提前很久购票，使得旅客的出行灵活性降低，带来很大的不便。

1.2.3 出发时段偏好的量化

2 模型和算法

2.1 数学模型

2.1.1 符号定义

2.1.2 上层规划

上层规划的目标是铁路运输企业的运营成本最小。不同停站方案的列车由于能耗和占用沿途车站设备的因素，其运营成本是不相同的。

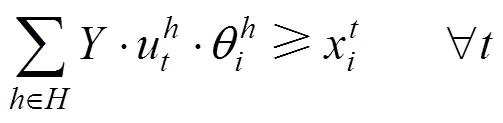
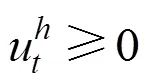
2.1.3 下层规划

下层规划是一个符合Wardrop第一原理的用户平衡配流模型。

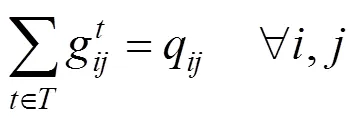
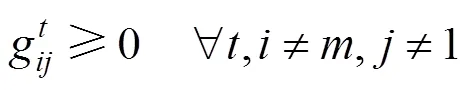
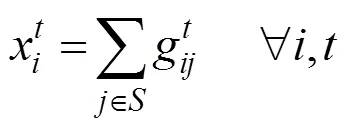
2.1.4 上、下层的联系

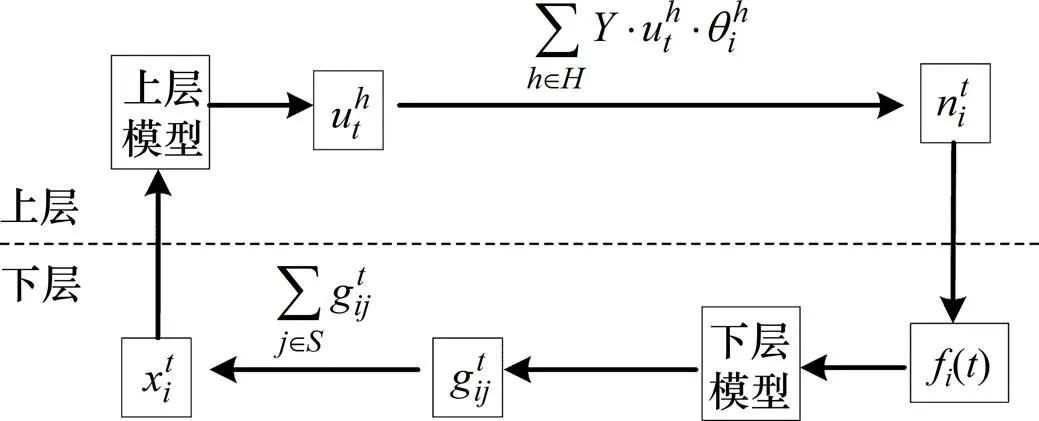
图2 上下层规划的数据交换

这样，上层规划的列车开行方案和下层规划的客流分配结果之间，会循环反复的调整，直至达到满意解为止。

2.2 算法设计

论文所建模型是一个双层规划问题，它被公认为是求解极其困难的NP完全问题。本文设计了嵌套Frank-Wolfe方法的启发式算法进行求解。算法流程如下。

Step 4整数编码：对Step 1产生的0～1编码染色体中“1”的基因位置随机赋一个整数值，并满足式(6)和式(7)的约束。

3 算例

3.1 参数设置

本文以兰州西—西安北高铁为例。为了方便表示，将兰州西站编号为1，按照列车上行方向依次编号，其中兰州西、西安北为始发、终到车站，必停车；另外在4个区域中心所在的定西北站、天水南站、宝鸡南站、咸阳秦都站必停车；铁路运输部门将列车在其他车站的停车次数设置为0～2次，则全部备选停站方案共11种，如图3所示。

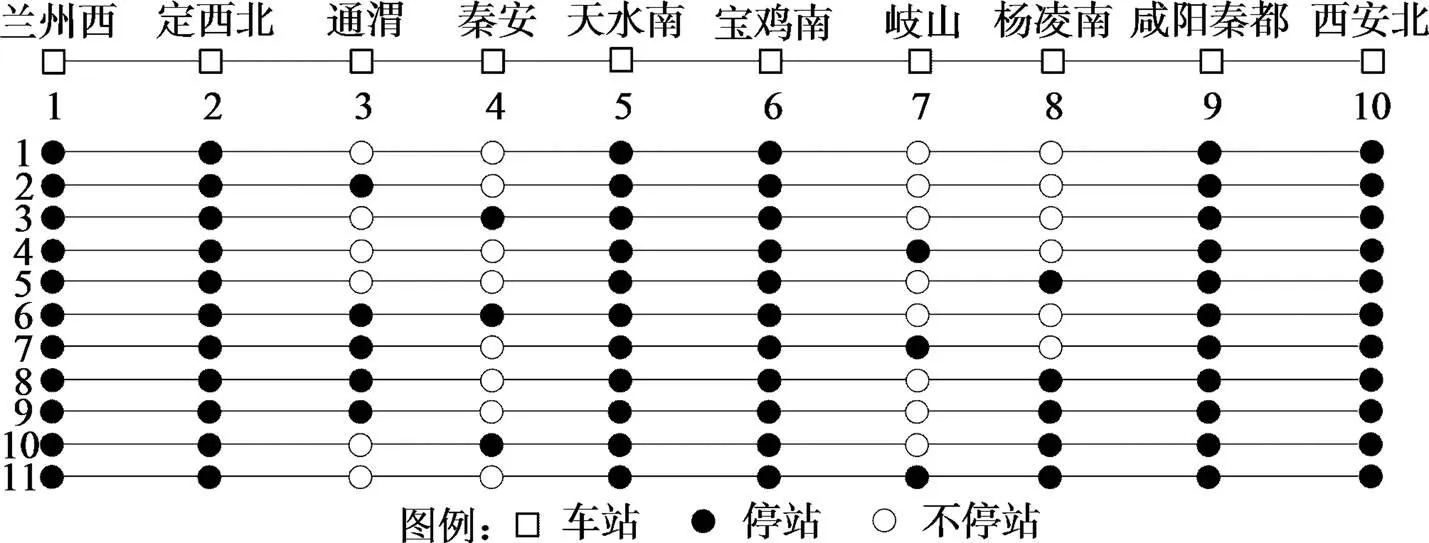
图3 列车停站备选方案

该高铁上所有起讫点(OD)间的客流需求如表1所示。本文以1 h为一个时段，将高铁全天的发车时间(6:00～22:00)划分为16个时段，并将6:00～7:00标记为时段1，按照时间顺序依次编号2,3,…,16。各出发时段的吸引度，如表2所示。其中，距离始发站较远的车站，每日首列车到达该站时的时段会相应延迟，如车站3到9，将其吸引度设置为0。

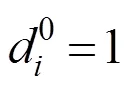
表1 OD客流需求

3.2 计算结果

通过matlab2014a软件编程，对该算例进行求解，下层规划计算结果如表5所示。各上车站的OD客流被分配在各个时段上出行，各时段客流具有明显的波动性。同一车站旅客出行的阻抗值旅客出行阻抗满足UE平衡法则，在误差范围内均相等，符合Wardrop第一原理[17]。

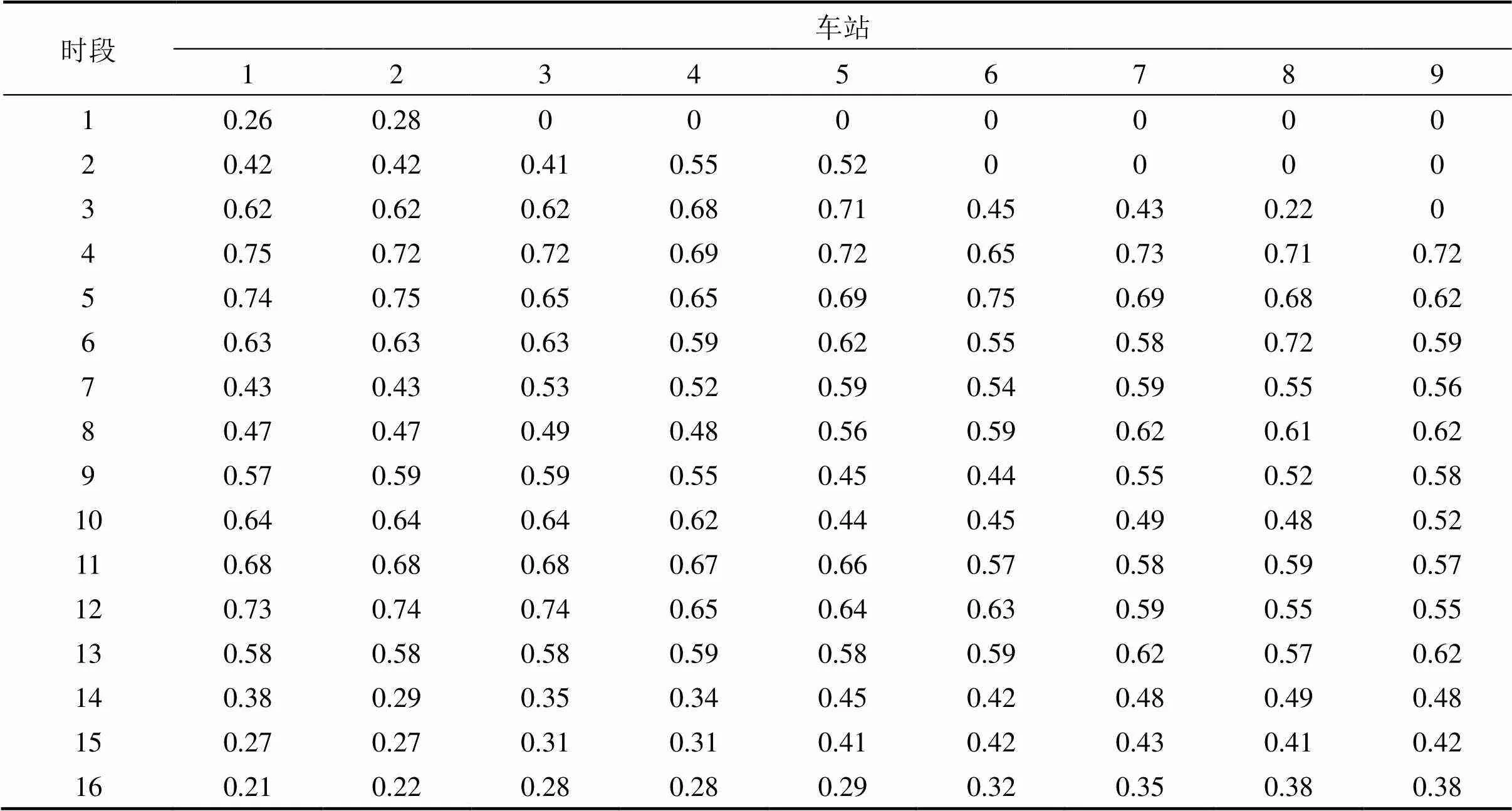
表2 各个车站在各出发时段的吸引度参数

表3 不同停站方案列车的开行成本

表4 各出发站的服务能力

通过下层规划的配流结果和上层规划开行方案的迭代，最终经过100代的进化筛选，得到满意解。共开行95列车，其中，第12时段开行列车数量最多，为9列，第7，16时段开行列车数量最少，均为4列。各个时段列车开行数量的分布情况如图4所示。其中，在非必停站，3站、4站、7站、8站停车次数分别为36，32，25和38次。从图4中不难发现，各时段列车开行数量分布与各时段的吸引度分布(图4中仅列出1站和5站的吸引度作为示例来说明。)总体保持波峰波谷趋势一致。但是又不完全符合旅客的对各出发时段的吸引度。主要有2个原因：第一，高峰时段由于拥挤会分流部分旅客；第二，不同出行时段对各车站旅客的吸引度不同。

表5 各时段的流量分配结果

图4 各时段列车开行数量

16个时段11种列车的分布情况，如图5所示。各类列车均有开行，能够服务沿途所有车站的旅客乘降，服务于各OD对的列车数量如表6所示，对于客流量较小的OD对，服务于该OD对的列车数量也相应较少，如OD对(3,4)、(4,7)等，从而降低了列车停站成本。但是各类列车的分布不均匀，如表7所示。其中，第3，8类列车开行数量最多，第10类列车开行数量最少。由于不同列车能够服务的OD客流是不同的，而不同OD客流量大小也有差异，这直接影响了优化后的列车开行方案。然而，不可否认的是，本文采用的启发式算法并不能完全寻找到最优解，因此，本算例计算的列车开行方案必然有等效方案。

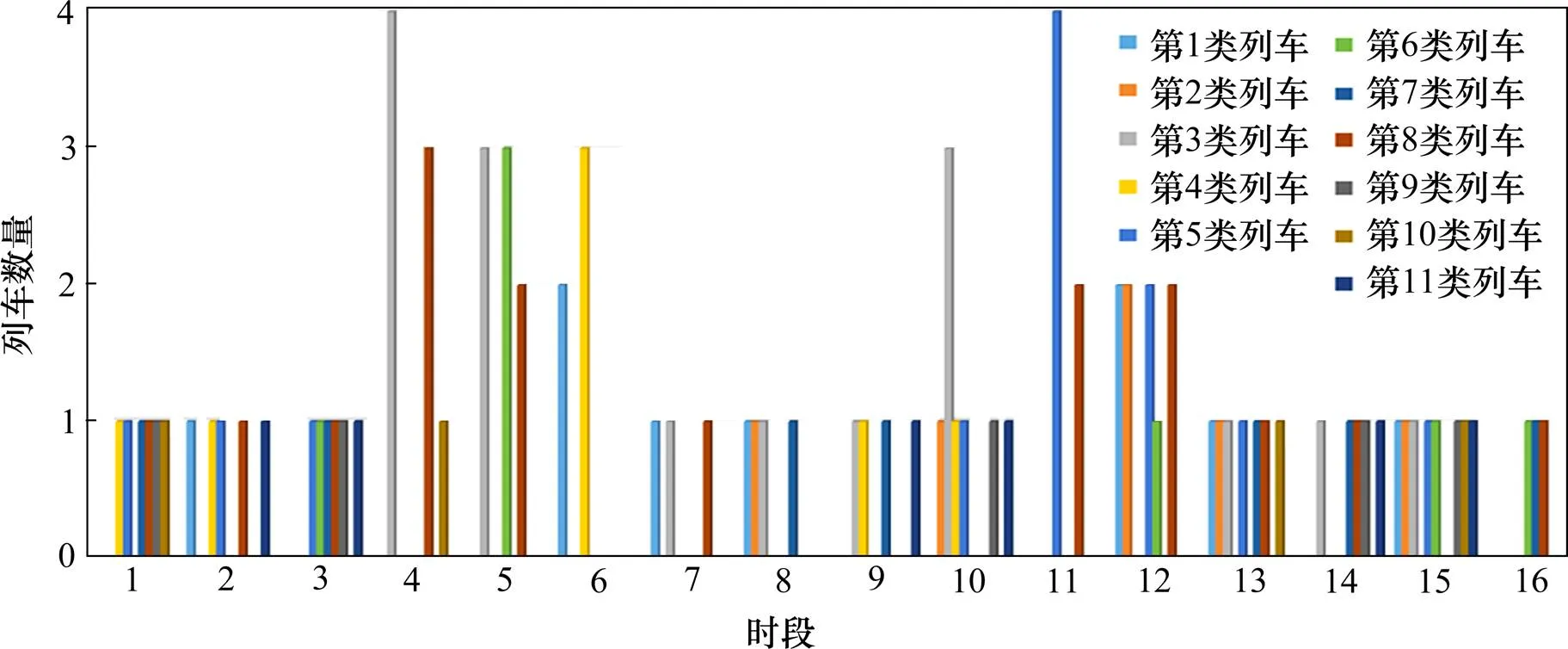
图5 各时段各种停站方案列车的开行数量

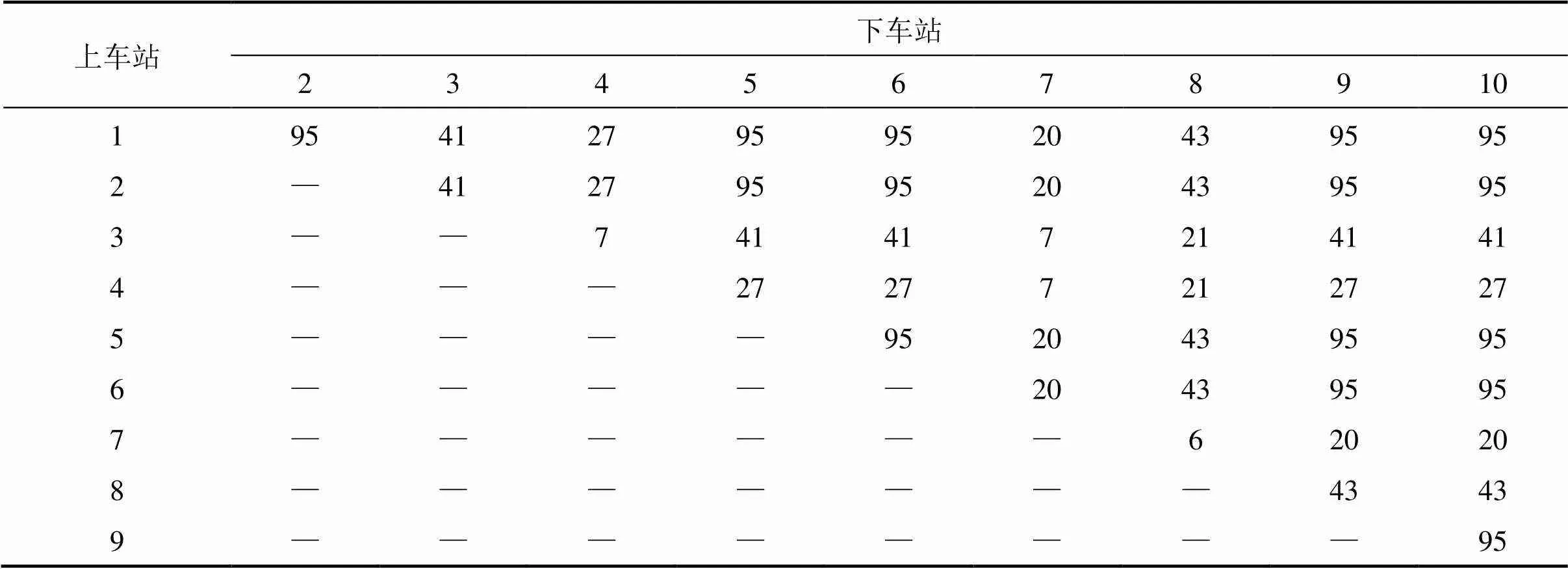
表6 服务于各OD客流的列车数量

在客流高峰时段，列车开行数量的最大值为9列，小于发车能力12列。本算例计算结果表明在客流高峰时段满负荷发车并不能完全满足所有旅客的出行需求，旅客并不会机械的完全按照出发时间吸引度的高峰时段出行，部分旅客会选择在低峰时段出行，应增加低峰时段的列车开行数量。

表7 不同停站方案列车的开行数量

4 结论

1) 旅客对出发时段的偏好性是一个动态平衡的过程，与客观的时段吸引度成正比，与动态的拥挤度成反比。

2) 不同车站的出行阻抗也是不同的，该值与各时段对旅客的吸引度相关。

3) 本文构建的双层规划模型能够描述旅客出行决策和高铁列车开行方案优化的动态博弈过程。 本文只研究了一个开行区段的高铁走廊，后续将研究多个运行区段的列车开行方案。

[1] YUE Y, WANG S, ZHOU L, et al. Optimizing train stopping patterns and schedules for high-speed passenger rail corridors[J]. Transportation Research Part C Emerging Technologies, 2016, 63(2): 126−146.

[2] LIN D, KU Y. Using genetic algorithms to optimize stopping patterns for passenger rail transportation[J]. Computer-aided Civil & Infrastructure Engineering, 2014, 29(4): 264−278.

[3] QI J, YANG L, DI Z, et al. Integrated optimization for train operation zone and stop plan with passenger distributions[J]. Transportation Research Part E Logistics & Transportation Review, 2018, 109: 151−173.

[4] Jens Parbo, Otto A Nielsen, Carlo G Prato. Reducing passengers’ travel time by optimising stopping patterns in a large-scale network: A case-study in the Copenhagen Region[J]. Transportation Research Part A Policy and Practice, 2018, 113: 197−212.

[5] SHANG Pan, LI Ruimin, LIU Zhiyong, et al. Equity- oriented skip-stopping schedule optimization in an oversaturated urban rail transit network[J]. Transportation Research Part C Emerging Technologies, 2018, 89: 321− 343.

[6] NIU H, ZHOU X, GAO R. Train scheduling for minimizing passenger waiting time with time-dependent demand and skip-stop patterns: Nonlinear integer programming models with linear constraints[J]. Transportation Research Part B, 2015, 76(jun.): 117−135.

[7] 李得伟, 韩宝明, 李晓娟, 等. 基于节点服务的高速铁路列车停站方案优化模型[J]. 铁道学报, 2013, 35(6): 1−5. LI Dewei, HAN Baoming, LI Xiaojuan, et al. High-speed railway stopping schedule optimization model based on node service[J]. Journal of the China Railway Society, 2013, 35(6): 1−5.

[8] 张小炳, 倪少权, 潘金山. 基于均衡性和可达性的高速铁路列车停站方案优化[J]. 计算机应用研究, 2017, 34(7): 1962−1965. ZHANG Xiaobing, NI Shaoquan, PAN Jinshan. Optimization of high speed railway stop schedule plan based on balance and accessibility[J]. Application Research of Computers, 2017, 34(7): 1962−1965.

[9] 牛丰, 戚建国, 秦进. 基于不确定客流的高速铁路列车停站方案优化方法[J]. 铁道学报, 2016, 38(7): 1−7. NIU Feng, QI Jianguo, QIN Jin. Optimization model for train stopping plan on high-speed railway corridor with uncertain passenger demands[J]. Journal of the China Railway Society, 2016, 38(7): 1−7.

[10] 黄志鹏. 基于旅行时间满意度的城际列车开行方案[J]. 兰州交通大学学报, 2018, 37(1): 27−32, 40. HUANG Zhipeng. Intercity Passenger Train operation based on travel time satisfaction[J]. Journal of Lanzhou Jiaotong University, 2018, 37(1): 27−32, 40.

[11] 赵杰群, 李夏苗, 苟敏. 基于区间数的高铁列车停站方案优化方法[J]. 铁道科学与工程学报, 2017，14(6): 24−30. ZHAO Jiequn, LI Xiamiao, GOU Min. Optimization of high-speed train stopping plan based on interval numbers [J]. Journal of Railway Science and Engineering, 2017, 14(6): 24−30.

[12] 刘璐, 孟令云, 李新毅, 等. 考虑旅客需求的停站方案与列车运行图一体化模型与算法[J]. 铁道科学与工程学报, 2019, 16(2): 518−527. LIU Lu, MENG Lingyun, LI Xinyi, et al. Integrated optimization of stopping pattern and train timetable for passenger demand[J]. Journal of Railway Science and Engineering, 2019, 16(2): 518−527.

[13] 邓连波, 史峰, 周文梁. 旅客列车停站设置方案优化[J]. 中国铁道科学, 2009, 30(4): 102−107. DENG Lianbo, SHI Feng, ZHOU Wenliang. Stop schedule plan optimization for passenger train[J]. China Railway Science, 2009, 30(4): 102−107.

[14] 龙品秀, 史峰, 胡心磊, 等. 不同需求日高铁列车开行方案协同优化方法[J]. 铁道科学与工程学报, 2019, 16(2): 310−318. LONG Pinxiu, SHI Feng, HU Xinlei, et al. The collaborative optimization of multi-day line plannings for high-speed railway[J]. Journal of Railway Science and Engineering, 2019, 16(2): 310−318.

[15] 陈路锋, 宋瑞, 何世伟, 等. 基于双层规划模型的高速铁路列车开行方案优化研究[J]. 铁道运输与经济, 2013, 35(6): 18−23. CHEN Lufeng, SONG Rui, HE Shiwei, et al. Study on optimization of high-speed railway train working diagram based on bi-level programming model[J]. Railway Transport and Economy, 2013, 35(6): 18−23.

[16] HUANG Z, NIU H. A bilevel programming model to optimize train operation based on satisfaction for an intercity rail line[J]. Discrete Dynamics in Nature and Society, 2014, 2014(2): 1−7.

[17] Wardrop J G. Some theoretical aspects of road traffic research[C]// Proc Inst Civ Eng, 1952, Part II: 325−378.

A bi-level programming approach of period-preferred train operations for high-speed railways

HUANG Zhipeng1, TIAN Zhiqiang1, SI Xiaoxin2

(1. School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. Lanzhou Railway Station Operation Depot, China Railway Lanzhou Group Co., Ltd., Lanzhou 730050, China)

There are a few trains running parallelly on a congested high-speed railway corridor at different periods daily. Hence passengers can choose freely among them. Their preference of departing period choice is the main factor determining the distribution of passenger demands. The objective of this paper was to meet, to the maximum extent possible, the passengers’ preference demands of departing periods and to work out reasonable train stopping operations to avoid congestion. Firstly, two vital affecting factors, attractivity and congestion, were analyzed. Meanwhile, the passenger travel impedance function was established, and a bi-level programming model was constructed. The upper integer planning model regarded the minimum operation cost as the goal to decide train stopping operations and its running frequency. The lower model was a user-equilibrium one aimed at distributing passenger flows scheme based on the optimal train stopping operation. Finally, a heuristic algorithm embedded with Frank-Wolfe algorithm was designed based on model characteristics, and a simulation calculation was carried outto verify both the model and the algorithm.

high-speed rail; train stopping operation; bi-level programming model; user equilibrium; heuristic algorithm

10.19713/j.cnki.43−1423/u.T20200562

U293.1

A

1672 − 7029(2021)04 − 0861 − 08

2020−06−19

国家自然科学基金资助项目(71761023)；甘肃省自然科学基金资助项目(18JR3RA110)

黄志鹏(1983−)，男，河南长葛人，副教授，博士，从事交通运输规划与管理研究；E−mail：huangzp@mail.lzjtu.cn

(编辑 阳丽霞)