考虑交通拥堵的车辆路径优化模型及改进蚁群算法求解

王 安,向万里*,王璐璐,杨 亮

(1. 兰州交通大学 交通运输学院,甘肃 兰州 730070;2. 兰州交通大学 现代物流研究所,甘肃 兰州 730070)

0 引言

物流配送中的车辆路径问题[1]一直受学者重视,李阳[2]、张晓楠[3]和张海军[4]分别用改进生物共栖搜索算法、改进分散搜索算法和改进蚁群算法对车辆路径问题求解,通过优化算法得到更可靠的寻优能力.经典车辆路径问题往往设定车辆行驶速度恒定,而李兵飞[5]重点考虑车辆路径问题中配送车辆在不确定条件下的速度变化,并且设计改进人工蜂群算法对模型求解.很多学者从节能减排的角度出发对车辆路径问题进行延伸,Demir Emrah[6]、Xiao[7]、李进[8]、Zhang[9]、何东东[10]以及葛显龙[11]研究绿色物流,从低碳环保的角度考虑配送过程中车辆的耗油量和碳排放,并设计相应算法对其进行研究.针对城市物流配送下的车辆路径问题,Wang[12]在两级配送下研究需求可拆分的城市物流配送问题,用遗传算法寻求减少配送成本得到很好的解决方案;葛显龙[13]在城市配送中考虑动态需求下车辆路径优化问题取得有效的成果;Milena Janjevic[14]对多级配送网络中最后一英里的供应策略进行研究,对末端物流做了详细的分析.对于道路拥堵对配送的影响,姚坤[15]单对上海市道路交通拥堵指数表示交通拥堵程度,用粒子群算法分时间段研究拥堵对碳排放的影响,通过牺牲配送时间减少碳排放量;赵志学[16]研究交通拥堵对冷链物流运营成本的影响,通过分析拥堵对经济成本、环境成本的影响,运用蚁群算法求解得到减少成本的优化方案,提出在冷链运输中规避拥堵时段达到减少配送成本、环境污染的目的.王来军[17]研究城市交通网络中选址问题和配送问题,考虑交通拥堵并基于MapGIS二次开发实现交通网络优化,以此为基础进行可视化.

综上所述,现有的研究已经为考虑交通拥堵车辆路径问题奠定了良好的基础,但由于问题本身的复杂性和实际情况中影响因素的多样性,也存在一定的局限性.现有物流配送中考虑交通拥堵状况的文献较少,并且物流配送中拥堵对配送时间的影响没有符合我国城市交通特性较可靠的转化方法.因此,本文建立交通拥堵状态下的车辆路径优化模型,设计改进蚁群算法优化配送路线,缩减配送时间,并通过案例验证模型和算法的可行性,最后通过百度地图规划实际配送路线.

1 模型建立

1.1 问题描述

本文研究的基于交通拥堵状况下车辆路径规划问题可以描述为:1个配送中心,1组相同容量的车辆K=(1,2,…,N)对多个客户C=(1,2,…,M)完成配送任务,车辆的最大容量为W,客户分散在交通网络中,客户与客户之间可能存在多条路线,每个客户有且仅由1辆车对其进行配送.车辆因为拥堵影响行驶速度,进而影响车辆的行驶时间.以所需车辆数最少和配送时间最短为目标进行求解.

1.2 前提假设

交通网络G是强连通图,G=(V,E)由1组节点V={0,1,…,n}和1组连接V的路段E∈V×V组成.C⊂V是分布在G中的客户,每条路段E可能发生拥堵.配送中心有足够的车辆数完成配送任务,不考虑车辆装卸时间.

1.3 行驶时间

针对拥堵路段,为了有效刻画交通拥堵下实际路段行驶时间,采用交通部组织的国家“九五”交通科技重点攻关项目“公路通行能力研究”中,结合我国公路交通特性修正后的模型得到时间阻抗函数如式(1).式(1)中I是对交通服务水平的评价,用来反映拥堵状况(见表1),其中参数取值[18]α1=1.5，α2=1.88，α3=7.当已知某一路段的长度d、自由流车速v、拥堵状况I时,可以通过式(1～2)计算车辆在路段上的行驶时间t,模型参数见表2.

(1)

(2)

表1 道路服务水平

表2 模型参数

1.4 数学模型

在交通拥堵状态下,为反映城市道路拥堵对物流配送的影响,基于我国道路交通特性计算配送车辆行驶时间的方法,构建交通拥堵状态下的车辆路径优化模型.

(3)

(4)

目标函数为

N=minK，

(5)

(6)

约束条件:

(7)

(8)

(9)

(10)

yck=0或1,∀c∈C,∀k∈K,

(11)

∀(i,j)∈E,且i≠j,

(12)

dij>0,Iij>0,且i≠j.

(13)

式(5)表示完成配送所需车辆数最少函数,式(6)表示交通拥堵状态下完成配送的所有车辆行驶时间最短函数,式(7)表示每个客户有且仅由一辆车对其进行配送,式(8)表示配送车辆所载的物品不得超过它的最大荷载,式(9)表示车辆从配送中心出发后,最后必须回到配送中心,式(10)到式(13)表示变量的取值范围和非负约束.

2 改进蚁群算法设计

蚁群算法[19]是模拟蚂蚁在觅食过程中发现最短路径的智能算法.基本思想是蚂蚁在寻优过程中根据自身的选择和其它蚂蚁释放的信息素浓度[20]逐渐靠近最优解.优点在于本质上是并行算法,个体之间靠信息素传递信息,引导蚁群逐渐搜索靠近最优解,收敛速度快,鲁棒性强.缺点在于受信息素影响极易陷入局部最优,转移规则[21]比较依赖距离较近的点,为了避免陷入局部最优加快搜索最优解的速度提出了改进的蚁群算法,改进的蚁群算法如下.

2.1 编码方式

编码方式采用自然数编码,对交通网络中所有的节点进行标号,任意客户所在的节点产生的排列都是可行解,解码时从第一个客户节点起,依次添加直到第n个客户的需求超出运输车辆的荷载,将1～n-1的客户作为1辆车的配送.假设产生的编码1～9是需要配送的客户节点,0是配送中心,按照上述解码思想,第一辆车从编码的第一位客户1开始装入直到客户5的需求超出车辆的荷载,得到第一辆车的客户集合以及配送顺序:0-1-2-3-4-0,第二辆车从客户5开始装入直到客户8的需求超出车辆的荷载,得到第二辆车的客户集合以及配送顺序:0-5-6-7-0,第三辆车从客户8开始装入直到客户9的需求没有超出车辆的荷载且没有其它需要配送的客户,得到第三辆车的客户集合以及配送顺序:0-8-9-0.

2.2 转移规则改进

转移规则[22]的设计考虑到加快收敛速度,转移概率由式(14)决定,引进1个随机变量p和1个常量q(p∈(0,1)，q∈(0，1)),本文取q=0.2,客户节点i对下一个客户节点j的选取采用确定性选取和轮盘赌选取,选取方式依据式(15～17).

(14)

(15)

(16)

(17)

式中：pij是节点i到节点j的转移概率;τij是节点i到节点j上信息素浓度;ηij是节点i到节点j的吸引程度,考虑先验信息对搜索的引导,节点i到节点j的选取不但需要距离相近最终还要考虑回归到初始点,综合考虑相近性和回归性引入节约距离wij=di0+dj0-dij,ηij的计算方法如式(16);考虑道路拥堵对道路服务水平的影响引入μij,μij是节点i到节点j的拥堵影响,μij的计算方法如式(17);J(i)是除了已经配送的客户剩下其它需要配送客户的集合；α为信息启发式因子；β为期望启发因子；γ为交通拥堵因子,本文中α=γ=1,β=5.

2.3 信息素更新规则改进

为了解决当所有蚂蚁参与更新时,大多数节点信息素浓度会大范围提高,没有突出较优蚂蚁的吸引能力,因此信息素的更新采取用每一代中的精英蚂蚁更新相应路段上的信息素,当本代中所有蚂蚁完成一次循环后,选出本代最优的蚂蚁个体m,把上一时刻的信息素τij(t)更新为τij(t+1),具体更新规则如式(18～19).

(18)

(19)

2.4 局部搜索方式改进

由于蚂蚁个体解路径由转移规则决定,解路径的质量需要优化,为了改进蚁群算法提高算法中解的质量,本文对蚁群算法产生的优质解采用禁忌搜索算法的思想进行局部搜索,即生成一组可以交换的位置,位置之间互相不重复,所有位置交换后对得到的可行解评价并记录交换的位置,评价由高到低排序,跟蚁群算法本代中产生的最优解比较,记录并评价比本代最优解用时少的所有交换位置,依次对记录下的交换位置进行交换,选择最优值作为本代最优的蚂蚁个体,对信息素再一次更新.

2.5 终止规则改进

算法不采用通过限定迭代次数的方式终止,而是采取蚁群长时间无法探索更优解时进行终止,具体指每一代的蚂蚁群体选取最优蚂蚁个体作为当代最优解,直到后代中无法搜索出比历代最优个体更优的次数达到设定的期望值limit,算法终止,具体改进蚁群算法流程如图1所示.

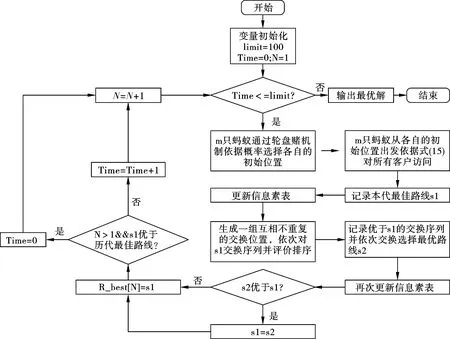
图1 改进后蚁群算法流程

3 算例验证和结果分析

实验1采用公共标准算例,对改进的蚁群算法进行验证,算例来源https://neo.lcc.uma.es/vrp/vrp-instances/capacitated-vrp-instances/.实验2考虑交通拥堵状态下车辆路径问题,针对兰州市某公司配送业务以兰州市为背景在兰州市七里河区、安宁区、城关区、新区等地选取27个备选点,通过调用百度地图得到备选点的经、纬度,将其标注到地图里,画出备选点所在路网并标记出每个路段号.算法采用Matlab R2018a编程,在CPU 2.10 GHz内存为4 GB电脑上运行.

实验1取文献[23]采用的7个算例,表3是10次实验与文献[23]对比的结果.结果显示本文算法在7个算例中有6个找到了最优值,并且6个算例的最优值、最差值和平均值均相同且优于文献[23]算法.

表3 实验1的比较结果

实验2从27个备选点里随机选取17个点作为配送中心和客户所在位置，如图2所示.配送中心和客户分布的具体数据信息如表4所示.

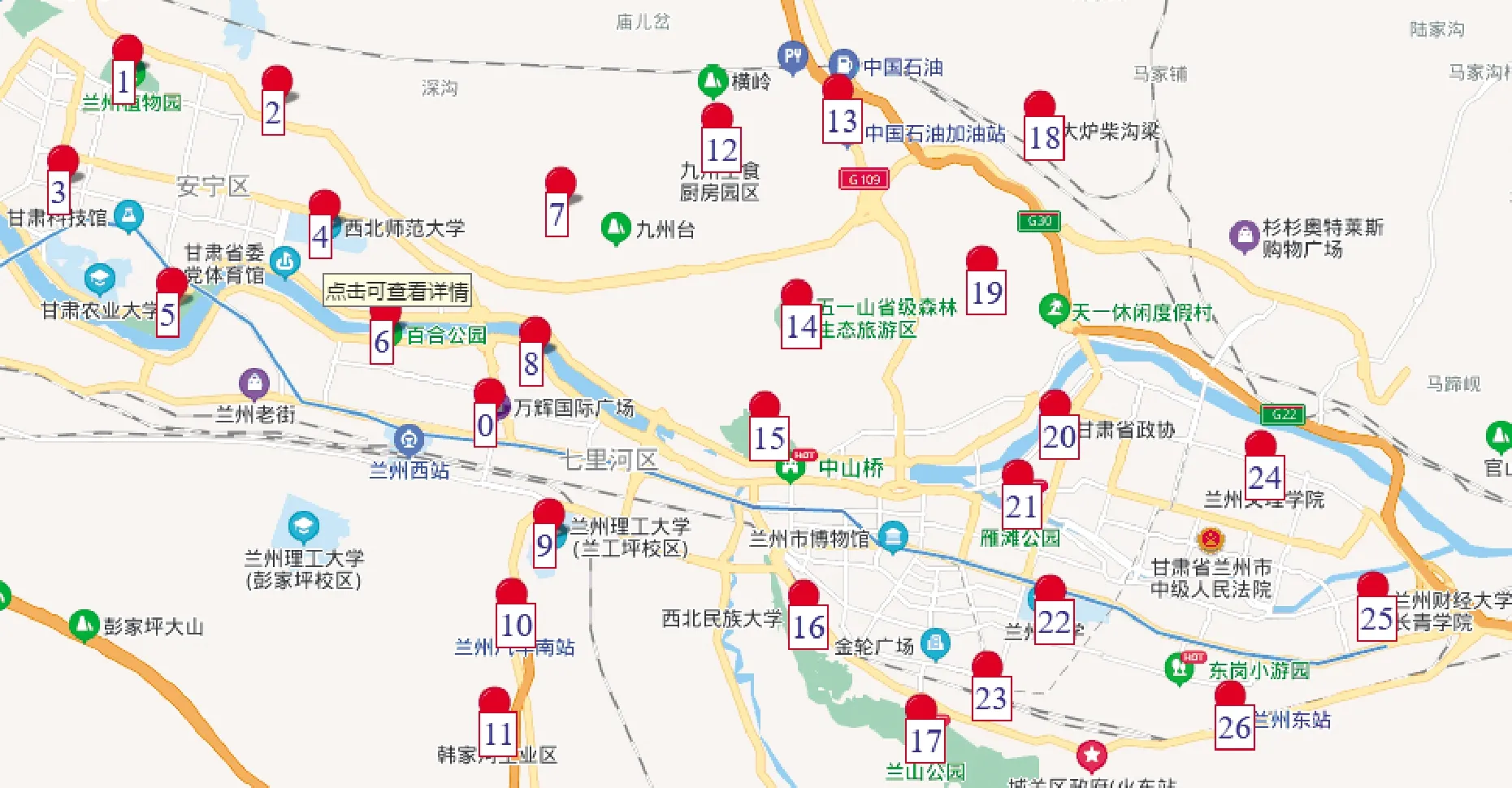
图2 配送中心以及客户的分布

表4 客户分布的具体数据信息

路网尽可能的靠近百度地图中实际的分布,路网中的节点和路段符合强连通图的要求,路网如图3所示(路段标记数字是路段号),路段往返两个方向上的I大小不一定相等,路段的长度根据客户的经纬度得到直线距离按1∶100比例扩大,路段信息如表5所示.

图3 路网分布

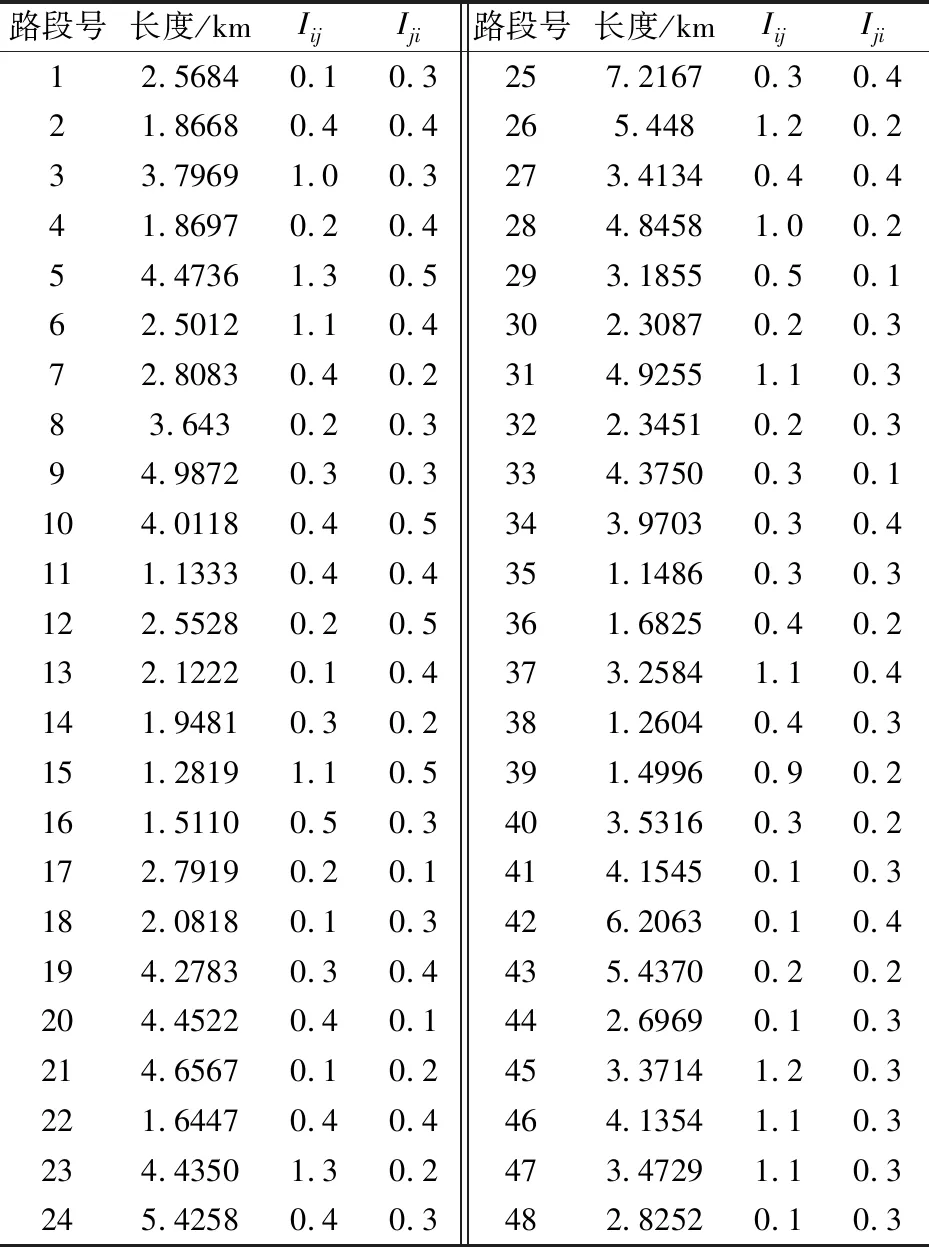
表5 路段信息

实验2以车辆数最少和配送时间最少作为优化目标,运用改进蚁群算法对目标求解.算例中客户是: 2、3、5、8、9、10、12、14、15、16、18、20、22、23、24、26,在拥堵状态下求解配送方案如图4所示.配送车辆数为3,配送时间为128.921 9 min,第一辆车对客户9、14、16、20、22、23、24、26配送,行车路线为:0—8—14—19—20—24—25—26—22—23—16—9—0;第二辆车对客户2、3、5、8、10配送,行车路线为:0—8—6—5—3—2—7—8—0—9—10—9—0;第三辆车对客户12、15、18配送,行车路线为:0—8—7—12—13—18—14—15—0.

图4 拥堵状态下的配送方案

保持客户,车辆,路网,拥堵信息一致,在当前拥堵路段进行配送,记录实际行驶路线和行驶时间,跟所提研究方案中路线所花费的时间、距离进行比较,见表6.

通过表6分析可知,配送中心为完成对16个客户的配送安排了3辆车,总体来看,从路线1、2、3可以看出算法在拥堵路段的替代路径距离虽然较长但实际行驶时间较短时,选用替代路径,减少配送时间;从线路2的前半段可以看出算法在拥堵路段的替代路径距离较长且行驶时间较长时,依然继续使用当前拥堵路段.尽管拥堵状态下优化后的运行方案更换了线路增加配送车辆行驶距离,但是大大缩减配送车辆的配送时间,减少因拥堵等待耗费的时间,提高配送中心的配送效率.这表明,所提研究方案在交通拥堵状态下车辆路径的选取是可行的.

表6 实验2方案对比表

4 结语

交通拥堵状态下车辆路径规划问题中,考虑到选用替代路段代替拥堵路段减少配送时间,构建交通拥堵下的车辆路径优化模型,采用改进的蚁群算法对模型进行求解,最后采用算例验证模型的有效性和算法的可行性.实验结果分析发现计改进后的蚁群算法寻优能力更强稳定性更高;在交通拥堵状态下,优化后的方案在拥堵路段的替代路径距离虽然较长但实际行驶时间较短时,很好地选用替代路径,减少配送时间;在拥堵路段的替代路径距离较长且行驶时间较长时,依然继续使用当前拥堵路段,缩减配送时间增加客户满意度,但配送行驶距离增加幅度不高.因此,可以在实际应用中对拥堵状态下物流企业配送方案提供方法支持和参考.