基于稀疏混沌多项式的边坡可靠度分析方法

缑变彩, 王 帆

(1. 武汉科技大学城市学院 城建学部, 湖北 武汉 430083； 2. 华中科技大学 土木与水利工程学院， 湖北 武汉 430074)

土体作为典型的天然材料具有非匀质性、各向异性，呈现出空间变异特征，而土的工程特性依赖于土体的空间平均特性，因此在进行岩土结构变形与稳定性分析时需要考虑土体参数的空间变异性对分析结果的影响[1]。边坡作为典型的岩土结构在进行稳定性分析时也需要对土体参数的空间变异性进行充分模拟。

当前针对空间变异土体的边坡稳定性问题国内外已有诸多研究成果[2～5]，其中分析的重点和难点主要体现在两个方面，即土体参数空间变异性的模拟和边坡失稳概率的高效计算。土体参数的空间变异模拟通常基于随机场理论，通过均值函数、方差函数等描述拓扑空间中任意一点的随机特性，通过自相关函数描述拓扑空间中任意两点之间的相似性[6]。随机场离散是实现土体参数空间变异性模拟的关键步骤之一，目前常用的离散方法可分为空间离散法和级数展开法[7]。空间离散法包括中点法、形函数法、局部平均法等，空间离散法的误差精度与随机场网格划分有关，对于自相关长度较小的情况需要较为精细的随机场网格，导致计算效率较低。级数展开法是将随机场表示为级数展开形式，通过截断展开项近似表达原有随机场。Karhunen-Loève(K-L)级数展开是其中较常用的一种，相较于其他方法，K-L法从随机场离散误差和离散后输入变量空间维度的角度讲是最优的[8,9]，因此在边坡可靠性分析中广泛用于土性空间变异性模拟。

边坡稳定性分析方法包括极限平衡法、有限元法和极限分析法等，采用一阶/二阶可靠度、点估计、蒙特卡洛等方法估计边坡失稳概率[10～12]。然而这些方法一般需要进行多次稳定性分析，尤其是稳定性分析模型较复杂(如有限元)或小概率问题时计算效率较低。针对这一问题，采用代理模型是一种有效的解决办法，即通过实验设计进行有限次数的分析获取输入输出样本，再通过训练学习得到新模型并用于可靠度分析。常用代理模型包括二次响应面、克里金法、人工神经网络等[13,14]。其中多项式混沌展开(Polynomial Chaos Expansion，PCE)因其严格的数学背景，可表达任意有限方差随机响应，且对于平滑的输入输出关系收敛迅速，因此得到广泛应用。该方法的应用可分为侵入式和非侵入式两种，如采用随机伽辽金法求解PCE系数的谱随机有限元属于侵入式方法[15]，而采用随机配点法求解PCE系数则属于非侵入式方法[16]。通常而言，侵入式方法(如随机伽辽金法)相比非侵入式方法(如随机配点法)精度更高，但由于需要对原计算模型进行修改，使用过程较为复杂，甚至对于某些复杂非线性系统其对应的PCE方程难以推导；而非侵入式PCE模型的构建与求解与原计算模型是解耦合的，因此适用范围更广。考虑土性空间变异的边坡稳定性分析属于典型的非线性问题，且输入空间维度较高，而PCE展开项和未知系数的个数会随PCE阶数和输入空间维度的增加迅速增长，导致系数求解所需要的原有模型计算成本过高。

为解决这一问题，Blatman[17]提出了一种基于稀疏多项式混沌展开(sparse PCE，sPCE)的代理模型方法。该方法利用稀疏效应准则，采用压缩感知算法重构稀疏的展开式，即非零系数项，运用基于留一误差的回归算法求解有限的展开式系数，实现了求解精度与计算效率之间的平衡。本研究采用sPCE方法评估土性空间变异边坡的失稳概率，分析不同输入变量的全局敏感度。为实现这一目标，采用PCE逼近理论构造边坡稳定性代理模型，利用正交匹配追踪[18]实现PCE稀疏化重构，结合拉丁超立方抽样建立目标精度下的PCE系数自适应求解[19]。该方法分别用于分析不同随机场模型和边坡稳定性计算模型的边坡失稳概率，为高效评估边坡可靠性提供思路。

1 土性随机场离散的K-L法

设H(z)是一随机场，z∈Ω是d维拓扑空间Ω⊂Rd中的一点。另设随机场均值函数为μ(z)，自协方差函数为C(z,z′)，则该随机场可展开为如下表达式：

(1)

式中：ξi为一系列零均值、单位方差且不相关的随机变量；λi和φi(z)分别为自协方差函数的特征值和特征函数，即求解如下广义特征值问题：

(2)

为便于计算，需要对K-L级数进行截断，仅保留有限项特征值及特征函数来近似表达原随机场，其对应的均方误差为：

(3)

通常需要对特征值从大到小进行排序，取前m项从而使得在允许误差下K-L级数展开项数最少。

对于高斯随机场，ξi为独立标准高斯随机变量；而对于非高斯随机场，ξi通常难以获得。因此K-L级数展开主要用于表达高斯随机场，而对于非高斯随机场则采用场转换理论将K-L级数展开表达的高斯场转换为对应的非高斯场。由于土性参数如抗剪强度通常是非负的，理论上不适合采用高斯场模拟，因此实际中常假设为对数正态随机场，并采用下式进行转换：

HLognormal(z)=exp(HGauss(z))

(4)

2 稀疏多项式混沌展开方法

2.1 多项式混沌展开

PCE逼近理论的基本思想是用一组正交多项式之和近似表达概率空间中的隐式函数。设响应量y与n维独立随机变量x=[x1,x2…,xn]之间存在某函数关系y=f(x)，则y可以展开为一组正交基函数：

(5)

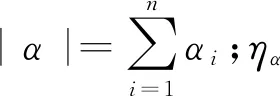
=γαδαβ

(6)

2.2 展开式系数求解

建立PCE代理模型的关键在于展开式系数求解。为便于计算，需要对展开式进行截断，取最大阶数p以内的展开项，即|α|≤p对应的基函数。对于非侵入式模型构建，常用的系数求解方法有投影法、配点法、回归法等。相较而言，在调用相同原计算模型次数的情况下，回归法的收敛速度更快，因此这里采用回归法进行求解。首先通过实验设计得到输入空间内的一组样本X=[x(1),x(2),…,x(N)]T，然后调用原计算模型得到对应的响应量Y=[y(1),y(2),…,y(N)]T，则展开式系数为：

ηα=(ΨTΨ)-1ΨTY

(7)

若对于n维输入变量采用p阶PCE拟合其响应关系，则展开项总项数P为：

(8)

可以看到PCE展开总项数随着输入空间维度和PCE阶数快速增长，而实际中为确保系数求解的精度，通常实验设计采样次数需要k≥2P，因此对于高维问题或高阶PCE展开则会导致原模型计算次数显著增加。在某些情况下，即使采用K-L级数展开表达随机场，其输入变量维度也较高，例如土性空间变异性通常采用在原点处不可微的指数型自相关函数，且在垂直方向上的自相关长度较小，从而导致离散误差收敛速度较慢，需要较多的独立标准高斯随机变量去近似表达离散随机场模型。因此需要采用更有效的方法估计PCE展开式系数。

2.3 正交多项式基函数的稀疏化选取

根据稀疏效应准则，实际问题中占主导的展开式通常是仅包含单独输入变量的多项式基函数和变量之间的低阶交叉项，而其他多项式对应的系数趋近于零，对结果影响较小，可以忽略。因此，可以通过合理选取多项式基函数提高PCE模型建立的效率。

基函数选取的关键在于如何确保所构建的代理模型其泛化误差是足够小的。采用训练误差判断模型精度容易造成过拟合现象，因此不适宜作为选择标准。为解决这一问题，通常采用交叉检验的方法进行误差判断。特别地，当交叉检验每次仅选取一个样本作为验证集则对应留一法(Leave-one-out，LOO)，相应的LOO误差为：

(9)

(10)

式中：hi是矩阵Ψ(ΨTΨ)-1ΨT的第i个对角元素。

上述LOO误差为基函数的选取提供了一种有效的评价指标。常用的基函数选取方法包括贪心算法和凸松弛算法等，其中贪心算法给出的是L0范数(非零PCE系数的个数)最小化问题的近似解，而凸松弛算法则是将上述L0范数最小化问题转化为L1范数(各PCE系数绝对值之和)最小化问题后求解[20]。本文采用贪心算法中的正交匹配追踪算法进行重要基函数的选取[21]，该算法通过不断验证残差和备选基函数之间的正交性确定最似非零系数的基函数，然后再以式(7)求解当前选取的基函数对应的展开项系数。具体算法如下：

(3)更新已选基函数集Ak=Ak-1∪jk和候选基函数集Ck=Ck-1jk。

(4)用式(7)求解当前已选基函数Ψα,k={Ψαj}j∈Ak的系数ηα,k，并更新残差rk=Y-Ψα,kηα,k。

(5)用式(9)计算当前PCE代理模型的LOO误差εLOO,k。

(6)重复(2)～(5)直至k=min(N,P)。

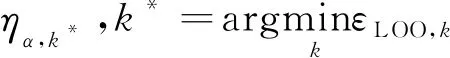
3 考虑土性空间变异的边坡可靠度与全局敏感性分析

基于上述K-L级数展开和sPCE代理模型可实现土性空间变异的边坡可靠度高效评估，并分析不同变量的全局敏感性。具体流程如图1所示。

图1 分析流程

(2)对土性随机场进行K-L分解，求得截断误差内的K-L表达。

(3)采用拉丁超立方抽样获取实验设计样本。

(4)建立边坡稳定性计算模型，计算样本对应的边坡安全系数。

(5)通过正交匹配追踪选取多项式基函数。

(7)依据构建的sPCE代理模型，采用蒙特卡洛法估计边坡失稳概率；计算不同输入变量的Sobol指数STi：

(11)

4 算例分析

4.1 一维随机场

图2 边坡示意/m

图2为某1∶2边坡，设土体不排水抗剪强度随深度方向的空间变异性可用平稳对数正态随机场Su(z)模拟，均值为40 kPa，标准差为10 kPa，自相关函数为ρ(z,z′)=exp(-|z-z′|/l)，l=3 m为自相关长度，土体重度为γ=18 kN/m3。边坡稳定性计算常采用极限平衡法或有限元法。考虑到边坡失效概率较小，采用有限元法验证时计算成本较高，故此处边坡稳定性计算采用极限平衡法中的Bishop法，滑移面假设为圆弧型。由于本文提出的sPCE代理模型构建属于非侵入式方法，因此将极限平衡法替换为有限元法构建sPCE代理模型也是完全可行的。

设K-L截断允许误差为5%，则需要前21阶特征值和特征函数。允许的LOO误差设为1×10-8，初始实验设计样本大小和每次扩充样本大小均为20。

图3给出了sPCE代理模型构建的LOO误差演化，经过11次迭代降低到允许误差范围内。图4给出了该误差下构建的sPCE模型在训练集上的结果对比。

图3 LOO误差变化

图4 sPCE模型在训练集上的结果对比

为验证模型的有效性，以蒙特卡洛仿真(Monte Carlo Simulation，MCS)50000次的原模型计算结果作为参考，失效概率为9×10-4，估计误差为±14.9%。图5给出了基于构建的sPCE模型预测结果与实际计算值的对比。图6给出了两种方法求得的边坡安全系数的概率密度函数，基于sPCE模型求得的边坡安全系数的分布与MCS方法一致。然而MCS方法共调用原边坡稳定性分析模型5万次，耗时约4 h，而采用sPCE方法仅调用了220次。另外，建立的代理模型仅包含218项多项式基函数，仅为完整PCE展开项数的0.07%。

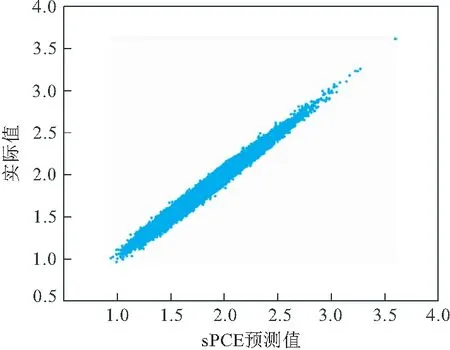
图5 sPCE模型在测试集上的结果对比

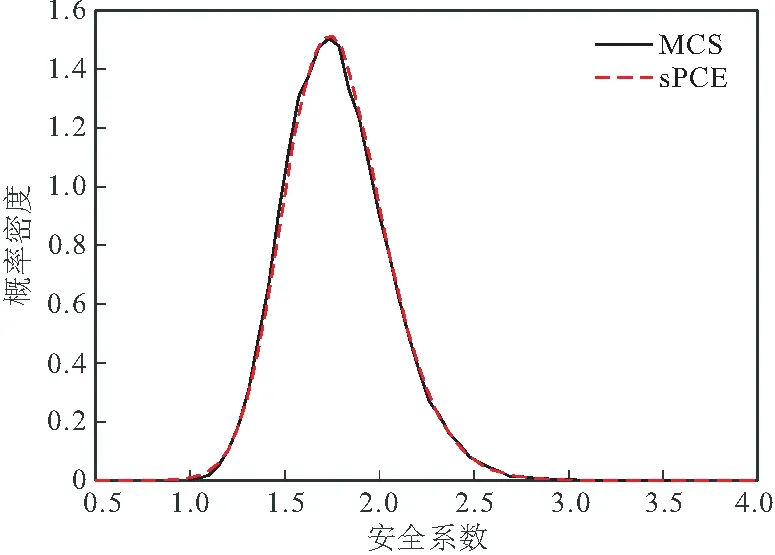
图6 边坡安全系数概率密度函数对比(算例1)

基于sPCE模型可以高效地计算安全系数的统计矩和失效概率。表1给出了不同允许误差下安全系数的均值与方差，可以看到，随着允许误差的降低，需要更高阶的PCE展开项来减小拟合误差，相应地模型给出的统计量和失效概率逐渐逼近MCS方法得到的结果，模型精度随LOO允许误差的降低而上升。

表1 不同允许误差下的可靠性分析结果(算例1)

图7给出了不同输入变量的全局敏感性，且Sobol指数的总和略大于1，可见不同特征模式的交互项对全局敏感性影响较小。影响边坡安全系数变化的主要是前4阶特征模式，图8给出了前4阶模式的特征值及其特征函数。可以看到，由于边坡安全系数取决于土体的空间平均特性，因此对于不排水抗剪强度在局部的空间变化(即高阶特征模式)并不敏感。

图7 不排水抗剪强度参数空间变异特征模式的敏感性

图8 前4阶特征值和特征函数

4.2 二维随机场

设K-L截断允许误差为5%，则需要前82阶特征值和特征函数。允许的LOO误差设为1×10-8，初始实验设计样本大小和每次扩充样本大小均为10。该问题属于典型的高维建模，对于4阶sPCE模型，备选基函数的数目高达212万，因此从完整的sPCE展开基函数中进行选取效率十分低下。因此基于稀疏效应原则，仅将包含单变量的基函数及包含两个不同变量的低阶交互项作为备选基函数，使得相应的备选基函数数量降低至3650项。

表2给出了不同允许误差下的分析结果，在允许误差为1×10-8时需要构建4阶模型来达到设定的误差范围，失效概率估计为5.8×10-2。为验证模型的准确性，将代理模型得到的边坡安全系数的分布与1000次蒙特卡洛仿真结果进行比较，从图10可以看到两者基本一致，蒙特卡洛方法估计的失效概率为6.0×10-2，估计误差为±12.5%。

图10 边坡安全系数概率密度函数对比(算例2)

表2 不同允许误差下的可靠性分析结果(算例2)

图11给出了不同输入变量的全局敏感性， Sobol指数的总和约等于1，说明不同特征模式的交互项对全局敏感性影响可以忽略。影响边坡安全系数变化的主要是前2阶特征模式，而对高阶特征模式并不敏感，图12给出了对应的特征值及其特征函数。

图11 不排水抗剪强度参数空间变异特征模式的敏感性

图12 前2阶特征值和特征函数

5 结 论

考虑边坡土性空间变异性时输入空间维度通常较高，采用多项式混沌展开逼近理论拟合响应量其多项式基函数会快速增长，给代理模型的建立提出了挑战。采用正交匹配追踪算法可以自动选择重要的基函数，实现模型稀疏化构建，减少原计算模型的调用次数。

边坡可靠性分析算例表明，对于K-L离散土性随机场带来的高维输入空间问题，仅需较少次调用原边坡稳定性分析模型，即可得到较为精确的边坡安全系数概率分布及其统计矩，构建的代理模型中非零系数多项式基函数远小于完整多项式混沌展开的项数，且主要是仅包含单变量的基函数及包含两个不同变量的低阶交互项，大量的高阶交互项对拟合边坡安全系数并没起到作用。

全局敏感性分析表明，由于边坡安全系数取决于土体的空间平均特性，因此影响边坡安全系数变化的主要是低阶特征模式，而对于高阶特征模式并不敏感，因此在构建边坡稳定性分析的多项式混沌展开代理模型时还可以进一步简化，对于K-L展开仅截取其低阶特征值和特征函数。