有限数据条件下土性参数波动范围计算方法的有效性分析

田 密， 盛小涛

(1. 湖北工业大学 土木建筑与环境学院， 湖北 武汉 430068； 2. 武汉大学 水工岩石力学教育部重点实验室， 湖北 武汉 430072；3. 长江科学院 水利部岩土力学与工程重点实验室， 湖北 武汉 430010)

自然界土体因受复杂地质成因影响呈现出显著的空间变异性[1]。20世纪70年代，Vanmarcke提出土体剖面的随机场模型，提出用波动范围反映空间两点间土性参数的相关性。在波动范围内，土性参数是相关的，大于该范围可认为基本不相关[2]。波动范围是联系点变异性和空间平均特性的重要纽带，也是随机场模型应用于实际工程的一个重要参数[2～4]。因此，如何准确地计算波动范围是应用随机场模型恰当描述土性参数空间变异性的关键。

目前，在求解波动范围方面国内外学者做了大量工作，现有波动范围计算方法主要有平均零跨法[1]、递推空间法[1]、相关函数法[5]、拟合方差折减函数法[6]以及回归模拟法[7]等。近些年也有学者提出了确定土性参数统计特征值(如波动范围)的贝叶斯方法[8～10]。虽然现有波动范围计算方法较多，但不同方法的理论根据、可靠性和应用难易程度各不相同。如我国学者闫澍旺等[11]利用各种方法对大量实测的静力触探锥尖阻力和侧摩阻力数据进行分析，得到递推空间法、相关函数法及平均零跨法计算结果相差不多，计算结果可信程度比较高。程强等[12]通过数百个土层静力触探资料的计算得到递推空间法和相关函数法是稳定可靠的计算方法，平均零跨法和回归模拟法使用有其局限性，计算结果常有较大偏差。李小勇和谢康和[8]利用各种方法对太原工程场地粉质粘土层比贯入阻力进行了波动范围的计算分析，统计模拟法计算结果明显偏大，且变异性大，计算结果的稳定性差，而递推空间法、相关函数法以及平均零跨法等方法计算结果相差不多，结果可信度比较高。李镜培等[13]采用递推空间法和相关函数法分析了静力触探比贯入阻力实测数据，得出递推空间法与相关函数法的求解结果相当接近的结论，建议在大量工程场地的波动范围计算时采用递推空间法。谭晓慧等[14]根据安徽省某工程场地的粉质粘土层6个静探孔数据资料对求波动范围的相关函数法和递推空间法进行了对比研究。

现有波动范围计算方法准确性与可靠性的对比研究主要基于工程实测数据。然而，岩土工程勘察中所获得的资料往往十分有限。基于有限数据采用不同方法计算的土性参数波动范围会存在显著差异，难以做出比较[15]。其次，天然土体中土性参数真实的波动范围往往是未知的[16,17]，依据工程场地勘察资料采用各种波动范围求解方法的可靠性尚待考究。因此，有必要研究有限数据条件下各种波动范围求解方法的有效性，为合理选择土性参数波动范围计算方法提供参考依据，从而为应用随机场模型准确描述土性参数空间变异性提供所必需的输入信息。

本文模拟生成静力触探试验数据，通过对有限模拟数据的分析对比了求解波动范围的平均零跨法、相关函数法、拟合理论方差折减函数法、拟合简化方差折减函数法及贝叶斯方法的有效性。首先假定静力触探试验锥尖阻力真实的波动范围，生成锥尖阻力模拟数据。然后，基于有限模拟数据分别采用不同方法计算其波动范围，并与其真实值对比，以此说明各种计算方法的准确性，探讨各种方法的适用性。

1 波动范围计算方法

波动范围是描述土性参数空间变异性的重要指标，计算方法主要有平均零跨法、递推空间法、回归模拟法、相关函数法、拟合方差折减函数法及贝叶斯方法等。本文主要对比分析平均零跨法、相关函数法、拟合理论方差折减函数法、拟合简化方差折减函数法及贝叶斯方法的有效性，下面分别介绍这些方法。

(1)平均零跨法

(1)

(2)相关函数法

相关函数法是通过不同类型理论的相关函数ρ(τ)拟合样本的相关函数，选择拟合度最优的相关函数积分求解波动范围[19～21]。应用相关函数法时，其计算结果受所选相关函数类型的影响很大。由于样本数量的限制，根据测量数据求得的相关系数ρ(τ)在后半段会出现剧烈振荡(见图1)，给选取最优相关函数类型带来了困难。即便采用最优的相关函数，由于ρ(τ)值在后半段剧烈振荡，估计的波动范围偏差也比较大。为了提高相关函数法估计波动范围的可靠性，Uzielli等[22]提出利用ρ(τ)超过Bartlett值的初始部分数据拟合相关函数，从而估计波动范围。

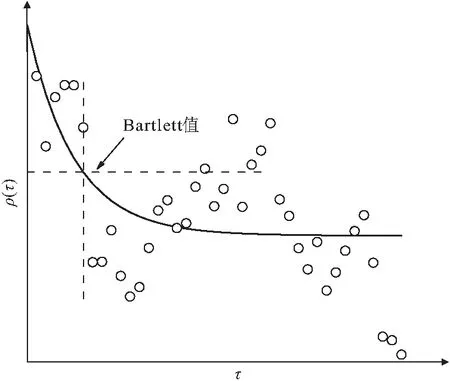
图1 相关函数法

(3)拟合理论或简化方差折减函数法

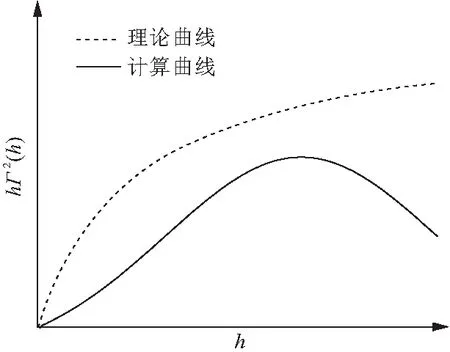
图2 hΓ2(h)-h曲线

拟合方差折减函数法是把曲线hΓ2(h)-h上最大值(hΓ2(h))max对于h作为平稳点，即为hmax。然后根据数值(h,hΓ2(h)) (0≤h≤hmax)用理论的方差折减函数或简化的方差折减函数进行曲线拟合[1](如图3所示)。

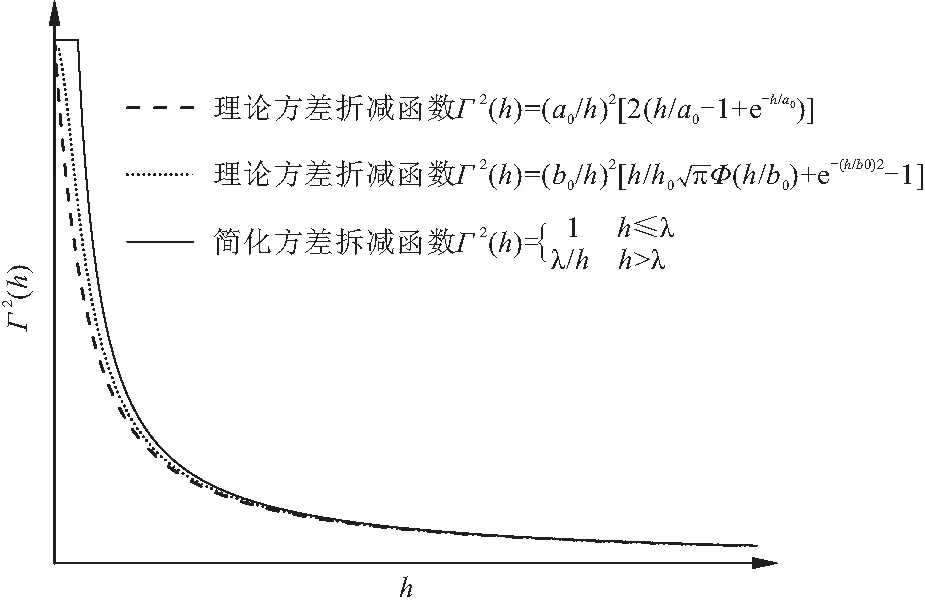
图3 拟合方差折减函数法

(4)贝叶斯方法

贝叶斯方法充分融合多源信息(包括有限勘探数据和先验信息)，将未知参数看作随机变量，认为在获得测量数据前就已存在一个概率分布，称之为先验分布，在测量数据下未知参数的条件分布称为后验分布，后验分布是对未知参数进行统计推断的依据[23]。令X为所关心的未知参数，基于贝叶斯理论，未知参数X的后验分布可以表示成[23]

P(X|Data)=K-1P(Data|X)P(X)

(2)

式中：P(Data|X)为给定参数X情况下测量数据的概率密度函数，称为似然函数；X为未知参数；Data为测量数据；P(X)为参数X的先验分布，反映了获取测量数据前对X的认识；K=P(Data)，是与X无关的常数；P(X|Data)为参数X的后验分布，反映了在先验信息和测量数据下参数X的更新信息。

2 静力触探试验数据模拟

静力触探试验(Cone Penetration Test,CPT)是原位试验中最常用的一种测试技术，它可以采集连续的样本数据，取样间距较小。最小取样间距为0.02 m，测量精度非常高，测量误差可以忽略不计。并且静力触探还可以以不同取样间距采集数据来适应不同成因土性参数波动范围的要求，广泛地用于研究土性参数的波动范围[11～14]。本文以静力触探试验的锥尖阻力为研究对象，模拟锥尖阻力的测量数据。通过模拟数据分析，比较各种波动范围计算方法的有效性。

ρ(τ)=exp(-2|τ|/λ)

(3)

式中：ρ(τ)为垂直方向上两点的相关系数；τ为垂直方向上两点的相对距离。

ξ=lnqN的空间变异性可以定量表征为：

(4)

文献资料[22]中，CPT锥尖阻力qN的均值与标准差分别取为固定值μ=300，σ=120。取CPT模拟数据的样本间距ΔD=0.02 m，lnqN波动范围λ分别取 0.1，0.4，0.8，1.2 m，样本长度分别取I=D/λ=5，10，20，30，40，50。对不同波动范围(如λ=0.1，0.4，0.8，1.2 m)，根据式(4)分别在不同样本长度I条件下重复模拟20套lnqN数据。例如已知qN的均值与标准差，lnqN相关函数为指数型，CPT样本间距为0.02 m。当lnqN波动范围λ取 0.1 m时，CPT样本长度I为5时，由方程(4)可以模拟一套lnqN数据(如图4)，重复生成20套lnqN随机模拟数据。

图4 CPT锥尖阻力模拟数据(λ=0.1 m，样本长度I=5)

分别采用平均零跨法、相关函数法、拟合理论方差折减函数法、拟合简化方差折减函数法以及贝叶斯方法计算锥尖阻力波动范围值。采用贝叶斯方法时，锥尖阻力波动范围的先验分布根据其经验取值范围取为均匀分布。由文献[22]和[24]可知，波动范围经验取值范围为[0.1 m, 1.2 m]。基于先验信息和模拟的CPT 数据，即可得到波动范围的后验分布，即方程(2)，具体可参考文献[10]。本文采用马尔科夫链蒙特卡洛模拟(Markov Chain Monte Carlo Simulation，MCMCS)的Metropolis-Hastings 算法[10]求解后验分布，生成50000个波动范围的MCMCS 样本，然后基于波动范围的MCMCS随机样本估计其后验均值。

3 波动范围计算方法有效性分析

3.1 波动范围估计值比较

分别采用不同方法计算锥尖阻力波动范围值，并统计20套重复模拟数据计算的波动范围平均值λm及变异系数Covλm。图5给出了五种方法计算结果。

图5 不同波动范围计算方法估计结果

由图5还可以看出，不同波动范围计算方法的适用性受CPT样本数据量的影响。如图5a，当锥尖阻力真实波动范围取λ=0.1 m，CPT样本长度I=5，10时，相关函数法无法估计波动范围值。当真实波动范围λ=0.1 m，CPT样本长度I=5时，拟合理论方差折减函数法和拟合简化方差折减函数法无法计算波动范围。原因在于当样本长度非常小时，相关函数法中相关系数超过Bartlett值的数据十分有限，当数据量恰好等于1时则无法计算两点间相关系数，从而导致无法估计波动范围。拟合理论方差折减函数法和拟合简化方差折减函数法因难以计算实际的方差折减函数，所以无法计算波动范围值。然而，当真实波动范围取λ=0.1 m，CPT样本长度I为5，10时，贝叶斯方法和平均零跨法可以估计波动范围值。由此可见，当锥尖阻力真实波动范围值较小，且静力触探试验样本数据量较少时，相关函数法、拟合理论方差折减函数法以及拟合简化方差折减函数法无法计算锥尖阻力波动范围，而贝叶斯方法和平均零跨法可用于估计岩土参数波动范围值。但需要注意的是，平均零跨法适用于岩土参数相关结构为高斯型，对于本文锥尖阻力真实相关函数为指数型，平均零跨法计算结果偏差较大。

此外，由图5还可以看到，随着CPT样本长度增加，贝叶斯方法、相关函数法与拟合理论方差折减函数法估计的λm/λ逐渐趋近于1，即λm逐渐逼近真实值λ，而且偏差越来越小。拟合简化方差折减函数法与平均零跨法虽然也有逼近真实值的趋势，但总体上估计结果仍偏小，如图5a所示，当样本长度I=50时，此时样本容量n=Iλ/ΔD=250，拟合简化方差折减函数法与平均零跨法计算的λm/λ仍然偏离1，而其他三种方法则接近于1。由图5还可知，当静力触探试验样本长度I≥20时，贝叶斯方法、相关函数法与拟合理论方差折减函数法估计的波动范围值非常接近。说明当静力触探试验样本数据充分时，均可采用三种方法计算波动范围值。

3.2 波动范围估计结果的不确定性分析

为了进一步说明不同波动范围计算方法的可靠性，图6对比分析了贝叶斯方法、相关函数法以及拟合理论方差折减函数法计算波动范围值的不确定性。因平均零跨法与拟合简化方差折减函数法估计波动范围值存在显着偏差，此节仅对比其他三种方法估计结果的不确定性。

图6 不同方法估计波动范围值的不确定性对比

由图6可知，在相同CPT数据量条件下贝叶斯方法计算的波动范围的变异系数Covλm最小，相关函数法与拟合理论方差折减函数法计算的变异系数Covλm较为接近。说明贝叶斯方法求解波动范围值的不确定性较小，计算结果较为准确可靠，相关函数法与拟合理论方差折减函数法计算结果的不确定性较为接近。这是因为相关函数法和拟合理论方差折减函数法则是基于部分测量数据拟合理论相关函数或理论方差折减函数计算波动范围，所以两种方法的计算结果相近。而贝叶斯方法则充分融合了多源信息(包括有限观测数据和先验信息)，所以计算结果的不确定性较小。综合波动范围估计值以及计算结果不确定性的对比可知，在这些方法中贝叶斯方法计算准确性最高、适用性最强，它既适用于数据量较多的情况，也适用于数据量较少的情况。

4 结 论

本文基于模拟的静力触探试验数据对比了计算土性参数波动范围的平均零跨法、相关函数法、拟合理论方差折减函数法、拟合简化方差折减函数法以及贝叶斯方法的有效性。通过不同求解方法计算波动范围值与变异系数的对比，主要得出以下结论：

(1)通过真实相关函数为指数型相关函数的静力触探试验模拟数据分析，不同计算方法确定波动范围的准确性存在一定差异。贝叶斯方法确定的波动范围最接近于真实值，其次是相关函数法与拟合理论方差折减函数法，平均零跨法因其是在假定相关函数为高斯型的前提下提出来的，计算结果存在较大误差，使用时应当注意其假定条件，拟合简化方差折减函数法因近似的方差折减函数不一定与实际方差折减函数相同，计算结果存在一定偏差。

(2)CPT样本数据量影响波动范围计算方法的适用性。当锥尖阻力真实波动范围较小，且静力触探试验样本数据量非常有限时，贝叶斯方法和平均零跨法可以估计波动范围值，但相关函数法、拟合理论方差折减函数法和拟合简化方差折减函数法无法计算波动范围。如本文锥尖阻力真实波动范围取λ=0.1 m，CPT样本长度I=5，10时，相关函数法无法估计波动范围。锥尖阻力真实波动范围λ=0.1 m，且CPT样本长度I=5时，拟合理论方差折减函数法和拟合简化方差折减函数法不适用于确定波动范围。

(3)当静力触探试验数据量较多时，如本文CPT样本长度I≥20时，贝叶斯方法、相关函数法与拟合理论方差折减函数法估计的波动范围非常接近，此时均可采用这三种方法计算波动范围值。

(4)在静力触探试验数据量相同的条件下，相关函数法与拟合理论方差折减函数法计算的不确定性接近，贝叶斯方法因其充分融合了多源信息(包括有限观测数据和先验信息)，计算波动范围值的不确定性最小。综合波动范围估计值以及计算结果不确定性的对比可知，贝叶斯方法准确性最高、适用性最强，既适用于数据量较多的情况，也适用于数据量较少的情况。