基于RF-NSGA-II的建筑能耗多目标优化

吴贤国， 杨 赛， 王成龙， 王洪涛， 陈虹宇， 朱海军， 王 雷

(1. 华中科技大学 土木与水利工程学院， 湖北 武汉 430074； 2. 中建三局集团有限公司， 湖北 武汉 430064；3. 南洋理工大学 土木工程与环境学院， 新加坡 639798 )

能源消耗一直是世界各国备受关注的问题，其中建筑能耗问题同样需要引起重视。在建筑的使用阶段，建筑外围护结构对建筑能耗影响占50%，为了降低室内外环境的能量传递，合理选择外围护结构是十分关键的问题，因此，近年来，开展了通过提高建筑外围护结构性能使建筑能耗降低的研究。

无论是国内或国外，在对建筑能耗进行研究时，侧重于建筑能耗预测[1,2]和建筑能耗优化[3～5]。在建筑能耗预测研究中，任宏等[6]以STIRPAT(Stochastic Impacts by Regression on Population，Affluence,and Technology)模型构建城镇建筑能耗影响因素模型，利用最小二乘法和岭回归分析对模型进行计算分析。莫甘茗[7]摸索出基于多元线性回归的以建筑类型、面积为参数的建筑能耗预测与建筑节能分析模型。房涛等[8]首先通过单因素敏感性分析筛选出关键设计参数，然后通过正交试验设计进行仿真计算，并进行多重线性回归。Yang等[9]通过具有非线性自回归外生结构的动态人工神经网络，利用在线建筑运行数据定期更新建筑模型。Seyedzadeh等[10]提出了一种优化最大似然模型的方法，用于预测热负荷和冷负荷，并可以搜索可能的参数空间。在能耗优化研究中，庞宇馨等[11]利用能耗模拟软件DeST-c模拟研究该建筑在三种不同气候分区下围护结构热工性能与建筑能耗的关系，并利用全寿命期费用评价方法进行评价。牧仁[12]利用能耗模拟软件DeST-h计算围护结构参数对冬季采暖能耗的影响，通过正交实验得出优化方案。何立华等[13]将供暖和照明能量负荷之和作为目标函数，建立函数关系，以能耗最小化为目标，采用遗传算法进行优化求解。Ferrara等[14]利用仿真模拟技术对建筑进行建筑能耗模拟，提出了近零能耗建筑方案设计原则并利用单目标优化方式对建筑能耗参数进行优化；Brinks等[15]以制定开发成本最优的解决方案为这项工作的重点，以满足NZEB标准。其结果比德国现行(2015年)建筑标准的热能需求低50%～75%。

以上研究均对建筑能耗研究有所贡献，但建筑能耗预测无法充分将预测成果运用到实践中，导致实际意义不大；同时以上建筑能耗优化没有考虑多个目标，与实际情况不太符合，因此本文将利用RF-NSGA-II模型，先通过DesignBuilder和正交试验获取建筑能耗数据，再利用RF(Random Forest)对建筑能耗模拟数据进行预测，最后将建筑能耗预测回归函数作为适应度函数之一，引入热舒适度函数为另一个适应度函数，最后利用NSGA-II(Non Dominated Sorting Genetic Algorithm-II)算法对建筑能耗和热舒适度进行优化，从而获得符合实际意义的建筑能耗和热舒适度最优解。

1 理论基础

1.1 随机森林基本原理

随机森林(Random Forest,RF)作为一种机器学习算法，在2001年由Breiman提出。该算法可以用于解决处理分类和回归问题，由于其强大的数据挖掘能力和高预测精度，广泛用于预测和特征选择等问题。

随机森林回归模型是在数据样本X和预测变量Y的基础上，生成依赖于随机变量θ决策树形成的，设单棵决策树预测器h(X,θk)的预测结果为hi(X)，则随机森林回归模型的最终预测结果表示为：

(1)

该算法通过对样本数为ntree的原始数据进行随机抽样，得到ntree个训练子集，然后将ntree个训练子集生成相同分布的ntree棵决策树，进而构成一个随机森林模型h(X,θk),k=1,2,…,ntree，X表示输入向量，θk是表示生成每棵树生长路径的向量。当RF树生长时，假如样本数据的特征数有M个，先设定一个小于M的正整数mtry(一般取M/3)，在生成决策树的过程中，需要对树节点进行分割，随机从M个特征中抽取mtry个作为候选特征，随机子集中的每个节点用mtry个特征进行最佳分割，可以降低CART树之间的相关性，进而降低随机森林模型泛化误差，且随着决策树数量的增加，森林的泛化误差接近极限。随机森林模型的预测平均泛化误差可表示为：EX,Y(Y-h(X))2，当决策树棵数ntree接近无穷大时，模型平均泛化误差表示为：

EX,Y(Y-avkh(X,θk))2→EX,Y(Y-Eθh(X,θ))2

(2)

式中：avk表示取其平均值；Eθ表示求期望。

故单棵回归树的平均泛化误差PE*(tree)表示为：

PE*(tree)=EθEX,Y{[Y-h(X,θ)]·[Y-h(X,θ*)]}

(3)

对于所有的θ，都能得到E(Y)=EXh(X,θ)，则有：

(4)

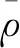
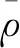
1.2 NSGA-II算法基本原理

Deb等[16]于2002年为改善遗传算法多目标优化性能及精度，对NSGA进行改进，得到带精英策略的非支配排序遗传算法(NSGA-II)。NSGA-II的最大优势就是大幅度降低计算复杂程度同时拓宽采样空间[17]。

NSGA-II算法最核心的特点是快速非支配排序、拥挤距离及精英策略。其中NSGA的非支配排序为O(MN3)，改进后非支配排序O(MN2)(M为目标数，N为种群大小)，通过非支配排序的改善提升了种群排序的速度。拥挤距离法采用了拥挤度和拥挤度比较算子计算每个解的距离。第i个解的拥挤距离计算如下：

(5)

NSGA-II算法引入了精英策略，可以扩大采样空间，提高了算法的运算速度和鲁棒性的同时，避免最佳个体的丢失。

1.3 基于RF-NSGAII算法的多目标优化模型

在各种研究领域中，所涉及的各种变量之间会存在高度非线性的复杂关系，为了获取各种变量之间的具体函数关系，可以利用随机森林模型替代传统的数学函数。同时随机森林模型作为遗传算法适应度函数，可以实现精度更高，效果更好的优化。RF-NSGAII算法的具体流程如图1所示。

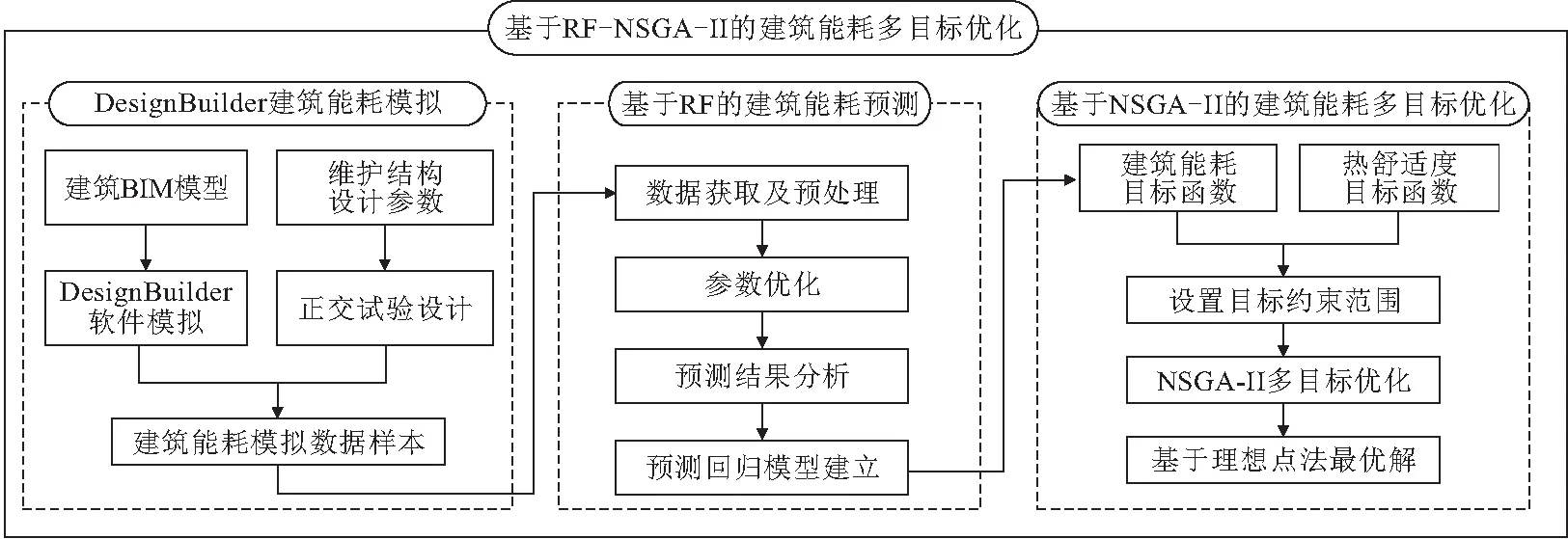
图1 基于RF-NSGA-II的建筑能耗多目标优化流程

1.3.1 DesignBuilder建筑能耗模拟

(1)基于BIM和DesignBuilder的建筑能耗计算

BIM(Building Information Modeling)技术具有可视化、协调性、模拟性、优化性四大优势，因此将BIM技术做为核心技术应用到各种建筑项目软件中，可以为建筑施工运营分析提供自动化、智能化基础和平台[18]。因此，本文利用Revit软件建立BIM模型，然后将模型导入DesignBuilder软件生成建筑能耗仿真模型，在DesignBuilder软件中对模型的相应参数进行设置，实现对建筑模型的能耗进行计算。

(2)正交试验获取数据集

正交试验设计方法既满足试验科学性，又可以顾及试验的工作量以及复杂程度，因此本文采用正交试验获取建筑能耗数据集。首先依据建筑设计规范对每个围护结构设计因子水平进行合理划分，然后通过Allpairs软件获取正交设计水平表，最后，将建筑物BIM模型导入DesignBuilder中，并分别输入经正交试验得到的试验方案进行各外围护结构参数处在不同水平下的建筑能耗模拟，输出DesignBuilder中获取的建筑能耗结果。

1.3.2 基于RF的建筑能耗预测

Step1：数据获取及预处理

本文研究的是建筑外围护结构部分设计参数给建筑能耗带来的影响，以建筑能耗仿真结果为数据预测样本集，选择与建筑能耗紧密相关的影响因素作为样本特征值并作为预测模型的输入指标。数据预处理主要是对建筑能耗数据进行归一化，如果在预测过程中不进行归一化处理，样本中一些数据过大或过小，都会增加训练过程中算法的负担，会导致数据被淹没或网络不收敛。

Step2：随机森林的参数设置及建模

(1)样本分集

以原始数据集中大约2/3的数据作为RF模型的训练样本集，余下包含了原始数据集中1/3的数据作为RF模型的测试样本集。

(2)参数选择

建模过程中，主要涉及两个参数：回归树的棵数ntree和随机特征的数目mtry。ntree的值会影响随机森林模型的训练度和精确度，一般ntree的值越大，模型的精度越高；mtry控制了随机森林模型属性的扰动程度，mtry一般根据经验公式确定，设数据集中的变量个数为P，默认情况下mtry=P(分类模型)或mtry=P/3(回归模型)。

确定了两个参数后，即可利用RF算法对训练样本集和测试样本集建立起随机森林回归模型。

Step3：预测结果分析

为了验证RF模型的预测精度，通过两个模型性能的指标均方根误差RMSE和拟合优度R2来进行检验。均方根误差RMSE体现预测值与真实值的离散程度，拟合优度R2用于验证预测值与真实值之间的拟合程度，两个指标分别由式(6)(7)得出：

(6)

(7)

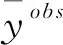
1.3.3 NSGA-II多目标优化

Step1：建立目标函数

(1)基于RF的建筑能耗目标函数

引入RF建筑能耗回归预测算法替代传统数学函数作为多目标遗传算法中的目标函数，可以很好地解决输入变量与输出目标之间存在复杂非线性关系，无法给出具体函数表达式的问题。建筑能耗回归函数f1如式(8)所示：

f1=RFregression(x1,x2,…,x7)

(8)

式中：x1～x7分别为外墙综合传热系数、外墙太阳辐射吸收系数、屋面综合传热系数、屋面太阳辐射吸收系数、外窗综合传热系数、外墙得热系数以及窗墙比。则建筑能耗目标函数用minf1表示。

(2)室内热舒适度目标函数

室内热舒适度是一个可以用来描述在客观室内环境中，大多数人在心理和生理方面达到满意状态程度的重要指标，可用预测平均投票数PMV进行评价，正值表示热，而负值表示冷，且值越接近于0表示热舒适度越高。根据ISO 7730标准，建立基于人体热平衡方程和主观热感觉的热舒适度评价指标PMV公式[9]：

PMV=0.303×10-0.036M+0.0275×{M-W-0.014M(34-ta)-3.054[5.733-0.007(M-W)-Pa]-0.42(M-W-58.15)-0.0173M(5.867-Pa)-3.9610-8fcl(tcl4-ts4)-fcl·hcl(tcl-ta)}

(9)

式中：M表示人体新陈代谢率；W为人体做工的机械功率；ta为室内空气温度；tcl为着装人体表面平均温度；fcl为服装的面积系数；hcl为对流换热系数；Pa为人体周围水蒸气分压力;ts为围护结构辐射温度。

(10)

式中：Fn j为围护结构各表面面积；tn j为各围护结构表面温度。考虑外围护结构设计参数，可得PMV与外围护结构之间的关系式为：

PMV=0.303e-0.036M+0.0275{M-W-0.014M(34-ta)-3.054[5.733-0.007(M-W)-Pa]-0.42(M-W-58.15)-0.0173M(5.867-Pa)-3.9610-8fcl{tcl4-[(F外窗t外窗+F外墙t外墙+F屋面t屋面)/(F总+F屋面)]4}-fcl·hcl(tcl-ta)}

(11)

式中：F总为建筑外围总表面积；F外墙，F外窗，F屋面分别为外墙、外窗和屋面的外表面积；t外墙，t外窗，t屋面分别为外墙、外窗和屋面的表面温度。则基于外围护结构设计参数的热舒适度目标函数minf2如式(12)：

minf2=min|PMV(x1,x3,x5,x7)|

(12)

Step2：建立目标约束范围

为了使得生成的方案更加合理可行，需要对方案生成时的各个因素设定限制范围，形成变量的约束条件，约束条件的一般形式如下：

bil≤xi≤biu

(13)

式中：xi为第i个设计参数；bil和biu分别为第i个设计参数值的下限和上限。

Step3：NSGA-Ⅱ多目标优化

当目标函数和约束条件都确定下来之后，便可基于NSGA-II算法实现多个目标优化，可以找到基于外围护结构设计参数的Pareto最优解集。与传统遗传算法GA相比，NSGA-II算法的关键步骤主要有两个：

(1)在设置初始种群后，NSGA-II算法将通过快速非支配排序后，利用三个遗传机制获得首批子代种群。

(2)第二代种群将父、子代合并，再一次通过快速非支配排序，计算个体之间拥挤距离之后，按步骤一再次产生新的子代种群。

Step4：基于理想点法获取最优解

利用NSGA-II算法获取的Pareto最优解集并不是唯一的解，为了获取唯一最优解，可以采用理想点法。理想点是指利用各个目标的最优值组成的点E(ηEpoint，ZEpoint)。

找出对应的理想点后，计算Pareto最优解图中各个最优解到理想点之间的距离Un，计算公式如下：

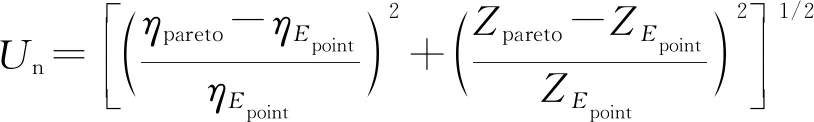
(14)

式中：(ηpareto，Zpareto)为最优Pareto前沿点对应的坐标；(ηEpoint，ZEpoint)为理想点对应的坐标。通过计算距离函数，最优点是距理想点最小距离的点：

Uopt=minUn

(15)

因此，利用理想点法可从Pareto前沿解集中确定使得多目标函数达到最优的一组最优解。

2 基于RF-NSGA-II算法的建筑能耗多目标优化

2.1 工程背景

以铁科高速公路松原至通榆(吉蒙界)段高速公路建设项目房建工程为例。本项目起自松原市与大广高速交叉处拐脖店互通，经前郭县、乾安县后进入白城市境内，再经通榆县，止于吉林省白城市通榆县与内蒙古自治区科右中旗交界处(吉、蒙省界)。本项目的建设，对于贯彻落实国家振兴东北老工业基地、“一带—路”和东北亚开发开放等战略，完善国家高速公路网与互联互通大通道，改善沿线交通条件，促进区域优势资源开发和经济社会协调发展等均具有重要意义。图2为该工程BIM模型效果图。

图2 BIM模型

2.2 DesignBuilder建筑能耗模拟

由于外围护结构设计参数对建筑能耗会造成较大的影响，因此，本文将外墙综合传热系数、外墙太阳辐射吸收系数、屋面综合传热系数、屋面太阳辐射吸收系数、外窗综合传热系数、外窗得热系数、窗墙比等7个围护结构参数作为建筑能耗模拟参数变量，根据每个参数的建议取值范围对因子水平进行合理划分，利用Allpairs软件设计正交表，如表1所示；并利用DesignBuilder模拟32组不同因子水平下的参数组合，依次输入DesignBuilder中进行建筑能耗仿真，图3为基于BIM-DesignBuilder建筑能耗模拟建模，正交试验建筑能耗结果如表2所示。

2.3 基于RF的建筑能耗预测2.3.1 数据获取与预处理

将表2中的32组能耗模拟样本数据作为建立随机森林预测模型的原始样本，随机选取24组数据作为随机森林模型的训练集，用于学习建筑能耗和围护结构参数的非线性映射关系，实现能耗预测，剩下的8组数据作为测试集以检验预测效果。并对所有样本数据进行归一化处理，将建筑能耗数据范围控制在[-1,1]之间，避免因数据维度不同造成对预测结果的误差。

表2 能耗模拟结果

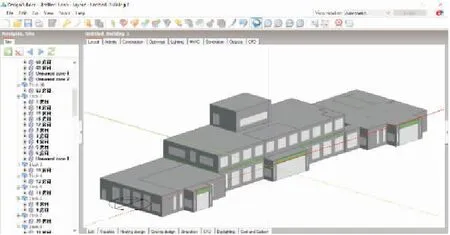
图3 基于BIM-DesignBuilder的建筑能耗模拟

2.3.2 参数优化

由于选取的训练样本特征数较少，决策树参数最大特征数max_features可以设置为auto，最大叶子节点数max_leaf_nodes、决策树最大深度max_depth均为默认；节点划分最小不纯度min_impurity_split默认为1×10-7。

基于python代码进行随机森林回归模型调参，因此重要参数仅需考虑n_estimators，训练性能评价指标为R2。图4为训练集真实值与预测值间的R2随n_estimators变化曲线。从图中可以看出，n_estimators为195时，R2最大值为0.9998，表明模型具有较高的预测精度和较强的泛化能力。

图4 参数选择结果

2.3.3 建筑能耗预测结果

利用上述优化后的参数，利用训练集建立学习模型，分别输出训练集和测试集的能耗预测结果，如图5，6所示。

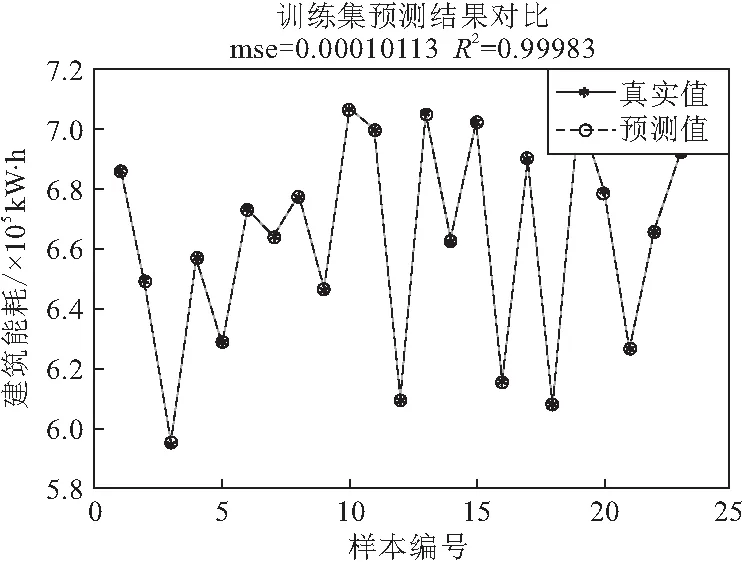
图5 训练集预测结果

图6 测试集预测结果对比

从图5可以看出，训练集对建筑能耗进行预测得到的结果与仿真模拟情况基本上一致，拟合度R2为0.9998，均方根误差为0.0001，验证了随机森林预测模型精准的预测效果。从图6可以看出，测试集对建筑能耗进行预测结果与仿真模拟基本上一致，拟合度R2为0.9858，均方根误差为0.0066，充分验证了训练集预测拟合函数的正确性。

2.4 基于RF-NSGA-II建筑能耗多目标优化2.4.1 建立目标函数

(1)RF建筑能耗目标函数

利用RF训练后建筑能耗与外围护结构参数的预测拟合关系，以能耗最低为目标利用式(8)建立建筑能耗目标函数minf1为：

f1=min(RFregression(x1,x2,x3,x4,x5,x6,x7))

(2)室内热舒适度目标函数

为了获得教学楼建筑室内的热舒适度取值，将根据项目实际情况对相关参数进行设置，并根据上述参数的取值，代入式(12)，由于PMV值趋于0时，舒适越高，故可得基于外围护结构设计参数利用式(12)的目标函数minf2：

minf2=min|PMV(x1,x3,x5,x7)|

2.4.2 建立多目标约束范围

多目标优化模型的约束条件基于GB 50176-2016《民用建筑热工规范》被动式超低能耗绿色建筑技术导则》和GB 50189-2015《公共建筑节能设计标准》确定建筑外围护结构设计参数的取值范围，具体表示为：

2.4.3 基于NSGA-Ⅱ的多目标优化

针对采用的NSGA-II算法，将种群类型为双向量即两个目标种群规模设置为40，最大进化代数设为100，基于python的geatpy工具箱，根据建筑能耗和热舒适度两个目标函数，搜寻全局最优解，获得最优Pareto前沿图，如图7所示，图中包含40对最优解，表3给出了图7中部分最优值点以及对应的决策变量组合。

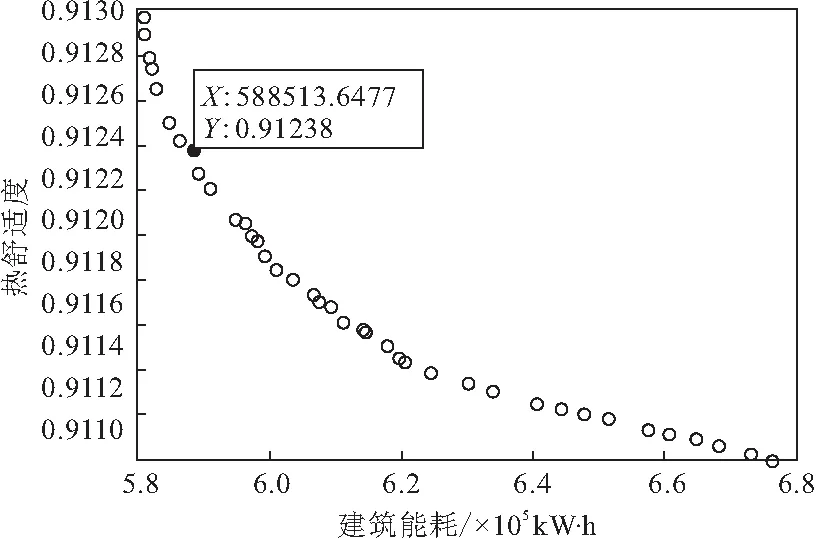
图7 最优Pareto前沿

2.4.4 基于理想点法的最优解

由2.4.3可知，基于NSGA-II算法所得到的最优解不存在唯一性，因此，为了获得一组最优解，可以采用理想点法。建筑能耗与PMV所对应的最优值构成的理想点坐标为E(580875，0.912967)，如图8所示，得到理想点后，根据式(14)(15)可得建筑能耗多目标优化最优解(588513.6477，0.91238)，表4为目标最优和实际值及其对应最优解。

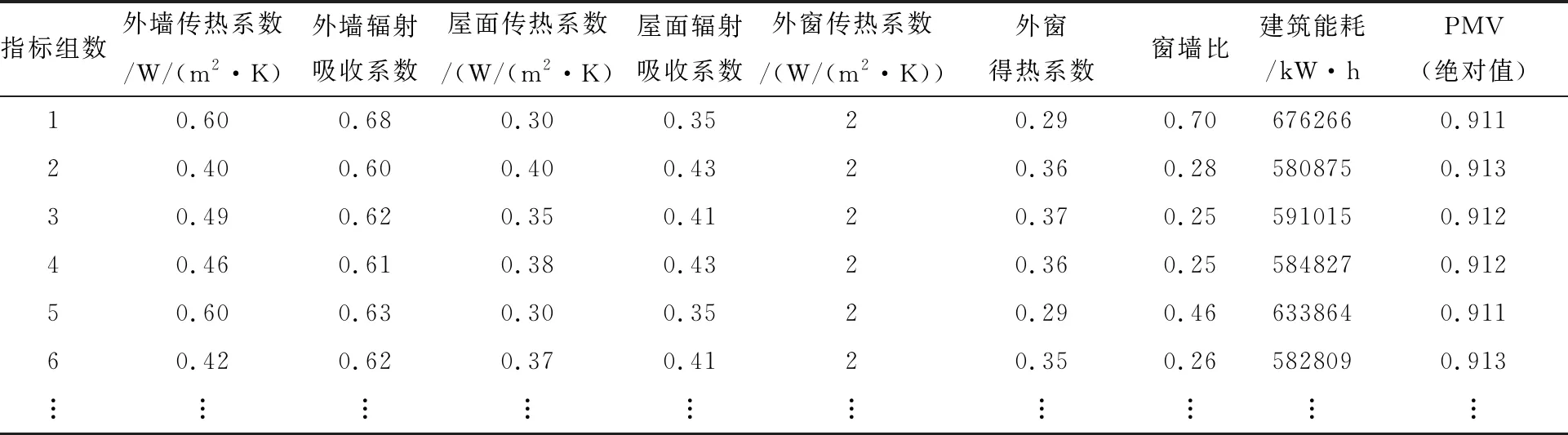
表3 目标最优值及对应解

表4 目标最优和实际值及其对应最优解

图8 多目标优化最优解

利用NSGA-II算法进行多目标优化后，建筑能耗和建筑室内热舒适度均得到改善，项目建筑在原有围护结构初始值下所产生的建筑能耗总量为692710 kW·h，在对建筑外围护结构设计参数进行优化后，建筑能耗总量为588514 kW·h，比原设计的建筑能耗降低了15%，体现了建筑能耗优化具有较好的效果；原热舒适度PMV的绝对值为1.21，优化后室内热舒适度PMV的绝对值为0.91，比原设计的室内热舒适度PMV的绝对值下降了24.8%，充分验证了在进行多目标优化后，室内热舒适度有明显的改善。

3 结 论

(1)本文建立了一种基于RF-NSGA-II多目标优化模型，首先基于BIM利用DesignBuilder进行正交试验能耗模拟，利用RF对建筑能耗实现高精度预测，将建筑能耗预测回归函数作为适应度函数，以热舒适度为另一个适应度函数，结合规范及工程项目的要求建立维护结果参数相关的约束条件，利用NSGA-II算法进行多目标优化，得到最优值。

(2)利用随机森林对基于建筑外围护结构设计参数的建筑能耗进行预测有良好效果。在对建筑能耗预测进行实例分析中，预测模型的拟合度高达0.9858，均方差为0.0066，充分体现了随机森林预测模型的良好预测拟合效果，也证实了以随机森林回归函数作为建筑能耗目标函数的合理性。

(3)从NSGA-II算法多目标优化结果来看，建筑能耗和室内热舒适度两个目标均较原有设计有所改善，其中，建筑能耗从原有692710 kW·h降至588514 kW·h，比原有的建筑能耗降低了104196 kW·h，节能效果显著；原有室内热舒适度PMV的绝对值为1.21，优化后室内热舒适度PMV的绝对值为0.91，PMV值降低了0.3左右，热舒适度也得到了改善。该模型对工程实践具有一定的指导作用。