气幕防波堤设计

翟建国，刘庆茶，黄筱云，胡勇虎，伍炳坤

（1.中交武汉港湾工程设计研究院有限公司，湖北 武汉 430040；2.长沙理工大学 水利工程学院，湖南 长沙 410114）

引言

防波堤用于保护港口和沿海地区免受海浪袭击。现有的防波堤建造费用高昂，且成本随着水深和海浪气候的恶劣程度而增加。气幕防波堤被认为是传统防波堤潜在的替代品。它由海底开孔管释放出来的气泡组成，与传统的防波堤相比，气幕防波堤安装容易，建造成本非常低，且不会干扰船舶航行。气幕防波堤的消波效果与单位时间内气泡释放量相关，因此，对空气压缩机的要求很高。因此，气幕防波堤一般可作为临时保护措施，或与其它防波堤结构形式相结合。

采用水下气幕阻止或削弱波浪传递的方法是由美国人菲利普·布拉瑟在1907年提出的，并在1915年应用于保护标准石油公司在加州埃尔塞贡多市的码头[1]。1936年，Thysse指出气泡羽流引起表层水平流动是气幕消波的主要机制[2]。1939～1945年，二次世界大战期间，英国White和Taylor教授认为气幕具备良好军事用途，开展了相关基础研究，首次预测了消减波浪所需表层流速大小以及产生该流速所需的气量[2]。1955年，Evans在英国运输委员会码头和水路水力学实验室62英尺长的波浪水槽开展一系列试验，证实气幕消波机理是气泡羽流引起表层水平流动从而消减波浪高度，并且消波效果与波长、波高、水深以及表层水流厚度有关[3]。同年，Taylor采用势流理论推导了任一波浪完全衰减所需的水平流动大小与厚度，并运用施密特线源热羽流理论给出气幕中心垂向速度和表面水平速度的大小及厚度[4]。1960年，Bulson在英国南安普顿特拉法加干船坞内开展深水条件下气幕帘试验研究[5]；1962年，他在费特姆船舶流体力学实验室3号水槽开展了大尺度气幕防波堤试验[6]；1968年，他根据所获得试验结果提出了气幕防波堤设计理论[7]。1965年，Kurihara通过大尺度试验指出气泡的可压缩性和气泡相对上升速度会对气幕防波堤性能造成影响[8]。在德国，Hensen（1955年，1957年）在实验室和现场分别开展试验，指出采用Froude数相似计算不同尺度试验供气量不合适[9-10]。1960年，Preissler基于其试验结果提出了消减波浪波高至一定值所需的供气量计算公式[11]。1978年，Iwagaki将气幕帘与潜堤、浮式防波堤结合，提出了复式气幕防波堤结构，试验结果表明，复式结构较单一结构消波性能更好[12]。在我国，王永学等（2005）提出了确定比尺试验中所需供气量的相似律[13]；张成兴等（2010）通过试验和数值模拟分析双排气幕帘的消波效果，结果显示，相同供气量下双排气幕消波效果不及单排气幕[2]；王延续等（2019）通过数值模拟分析了潜堤与气幕帘组合的消波效果，并指出，若优化该复式防波堤结构能有效阻挡长周期波的传递[14]；许条建等（2019）通过数值模拟分析气幕防波堤的水动力特征[15]。

本文将介绍气幕防波堤消波机理，并给出气幕防波堤供气量的计算方法，为气幕防波堤的设计提供参考。

1 气幕防波堤消波机理

假定由气幕羽流产生的水平流速U从水面向下线性减小，如图1所示。

图1 气幕帘产生的水平流速垂向分布

其中，表面水流的速度势为：

表面水流以下流动速度势为：

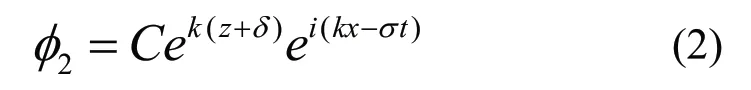
表面水流上边界波动方程为：

下边界波动方程为：

式（1）～（4）中：u为表面水流速度；k为波速；σ为圆频率；δ为表层水平流动厚度；η为表面高度。

根据表层水流上下边界运动边界条件，有

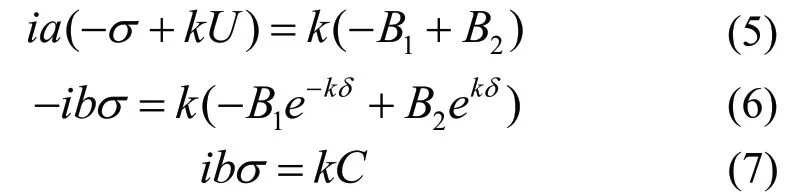
根据上下边界动力边界条件：

消去边界条件中的待定系数，得：

其中，

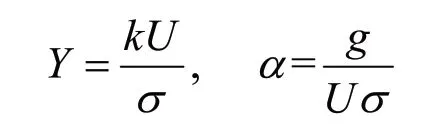
前者表示水流速度与波速比值，后者是水流弗劳德数的倒数。

定义：

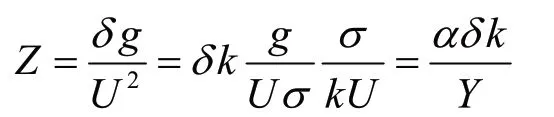
可以看出，参数Z只与气幕帘本身有关。当Z为常数时，-α存在最小值-αm，负号表示U与波浪传播方向相反。当波浪圆频率σ≥-g/Uαm时，波浪将无法抵御水流作用继续传播。

当表层水流厚度远小于波长，即kδ＜1。将上式以kh的幂级数展开，忽略kh二次及以上的高次项，则：

其中：

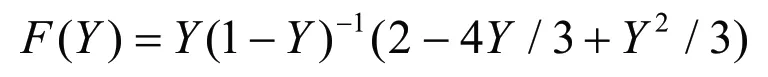
深水条件下，表层水流能够抵御的最大波长为：

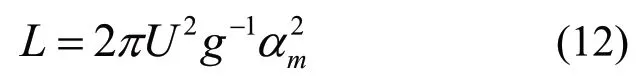
有：

2 气幕防波堤设计原理

根据Taylor理论，气幕帘产生的最大表层流速为：

式中：K为常数；Q为单位长度开孔管单位时间内出气量，且：

其中：h0为标准大气压的水头；h为开孔管深度；Q0为相同压力下单位时间内自由出流的气量。

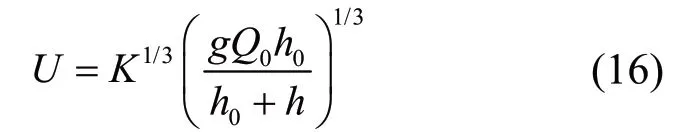
根据Taylor提出消波所需表面最大水平流速计算公式：

因此，消波所需的供气量为：

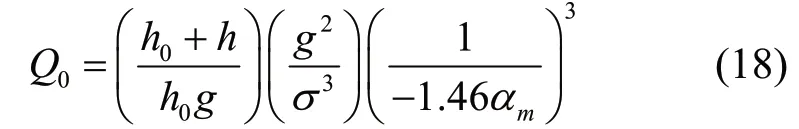
深水时，波长L=2πg/σ2，有：

根据Bulson试验结果，表层水流厚度为：

若波陡较大时，需考虑波浪非线性影响。消波所需供气量还应乘以一个放大系数β，β=2H/L+0.6。

3 气幕防波堤试验

为分析气幕防波堤消浪效果，Kurihara分别开展了小尺度物理模型试验和现场全尺度测试。小尺度试验在九州大学应用力学所的水槽中进行，水槽尺寸为1.5 m×1.5 m×60 m。全尺度测试进行了三次，第一次在长崎市岩岛，时间为1954～1955年的冬季，所用开孔管长度为30 m，孔径为1.5 mm，孔密度为35.7个/m，最大供气量为20 L/(s·m)；第二次在长崎市羽岛，时间为1955～1956年的冬季，所用开孔管长度为60.5 m，孔径为2.0 mm，孔密度为47.6个/m，最大供气量为30 L/(s·m)；第三次在横滨新日铁株式会社鹤见造船厂的码头，时间为1957年春秋两季，所用开孔管孔径为2.5 mm，孔密度为94个/m，最大供气量为75 L/(s·m)，气幕装置分别采用三种型式：A型为宽度为2.5 m的双排管、B型为宽度为1.5 m的双排管、C型为单排管。另外，鹤见造船厂码头还布置了一套永久性气幕帘装置，型式为2.0 m宽的双排管，开孔管孔径为1.0 mm，孔密度为245个/m。

试验表明，气幕防波堤产生的水平流的厚度并非常数，而是随到气幕中心的距离先减小后增加。Kurihara认为表层水流特征厚度应取能量流最大断面的厚度。现场测试显示该特征断面位于距气幕帘中心约0.7倍水深处，水流厚度的大小为：

式中：星号表示特征断面。试验也表明水平流的速度u在深度上并非呈线性分布，而是随深度z的1/2次方线性变化，即。表层最大流速U与供气量仍符合式（16），但系数1/3K并非常数，而是随到气幕中心的距离而变小。

在特征断面处，表层流速最大值为：

将表层流速沿水深分布写成如下形式：

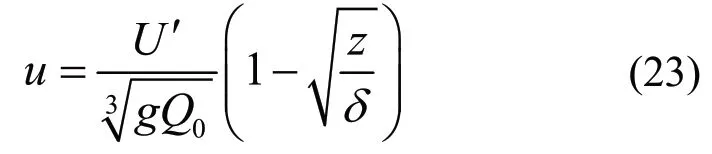
则：

定义：

ξ为描述表层气幕强度的无量纲数。Kurihara通过小尺度试验和现场测试证明，ξ*与L/δ*符合图2所示的关系。在实际应用中，采用前1/3大波的平均周期作为平均周期，平均波长则为：

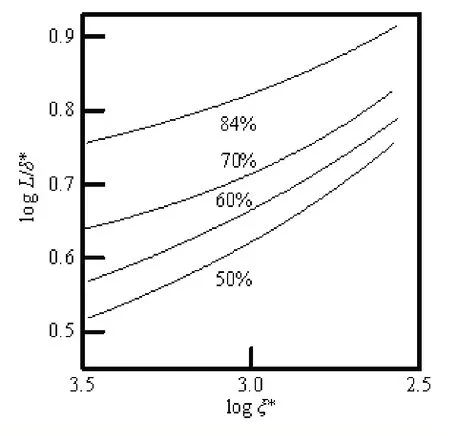
图2 不同透射系数下 ξ *与L/δ *之间的关系

4 供气量计算

首先，获得现场水文条件，包括水深、入射波平均周期等；再根据式（25）和式（21）计算平均波长L和特征水流厚度δ*；然后，根据气幕防波堤要求的透射系数，从图2中确定ξ*值；最后，根据式（22）获得气幕帘所需供气量。

5 结语

1）气幕防波堤的消波性能与供气量大小有关。

2）气幕防波堤对供气量要求较高，建议作为临时消波设施。

3）本文给出的供气量计算方法可作为气幕防波堤设计提供参考。