极差分析和小波变换在银川站气候变化趋势分析中的应用

肖云清，毛志春，谭志强，翟颖佳，张建荣

（1.中国气象局旱区特色农业气象灾害监测预警与风险管理重点实验室，宁夏银川 750002；2.银川市气象局，宁夏银川 750002；3.中国人民解放军 31682 部队，甘肃兰州 730020；4.宁夏气象台，宁夏银川 750002）

地球上几乎所有的天气和气候现象均与多时间尺度相联系，特别是气候变化，包含多种时间尺度，当前在短期气候变化方面主要研究的是月、季、年际尺度和几十年尺度的长期变化。严中伟等[1]的研究表明，气候的变化不但具有全球性，而且具有局地特征。另外，传统的分析方法一般是傅里叶分析和滤波分析，以找出气候资料中所包含的周期并与诸如太阳黑子周期等已知的周期相比较为目的，而小波分析可以通过伸缩和平移等运算功能对函数或信号序列进行多尺度细化分析，研究不同尺度（周期）随时间的演变情况。由于小波分析所具备的这种特殊的“显微镜”功能，其已成功地应用于各个领域，并成为研究气象要素长期变化的十分重要的工具[2—6]。尤卫红[7]运用Marr 小波和Morlet 小波分析了云南近百年的气温和降水变化，得出云南最近几年的气温在其较大尺度和较小尺度的变化中均处于较强的偏暖期，近几年降水在其较大尺度变化中处于一个降水的偏少期，而在其较小尺度的变化中处于一个降水的偏多期，降水变化的较大时间尺度特征与气温有比较好的对应关系。R/S 分析法是一种基于分形理论的分析方法，它可以通过分析系统对初始条件的平均记忆长度，得到过去的趋势对未来事件产生影响的时间长度，即未来这种变化所持续的时间，从而对序列未来变化作出科学预测，现在已广泛应用于气候和水文序列的变化分析中[8—11]。翟秋敏等[12]采用M-K 检验法寻找年平均气温、降水量序列的变异点，同时通过综合运用R/S分析法、小波分析法分析豫南地区气候变化的多时间尺度特征及预测未来气候的变化状况。结果表明：豫南地区年平均气温存在准30 年的主要震荡周期和准15 年的次主要周期，年平均降水量存在准15 年的主周期和准3 年、准7 年的第二主周期；近60 年来，平均气温呈现显著升高的趋势以及未来一段时间将进入到降水量偏低的时期。目前，针对银川地区气候变化的研究较多[13—17]。例如李凤琴等[18]运用银川基准站1951—2007 年气温、降水等资料，分析得出银川站的年平均气温1980年前变化比较平缓，在1980 年后迅速上升，特别是2000 年后升幅较大，降水量呈波动变化特点；刘钰等[19]利用银川站1951—2013 年气象数据，采用滑动平均、Mann-Kendall 方法及Spearman 相关系数等方法，分析了近20 年各气候要素变化和城市发展的关系。

本文利用银川站最新的降水量资料和气温资料，运用线性回归与R/S 分析法，同时结合小波分析法对银川站的气候变化特点进行分析，以期找出银川站的变化规律和多时间尺度演变特征及未来变化趋势，更好地服务于短期气候预测。

1 数据来源与方法

1.1 研究数据

本文采用银川站1961—2018 年58 年的逐年平均降水量和平均温度资料，资料来源于银川气象局逐年观测数据。

1.2 研究方法

1.2.1 线性回归与R/S 分析法 线性回归法可以定量分析气象水文序列在某一时间段内的趋势特征是否显著，Xi（i=1,2,…,n）表示某一气候变量序列，Ti（i=1,2,…,n）表示所对应的时刻，对Xi-Ti进行线性回归拟合，建立Xi与Ti的一元线性回归方程：

式中：a 为常数项；b 为回归系数，当回归系数b 大于0 时表示水文序列具有增加趋势，小于0 时表示水文序列具有减少趋势，其显著性采用t 分布进行检验。

R/S 分析法是赫斯特（H.E.Hurst）于1965 年提出的，可以定性分析水文序列过去与将来是否存在相同或相反的变化趋势，重点揭示将来的变化趋势。其主要原理如下：

设时间序列X（t）,（t=1,2,…,n），则该序列的累积离差为

式中：S（T）为n 个时间数据的标准差；H 为Hurst 指数；c 为常数。

如果点绘重标极差与时间的对数关系图（即ln（R（T）/S（T））-ln T 关系图），那么拟合直线斜率就是Hurst 指数H。该指数可以定性地说明水文序列的变化特性：0.5＜H≤1，表明序列具有持久性，即时间序列未来的变化趋势与过去的总体变化趋势相同，且值越趋近1，依赖性越强；H=0.5，说明序列是随机的，即未来的变化趋势与过去的总体变化趋势无关；0＜H＜0.5，说明序列具有反持久性，即未来的变化趋势将与过去的总体变化趋势相反，且值越趋近于0，反持久性越强。

采用线性回归与R/S 分析法对水文序列的变化趋势进行综合分析的具体做法是：由回归系数的估计值分析水文序列的变化趋势；根据H值分析水文序列的持久性或反持久性特征；然后综合两者的结果分析水文序列未来的变化趋势特征（表1）。

表1 水文序列未来趋势特征判别分析表

1.2.2 小波分析法 对于信号f（t）∈L2（R）（L2（R）表示平方可积的实数空间，即能量有限的空间信号），其连续小波变换为

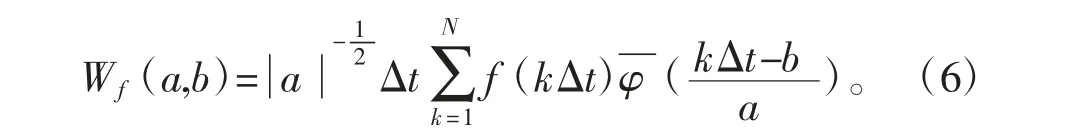
其中，Wf（a,b）是时间序列f（t）或f（kΔt）通过单位脉冲的滤波器的输出，它能同时反映时域参数b 和频域参数a 的特性。当a 较小时，对频域的分辨率低，对时域的分辨率高；当a 增大时，对频域的分辨率高，对时域的分辨率低。因此，小波变换能实现窗口的大小固定、形状可变的时频局部化，正是这个意义上小波变换被誉为数学显微镜。

小波系数的模和实部是Morlet 小波变换得到的最重要的变量。小波系数模的大小表示特征时间尺度信号的强弱，其模值越大，表明其所对应的时段和尺度的周期性越明显。Morlet 小波系数的实部包含着给定时间和尺度信号相对于其他时间和尺度信号的强度和位相两方面的信息。

2 结果与分析

2.1 平均降水量和平均温度的变化趋势分析

2.1.1 平均降水量和平均温度的年际变化 图1a是银川站逐年平均降水量、5 年滑动平均降水量及变化趋势图。由图1a 可知，1961—2018 年银川站逐年平均降水量呈现出波状分布的变化态势。从降水分布来看，20 世纪70 年代初期、80 年代初期和中期、90 年代后期银川站平均降水量相对偏少，其中1980 年、1981 年、2005 年降水量异常偏少；20 世纪60 年代初期、70 年代后期和2014—2018 年平均降水量相对偏多，其中1961 年、1964 年、1967 年、1973年、2012 年和2018 年平均降水量异常偏多。从5 年滑动平均降水量来看，20 世纪60 年代中期至70 年代初期、20 世纪70 年代后期至80 年代中期、20 世纪90 年代初期至2000 年、2000 年初至2009 年银川站逐年降水量处于减少趋势，20 世纪70 年代初期至70 年代后期、20 世纪80 年代中期至90 年代初期、2010 年后银川站逐年降水量都处于增加趋势。由计算得出线性趋势回归方程为y=0.096x+3.735，回归系数的估计值b=0.096，表明序列具有增加趋势。采用t 分布进行显著性检验，统计量0.192，小于显著水平α=0.05 的分布临界值tα[56]=2.004，说明银川站逐年平均降水量序列增加趋势不明显。

图1b 是银川站逐年平均温度、5 年滑动平均温度及变化趋势图。从整体变化趋势来看，1961—1996年银川站平均温度整体偏低，其中1967—1971 年、1976 年和1984 年异常偏低，从1997 年开始，银川站平均温度相对偏高，尤其是进入2000 年后，银川站平均温度整体异常偏高。从5 年滑动平均温度来看，银川站平均温度整体处于上升趋势，尤其是在20 世纪90 年代后期开始，平均温度上升比较明显。由计算得出线性趋势回归方程为y=0.045x-81.17，回归系数的估计值b=0.045，表明序列具有增加趋势。采用t 分布进行显著性检验，统计量大于显著水平α=0.05 的分布临界值tα[56]=2.004，说明银川站逐年平均温度序列增加趋势明显。

2.1.2 平均降水量和平均温度的年代际变化 对表2 的平均降水量年代际变化进行分析可知，银川站的年平均降水量呈现降低—升高—降低—升高的变化趋势。20 世纪60 年代降水量有减少的趋势，且降水量波动性大，离差系数达到0.45，但降水量仍相对较多，平均降水量为210.3 mm，距平为20.3 mm。20 世纪70 年代、80 年代降水量为增加的趋势，其中70 年代平均降水量增加幅度最大，为12.98 mm/10 a，降水距平为正，为13.3 mm，80 年代增加幅度为11.03 mm/10a，距平为-25.8mm。20 世纪90年代平均降水量为降低的趋势，倾向率为-7.11 mm/10 a，平均降水量为193.9 mm，距平为3.9 mm。2000 年开始降水量缓慢升高，增加幅度为0.84 mm/10 a，但降水距平仍为负，为-9.9 mm，2010—2018 年增大幅度升高，距平值开始为正，为30.7 mm。总的来看，银川站年平均降水量波动的变化特性明显，2000年以后处于波动上升过程中，与年际变化分析基本一致。

图1 银川站年平均降水量和平均温度变化趋势图

表2 平均降水量的年代际变化统计表

表3 平均温度的年代际变化统计表

表3 为银川站平均温度年代际变化。由表3 可知，银川站的年平均温度呈现先降低后升高的变化趋势。20 世纪60 年代平均温度有减少的趋势，相对平均温度偏低0.81 ℃。20 世纪70 年代开始平均温度逐渐上升，70 年代和80 年代的气候倾向率分别为0.096 ℃/10 a 和0.016 ℃/10 a，相对平均温度分别偏低0.78 ℃和0.53 ℃，90 年代以后开始为正距平，相对平均温度分别偏高0.11 ℃、0.84 ℃和1.20 ℃，距平幅度越来越大，2010 年以后平均温度达到10.5 ℃。从温度变化来看，20 世纪90 年代升温幅度最大，达到0.11 ℃/10 a，同时90 年代温度波动较大，离差系数达到0.071。总体来看，20 世纪70 年代后银川站年平均温度处于上升趋势，波动变化较小。

2.2 运用线性回归和重标极差（R/S）分析

基于R/S 分析原理，对银川站平均降水量进行Hurst 指数计算，并通过一元线性回归对ln（R（T）/S（T））-ln T 的趋势线进行拟合，拟合结果见图2a，可以得到Hurst 指数（趋势线斜率）及相关拟合参数。从计算结果来看，拟合直线方程为y=0.537 1x-0.340 2，Hurst 指数为0.537 1，Hurst 指数大于0.5，表明未来的变化趋势与过去的总体变化趋势相同，决定系数R2为0.942 2，统计量大于显著水平α=0.05 的分布临界值tα[56]=2.004，拟合效果相对较好，表现出一定的增加趋势。

图2b 为平均温度的一元线性回归的ln（R（T）/S（T））-ln T 趋势线。从计算结果来看，拟合直线方程为y=0.919 4x-0.811 9，Hurst 指数为0.919 4，即时间序列未来的变化趋势与过去的总体变化趋势相同，且接近于1，表明依赖性越强；决定系数R2为0.953 3，统计量，远远大于显著水平α=0.05 的分布临界值tα[56]=2.004，拟合效果比较好，增加趋势明显。

图2 银川站年平均降水量和平均温度的Hurst 指数分布图

综合分析可以得到，银川站逐年平均降水量回归系数估计值b=0.096，表明序列具有增加趋势，同时得到Hurst 指数为0.537 1，大于0.5，根据表1 分析得到，银川站年平均降水量在未来会有弱的增加趋势。

银川站平均温度回归系数估计值b=0.045，表明序列具有增加趋势，同时得到Hurst 指数为0.919 4，远远大于0.5，且接近于1，根据表1 分析得到，银川站平均温度在未来会有持续增加趋势，且依赖性强。

2.3 小波变换分析

图3a 绘制了银川站逐年平均降水量Morlet 小波变换系数模平方的时频变化，可以看出不同时段各时间尺度的强弱变化特征。由图3a 可知，银川站逐年平均降水量主要有2～4 年、4～6 年、10～15 年3种时间尺度变化较强，其余尺度表现相对较弱。其中2～4 年时间尺度主要发生在1961—1975 年、1990—1996 年、2010—2015 年，而1961—1975 年时间段内振荡中心比较明显，大约在1964 年，其他2 个时段振荡中心不明显；4～6 年时间尺度主要发生在1965—1990 年、2000—2010 年，振荡中心分别在1980 年和2005 年；10～15 年时间尺度主要发生在1961—1995 年，振荡中心在1980 年左右。同时，从图3a 可以看到，在1961—1995 年35 年的时间区段内主要包含着2～4 年、4～6 年、10～15 年3种时间尺度，即银川站逐年平均降水量在时域变化上不是以一种时间尺度变化，而是包含着多种时间尺度。

图3b 为银川站逐年平均降水量Morlet 小波变换实部的时频变化。图3b 清晰地显示了银川站逐年平均降水量时间尺度变化特点、突变点分布及其相位结构。其中10～15 年尺度表现十分明显，其中心时间尺度为12 年左右，正负相位交替出现；1961—1966 年、1974—1979 年、1987—1992年、1999—2005、2012—2018 年各时段为正相位，表示降水量偏多，而1967—1973、1980—1986 年、1993—1998 年、2006—2011 年各时段为负相位，表示降水偏少；突变点出现在1967 年、1974 年、1980年、1987 年、1993 年、1999 年、2006 年和2012 年，且2012 年后银川站年平均降水量依然处于正相位中。总体来看，银川站逐年平均降水量在2018 年以后的时间段内降水的时间尺度表现不是很明显，但从实部的时频变化来分析，未来银川站平均降水量处于正相位中，表明降水量仍然偏多。

图4a 绘制了银川站逐年平均温度Morlet 小波变换系数模平方的时频变化。由图4a 可知，银川站逐年平均温度变化主要有3 种时间尺度，分别是8年、25 年和60 年左右。其中8 年左右的时间尺度主要发生在1985—1995 年；25 年左右的时间尺度主要发生在1965—2018 年；60 年左右的时间尺度最强烈，主要发生在1961—2018 年整个研究时间段内，振荡中心在1995 年左右。同时从图上可以看到，在1961—2018 年时间段内包含着25 年和60 年左右2 种时间尺度，其中60 年左右的时间尺度表现比较明显。

图4b 为银川站逐年平均温度Morlet 小波变换系数实部的时频变化。图4b 中清晰地显示了银川站平均温度的时间尺度变化特点、突变点分布及其相位结构。其中60 年左右的尺度表现十分明显，正负相位交替出现。可以看出，1961—1991 年为负相位，表示平均温度偏低，1992 年以后为正相位，表示平均温度偏高，突变点在1992 年。而25 年尺度表现也相对明显，正负相位也交替出现，但相对60 年的时间尺度来说，已表现得不是很突出。

总体来看，银川站逐年平均温度在2018 年以后的时间段内会以60 年作为其变化的主要时间尺度，从实部的变化趋势来分析，未来银川站还会处于平均温度相对较高的尺度周期内。

综合线性回归、重标极差（R/S）和Morlet 小波分析结果，银川站年平均降水量在2018 年后会持续弱的增长趋势，但同时其降水量变化的波动性也比较明显，而银川站平均温度在2018 年后还会有持续增温趋势，这与李凤琴等[18]、刘钰等[19]的研究结果基本一致。

图3 银川站逐年平均降水量Morlet 小波变换模平方和实部时频变化特征图

图4 银川站逐年平均温度Morlet 小波变换模平方和实部时频变化特征图

3 结论

本文利用线性回归、重标极差（R/S）和Morlet 小波分析法对银川站逐年平均降水量和平均温度进行分析，得出以下结论：

（1）1961—2018 年银川站逐年平均降水量呈现出波状分布的变化态势。20 世纪70 年代初、80 年代初期和中期、90 年代后期银川站平均降水量相对偏少，20 世纪60 年代初、70 年代后期和2014 年后降水量相对偏多。从5 年滑动平均来看，银川站也是明显处于波动变化过程。从平均降水量年代际变化进行分析，银川站的年平均降水量呈现降低—升高—降低—升高的变化趋势。

（2）银川站平均温度变化明显，1961—1996 年平均温度整体偏低，1997 后平均温度偏高，尤其进入2000 年后，银川站平均温度整体异常偏高。从5年滑动平均来看，银川站平均温度整体处于上升趋势；从年代际变化分析来看，银川站的年平均温度呈现先降低后升高的趋势，2010—2018 年平均温度达到10.5 ℃，而且在1990—1999 年温度波动较大。

（3）银川站逐年平均降水量表现出周期变化的多样性。1961—1995 年35 年的时间区段内主要包含着2～4 年、4～6 年、10～15 年3 种时间尺度，其中10～15 年尺度表现十分明显，其中心时间尺度为12年左右。

（4）银川站平均温度在1961—2018 年时间段内包含着25 年和60 年左右2 种时间尺度，而且60 年左右的时间尺度表现比较明显。

（5）结合线性回归、重标极差（R/S）和Morlet 小波分析，银川站年平均降水量在未来会持续弱的增长趋势，但波动性特征明显。银川站平均温度在2018 年后还会持续增温趋势。