割压联合作用下钻孔塑性区范围分布研究

周应江，刘怀付，汪有清，张永将，徐遵玉

(1.中煤新集能源股份有限公司，安徽 淮南 232001； 2.中煤科工集团重庆研究院有限公司，重庆 400037；3.瓦斯灾害监控与应急技术国家重点实验室，重庆 400037)

钻孔预抽瓦斯是防治煤与瓦斯突出的重要手段。针对钻孔卸压增透机理、钻孔孔壁弹塑性分析，众多学者对此进行了深入的研究。杜春志等[1]通过弹塑性力学理论分析了钻孔周围应力和卸压区范围,利用RFPA模拟软件，得出卸压区半径随着钻孔孔径的增大而增大的影响规律；许胜军[2]基于D-P准则和UDEC数值模拟对钻孔稳定性进行研究，结果表明随着节理密度的增大，钻孔周边剪切位移呈指数增加，钻孔首先在孔壁处发生拉伸破坏，且随着煤体沿径向向深部转移，钻孔周围的煤体逐渐发生剪切破坏；郝富昌等[3]基于M-C强度准则，建立塑性软化和扩容的黏弹塑性模型，推导了应力、位移及卸压范围解析式，对比分析了软硬煤层钻孔的应力分布及卸压效果，研究了抽放钻孔孔径变化规律；韩颖等[4]基于H-B准则、地质强度指标(GSI)与岩石断裂力学理论，分析了钻孔周围“三带(区)”内孔壁稳定性，指出卸压带易垮孔，峰后应力集中带易喷孔、顶钻，峰前应力集中带的孔壁失稳破坏的概率较低；姚向荣等[5]利用FLAC3D软件对钻孔进行数值分析，得出位移场、应力场和塑性破坏区变化规律，分析了钻孔稳定性影响因素；蔺海晓等[6]利用UDEC数值模拟软件分析了多种因素对煤层钻孔周边应力场的影响。

水力化煤层增透卸压技术是提高瓦斯抽采效果的重要技术之一，如水力压裂[7-10]、水力割缝等[11-14]。为更好实现卸压增透，部分学者将水力割缝和水力压裂技术结合，闫发志等[15]采用数值模拟的方法，分析了割缝钻孔与压裂钻孔协同布置时压裂裂缝扩展规律，得出协同割缝钻孔和协同压裂钻孔的瓦斯抽采纯量分别是割缝钻孔的2.3倍和2.1倍，是普通钻孔的7.8倍和5.0倍，瓦斯抽采效率显著提高；黄炳香等[16]进行了坚硬顶板钻孔预割缝定向水力致裂的半工业性试验，得出裂缝沿预割缝槽优先起裂；王耀锋等[17]基于定向水力压裂的定向理论及预置导向槽定向水力压穿增透作用机理，提出水力压穿增透新工艺，有效实现了煤层的卸压和增透；李艳增[18]等先进行水力割缝扩大钻孔直径，再进行水力压裂使煤体周围产生更多裂隙，钻孔影响范围增大，瓦斯抽采排放效率得到大幅度提高，抽放钻孔数量减少，成本大大降低。

笔者采用统一强度理论，考虑峰后软化和中间主应力的影响，推导出超高压水力割缝和水力压裂联合作用下钻孔孔径的变化和塑性区半径分布解析式，结合具体算例，分析了相关参数对塑性区范围的影响，所得结果可为矿井解决低透气性煤层抽采治理瓦斯技术难题提供一定的理论依据和参考。

1 理论分析模型

1.1 力学模型

煤体在超高压水力作用下，当钻孔周围煤体超过自身强度时，孔壁由内向外依次为塑性软化区和弹性区[19]，钻孔力学模型如图1所示。

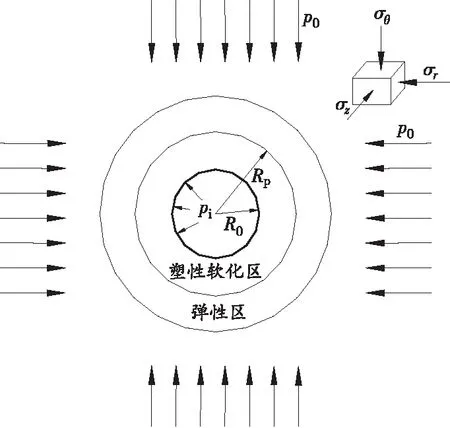
图1 钻孔力学模型

模型假设如下：

1)钻孔受原岩应力p0作用，侧压系数λ=1，按轴对称问题处理，简化为平面应变；

2)钻孔周围煤体均匀、各向同性，不考虑钻孔卸压对钻孔的影响；

3)R0为钻孔半径，Rp为塑性区半径，σp为峰值强度，σc为残余强度，水力压裂压力pi均匀作用在钻孔孔壁处。

1.2 统一强度准则

假定压应力为正，拉应力为负，深部钻孔受到地应力作用，此时有：σ1=σθ，σ3=σr，σ2=σz=μ(σθ+σr)。采用统一强度理论描述钻孔孔壁弹塑性状态的强度特征，表达式如下[20]：

σθ=Ajσr+Bj

(1)

(2)

式中：σθ、σr分别为钻孔孔壁的切向应力、径向应力，MPa；Aj、Bj为煤体表征参数，表示最大主应力和最小主应力之间的关系；μ为泊松比；j为符号参数，当j=e时，φe为煤体初始内摩擦角，(°);Ce为煤体初始黏聚力，MPa;当j=p时，φp为塑性软化区内摩擦角，(°);Cp为塑性软化区黏聚力,MPa；b为中间主应力系数，0≤b≤1。

1.3 软化模型

在应力—应变曲线中，当煤体的强度超过其极限强度后会发生破坏，假设残余摩擦角φc和残余黏聚力Cc不变；当煤体的强度超过其峰值强度时会发生塑性软化，塑性区内摩擦角φp和黏聚力Cp的值随着塑性应变的增加而逐渐减小，假定φp和Cp与初始内摩擦角φe和黏聚力Ce呈线性软化关系，引入软化系数kφ和kC，则有：

(3)

(4)

式中：kφ为内摩擦角软化系数；kC为黏聚力软化系数；φc为残余内摩擦角，(°)；Cc为残余黏聚力，MPa；Rp为塑性区半径，m。

2 孔周弹性区和塑性区分析

2.1 弹性区应力场

钻孔煤体处于线弹性状态下，设py为煤体弹性区与塑性软化区交界处径向应力，煤体弹性区视为受py和地应力p0共同作用下的厚壁圆筒，可知弹性区应力为：

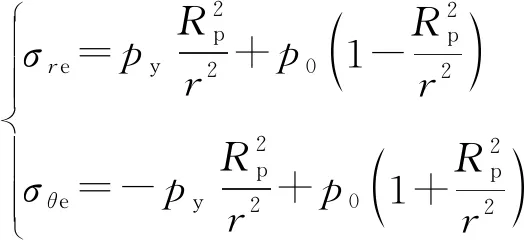
(5)

式中：σre为弹性区径向应力，MPa；σθe为弹性区切向应力，MPa；r为煤体内任意一点到圆心的距离，m；p0为地应力，MPa；py为弹塑性交界处的应力，MPa；Rp为塑性区半径，m。

在弹塑性交界r=Rp处，式(5)满足式(1)且径向应力连续，整理可得：

(6)

2.2 塑性区应力场

煤体中任一研究单元点满足平衡微分方程：

(7)

将式(1)代入式(7)并进行积分，以σr|r=R0=pi为边界条件，可得塑性区径向应力和切向应力为:

(8)

径向应力σr在弹塑性交界处连续，即σrp|r=Rp=σre|r=Rp。联立式(8)第一式和式(5)第一式可得塑性区半径为:

(9)

3 算例分析

水力割缝、水力压裂联合卸压增透技术，是利用已完成的小直径穿层钻孔进行水力割缝，扩大煤孔段直径，然后进行水力压裂增加煤层裂隙的割压联合技术。以新集二矿1煤组为例，原岩垂直应力和水平应力分别为13.8、11.7 MPa，取p0=12 MPa，施工钻孔直径为113 mm，煤层泊松比μ=0.23，初始内摩擦角φe=30°，残余内摩擦角φc=10°，初始黏聚力Ce=2.5 MPa，残余黏聚力Cc=0.5 MPa。

新集二矿220112工作面累计施工11个割缝钻孔，割缝数量4～17刀，单刀割缝时间3 min，单孔割缝时间40～100 min，平均时间60 min，出煤量1.2～5.0 t，单孔平均排屑量为2.3 t，平均每刀排屑量为0.32 t。孔段割缝间距为1.5 m。根据式(10)可计算割缝半径：

(10)

式中：rg为割缝后缝隙的半径，m；m为割缝后排出的煤屑量，t；h为割缝后裂隙高度，根据地面试验割缝后产生裂隙高度一般为0.008～0.010 m，取0.010 m；K为割缝后产生煤屑的碎涨系数，一般K=1.1～1.3，取K=1.2；γ为煤的密度，新集二矿1煤层密度γ为1.42 t/m3。

将割缝的缝隙视为一个圆柱体，根据公式(10)可计算出割缝后形成缝槽半径为2.45 m，是未割缝前钻孔直径的43.4倍。

将式(10)代入式(9)即可求出钻孔割压联合作用下的塑性区半径Rp的分布规律。

通过分析各个参数下塑性区半径Rp的变化，得出参数变化对塑性区半径Rp的影响规律。

1)中间主应力系数b对钻孔在不同情况下塑性区半径Rp分布的影响曲线如图2所示。

图2 kφ=1和kC=1时,塑性区半径Rp与中间主应力系数b的关系

由图2可知：在钻孔正常施工(不考虑水力割缝、水力压裂，下同)和超高压水力割缝情况下，塑性区半径Rp均随中间主应力系数b的增大而逐渐增大；当b=0时Rp分别为0.041、1.780 m，而当b=1时Rp分别为0.047、2.050 m，分别增加了14.6%、15.2%。割缝后再进行压裂(压裂压力pi=20 MPa)，塑性区半径Rp随着中间主应力系数的增大几乎不变，约为4.220 m，比超高压水力割缝(b=0)时增大了1.37倍。

采用超高压水力割缝和压裂联合卸压增透技术后，塑性区范围大幅度增加，但随着中间主应力系数的增大几乎不变。

2)内摩擦角软化系数kφ对钻孔在不同情况下塑性区半径Rp分布的影响曲线如图3所示。

图3 b=0.5和kC=1时，塑性区半径Rp与内摩擦角

由图3可知：钻孔正常施工和超高压水力割缝情况下，塑性区半径Rp随内摩擦角软化系数kφ的增大而增大；当kφ=1/3时Rp分别为0.018、0.761 m，而当kφ=1时Rp分别为0.023、0.976 m，分别增加了27.8%、28.3%。割缝后再进行压裂(压裂压力pi=20 MPa)，塑性区半径Rp随着内摩擦角软化系数的增大而逐渐减小，当kφ=1/3时Rp为9.456 m，而当kφ=1时Rp为4.472 m，减小了52.7%。当kφ=1/3、kφ=1/2、kφ=2/3、kφ=5/6、kφ=1时，割压联合后塑性区半径比割缝后分别增加了11.42、8.85、6.65、4.92、3.58倍。

内摩擦角软化系数kφ对塑性区范围具有显著的影响，相比于超高压水力割缝，煤体在割缝后再进行压裂，钻孔塑性区范围会有很大程度的增大。

3)黏聚力软化系数kC变化对钻孔在不同情况下塑性区半径Rp的影响曲线如图4所示。

图4 b=0.5和kφ=1时，塑性区半径Rp与黏聚力

由图4可知：钻孔正常施工和超高压水力割缝情况下，塑性区半径Rp随kC的增大而增大；当kC=1/5时Rp分别为0.010、0.435 m，而当kC=1时Rp分别为0.023、0.976 m，分别增加了130.0%、124.4%。割缝后再进行压裂(压裂压力pi=20 MPa)，塑性区半径Rp随着kC的增大而减小，当kC=1/5时Rp为4.541 m，而当kC=1时Rp为4.472 m，减小了1.52%。当kC=1/5、kC=2/5、kC=3/5、kC=4/5、kC=1时，割压联合后塑性区半径比水力割缝分别增加了9.45、6.29、4.93、4.12、3.58倍。

考虑黏聚力软化系数kC对塑性区范围具有显著的影响，相比于超高压水力割缝，煤体在割缝后进行压裂钻孔塑性区范围会有较大程度的增大。

4)压裂压力pi对钻孔塑性区半径Rp的影响曲线如图5所示。

图5 kφ=1和kC=1时，塑性区半径Rp与压裂压力pi的关系

由图5可知：在中间主应力一定(b=0.5)和不考虑煤体软化，压裂压力分别为0、5、10、15、20、25、30 MPa时，塑性区半径分别为0.98、2.34、3.19、3.88、4.47、5.00、5.48 m。随着压裂压力pi的增大，塑性区半径逐渐增大，整体看来，塑性区半径与压裂压力大致呈正相关关系，塑性区半径与压裂压力的拟合公式为Rp=0.143 8pi+1.463 5(R2=0.965 3)。

4 结论

1)基于统一强度理论，引入内摩擦角软化系数kφ和黏聚力软化系数kC，考虑峰后软化和中间主应力等综合影响，深入研究了钻孔在超高压水力割缝和水力压裂联合作用下的塑性区范围分布规律。

2)钻孔正常施工(不考虑水力割缝、水力压裂)和超高压水力割缝情况下，塑性区半径Rp随中间主应力系数b、内摩擦角软化系数kφ、黏聚力软化系数kC的增大逐渐增大。

3)采用割压联合技术后，塑性区半径Rp随着中间主应力系数的增大几乎不变，比采用超高压水力割缝(b=0)时增加了1.37倍；塑性区半径Rp随着kφ和kC的增大而逐渐减小，比采用超高压水力割缝时最大分别增加了11.42倍和9.45倍。

4)在超高压水力割缝的基础上，随着压裂压力的增大，钻孔塑性区半径均有不同程度的增加，整体看来，塑性区半径与压裂压力大致呈正相关关系，在压力为30 MPa时塑性区范围为5.48 m。