时标上高阶动力系统的Lyapunov型不等式*

周 欣, 张启明， 张明欢

(湖南工业大学理学院，湖南 株洲 412000)

0 引 言

时标是指实数集上的任一非空闭子集. Higer教授[1,2]于1988年首次提出时标的概念，并建立了一些时标理论.此后，时标理论在文献[1-2]的基础上蓬勃发展.其中，M.Bohner和A.Peterson在文献[3-4]中，研究了时标上的一类非常重要的动力系统：时标动力系统.此系统不仅包括微分和差分两种特殊情形，而且在应用上也很广泛.其理论研究主要集中在边值问题、振动性、稳定性、非共轭性等方面[5-6].研究时标上的Lyapunov型不等式有助于完善微分和差分系统中的相关结论.

1 预备知识

近年来，很多学者给出了几类高阶动力系统的Lyapunov型不等式，对于满足某些边值条件的Lyapunov型不等式的结果也较多，例如：

2010年，Cakmak[7]研究了满足条件(2)的2n阶微分系统

x2n(t)+q(t)x(t)=0

(1)

x2i(a)=x2i(b)=0,i=0,1,…,n-1

(2)

的Lyapunov型不等式，并得到如下结论：

定理1[7]若x(t)是系统(1)的解，满足条件(2)且x(t)≠0,t∈(a,b)，则

(3)

2012年，Youyu Wang[8]研究了满足条件(5)下的高阶微分系统

(|xm(t)|p-2xm(t))′+

r(t)|x(t)|p-2x(t)=0,t∈(a,b)

(4)

xi(a)+xi(b)=0,i=0,1,2,…,m

(5)

的Lyapunov型不等式，并得到如下结论：

定理2[8]若x(t)是系统(4)的非零解，满足条件(5)，则

(6)

受文献[7]和[8]的启发，分别探讨了满足边值条件(7)和条件(8)时

xΔi(a)=xΔi(b)=0,i=0,1,…,m-1

(7)

xΔi(a)+xΔi(b)=0,i=0,1,…,m-1

(8)

高阶动力系统(9)

(f(t)|xΔm-1(t)|p-2xΔm-1(t))Δ+

r(t)|x(t)|p-2x(t)=0

(9)

的Lyapunov型不等式，其中m≥2.

2 主要结论及证明

引理3.1 设x(t)是系统(9)的解，满足x(t)≠0,t∈(a,b)条件(7)，其中i=0,1,…,m-1，则

(10)

证明由xΔi(a)=xΔi(b)=0，可得

(11)

(12)

那么，

(13)

(14)

结合(13)和(14)，再利用Holder’s不等式，得

(15)

故

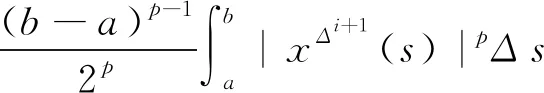
(16)

对不等式(16)左右两边积分，可以得到

(17)

即上述结论成立.

引理3.2 设x(t)是系统(9)的解，满足x(t)≠0,t∈(a,b)和条件(7)，则

|x(t)|p-1|xΔm-2(t)|≤

(18)

证明由(15)和(16)，可得

(19)

(20)

(21)

由(20)和(21)，可得

(22)

所以，

(23)

从而，由(19)和(23)可得(18)，即上述结论成立.

定理3.1 设x(t)是系统(9)的解，满足条件(7)且x(t)≠0,t∈(a,b)，f(t)为单调不减的非负函数,r(t)≠0，则

(24)

证明用xΔm-2(σ(t))乘系统(9)的两边并积分，得

(25)

由引理3.2和系统(9)，并利用分部积分公式，可得

(26)

再由(25)和(26)，得

(27)

从而，由(26)和(27)可得

(28)

故

(29)

即上述结论成立.

注1 设x(t)是系统(9)的解，满足条件(7)，且x(t)≠0,t∈(a,b)，f(t)=1，则

(30)

注2 在注1中，如果T=R,m=2n,p=2，则上述结论退化为定理1.

下面探讨动力系统(9)在条件(8)下的Lyapunov型不等式.

引理3.3 设x(t)是系统(9)的非零解，满足条件(8)，则

(31)

证明定义函数：

(32)

由条件(8)，得

(33)

并利用Holder’s不等式，可得

(34)

即

(35)

对(35)式进行积分，得

(36)

因此，(31)式成立.显然在引理3.3的条件下，引理3.2的结论也是成立的.

定理3.2 设x(t)是系统(9)的非零解，满足条件(8)且xΔi(σ(t))恒不为零，f(t)为单调不减的非负函数，r(t)≠0，则(24)式仍然成立.

证明由分部积分公式及条件(8)，对(25)式中前半部分进行化简，得

f(a)(-xΔm-1(a)|xΔm-1(a)|p-2(xΔm-2(a)+

(37)

利用(27)和(37)，可得

(38)

下面，证明

(39)

反设，上式等于零，则必有xΔm-1(σ(t))=0,t∈T.根据(9)，得到x(σ(t))=0，t∈T，与xΔi(σ(t)),i=0,1,…,m-1恒不为零矛盾，说明(39)成立，从而(24)成立.

注3 若T=R,f(t)=1，则定理3.2退化为定理2.