Y型微混合器内流流场移动粒子半隐式法数值分析

王锋,孙中国,刘启新,张凯,席光

(西安交通大学能源与动力工程学院,710049,西安)

微型混合器通常指整体尺寸在毫米级或微米级的混合器,其在细胞裂解、微物质搅拌混合、芯片散热以及高能炸药制备等工业过程中起着重要的作用。较小的尺寸在精确控制混合室内部流动的同时可提供较大的表面积比,从而实现高效混合以及强化换热。传统混合器由于安全因素,往往不能进行连续生产,须在搅拌结束后重新卸料、装料继续混合,限制了混合效率。微混合器常常集成在仅有几厘米的芯片上,由外加磁场等无接触式动力驱动,具有较高的安全性,易于实现连续化生产。

由于微混合器整体尺寸较小,雷诺数常在100以下,流动以层流为主,主要通过局部二次流形成漩涡来增强流体间的掺混与返混。常用数值仿真方法有多重参考系法、滑移网格法以及动网格法等。Khoshmanesh等采用滑移网格法研究了T型进口双叶片微搅拌器内转速对混合率的影响,发现转速过高会使混合恶化[1]。He等针对用于培养藻类的微生物混合器,利用离散相模型研究了轴向螺旋叶片对混合器内藻类流动和生长的影响并通过实验进行了验证[2]。

上述传统网格法在处理混合器内部大变形流动时容易出现网格畸变,在追踪混合界面、描述掺混机理方面存在一定困难。粒子法作为一种基于拉格朗日坐标系的CFD方法,完全摆脱了网格约束,已应用到混合现象的研究中。Laurent利用离散元方法(DEM)研究了长直圆管内轴向旋转叶片对管道内颗粒混合的影响[3]。Kwon等采用光滑粒子水动力学法(SPH),通过将固体与液体分别离散为不同物性的粒子,仿真了在旋转圆柱搅拌作用下,固体沉淀物在方腔中与液体的混合情况[4]。Shamsoddini等利用不可压缩SPH方法研究了圆柱形转子驱动的微泵混合器内流动[5]。

由于方法本身的局限性[1-2]或一些计算和假设条件过于简化[3-5],造成了以上计算结果与实际情况之间仍存在不小偏差,尤其是对常用的Y型主动式微混合器的流动机理仍然缺乏准确的解释。因此,有必要利用无网格法的优势,针对该种微混合器内实际的混合情况,进行精细化建模和研究。

本文基于移动粒子半隐式(MPS)方法,针对一种典型Y型双进口带叶片主动微混合器,提出了一种可描述局部理想有序混合的混合率定义,建立了进出口模型,对其内流混合机理进行模拟并对重要参数开展分析。

1 数值方法

1.1 控制方程

MPS法用于模拟不可压缩流动,质量守恒方程与动量守恒方程如下

(1)

(2)

式中:ρ为流体密度;u为流体速度;p为压力;μ为动力黏度;f为体积力。

1.2 粒子间作用模型

MPS法将计算区域离散为带有物性、流动以及热力学参数的粒子,通过粒子间相互作用,离散控制方程中的各项微分算子,导出梯度算子和拉普拉斯算子的光滑近似式,计算各时间层粒子的流动参数,随时间推进获取动态整场流动信息。

粒子间作用强弱可用核函数描述,本文采用的核函数[6]如下

(3)

式中:r=|ri-rj|为两粒子i、j之间距离;re为光滑半径。

梯度算子与拉普拉斯算子可通过空间泰勒展开结合光滑近似公式求得,具体推导过程可见文献[7]。为保证动量守恒,采用改进后梯度公式[8]。梯度算子与拉普拉斯算子计算公式如下

(4)

(5)

式中:φ是任意标量函数;d=2为维度;n0是粒子数密度常数。在忽略连续域内核函数截断误差的情况下,拉普拉斯算子可简化为[9]

(6)

(7)

1.3 不可压缩模型

MPS法基于粒子数密度的偏移与修正来构造不可压缩模型,粒子数密度定义如下

(8)

在拉格朗日框架下,将一个时间步分为显式估算与隐式修正两个过程。显式计算黏性力以及体积力,得到粒子位移、速度的估算值,由此位移值估算粒子数密度n*,利用该估算值结合质量守恒、动量守恒方程推导出压力泊松方程[10],由此方程隐式计算出压力,求得压力梯度力,从而修正粒子的各项参数。

采取散度自由条件法[11]构造压力泊松方程,引入伪可压系数γ,压力泊松方程如下

(9)

1.4 充分发展速度进口模型及验证

微混合器中管道长度通常远大于混合室直径,管内流体一般已达到充分发展,在叶片旋转作用下会形成弧形拉伸混合,因此有必要建立充分发展速度进口模型。

1.4.1 充分发展速度进口模型 基于移动速度进口边界条件[12],在进口起始段设置速度固定区域,该区域内粒子参与压力泊松方程计算并获取压力。速度设置为定值,进入计算区域后的粒子参与正常流体计算。考虑到充分发展速度进口边界条件相较于均匀速度进口边界条件,进口粒子的速度不均一,本文采取划分进口单元格的方式添加进口粒子,如图1所示。

图1 充分发展速度进口模型示意图Fig.1 Concept of the fully developed velocity inlet model

在每个时间步依次判断进口单元格内是否为空,若为空则添加新的进口流体粒子。

1.4.2 进口速度验证与分辨率试验 为保证流入混合器时流场速度分布满足充分发展速度模型,选取直径为1 mm的二维直管道进行验证。管内流体运动黏度为1×10-5m2/s,密度为1 000 kg/m3,进口速度为0.119 m/s。在距进口0.2 mm处设置垂直于主流方向的若干测点。选取4种分辨率0.03、0.04、0.058、0.09 mm进行计算,结果如图2所示。随着粒子直径的减小,仿真值与理论值越来越接近。考虑到计算量因素,本文选取粒子直径为0.04 mm。

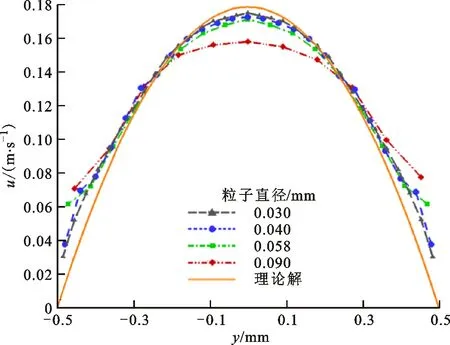
图2 不同粒子直径下管内速度分布与理论解对比Fig.2 Comparison of velocity profile between theoretical and simulation results with different particle sizes

2 数值模拟

2.1 二维Y型入口微混合器模型的建立

微混合器相关参数如表1所示。叶片静止算例的计算结果与实验[13]比较如图3所示。考虑转子转速较高,混合室内局部韦伯数达7.35,本文忽略表面张力影响。

对比可知,进口Y型尖角处以及出口管道处的两液体交界线位置与实验基本一致。实验结果中虚线圆内存在上层通道流入的蓝色液体,考虑是实验叶片底部与容器间存在间隙所致。

表1 微混合器相关参数

(a)MPS仿真结果 (b)实验结果[13]图3 叶片静止算例计算结果与实验对比Fig.3 Results comparison between MPS and experiment without rotation of blade

2.2 斜置正矩形法进口模型

传统进口模型多为水平或竖直进口,斜向进口考虑较少,本文针对任意角度斜向进口提出了斜置正矩形法进口边界模型。正矩形是指长、宽分别与坐标系的x、y轴平行的矩形,如图4所示。正矩形格的右下角位于第二列粒子中心,通过选取合适的单元格尺寸,构造可正好包裹进口粒子添加点的矩形判断单元格,以位置判断代替直线方程求解[14],可明显简化编程并提升通用性。斜置正矩形格与第二列流体粒子一一对应,与分辨率无关。

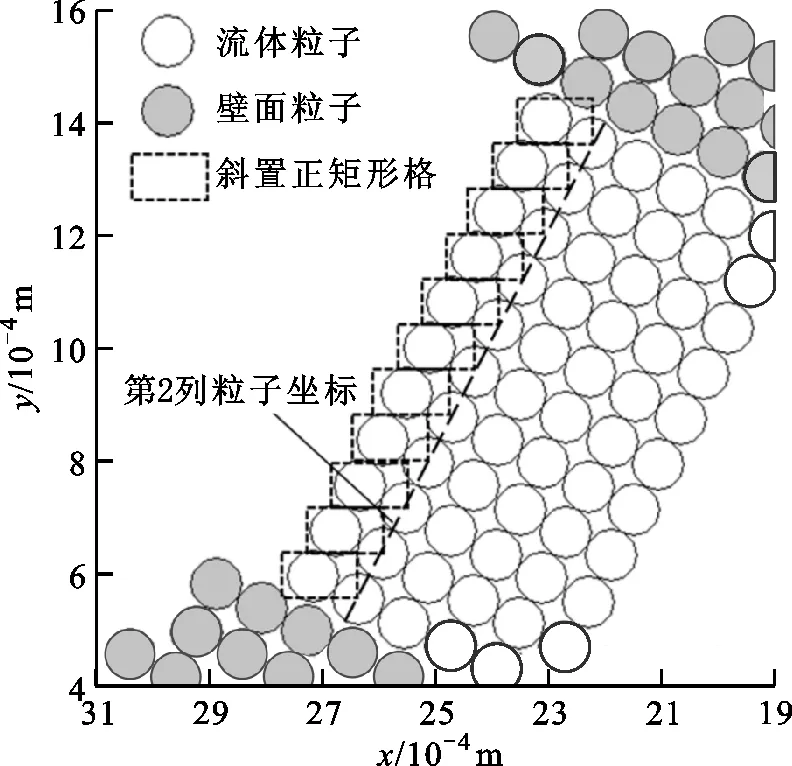
图4 斜置正矩形法进口模型示意图Fig.4 Concept of inclined continuous inlet model

3 结果与分析

3.1 混合率定义及影响因素

混合可分为理想有序混合与完美随机混合[15]。完美随机混合指在一定范围内,如一个单元格内,两种液体的浓度达到要求的比率;理想有序混合指在此的基础上,每一个流体微团附近都是与其不同种类的流体微团。

在网格法中,常通过求解浓度方程,计算出某一范围内的局部浓度,对各处的局部浓度取算数平均得到全局的浓度,利用该全局浓度与完美混合时的浓度之间的偏差结合统计学方法构造混合率。

该种方法很难描述理想有序混合,尤其是对于图5描述的情况,传统网格法求解出的混合率为100%,但实际上仍存在一定的未混合流体团,计算值未能准确描述混合情况。

图5 两液体混合特殊情况 Fig.5 The special situation of two-liquid mixing where traditional calculating method of mixing leads to wrong results

本文基于粒子法的拉格朗日特性,结合文献[16]中的交界粒子法以及传统的单元格法,在出口管道垂直主流方向设置n个单元格测点,定义了一种描述出口局部理想有序混合的混合率计算方法

(10)

(11)

式中:cs为交界线粒子个数;rs取1.4l0。当某单元格内出现明显均匀分层时,εi通过缩小xi参与标准差计算的数值来减小混合率,避免错误估计。改进后混合率计算结果与传统网格法混合率计算结果对比如图6a所示。改进前后计算出的混合率存在一定差异,尤其是当两流体的分界线经过某一混合率测量单元格时(如图6b所示,此时液体分界线经过从上至下数第2个测量单元格),传统法计算混合率为100%,与实际不符。

(a)混合率随时间的变化 (b)t=307.58 ms时液体分布图6 改进后混合率计算结果与传统混合率计算结果对比Fig.6 Comparison of results between the improved mixing calculation method and the traditional one

改进后的混合率计算方法由于修正系数εi的作用,修正了该类单元格内混合率的计算数值,使得整体混合率计算更加稳定和合理。

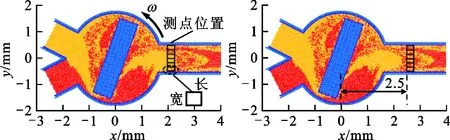
此外,本文针对混合率测点位置、测量矩形单元格宽度和长度等因素展开研究。如图7所示:长度定义为单元格沿流动方向的尺寸,宽度定义为单元格沿垂直流动方向的尺寸,测点位置定义为单元格左边界所在位置;在测量矩形格宽度为0.167 mm的情况下研究测点位置的影响,以测点矩形格左边界为基准,设置4个测点,测点坐标依次为2、2.5、3、3.5 mm。

(a)测点位置2 mm (b)测点位置2.5 mm

(c)测点位置3 mm (d)测点位置3.5 mm图7 混合率计算单元格长度、宽度定义以及测点布置 Fig.7 Measuring cells’ length, width and position for calculating mixing index

测试结果如图8所示,在t=0.135 s时出口管道处的混合率已呈现周期性波动。测点位置为2、2.5、3、3.5 mm时,混合率-时间曲线形状基本一致,仅曲线相位发生延后。混合率测点每后移0.5 mm,M-t曲线的相位后移约1.834 ms,可见测点位置的变化对混合率本身影响不大。因此,本文暂不考虑测点位置对混合率的影响,后文测点位置均为2 mm。

图8 混合率测量位置对混合率数值的影响Fig.8 Influence of measuring position on mixing index curve

当矩形格宽度为0.167 mm时,研究矩形格长度对混合率计算的影响。固定矩形单元格左边界,选取长度依次为0.16、0.2、0.24、0.28、0.32 mm共5组数据进行数值计算,结果如图9所示。

图9 混合率测点矩形格长度对混合率数值的影响Fig.9 Influence of measuring cells’ length on mixing index curve

随着矩形格长度的增加,整体曲线向右上方略微移动,即混合率增加、相位后移,但增加的幅度相对较小,说明矩形格长度对混合率定量描述影响较小,因此后文均取矩形格长度为0.16 mm。

同理,保持测点位置为2 mm以及矩形格长度为0.16 mm,研究矩形格宽度的影响。在矩形格需覆盖出口通道截面的前提下,其宽度等同于通道宽度方向矩形格的数目。矩形格数的增加会使混合率计算值呈现较大变化。本文在一个周期内选取4个时间点,针对每一个时间点研究多组矩形格数对混合率的影响。

如图10所示,当矩形格数为1时(对应宽度为1 mm),测点位置处仅有一个横跨整个出口通道宽度方向的矩形格(管道直径为1 mm),局部混合率主要依靠交界线粒子法测量,计算得出的数值偏高,且随着矩形格数的增加(宽度的减小)呈现较大非线性变化,如图中波动区域所示。当矩形格数进一步增加时,平均作用逐渐体现,使得整体混合率测量值趋于稳定,如图中平稳区域所示。当矩形格数在5～7(宽度为0.2～0.143 mm)时,混合率测量值随宽度呈线性变化,认为矩形格宽度变化对混合率计算的影响较小。因此,本文取测量矩形格数为6,对应宽度为0.167 mm。

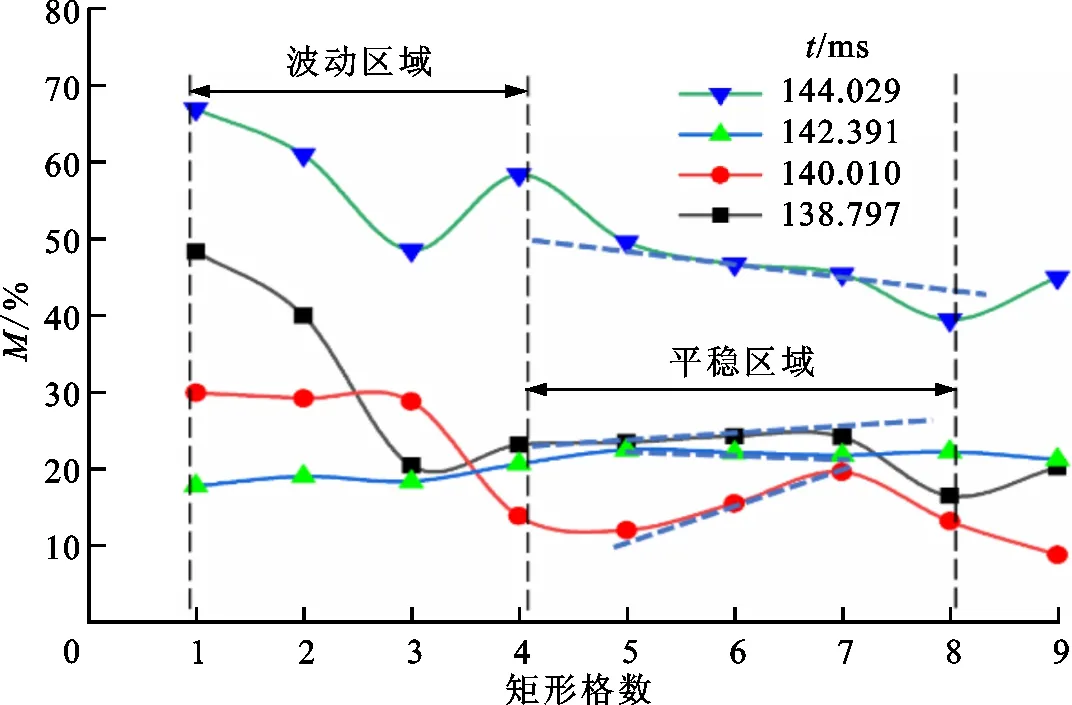
图10 混合率测点矩形格宽度对混合率数值的影响 Fig.10 Influence of measuring cells’ width on mixing index curve

3.2 Y型进口微混合器内流动机理分析

3.2.1 两不互溶液体混合机理 仿真参数选自文献[13],二次流主要产生于叶尖与混合室上半部分内壁的间隙处,如图11所示,混合主要由叶片顶端与混合室内壁之间的间隙产生的二次流驱动。当叶片逆时针旋转时,混合室上半部分的叶片与上层进口通道流入的液体逆向运动,在混合室上半部分构成了逆流区,加强了间隙处的剪切流动。

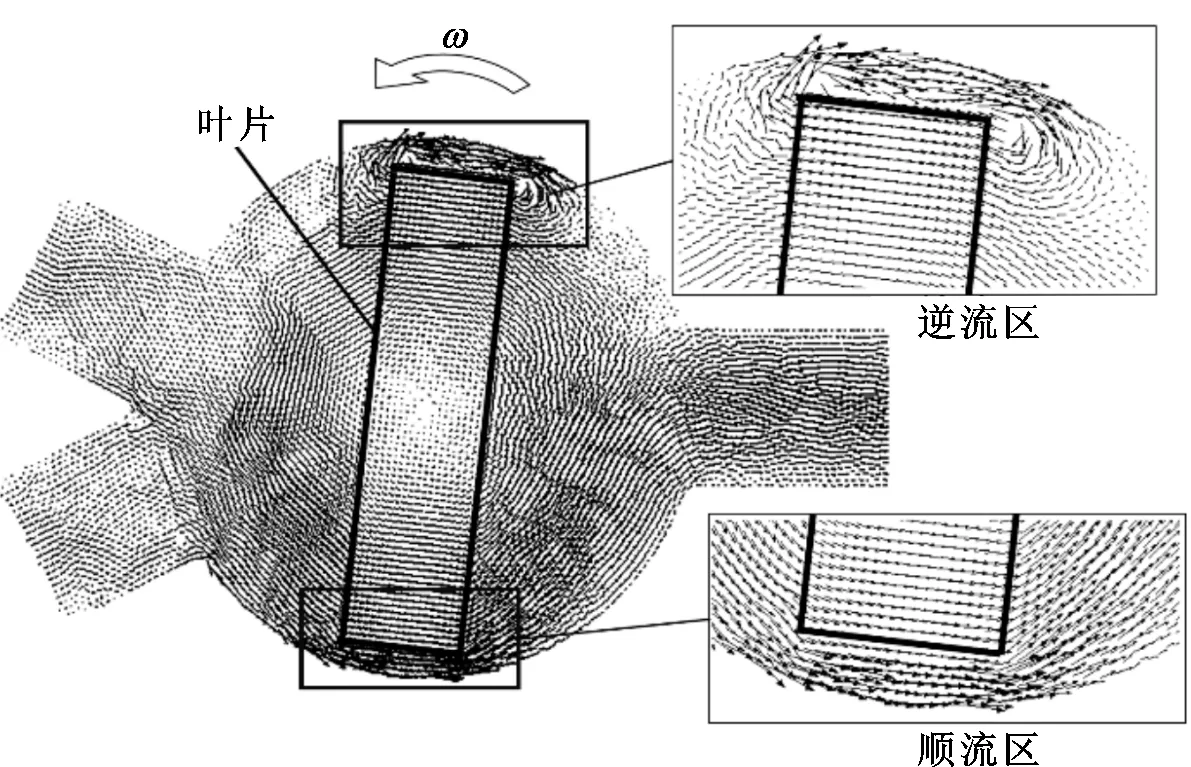
图11 混合器内速度矢量箭头图Fig.11 Diagram of velocity vector in the chamber

叶片压力面与吸力面的压差使得液体在叶顶间隙处出现反向流动,如图12所示。叶片吸力面尤其是叶顶处,由于叶片旋转和液体回填产生了跟随流动。该流动与上述间隙回流汇合,在叶片吸力面端部产生了持续的漩涡。该漩涡进一步促进了两种液体的掺混。

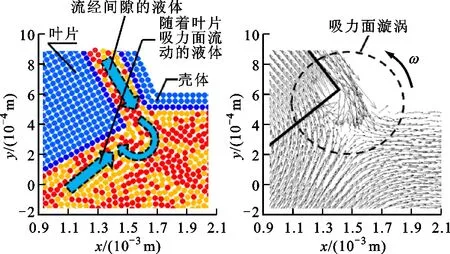
(a)t时刻粒子分布图 (b)t=0.04T时刻流线图图12 吸力面漩涡产生机理Fig.12 Producing mechanism of vortex on suction surface

在混合室下半部分,叶片与下层进口通道的流体同向运动,在该部分构成了顺流区,叶片主要起输运作用,剪切作用较小,混合效果相对较弱。

混合室内部流动过程可分为混合与输运。混合主要发生在混合室逆流区,输运主要发生在混合室顺流区。混合与输运交替发生,最终导致出口流体的混合率也呈现周期性波动,如图13所示。

图13 出口通道2 mm处局部截面混合率随时间的波动Fig.13 Change of local mixing index with time at 2 mm of the outlet channel

在一个周期内,以t=420 ms为起始时刻(见图14a),研究一个稳态周期内混合器的内流情况,选取6个典型时刻,如图14a～14f所示,红色、黄色分别代表两种不互溶液体,混合室内的流动混合整体呈现周期错位的混合-输运特性。

当t=420 ms时,混合室上部存在两种流体,上一周期已混合流体团Ⅱ与这一周期准备混合的流体团Ⅰ。随着叶片旋转,流体团Ⅰ经由间隙与邻近不相溶液体混合为流体团Ⅲ(见图14b),大部分流体团Ⅲ已充分混合并置于叶片后端,但由于剪切作用的局限性,仍有一小部分流体团Ⅲ以未混合的状态滞留在叶片前端;已混合的流体团Ⅱ除后端极小部分也参与间隙混合外,大部分经由叶片的推动以及上层进口流体剪切的双重作用,于叶片左侧形成长条状混合流体团Ⅳ。

当叶片尖端转过上层流入通道时(见图14c),持续流入的上层流体将流体团Ⅲ彻底分离,并阻碍这个周期已经混合好的流体团Ⅴ进入混合室下部,由此形成了周期错位的混合-输运模式。

随着叶片继续旋转(见图14d),逆流区液体准备进入下一个周期的混合,顺流区液体进入输运流程。此时,顺流区内的流体呈现分层排布。从壁面到叶片依次为下层通道流入的未混合流体团Ⅵ、上层通道流入的未混合流体团Ⅶ、充分混合流体团Ⅷ。由于壁面黏性作用,受到的黏滞阻力最大的流体团Ⅵ最后流出通道,流体团Ⅷ受到的黏滞阻力最小,最先流出通道。

此外,流体团Ⅵ、Ⅶ、Ⅷ均有一部分留在混合室内,继续参加下一周期混合。如图14e所示,对于充分混合的流体团Ⅷ,在离心力、惯性力以及直管道与混合室连接处尖角的共同作用下,仅有部分流出。流体团Ⅵ、Ⅶ也经历该过程(见图14f)。此后,混合器内流体回归周期起始状态。流入出口通道的流体团由于通道壁面黏性力的作用,逐渐形成V字形,如图15所示,且以流体团Ⅵ、Ⅶ、Ⅷ的次序交替循环,这便导致了测量的混合率呈现低-低-高的周期性波动,如图13所示。

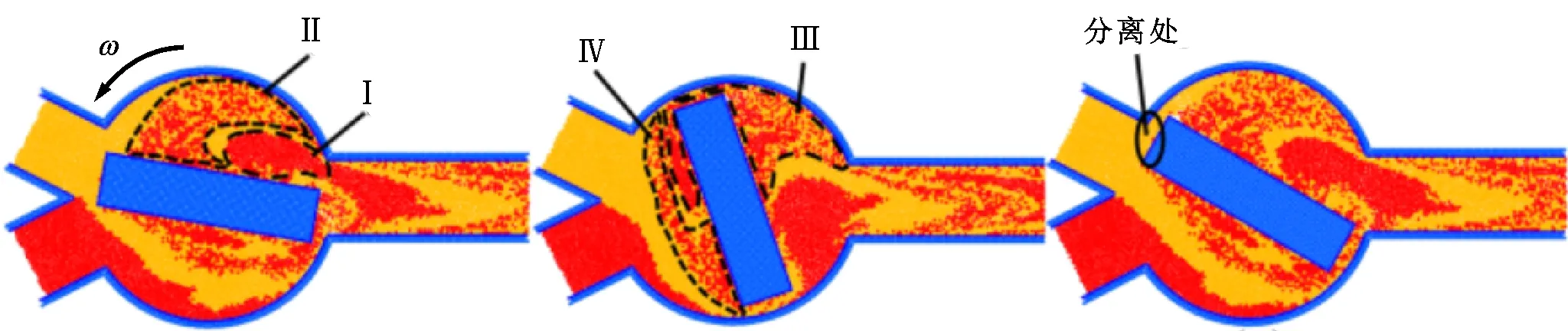
(a)t=0 (b)t=0.36T (c)t=0.46T

(a)流体团Ⅷ (b)流体团Ⅶ (c)流体团Ⅵ图15 出口管道流体的周期性Fig.15 Periodic characteristic of outflow fluids

3.2.2 流量与转速对混合率的影响 由前述机理分析可知,混合程度的恶化主要由图14e中来自上、下层通道的未混合流体团Ⅵ、Ⅶ导致,本节定义图14e中流体团Ⅵ为低混区,研究进口流速、叶片转速对该低混区的影响。取叶片转速为2 200 r/min,选取0.1、0.08、0.06、0.04、0.02 m/s共5组进口流速数据进行计算。计算进入稳态后,取同一叶片相位,观察此时低混区的分布,计算结果如图16a～16d所示。进口流速为0.02 m/s时,混合室顺流区的液体分布基本均匀。

相关文献研究均表明,转速升高在一定范围内可以提高混合程度,但过高的转速反而会使混合率下降[1,3-5,13]。本文保持进口流速为0.119 m/s,从1 400 r/min起,间隔200 r/min取8组数据进行数值计算,部分结果如图16e～16h所示。

当叶片刚掠过下层进口通道时,下层进口通道的液体在上层通道流入的液体以及惯性力的作用下,流向叶片与混合室下部间隙,该部分未混合流体流速急剧加快,体积减小,但在通过间隙后,速度锐减,体积增大,由此在叶片前端形成较大的未混合流体团,也即低混区。

叶片转速固定时,进口流速越小,单位时间内下层流体通过间隙的流体体积越小,因此低混区的体积逐渐减小(图16a～16d),混合程度提升。当进口速度固定时,低混区的体积会随着叶片转速的增大而减小(图16e～16h)。这是由于随着转速增加,单位时间内叶片转过更大的角位移,导致叶片与混合室内壁之间的间隙同样沿旋转方向移动更大的距离。进口流速一定时,相当于间隙内的过流液体的速度降低,因此单位时间内通过该间隙的液体体积相对减小,也即形成的低混区体积减小。

(a)进口流速0.10 m/s (b)进口流速0.08 m/s

(c)进口流速0.06 m/s (d)进口流速0.04 m/s

(e)叶片转速2 800 r/min (f)叶片转速2 400 r/min

(g)叶片转速2 000 r/min (h)叶片转速1 600 r/min图16 进口流速与叶片转速对低混区的影响Fig.16 Influences of inlet velocity and rotating speed on poor mixing regions

综上,低混区的产生与进口流速以及叶片转速的相对大小有较大关系。当进口流速相对于叶片转速占主导地位时,混合室下部的叶片前端容易出现较大体积的“被挤压”状低混合区域。

提取一个稳态周期内不同进口流速、叶片转速对应M-t曲线平均值的变化,如图17所示。在本文研究的转速范围内,进口流速固定时,平均混合率随着叶片转速的提高而升高。叶片转速一定时,减小进口流速,在一定范围内可以减小低混区的体积,优化混合器内混合程度。但是,过小的进口流速(小于0.2 m/s)会阻碍逆流区二次流的形成,大幅度降低混合率。此外,过低的进口流速也会导致该混合器效率的下降。

图17 混合率随进口流速以及转速的变化 Fig.17 Change of mixing index with inlet velocity and rotating speed

4 结 论

本文利用无网格粒子法在计算大变形、捕捉动态混合交界面方面的优势,建立了充分发展速度进口模型,结合移动边界模型,数值模拟了Y型双进口单叶片微混合器内两种不互溶液体的混合过程,揭示了其内部流动及混合机理,研究了进口流速与叶片转速对混合率的影响。基于粒子法拉格朗日特性,提出了一种可描述局部理想有序混合的混合率计算方法,研究了相关参数对混合率计算的影响。

研究结果表明,叶片旋转与混合器壁面形成顺流区和逆流区。叶片吸力面补流与叶顶间隙逆流交汇产生的尾迹漩涡,是促进搅拌混合的重要因素。转子转动产生的周期性混合-输运特性,使得出口管道混合率随时间呈周期性波动。低混区的大小受进口流速与转速的共同影响,在本文研究的范围内,适当提高转速或降低进口流速都可缩小低混区并提升混合率。转速与进口流速匹配,可获得局部最优混合率,相关规律将在后续研究中进行报道。本文揭示的流动机理及数值分析结果,可为提升微混合器混合率及其优化设计提供指导性建议。