基于轨排特征的中低速磁浮轨道检测里程校正方法

李中秀 吴峻 张云洲 谢云德

（1.北京轨道交通技术装备集团有限公司磁浮研究院长沙分院，长沙 410073；2.国防科技大学智能科学学院，长沙 410073）

随着中低速磁浮轨道交通的发展，关于磁浮轨道检测系统（包括静态轨检仪和搭载式动态检测系统）的研究也已展开。通过检查磁浮轨道的几何参数，及时发现轨道病害，保障车辆运行的稳定性、安全性及乘坐舒适性［1]。轨道检测系统的里程是采样和对比轨道检测数据的基础。测速定位系统输出列车的速度和位置信号，为列车运行控制系统正常工作提供必要信息，是列车的关键部件。搭载式轨道检测系统的里程信号来自列车的测速定位系统，因此中低速磁浮列车的测速定位精度受列车运行加速度的影响。静态轨检仪的里程信号来自走行轮编码器，其精度受走行轮直径磨损变化的影响，可能导致无法准确查找轨道病害。因此，须对绝对里程的起始点和相对里程等实施校正［2-3]。

在轮轨交通的轨道检测领域，文献［4]提出了GPS（Global Positioning System）里程自动校正方式，但是GPS 接收器受环境影响较大，高楼大厦附近可能无法工作，设备复杂，校正误差在10 m 左右。文献［5]使用射频识别技术（Radio Frequency Identification，RFID），绝对里程的定位精度可达为0.2 ～0.6 m，但须额外铺设大量地面设备，造价过高。文献［6]提出基于函数极值点快速提取的五点迭代法用于里程校正，可实现里程修正误差在3 m以内，但计算复杂。

与轮轨交通的轨道不同，中低速磁浮轨道为高架分段铺设，考虑到受热胀冷缩的影响，轨排之间都留有0 ～40 mm 的缝隙，即轨缝（图1）。同时，为了适应不同的圆曲线及竖曲线，部分轨排也被设计成特定的长度［7]。利用轨缝以及部分特定轨排长度的确定性和排列组合，本文提出一种简便有效的磁浮轨道检测里程校正方法，将检测结果与线路设计的各轨排长度进行匹配，确定检测数据的里程起始点，并校正每段轨排的里程检测数据。

图1 轨缝

1 里程校正方法

轨道检测的数据采集模式为空间采样，即沿里程方向等间隔采样。采样间隔d取0.024 m。轨道检测数据中，用于测量垂向位移的激光位移传感器在轨缝处的输出值会发生突变［1]。通过对垂向位移进行突变判断求出相邻轨缝之间的采样点数P，可得其所对应的轨排长度为Pd。依此方法求出一次实测的轨排长度数组K，其中第i个轨排的长度为K［i]，0 ≤i≤m-1，m为本次数据的轨排数量。

从线路里程标起点开始，使用轨道检测设备对全线运行一次，并记录每段轨排的长度，结合综合铺轨图进行修正，得到后续校正的执行目标的长度L［i]，0 ≤i≤n-1，n为本条线路的全部轨排数量。以唐山1.47 km 中低速磁浮试验线（简称唐山试验线）为例，其轨排长度排列柱状图见图2。

图2 唐山试验线轨排长度排列柱状图

1.1 里程起始点定位方法

线路轨排长度数组L长为n（即L［0，…，n-1]），实测轨排长度数组K长为m（即K［0，…，m-1]），n≤m。有效位移s是K在L中第一次匹配成功的位置。以有效位移s=3为例，里程起始点定位方法如图3所示。

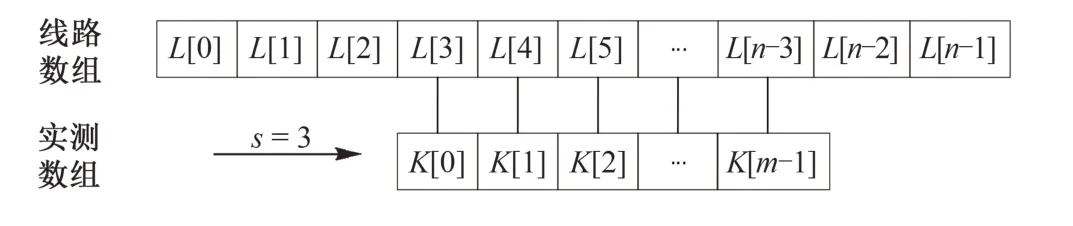
图3 里程起始点定位方法

在一次运行过程中共采集数据的长度为m，如果对于任意0 ≤i≤m-1 式（1）均成立，则认为在有效位移s处运行数据的起始里程定位成功。

式中：σ是轨排匹配阈值，在搭载式动态轨道检测系统中依赖于测速定位单元输出脉冲的精度，取0.02。

该次运行数据的起始点里程S0为

式中：j为第一个轨缝在检测数据中的索引位置。

1.2 轨排匹配算法的优化及使用条件

当磁浮线路的长度增加时，轨排匹配的计算量也随之增加。为了更快速地进行匹配，须寻求更优的匹配算法。在字符串匹配领域，有多种匹配算法，如Naive 算法、KMP（Knuth-Morris-Pratt）算法、BM（Boyer Moore）算法等。轨排匹配算法可以使用式（1）的匹配条件来代入字符串的匹配算法。在Naive 算法中，对线路数组L和实测数组K均未做预处理。发现K的元素与L的元素不匹配时，须将L的比较位置向后滑动一位，K的比较位置归0，并从头开始比较。在KMP 算法和BM 算法中，对K进行了预处理操作，预先计算了K中各位置的最长相同前后缀长度的数组。各算法的时间复杂度对比见表1［8-9]。

表1 各匹配算法时间复杂度对比

减小实测轨排数组的长度，是减少匹配运算量的另一个重要手段，但前提是减少长度后轨排数组的特征量不能改变，即在线路上只能成功匹配一次［9]。因此，须在线路轨排长度数组L中明确最小的数组子集，使其在L中仅能匹配成功一次。使用轨排长度相同的匹配算法在L中搜索最小数组子集的长度Lmin，搜索算法流程如图4所示。其中，a，b，c为搜索时所用的循环变量，每次搜索执行后加1，直到满足搜索条件为止。

图4 轨排数组最小子集的搜索流程

因此，当实测轨排数组的长度大于Lmin时，才能在L上匹配出唯一结果。唐山试验线共145段轨排，使用该搜索方式求得最小子集的轨排数量为43，合里程长度为390 m，即大于390 m的轨道检测数据才能使用轨排匹配算法仅匹配成功一次。

1.3 轨缝漏检问题的处理

轨缝宽度会随气温变化而变化。在温差荷载作用下导轨竖向变形，呈上拱抛物线形，最大上挠量为5.1 mm，跨中和梁端轨缝伸缩量为-4.7 ～0.3 mm［10]；考虑到铺设过程中轨缝宽度大小不一，当轨缝宽度小于采样间隔d时，则可能出现轨缝漏检的问题。此时，K［i]实际上是线路轨排数组中相邻若干元素的和。在应用式（1）求匹配阈值前，须先判断当前检测轨排对应的实际轨排数量。判别公式为

式中：H(i，j)为第s次比较时从i开始连续j个标准轨排的和减去K［i]得到的差的绝对值；T为最大连续漏检轨缝数量。

根据唐山试验线的检测数据，其轨缝最大连续漏检数量小于10。因此，此处取T= 10。假设H（i）在j=t时取值最小，则式（1）的匹配条件可表示为

1.4 里程校正功能的实现

起始里程的轨排匹配功能实现后，轨排内相对里程校正的实现就比较简单了。对于有效位移s，0 ≤i≤m，如果K[i]＜L[s+i]，则在第i个轨排长度K[i]对应的K[i]/d个检测数据中均匀插入(K[i]-L[s+i])/d个数据，使插入点的数值与前一个采样点的数值相等。如果K[i]＞L[s+i]，则执行对应的均匀删除操作；如果K[i]=L[s+i]，则不做处理。

2 里程定位和校正的精度分析及验证

为了量化匹配误差，定义ε为一次匹配行为的平均误差，表达式为式中：N为本次测量检测到的轨排数量。

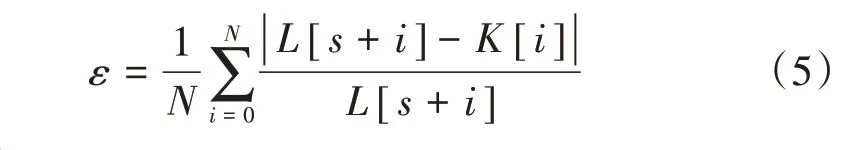
若考虑轨缝漏检，由式（3）确定最小H(i，j)后，式（5）中的L[s+i]由代替。

搭载式动态轨道检测系统在唐山试验线上运行6次，分别计算其匹配误差，结果见表2。可知，运行速度较快时加速度变化也大，其匹配误差普遍偏大。

表2 唐山试验线匹配误差

根据中低速磁浮轨道的特性，若其不平顺、高低曲率等指标超标，则调节轨枕上的螺栓高度。轨枕的平均间距是1.2 m，故里程校正的精度在1.2 m 内即可［11]。采样基于轨排特征的校正技术，里程的总误差取决于脉冲累加的误差和测速定位单元的误差两个方面。相对里程校正解决了脉冲累加的误差，而测速定位单元在最大轨排长度内。通过平均匹配误差来评估脉冲累计误差，其误差小于1.2 m。

轨距是轨道几何参数中最稳定的参数，且其测量受列车运行状态影响小。为了验证里程校正效果，轨距-里程波形对比是比较理想的选择。唐山试验线轨距曲线校正前后的轨距-里程波形对比见图5。可知：里程校正前检测数据重合度较低，校正后重合度明显提高；里程校正后重复性误差小于1.2 m。

图5 唐山试验线校正前后轨距-里程波形对比

3 结语

本文提出的基于轨排特征的磁浮轨道检测里程定位及校正方法仅使用轨道检测装置中所使用的激光位移计以及轨排长度的确定性和排列组合，就能够完成轨道检测数据的里程定位及校正功能。该方法降低了轨道检测系统设计的复杂性，使得轨道检测数据里程误差能够控制在1.2 m 范围内，具有很高的工程应用与推广价值。