高中数学美学认知三境界的探讨

谢锦辉

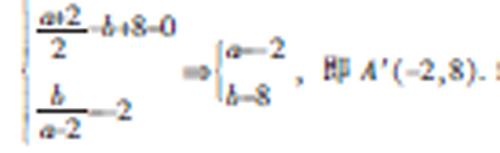
数学教育家张奠宙先生从数学教育者的角度就数学教学过程中如何展现数学美提出了四个层次：美观、美好、美妙、完美，并对每个层次做详细阐述. 本文从数学初学者角度和数学文化角度，提出初学者感悟数学美学的三种境界.

对称性是最能给人以美感的一种形式，德国数学家和物理学家魏尔曾指出：“美和对称性紧密相关.”对称美反映了事物的秩序、简洁、完整以及彼此的联系，显示了运动的稳定性和对立的统一性，反映了审美对象和结构的平衡，体现了平衡之美.

第一境界：以形感之——以数学形态让学生直观感受数学美

第一境界与张奠宙先生的数学美第一层美观是一致的. 这主要是指数学对象以形态上的对称、和谐、简洁，给人带来感官上美丽、漂亮的感受. 从数学形态美入手，让学生感受数学形态之美，可以让学生对貌似繁杂的数学产生兴趣，萌生学好数学的念头.

在对称美的教育中，我们可以通过对比，让学生直观感受“对称”带来的美;我们可以从自然形态中抽象出数学图形，让学生感受数学直观形态之美，体现数学与自然的完美结合.

例1：美与不美——有对比才有说服力.

图形是非常直观的一种形式. 显然，在上述三图中，左右两边的图具有对称性，中间的图给人一种怪怪的感觉，相对于中间图形，左右两边的图形会让欣赏者更加心情愉悦.

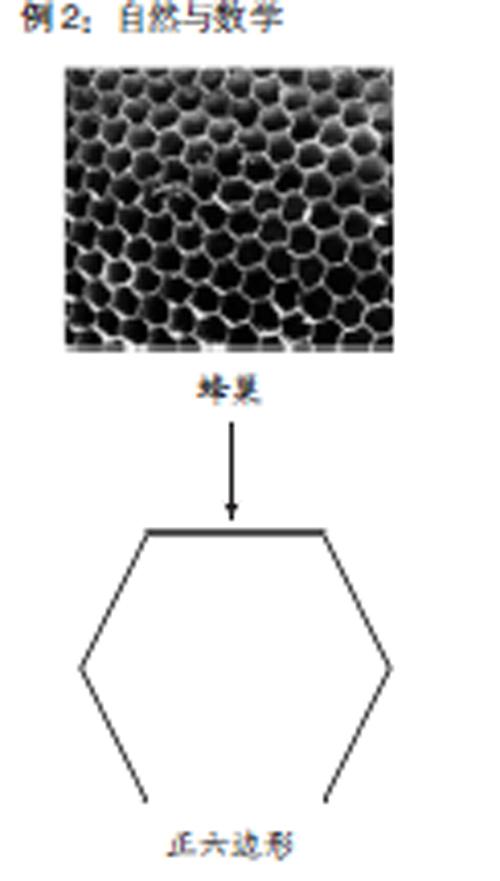
例2：自然与数学

蜜蜂选择正六边形蜂巢不仅因为正六边形对称、漂亮，还有其他更深刻的原因，但这种自然的选择体现出数学对称美与自然的和谐统一.

第二境界：以理服之——让学生理性认知数学美

如果我们仅仅停留在对图形美的思考，学生既无法深入提升美学素养，也无法深入理解数学美学. 因此我们需要思考“美从何来？”“美本质在何处”，即穷美之理，以理服之.

在以理服人的过程中，我们既可以结合生活實际，也可以与经验常识结合，使学生在纵横捭阖之间，打破数学学习的封闭性，不再囿于于数学本身，在数学原理、数学知识运用、数学手段掌握上能够更接地气，有利于学生内化数学知识、活用数学.

在对称美的欣赏中，我们至少可以从两个角度进行赏析.

第一角度：对称美的产生来源于内心的满足. 从美学角度，美是人对自身需求被满足时所产生的愉悦反应. 由对称的性质，我们可以对具有对称结构的事物“窥部分而得整体”，达到“一叶知秋”的效果;利用镜面对称也能达到“知一得二”的效果. 这两种效果都可以使我们利用“较少的已知信息”获取“较多的未知信息”，既能够满足“以小博大”“事半功倍”的人性，也可以使人减少对未知的恐惧，从而产生内心的愉悦，美由此产生.

例3：利用对称结构进行条件转化.

已知直线l ∶ x-2y+8=0和点A（2，0）、点B（-2，-4），在直线上求一点P，使 |PA|+|PB|最小，则P点坐标是_______.

分析：|PA|+|PB|≥|AB|，等号成立条件为A、B在P的两侧，显然原题不满足等号的条件. 若要满足等号的条件，A、B两点必须在直线的异侧. 为此我们可以利用对称性质，将点A转化到直线另一侧，然后利用两点之间线段最短的定理得到最小值.

解：设点A（2，0）关于直线x-2y+8=0对称的点坐标为A′（a，b），则-b+8=0=-2  a=-2b=8，即A′（-2，8）. 结合图形可知|PA|+|PB|≥|AB|，即三点A′、B、P共线时，|PA|+|PB|最小，此时直线A′B的方程为 x=-2，将x=-2代入直线x-2y+8=0可得交点P（-2，3）.

第二个角度：对称美体现了事物平衡. 对称是指事物整体中各个部分之间的匀称和对等，而匀称又往往与和谐的协调性相联系. 这种协调即是平衡. 平衡观的引入，为数学解题提供了思路，为数学学习赋予了生活气息，也为数学学习赋予了哲学意义.

例4：从平衡角度思考问题的解决.

我们在推导椭圆方程过程中，多次利用了对称美和平衡的思想.

（1）对称建系

很明显在上述三图中，中间的建系很漂亮，左右平衡、稳定美观. 这种对称建系给后续的化简带来美的体验，为最终结果的简洁性提供保障.

（2）从平衡角度化简代数式

根据椭圆的定义，设M（x，y）是椭圆上任意一点，椭圆的焦距为2c（c>0），那么焦点F1、F2的坐标分别为（-c，0）、（c，0）. 根据椭圆的定义，设点M与焦点F1、F2的距离的和等于2a.

由椭圆定义可知，椭圆可以看作点集P={M│|MF1|+|MF2|=2a}. 所以有：

这一步的变换思路的来源即是满足等式的平衡. 从代数式整体结构来看，变换后等式两边结构更加均衡、稳定. 这种均衡为后续化简提供了便利.

例5：从平衡角度思考等价转化.

证明：对一切x∈（0，+∞），都有lnx>■-■成立.

分析：本题从代数式结构来看，不等号左右两边的结构是不平衡的. 左边lnx是初等函数，形式简单;右边为指数函数和反比例函数的和函数，研究起来非常繁杂，即便求导后导数也很复杂. 从不等式结构均衡的角度，我们将不等号两边同时乘以x，将问题转化为证明xlnx>■-■，x∈（0，+∞），这样，左边代数式结构变复杂，但右边代数式结构变简单，不等式结构相对均衡，然后通过分别研究不等式两边的函数，得到不等式的证明.

证明：易知f（x）=xlnx的最小值 f（■）=-■. 设 （x）=■-■，（x∈（0， +∞）），则？覬′（x）=■;由？覬（x）的单调性易得 ？覬（x）max=？覬（1）=-■，因此xlnx≥-■≥■-■，因为两个等号不能同时取得，所以xlnx>■-■，即对一切x∈（0，+∞），都有lnx>■-■成立.

第三境界：以用喜之——利用对称美解决实际问题

以理服之，能够让学生深刻感受数学美学. 但如果不能用美学之理指引我们解决问题，于学生而言就止步于数学之门，停留在欣赏美学，不能产生数学的美学体验. 因此教师需要利用数学美学解决学生遇到的数学问题，让审美意识产生实际效用，使学生感受“美学之用”. 让内化的美学之理外显，指导学生解决问题，既丰富数学美学体验，也能感受数学之用.

由前文所述，可以看到对称美的产生来源于可以用“较小的代价”获取“最多的信息”，因此利用对称美可以达到“化繁为简”的效果.

例6：已知A、B分别为椭圆E：■+y2=1的左、右顶点，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D.证明：直线CD过定点.

分析：本題解法很多，但是大都涉及到直线与椭圆联立方程、求点等，计算繁杂. 如果我们能够关注到C、D点的对称性，利用对称美学可以得到一个非常漂亮的解法.

解：由椭圆的性质可知：kAC·kBC= -■;kAD·kBD =-■;∴■=■;因为P是直线x=6上的动点，由几何性质可知：kAC=kPA=■;kBD=kPB=■;∴3kAC=kBD，∴■=■=■;设直线CD方程为x=sy+t，由上述可知：3kAC=kBD且3kAD=kBC

∵3kAC=kBDxC=syC+txD=syD+t  3■=■xC=syC+txD=syD+t

2syC yD+（3t-9）yC-（t+3）yD=0……①

同理：3kAD=kBC？圯2syCyD+（3t-9）yD-（t+3）yC=0……②

则①-②得：（9-3t）（yD-yC）=（t+3）·（yD-yC）……③

∵yC≠yD，由③可知，t=■. 所以直线CD的方程为x=sy+■，因此直线CD恒过点（■，0）.

将数学美学教学引入高中课堂，可从直观感知、理性认知、学以致用三个逐层递进的境界认知数学美学. 在这个过程中学生能够打破数学学习封闭性，提升数学学习兴趣、内化数学素养、增强学习内驱力. 更重要的是，以数学美学角度注入课堂教学，可以丰富学生情感体验、提升学生美学修养、提高学生核心素养. 这也是数学学习的价值和意义之所在.

注：本文系广东省教育科学“十三五”规划课题“普通中学生态美育体系的研究与实践”（课题批准号：2020ZQ JK071）阶段性成果.

责任编辑罗峰