“深备”的实践与思考

周雯

摘要：深度备课作为课堂教学的第一环节，是提高数学教学效果的重要途径。本文结合具体教学案例，从学生原有数学认知上的适度提升、学生思维生长点的精准把握、知识逻辑结构的重新梳理、知识学习实用性与必要性的感受、数学知识内在文化的历史溯源等方面探索如何有效开展深度备课。

关键词：本真心 深备 备學生 备知识内容

裴光亚先生曾说：“教育价值是教学设计的灵魂。”深备，顾名思义，就是深度备课。深备，需要备学生的认知、学情、年龄特点、常有的思维特点等，做好充分的预设;深备，需要备教材内容，如这一知识的历史史源是什么，前后位知识是什么，与前后位知识的逻辑关系如何？下面笔者就在深备中的几点做法与同人们交流一下，请斧正。

一、“深备”——学生原有数学认知上的适度提升

《义务教育数学课程标准》指出：数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。如果初中教学内容只是小学内容的再现，那就是“浅备”，这样的课堂一定是低效、无趣、无挑战的。教师要把学生小学时对知识的直观感受提升到理性认识层面上来，为此要进行“深备”。

案例1：《一元一次方程及其解法》

此课是沪科版七年级上册第三章第一节第一课时的内容，教学目标是通过两个实际问题情境，体会列方程解决问题的必要性和简便性，体会方程是刻画现实世界的一个有效数学模型。学生在小学阶段已经学习过等式基本性质1、2，也会熟练运用等式基本性质解方程，如果花费过多时间再次学习等式基本性质，课堂节奏将不会流畅。而且初中又增加了对称性、传递性等内容。基于此，教学设计如下：学习完一元一次方程概念之后，让学生求解一个一元一次方程。有了小学的认知基础，大部分学生能成功求解。重点是引导学生从数理角度分析每一步的依据，升华理论知识，再通过巧妙的设计让学生体会对称性的实用性，让等式基本性质的运用有抓手。深备，在原有认知上适度提升，找准小初衔接点，找准所学知识的前位知识，让课堂本真、高效。

二、“深备”——学生思维生长点的精准把握

教师如同医生，有经验的医生能把病人的病根找到，有经验的教师能将学生脑中模糊的、错误的认识找到，尽管不能“药到病除”，但这样的数学课更有数学味。让学生的数学思维活跃起来，必须通过问题实现。

海莫斯说：“问题是数学的心脏。”设计什么样的问题？如何精心设计？怎么提问？何时提问？达到什么目的？这必须要找准学生的思维生长点，充分预设，让知识生成得自然。

案例2：《多边形的内角和》

这节课的前一部分内容是多边形的定义及相关概念，这里就可以让学生基于四边形的定义自己去给多边形下定义，这就是学生的思维生长点。学生会说：“由不在同一条直线上的若干条线段首尾顺次相接组成的封闭图形叫作多边形。”按照学生类比得出的结论，再次预设，基于学生思维，进行教学设计：准备好教具（4根细吸管，用线穿过吸管，刚好首尾依次相接），沿着对角线折起两条线段，是四边形吗？学生会意识到定义的漏洞，并强调是在平面内！于是得出多边形的定义。

进行如何求多边形的内角和教学设计时，也需要寻找学生的思维生长点，那就是求四边形ABCD的内角和。

学生最容易想到的办法是连接对角线AC或BD，将四边形的内角和转化成三角形的内角和。基于此，展示连接AC、BD连接后的图，追问：你能用其他方法证明吗？

根据学生的叙述用几何画板展示：

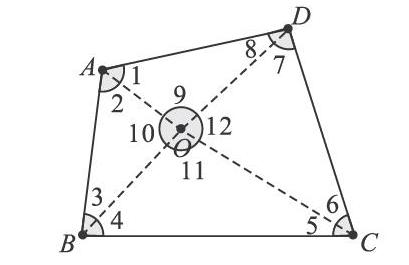
学生的回答就是学生的思维生长点。再提问：对角线的交点很特殊，如果这个点不是特殊点，它只是内部的任意一点，你能证明吗？于是得到图1。

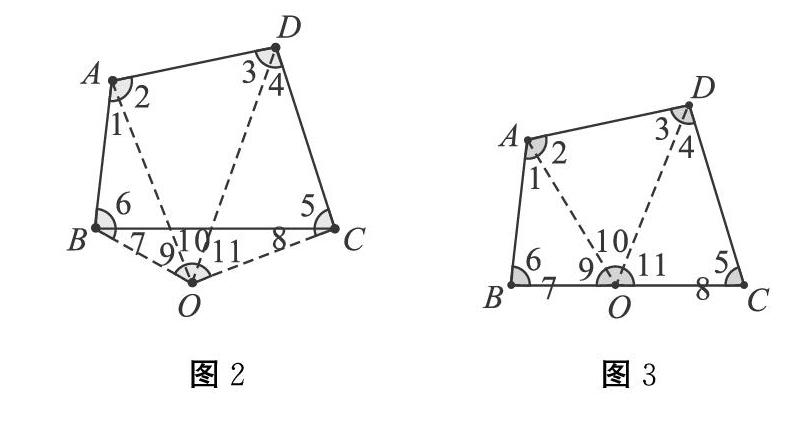
学生能感受到证明过程同理。进而提问：这个点O还能在哪呢？由点在外部或者在边上，得到图2、图3。

基于将四边形问题转化为三角形问题的这么多方法，再提问：你认为哪种方法最简便？再基于求四边形内角和的经验，继续求五边形、六边形、n边形的内角和。

最后，基于n边形内角和的多种求法，在观察总结中完成下表。

有的老师是为了填表而填表，一开始就呈现表格，一味要求把内容填上。其实填表只是为了帮助学生总结结论，表格只是工具，恰当地呈现表格需要老师找准学生的思维生长点。

三、“深备”——知识逻辑结构的重新梳理

知识的前因后果是什么，它的逻辑起点是什么？怎么设计更有逻辑性？整体架构是什么样？对于这些问题，教师要做到胸有成竹，统筹全局。

案例3：《线段的长短比较》

为什么线段可以进行长短比较？用比个子类比，到底比的是线段的什么？比线段比的是长度。正因为有长有短，所以两个量之间才可以进行比较。而大小关系有几种？三种。这三种关系又是如何体现在两条线段比较上的？体现在书写符号上，如AB>CD，指的是AB的线段长度大于CD。

中点知识为什么出现在《线段的长短比较》这一节呢？其实，该知识点仍然涉及线段长短比较。当线段AB上有一点C，必然有AC，BC这两条线段，当AC=BC时，C即为中点。因此，中点的逻辑起点仍是线段长短比较。

关于基本事实“两点之间线段最短”，从A到B有直的线，也有曲的线，这不正体现了直的线和曲的线的长短比较吗？这相当于线段长短比较的延伸。理解逻辑起点，构建正确的逻辑框架，有助于教学思路更清晰。

四、“深备”——知识学习的实用性与必要性

很多时候，课堂教学如果没有有效的抓手，将显得苍白枯燥。因此，让学生充分感受知识学习的实用性与必要性，是备课的主要内容。

案例4：《比例线段》

学生在小学阶段已经学过内外项积相等，由x∶y=3∶2得到2x=3y;反之，根据2x=3y，求x∶y等于多少时，大部分学生总会出错。

x：y等于多少？根据内项积等于外项积，应该等于3∶2。写3的时候，要明确告诉学生紧盯3y。那若ab=cd，得到哪些比例式呢？学生可能会很快写出ac=db，或者ad=cb，当追问“还有不同的比例式吗”，学生可能会感觉能写出很多情况，但又觉得写其他的比例式没什么用，都差不多。

老师可以画个典型图，让学生思考：若是要证明AB×CD=EF×GH，怎么证呢？告诉学生：先要学会将乘积式化成比例式，根据图形特点，将哪条线段放在第一项写，就决定了你后面三项怎么比。

讲解总要有个合理的载体，让学生觉得有必要学，体会到一节课所学的知识究竟怎么用。哪怕只是为了会解题，也要让学生在课堂上亲自解一解。

因要让计算更简便，需要学习运算律和总结公式;因生活出现了负数，不得不定义有理数;因存在无理数，不得不扩充到实数;因相等学习等式;因不等学习不等式;等等。这些都体现了知识学习的实用性与必要性。

五、“深备”——数学知识内在文化的历史溯源

数学教学不仅要教知识，还要关注知识内在文化的联系。知识教学其实也是文化教学，更多地了解历史发展故事对教学有很大的帮助。

案例5：《用字母表示数》

七年级上册第二章《用字母表示数》，是代数的基础、基石。要知道，从用文字来表示一个代数问题的解法，即修辞代数，到用字母表示未知数，即缩略代数，经历了2000多年。再从缩略代数到符号代数，即用字母表示任意数，又经历了1300年。我们在教学时，一节课时间就想让学生理解古数学家需要几千年才弄懂的知识，实在太不容易了。笔者在教学用字母表示数这一知识时，所带的两个班学生，只有很少一部分人能运用用字母表示未知数，他们想要真正理解用字母表示数、表示任意数，肯定是个缓慢的过程。

数学史是数学教师的重要教学资源。数学教师可以针对某个特定的知识点，融入相关的数学史，同时这也可以缓解教学压力。

深度备课，要备学生的学情、思维生长点，备知识的逻辑结构、学习必要性与历史文化。若只是“浅备”知识，终究只能是教书匠！