两组序列数据趋势变化特征对比分析的Joinpoint回归模型方法及应用
2021-05-08曾四清谢仕兰付笑冰龙其穗
曾四清 李 艳 刘 珺 谢仕兰 付笑冰 龙其穗 林 鹏
【提 要】 目的 介绍两组序列数据趋势变化特征对比分析的Joinpoint回归(JPR)模型的基本原理和方法,并以2006-2018年广东省HIV/AIDS病例数为实例进行分析。方法 该模型原理和方法主要来源于相关文献和应用软件,实例数据来源于国家艾滋病综合防治信息系统,采用Excel 2013建立数据文件,采用JRP软件进行分析。结果 2006-2018年广东省新发现的经注射毒品感染和经性传播的HIV/AIDS病例数分别拟合对数线性JPR模型的MSE为21.44和16.63,MAPE为9.51%和4.57%;二者的回归方程不平行(P<0.001)。其中,经注射毒品感染的HIV/AIDS病例数在2008年出现1个转折点,其前后分段的APC分别为12.64%和-17.75%,AAPC为-13.31%,呈先升后降和总体下降趋势;而经性传播的HIV/AIDS病例数在2008年和2015年各出现1个转折点,其前后分段APC分别为101.47%、22.26%和1.91%,AAPC为27.02%,呈持续上升趋势,但上升速度逐步下降,2015年后趋于平缓。两组的AAPC差异有统计学意义(z=-9.50,P=0.00),总体趋势变化方向及速度不一致。结论 该模型的应用拟合效果较好,两组数据拟合的回归方程及其趋势变化特征指标均存在显著统计学差异。研究表明,该模型适用于某些传染病序列数据趋势变化特征量化对比分析。
非参数趋势检验适用于计数资料,只能得出趋势结论,无法得到量化趋势指标,不同组别数据之间无法比较趋势变化大小;线性回归适用于计数资料和计量资料,有丰富的衍生模型,还可控制混杂因素,可计算趋势变化量化指标,不同组别数据之间可以比较趋势变化大小[1-4]。Joinpoint回归(joinpoint regression,JPR)是一种特殊的线性回归衍生模型,除了可以进行趋势变化参数估计量化分析外,还可以分析趋势变化的转折点,从而进行分段趋势变化特征分析;还可以进行两组序列数据趋势变化特征对比分析[5-6]。然而,目前有关该模型在传染病趋势分析中的应用研究文献较少。因此,本文介绍此模型的基本原理和方法,并以2006-2018年广东省HIV/AIDS病例数为实例进行分析,探讨其应用价值。
原理和方法
1.模型及计算原理
JPR模型分析的基本思想是通过模型拟合将一个长期趋势线分成若干有统计学意义的趋势区段,各段用连续的线性进行描述[5]。JPR模型分为线性数据模型和对数线性数据模型两类。假设有一序列观察值(x1,y1),…,(xn,yn),其中,yi(i=1,2,…,n)为因变量,xi(i=1,2,…,n)为自变量,x1≤…≤xn。线性数据模型表达式为:
E[yi|xi]=β0+β1xi+δ1(xi-τ1)++…+δk(xi-τk)+
(1)
对数线性数据模型表达式为:
E[yi|xi]=eβ0+β1xi+δ1(xi-τ1)++…+δk(xi-τk)+
(2)
式中,β0表示不变参数,β1表示斜率参数(回归系数);δk=βn+1-βn表示分段函数的回归系数;τk为未知转折点,k为转折点个数,当(xi-τk)>0时,(xi-τk)+=(xi-τk),否则,(xi-τk)+=0。
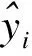
(3)
(4)
(1)两组序列数据的JPR方程(回归参数)比较[6-7]
假设(xij,yij)是i组序列观察值(i=1,2;j=1,2,…,n),yij为因变量,xij为自变量。假设xij=x,yij的回归方程为:
μi(x)=βi,0+βi,1x+δi,1(x-τi,1)++…+δi,ki(x-τi,ki)+
(5)
根据公式(1)和公式(2),对于线性数据模型,μi(x)=yi(x);对于对数线性数据模型,μi(x)=lnyi(x)。
检验1:比较两个回归方程是否一致(包括模型参数截距、转折点数、转折点位置和回归系数)。
设模型参数(ki,θi)=(ki,τi,1,…,τi,ki,βi,0,βi,1,δi,1,…,δi,ki)
无效假设H0:(k1,θ1)=(k2,θ2)
备选假设H1:(k1,θ1)≠(k2,θ2)
检验2:比较两个回归方程是否是不同截距的平行方程(包括模型参数转折点数、转折点位置和回归系数,但不包括截距)。
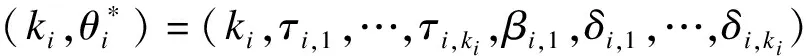

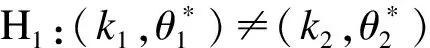
检验1和检验2的统计量计算公式为:
(6)
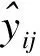
(2)两组序列数据JPR模型的APCi和AAPC比较[6,8]
APCi(annual percent change)是指序列数据的年度变化百分比,反映阶段性变化速度;AAPC是指序列数据全局或选定区段的年度变化百分比的加权平均值,反映平均变化速度。对数线性模型才可计算APC和AAPC并进行比较。
APCi及AAPC计算公式如下:
APCi={exp(βi)-1}×100
(7)
基于t分布假设计算APCi的100(1-α)%可信区间,公式为:
APCiL(α)=100{exp(βi-si*t-1di(1-α/2))-1}
(8)
APCiU(α)=100{exp(βi+si*t-1di(1-α/2))-1}
(9)
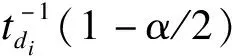
(10)
基于标准正态分布假设计算AAPC的100(1-α)%可信区间,公式为:
(11)
(12)
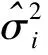
(13)
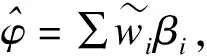
(14)
(15)
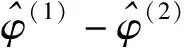
(16)
(17)
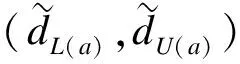
(18)
(19)
2.分析方法和步骤
采用Excel 2013建立序列数据的.CSV格式文件,采用JRP(Joinpoint regression program,JRP)软件4.6.0.0版[6]进行分析。采用网络搜索法(grid search method,GSM)分析转折点数量、位置及模型参数,采用Monte Carlo置换检验(permutation test,PT)和修正贝叶斯信息准则(modified Bayesian information criterion,MBIC)优选模型,选用其中MSE较小者的分析结果;采用置换检验方法进行两组模型回归方程比较,采用标准正态分布原理进行两组AAPC差异显著性检验。
分析时,在JRP 软件的“输入文件”(Input file)窗口设置模型参数,设HIV/AIDS病例数为因变量(dependent variable)、年度为自变量(independent variable)、感染途径为分组变量(By variable),模型类别选择为对数线性数据模型[ln(y)=xb];假设HIV/AIDS病例数服从Poisson分布,将异方差选项(Heteroscedastic errors option)设置为“Poisson variance”;在“方法和参数”(Method and parameters)窗口设置模型拟合方法为网格搜索法(Grid search)、置换检验(Permutation test),或者为修正贝叶斯信息准则(Modified BIC),经试分析本研究设最大转折点数(Number of joinpoints)kmax值为2,误差自相关选项(Autocorrelated errors options)设置为误差不相关模型(Fit an uncorrelated errors model),选用参数法(Parametric)计算AAPC;在“高级分析”(Advanced analysis tools)窗口,选择对比分析(Pairwise comparison)方法[6]。
3.应用条件和注意事项
(1)适用条件
经典线性回归模型基本适用条件包括:因变量y与自变量x呈线性关系;观察值相互独立;在一定范围内,任意给定x值,因变量y值都服从正态分布;不同x值所对应y值的方差相等。JPR模型是线性回归分析的一种衍生模型。对比分析JPR模型的因变量类型包括例数或“事件”数、发病率或死亡率、构成比、百分比,或其他数值变量等;自变量应是有序变量;同时,还应有分组变量,建立数据文件时需按分组变量排序。若因变量y不完全符合以上条件,则需对其进行数据转换(如对数转换)以达到适用条件,此时应采用对数线性模型[2]。当有因变量y值为“0”时,需用“0.5”替换后才能分析[6]。
(2)注意事项
对比分析JPR模型既可以是线性方程比较,也可以是对数线性方程比较,但如果要计算并比较APCi和AAPC,则应选择对数线性模型。
在JRP软件中,单一序列数据的JPR趋势分析既可选择非相关误差模型(模型中的随机误差具有方差齐同性或固定方差,其符合均值为0、方差为δ2的正态分布),也可选用自相关误差模型(即随机误差的方差随时间而变化);而进行两组对比分析时,只能采用非相关误差模型[6-7]。
进行置换检验时,需设定检验次数,取值范围为1000~10000。为了计算结果(P值)稳定,同时控制计算时间,一般设定至少为4499,JRP中的默认值为4499;还需设定最大转折点数kmax值,由于置换检验较耗时,且kmax过大反而降低检验效能,一般设定kmax≤4[7]。
通常AAPC不能代表APCi,但当分段数为0时,APCi即为AAPC。此时,AAPC的可信区间采用t分布修正,以保证其与APCi的可信区间一致[6];一般计算AAPC的区段是全局的,但其起始点或截止点也可以在全局范围内自行设定,应用灵活。
对比分析JPR模型能根据分组变量对多组序列数据进行两两比较分析,但不能同时进行3组及以上组的比较分析;在进行多组别之间的比较时,是否需要将相邻两组的序列数据进行合并分析,可根据两者比较的结果来判定。该对比分析方法不能用于只比较两组序列数据的转折点位置而不考虑其他回归参数的分析[7]。
实例分析
实例数据来源于国家艾滋病综合防治信息系统。2006-2018年广东省新发现经注射毒品感染与经性传播的HIV/AIDS病例数见表1,在此拟合对比分析JPR模型,进行两组病例数的年度趋势变化特征对比分析。
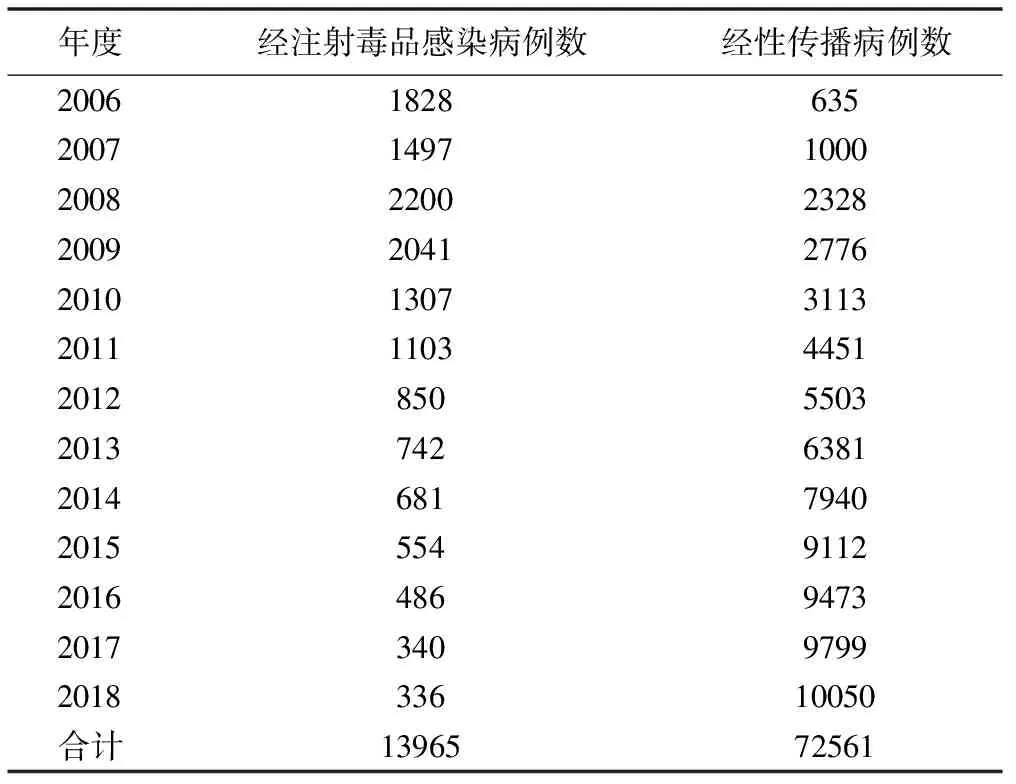
表1 2006-2018年广东省新发现经注射毒品感染与经性传播的HIV/AIDS病例数
1.两组病例数的年度趋势变化回归方程比较
2006-2018年新发现的经注射毒品感染和经性传播HIV/AIDS病例数拟合线性数据模型的MSE分别为47.37、25.63,拟合对数线性数据模型的MSE分别为21.44、16.63,均是后者小于前者,故采用对数模型进行对比JPR模型分析;置换检验、修正贝叶斯信息准则优选模型方程时,经注射毒品感染HIV/AIDS病例数拟合模型的MSE均为21.44,经性传播病例数拟合模型的MSE均为16.63,二者结果一致。两组的趋势变化特征比较见图1,有关参数分析结果比较见表2。经注射毒品感染的HIV/AIDS病例数回归方程为:E[yi|xi]=e-231.27+0.12xi-0.31(xi-2008)+,经性传播的HIV/AIDS病例数回归方程为:E[yi|xi]=e-1398.78+0.70xi-0.50(xi-2008)+-0.18(xi-2015)+。其中,xi为年度,取值为2006,2007,…,2018;E[yi|xi]为HIV/AIDS病例数。二者比较差异有统计学意义(P<0.001)。说明两组拟合的JPR回归方程不一致、不平行。

表2 2006-2018年广东省新发现经注射毒品感染与经性传播HIV/AIDS病例数回归方程参数
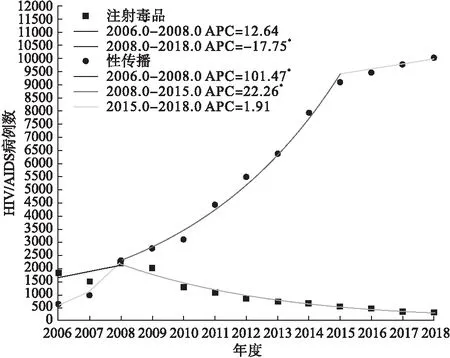
图1 2006-2018年广东省新发现经注射毒品感染与经性传播HIV/AIDS病例数趋势比较
2.APCi及AAPC比较
经注射毒品感染与经性传播的HIV/AIDS病例数拟合对比分析JPR模型的趋势区段、APCi及AAPC结果比较见表3。AAPC(1)-AAPC(2)=-40.30%(95%CI:-48.62%~-32.01%);z=-9.50,P<0.001。说明两组的AAPC差异有统计学意义,即两组的年平均变化速度差异有统计学意义。

表3 2006-2018年广东省经注射毒品感染与经性传播HIV/AIDS病例数趋势对比分析APCi(%)及AAPC(%)结果
讨 论
本文主要介绍了两组序列数据趋势变化特征对比分析的JPR模型的基本原理、计算方法、应用条件及注意事项。同时,以2006-2018年广东省新发现的经注射毒品感染与经性传播的HIV/AIDS病例数为实例进行了趋势对比分析。
JPR回归是分析某些疾病发病数或发病率序列数据趋势变化特征的实用方法[5,9-10]。JPR回归分析拟合的模型不一定最佳,但其优势在于能计算AAPC,反映整体的平均趋势变化方向和速度,也可应用于同一种类序列数据的不同组别之间进行趋势变化平均速度差异的量化比较,这是非参数趋势检验所不具备的功能[1-4]。而且,该模型能检测出有显著性意义的趋势变化转折点,并计算转折点前后各区段的趋势变化方向和速度APCi,从而揭示趋势变化转折点数量、位置和阶段性趋势变化指标特征[11]。同时APCi由于与AAPC一样,是一个无量纲的相对数,是反映趋势变化方向和速度的指标,因此,采用该模型进行时间序列发病数据趋势分析时,相同类别的不同病种之间、相同病种的不同时段之间或者不同组别人群之间等发病数据的APCi就可以进行比较分析。这些都是经典回归分析所不具备的分析功能[2]。正因如此,本文探讨了其在不同组别人群的传染病时间趋势对比分析中的应用。
两组的JPR模型拟合精确度均较高,两组的JPR回归方程比较差异有统计学意义,不一致、不平行。说明需要用不同的回归方程才能描述其各自的年度趋势变化特征。同时,两组的年平均变化方向和速度差异有统计学意义,说明二者的总体趋势变化也存在着差异,前者呈总体下降趋势,而后者呈总体上升趋势。其中,经注射毒品感染的HIV/AIDS病例数在2008年开始发生了显著性转折变化,从此前的上升趋势转变为此后的持续稳定下降趋势;提示广东省2005年开始开展的监管场所吸毒人群艾滋病筛查和2006年开始开展的社区戒毒药物维持治疗等防控措施取得了较好的成效。经性传播的HIV/AIDS病例数从2006年到2018年总体呈显著上升趋势,但在2008年和2015年开始出现了两次上升速度的统计学显著性变化,上升速度呈阶段性减低的特点,至2015年以后渐趋平稳,也反映了广东省采取的HIV/AIDS经性传播防控策略与措施产生了一定的积极效果。研究表明,该对比分析JPR模型适用于不同感染途径的HIV/AIDS病例数时间序列趋势变化特征比较研究,对比分析其趋势变化的转折点位置、方向和速度。参照上述方法,就可以对各种感染途径或者按其他因素分组的HIV/AIDS新发病例数、发病率或构成比等的趋势变化特征进行对比分析,以全面揭示其变化特征之规律及异同,进而对其背后的原因做全面深入分析,可以为科学评估HIV/AIDS防控措施的效果、预测未来的发展趋势和采取更有针对性的防控措施提供参考。
综上,JPR模型是一种分段线性回归分析方法,可以采用该模型特有的对比分析功能对某些传染病的分组序列数据趋势变化特征进行量化对比分析,为深入揭示疾病的流行规律和开展防控效果评估等提供特定方法,为实施精准防控等提供决策参考。当然,本研究也存在以下主要不足:一是只选用了一个案例进行了分析,代表性有限;二是没有同时采用其他的趋势分析方法进行对比分析。这些有待后续进一步研究。
