季节性ARIMA模型在疑似预防接种异常反应报告趋势预测中的应用*

辽宁省疾病预防控制中心(110005) 常 琳 孙 静 方 兴

【提 要】 目的 建立疑似预防接种异常反应(adverse event following immunization，AEFI)报告病例数的季节性自回归积分滑动平均模型(autoregressive integrated moving average model，ARIMA)，对AEFI报告数进行预测。方法 使用R语言做模型的识别、模型参数的估计、检验，建立季节性ARIMA模型，对辽宁省AEFI报告数进行模型拟合，用2019年1-12月的预测值与实际值作比较，检验模型的预测能力。结果 经过多次检验，确定ARIMA(0，1，1)(1，1，1)12模型预测能力最佳，其残差序列为白噪声。用2019年1-12月数据检验模型，由MAPE的绝对值可以看出，除3月外其他月份预测值与实际值相差均较小，说明模型的拟合优度相对较好，预测结果可靠。结论 季节性ARIMA(0，1，1)(1，1，1)12模型可以较为准确地预测辽宁省AEFI病例报告趋势，可为合理配置AEFI调查诊断所需资源提供理论依据。

近年来，随着扩大免疫规划工作的深入开展，疫苗可控制传染病发病率逐年下降，预防接种后发生的疑似预防接种异常反应(adverse event following immunization，AEFI)逐渐进入了公众的视线，成为媒体关注的重点[1-2]，使得免疫规划工作者将越来越多的精力投入到AEFI处置工作中去。为合理科学地配置AEFI调查诊断所需资源，需要对AEFI病例报告趋势进行科学的预测。

季节性自回归积分滑动平均模型(autoregressive integrated moving average model，ARIMA)模型是由Box和Jenkins于20世纪70年代初提出的一著名时间序列预测方法，所以又称为Box-Jenkins模型。ARIMA模型的基本思想是：将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。ARIMA(p，d，q)模型中AR是自回归，p为自回归项数；MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。季节性ARIMA(p，d，q)(P，D，Q)12模型中，P、D、Q分别表示季节性自回归、差分和移动平均的阶次，以大写与非季节性的p、d、q区分[3]。

材料与方法

1.资料来源

以2009-2019年中国免疫规划信息管理系统中辽宁省境内报告AEFI病例为研究对象，以每月的AEFI报告数构成时间序列。

2.季节性ARIMA模型建模步骤[4]

(1)绘制时序图，掌握序列基本趋势；

(2)通过纯随机性检验考察序列平稳性；

(3)通过一阶差分和季节差分对序列进行平稳化，通过单位根检验验证其平稳性；

(4)通过观察平稳化后序列的自相关和偏自相关图，对模型进行识别和优化，确定d值、p值、q值和P值，D值，Q值；

(5)通过Ljung-Box检验等方法检测模型残差，判断模型的适合性；

(6)利用2019年1-12月AEFI报告数据检验模型的预测效果。

3.统计分析软件

使用R 3.6.1 进行数据分析。采用utils包中的 read.csv函数提取原始数据，采用stats包中的ts函数对原始数据进行时间序列处理，用tseries包中的adf.test函数进行单位根检验，用forecast包中的forecast函数进行预测，用stats包中的box.test对残差序列进行白噪声检验(模型有效性检验)。

结 果

1.时序图绘制及检验

利用stats包中的ts函数绘制时序图(图1)和时序分解图(图2)，由时序图可以看出AEFI人次呈长期增长趋势，为非平稳序列，由时序分解图可以看出原数据受季节因素影响。经Ljung-Box检验后，认为此序列为非白噪声序列(P<0.05)。

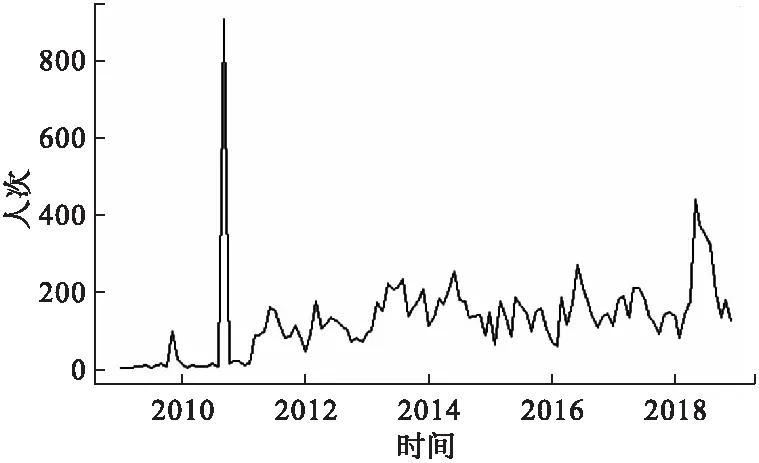
图1 2009-2019年辽宁省报告AEFI人次时序图

图2 2009-2019年辽宁省报告AEFI人次时序分解图

2.时间序列的平稳化

由时序图看出原始时间序列具有上升趋势，所以首先通过一阶差分消除原序列的趋势。随后为了提取原始时间序列的季节性信息，需要对原始数据进行一阶季节差分消除季节趋势。经单位根检验，一阶季节差分序列为稳态序列(P<0.05)，可认为经过一阶季节差分后的时间序列平稳。

3.模型识别

原序列经过一阶差分后，序列的趋势即消除，得d=1；对一阶季节差分序列进行相关和偏相关处理后，得到ACF图(图3)和PACF图(图4)。观察图3，得自相关系数一阶后未超过±2倍估计标准差范围，即自相关系数l阶以后截尾，初步确定q=1；观察图4得偏自相关系数3阶截尾，初步确定p=3。

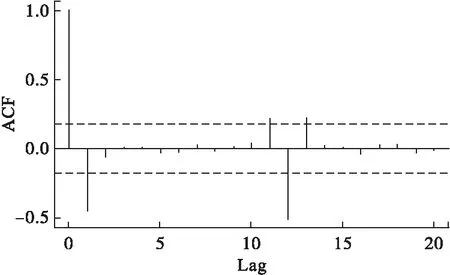
图3 自相关系数图

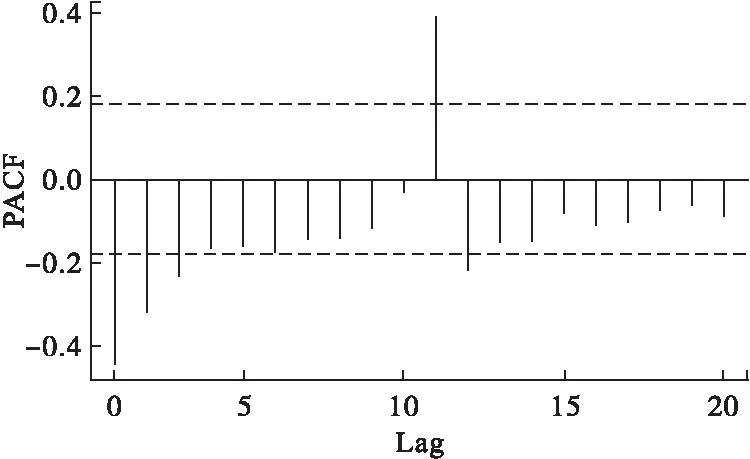
图4 偏自相关系数图

4.模型的参数估计与检验

根据模型参数检验结果和参数间的相关系数，使用auto.arima语句对模型反复调试和检验，以赤池信息准则(AIC准则)作为依据确定最优拟合模型，自动输出相应模型阶数，选择ARIMA(0，1，1)(1，1，1)12模型阶数。对残差序列做自相关图(图5)，观察可知自相关系数值在滞后1期迅速衰减，据此可认为残差序列为白噪声，信息提取较为充分，符合要求。经Ljung-Box检验后，认为此序列为白噪声序列(P>0.05)，该残差序列相互独立。

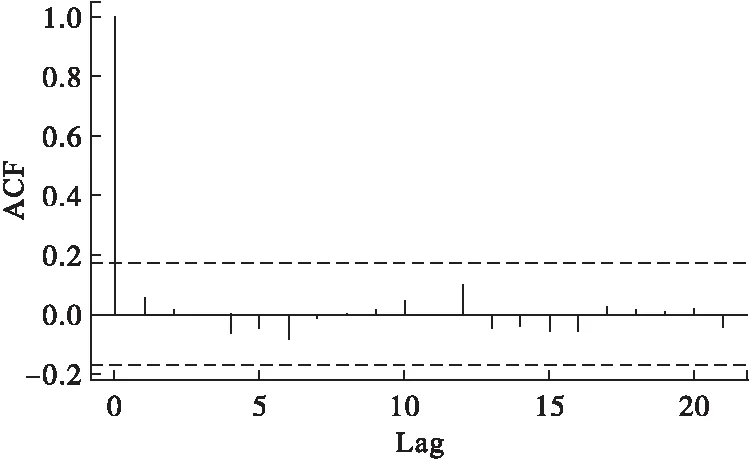
图5 残差序列的自相关系数图

5.预测

利用季节性ARIMA(0，1，1)(1，1，1)12模型对辽宁省2019年AEFI报告数进行预测(图6)，并通过实际报告数对预测结果进行检验，结果显示，该模型的预测值均在95%可信区间内，其平均绝对百分误差(MAPE)仅在3月时较高(42.16%)，提示该模型预测精度可接受(表1)。

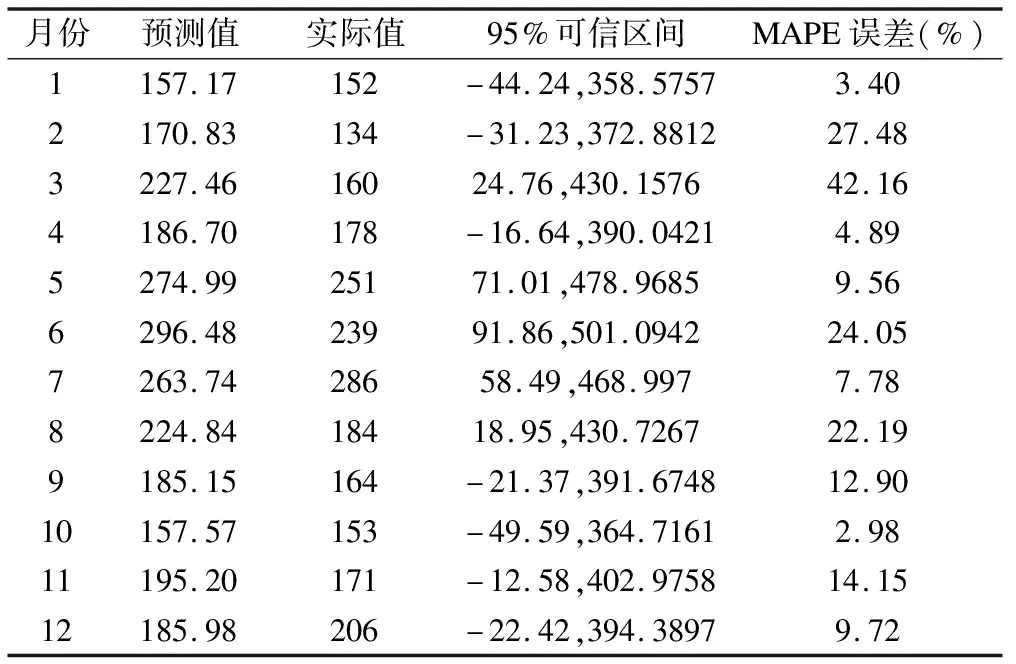
表1 2019年1-12月辽宁省AEFI报告数预测值与实际值及检验

讨 论

AEFI处置包括资料的收集、病例的调查、组织相关专家的讨论、诊断，个别病例可能需要鉴定，AEFI报告情况的预测[5]，对AEFI处置资源的合理配置具有重要指导意义。

调查研究显示，AEFI的报告除了疫苗本身及受种者自身情况的影响外，也受到各种不确定因素及措施的影响。季节性ARIMA时间序列预测模型将各种已知的、未知的因素综合成统一的影响因素蕴含在时间序列变量中[6]。本文建立季节性ARIMA模型将辽宁省2009-2019年AEFI报告数序列分解为趋势、周期、季节和不规则四种不可观测成份后，将原始时间序列中隐含的季节性因素提取出来并予以剔除，消除了不确定因素对时间序列的影响。R作为一种开源免费的软件，具有强大的数据统计处理及图形绘制功能[7]。R软件中的auto.arima语句，可自动根据AIC准则，输出相应模型阶数，避免了根据拖尾和截尾来判断比较主观，不够准确的问题，提高了模型识别效率。

本文使用R软件，经序列平稳化，季节趋势剔除，参数估计、自动识别和检验等步骤建立了辽宁省AEFI报告数季节性ARIMA模型，通过对2019年AEFI报告数的预测及与实际值的对比，认为该模型可较为有效地拟合AEFI报告情况，具有一定的推广价值。但是，由于AEFI报告本身具有一定特殊性，如何将其运用到实际中去，仍是一个值得探讨的课题。