基于湿润锋前进法的不同应力状态砂质黄土土柱渗流试验

蔡国庆，刘倩倩，杨 雨，王华雄，李 舰

（1.城市地下工程教育部重点实验室，北京 100044；2.北京交通大学土木建筑工程学院，北京 100044）

1 研究背景

国内外学者针对饱和土的渗透特性开展了大量研究，而工程界遇到的土体大多呈现可变形的非饱和状态［1-3］。黄土作为一种特殊土，水分入渗会导致非饱和黄土强度降低，并在应力作用下产生湿陷变形，对工程的施工与运营安全造成威胁。因此，研究非饱和黄土在水-力耦合作用下的渗透特性具有重要意义［4］。

现有研究中，通常采用间接法和直接法两种方法确定非饱和土在水-力耦合作用下的渗透系数。间接法是采用土-水特征曲线（SWCC）或其它土体特性来预测非饱和土的渗透性。其中，Leong 等［5］、van Genuchten［6］、Fredlund等［7］提出的渗透系数模型已得到广泛应用。直接法是在实验室或现场直接测量非饱和土渗透系数，包括稳态法、瞬态剖面法和湿润锋前进法等。由于非饱和土渗透试验的试验周期长、试验装置复杂且成本过高等问题，仅有少量学者采用直接法进行研究［8］。Barden 等［9］、Huang等［10］利用稳态法测量土体渗透系数，但试验达到平衡需要较长时间。为进一步缩短试验时间，Meerdink 等［11］、王红等［12］在实验室内利用瞬态剖面法，测定了不同类型土体的非饱和渗透系数，该方法的有效性得到证实，但其测试结果受传感器布设间距和测试时间间隔等因素的影响［13-14］。基于瞬态剖面法，Li等［15］首次提出湿润锋前进法，并利用该方法对五种不同类型土体进行毛细上升和入渗试验，其测试结果表明湿润锋前进法所需的监测截面更少，试验周期更短，可得到较广吸力范围内的渗透函数曲线；李旭等［16］和刘丽等［17］利用试验和数值模拟对湿润峰前进法的适用性和准确性进行了分析；胡海军等［14］对该方法的水力梯度计算公式进行了改进，减少了测得渗透系数的波动性。

非饱和土的渗透性取决于两个应力状态变量，即净应力和基质吸力，它们控制着非饱和土的含水量［18-19］。现有试验研究大多未考虑应力对渗透系数的影响，仅有少数学者分析了非饱和土渗透系数的应力相关性。吴礼舟等［20］通过Fourier积分变化获得非饱和土渗流和变形耦合的一维解析解，表明渗流和变形耦合对非饱和土中的水分入渗产生重要影响。张雪东等［21］建立了变形对土水特征曲线影响规律的预测模型，可利用该模型间接得到变形对渗透系数的影响。C.W.W.Ng等［22］自主研制了一套非饱和土一维渗流装置，采用瞬态法探究了黄土的SWCC 和渗透系数的应力相关性，但该试验忽略了土样的变形。张林等［23］开展了常水头入渗试验，探讨了竖向压力对黄土压缩湿陷特性和入渗过程的影响。张登飞等［24］利用自制的非饱和土三轴渗透仪，探究了孔隙比、等向应力等对非饱和原状黄土增湿渗透系数的影响。由于试验设备的局限性，上述研究未充分考虑应力和干密度对土体渗透及变形特性的影响。

为探究水-力耦合作用下土体的渗透特性，以陕西靖边阳城隧道出口的砂质黄土为研究对象，利用自主研制的水-力耦合试验装置，开展了一系列非饱和砂质黄土渗透系数测量的模型试验。自主研制的试验装置可控制模型试验水流入渗速率、外部荷载大小等边界条件。不同初始干密度的土柱在轴向应力条件下进行渗流试验，利用大量程百分表记录土柱的轴向变形，并采用湿润锋前进法计算得到土体的渗透系数。模型试验重点研究了不同干密度下非饱和砂质黄土在水-力耦合作用下其渗透及变形特性的演化规律，并揭示了水-力耦合作用下非饱和土渗透特性演化的内在机理。

2 试验原理

采用Li等［15］提出的湿润锋前进法（WFAM）确定非饱和砂质黄土在不同竖向应力作用下的渗透系数k。针对一维圆柱形干燥土样，开展自上而下的渗流试验，湿润锋定义为干燥与湿润土样之间的分界线（图1）。在入渗过程中；土柱逐渐湿化，湿润锋位置随时间不断下移。通过连续记录湿润锋位置、含水率和吸力随时间的变化，得到土柱渗透系数。其计算公式为：

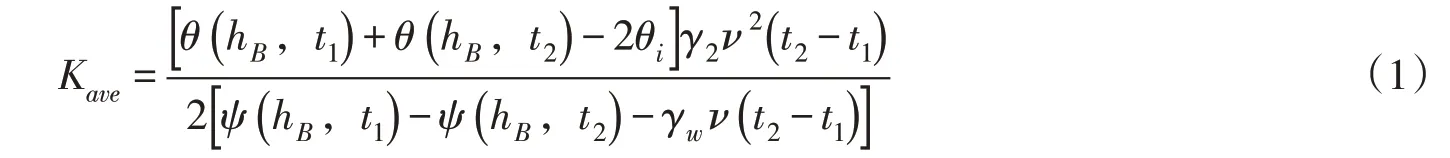
式中：Kave为t1时刻与t2时刻的平均渗透系数；hB为任意水分传感器至土柱顶部的距离；为hB位置处在t1时刻的体积含水率；为hB位置处在t2时刻的体积含水率；θi为初始体积含水率；γw为土体重度；ν为湿润锋前进速率；为hB位置处在t1时刻的基质吸力；为hB位置处在t2时刻的基质吸力。

与稳态法、瞬态剖面法等常用渗透系数测量方法相比，WFAM适用于黏土、粉土和砂土等多种类型土体，具有试验周期短、吸力范围广和监测面少等特点，在试验装置设计上有更大的适应性。但该方法要求试验土体具有明确的干湿界限，试验中采用的砂质黄土满足上述要求（图1）。

图1 湿润锋位置

3 模型试验

3.1 试验装置为探究水-力耦合作用对土体渗透系数的影响，自主研制了一套非饱和土渗透系数的测量装置如图2所示。该装置主要包括土柱容器，加载装置、量测系统和供（排）水系统。

土柱容器由两个500 mm高的亚克力空心筒组成，其内径和外径分别为150 mm和160 mm。试验中土柱设计高度为800 mm，土柱的纵横比大于5，满足一维渗流要求［15，22］。土柱一侧贴有带刻度的标尺，另一侧在距离土柱顶部高度分别为200 mm、350 mm、500 mm和650 mm处开孔，便于安装水分传感器。

该装置的突出特点是可以控制一维土柱渗流试验的边界条件。土柱容器顶部连接加载装置和供水系统，分别控制轴向力和水流流量。加载装置采用气动加载，加载杆与土柱顶部的多孔铝板中心相接触，将轴向力均匀地传递到压实土中。土柱轴向位移可由容器顶部大量程百分表确定。供水装置与马氏瓶类似，通过为渗流试验提供恒定水头来控制渗流速度。土柱底部固定在钢制底座上，中间有直径10 mm的水流通道，便于排水。当湿润峰到达土柱底部时，水分流出土柱，进入容器底部的储水水箱。

量测系统用于测量试验过程中产生的数据，主要有以下4部分：（1）土柱容器顶部安装大量程百分表，用于确定土柱加载以及湿化过程中的轴向位移；（2）土柱容器一侧的刻度尺用于记录湿润锋随时间的变化；（3）在土柱容器开孔处安装4个EC-5水分传感器，利用已测得的传感器标定曲线，将传感器电信号转换成相对应的体积含水率，得到各截面的含水量随时间的变化；（4）上部和下部水箱重量变化由电子秤测量，可得入渗水量和流出水量。

图2 水-力耦合试验装置

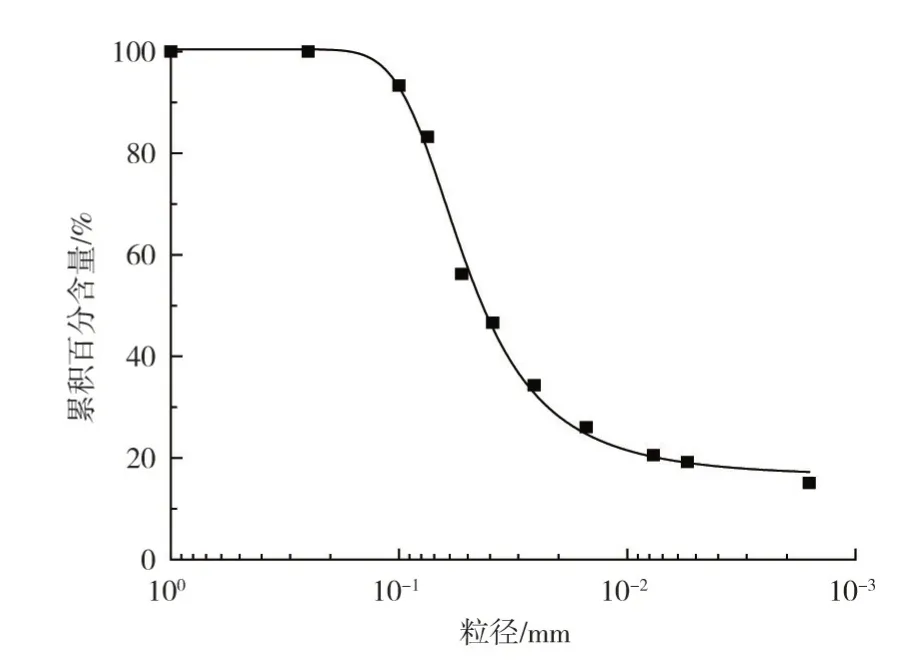
图3 黄土颗粒级配曲线

3.2 试验用土试验用土是取自陕西靖边阳城隧道的砂质黄土，利用轻型击实仪测得砂质黄土最优含水率为12.5%，最大干密度为1.81 g/cm3。试验中测得的其他基本物理性质指标如表1所示。采用筛分法和密度计法测得其颗粒级配曲线如图3所示。经计算，该土样不均匀系数Cu=7＞5，曲率系数Cc=5.71，为级配不良的不均匀细粒土。

表1 黄土基本物理性质

3.3 试验方案为探究不同初始干密度的砂质黄土在应力作用下的水-力耦合特性，试验土柱的初始干密度分别设置为1.40 g/cm3、1.55 g/cm3和1.65 g/cm3。在每个干密度条件下，分别为土柱施加0 kPa、40 kPa和80 kPa大小的轴向力，总共进行了9组试验。水-力耦合作用下非饱和土渗透函数测量试验主要由两部分组成：（1）不同干密度黄土的土-水特征曲线（SWCC）测量试验；（2）水-力耦合作用下土柱渗流试验。

3.3.1 土-水特征曲线 为探究干密度分别为1.40、1.55和1.65 g/cm3砂质黄土的持水特性，采用张力计法、滤纸法和冷镜露点法三种方法进行吸力测量，可较为准确地得到全吸力范围内的土-水特征曲线。

图4 吸力测量方法

如图4（a）所示，采用2100F张力计测量低吸力范围段（0～100 kPa）的SWCC，利用自制容器配制各个干密度不同含水率的土样，土样直径100 mm，高50 mm。为减小试验误差，同时使用两个张力计进行测量。高吸力范围（＞4000 kPa）采用图4（b）所示的露点水势仪（WP4C）测量，测试样品由特定模具制作，直径35 mm，高5 mm。接触式滤纸法（图4（c））原则上可测量全范围的基质吸力，但由于环境因素以及试验操作限制，其准确性在高吸力以及低吸力段较差，因此利用该方法补充SWCC曲线中间试验点。

利用VG 模型［6］（式（2））对SWCC 试验数据进行拟合，得到砂质黄土在不同干密度下的SWCC如图5所示。

VG模型：

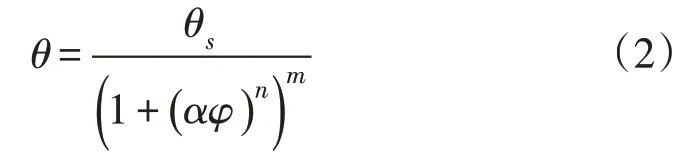
式中：θ为体积含水率；θs为饱和体积含水率；φ为基质吸力；α、m和n为拟合参数，所有拟合参数数值见表2。

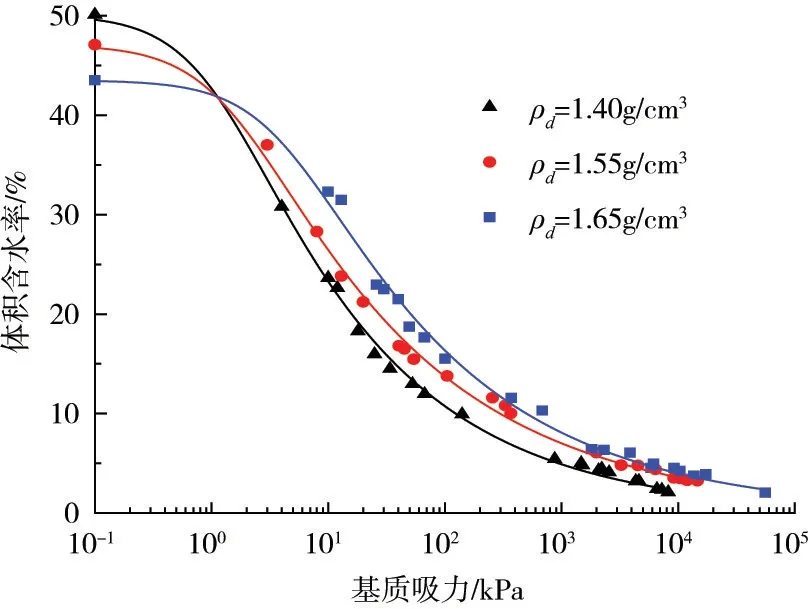
图5 不同干密度下黄土的土-水特征曲线

表2 黄土土-水特征曲线拟合参数

由图5可知，砂质黄土的基质吸力与体积含水率呈负相关。随着干密度增加，饱和含水率减小而进气值逐渐增大，这与张雪东等［25］的论述相符合。

3.3.2 水-力耦合作用下土柱渗流试验步骤 试验主要分为以下4步：（1）试样制备。土柱设计高800 mm，直径150 mm，根据给定干密度计算出所需烘干土样的重量。在土柱容器内，将烘干土样分20层逐层击实，每层土样的击实高度为40 mm。在容器开孔处，利用特制模具在击实土柱上掏出孔洞，再装入水分传感器。（2）加载。装样完成后，对土柱施加荷载。荷载分级加载，每级荷载大小为10 kPa。当土柱轴向变形稳定后（轴向变形量＜0.01 mm/h）施加下一级荷载，直至目标荷载。（3）湿化。加载至目标荷载且土柱轴向变形稳定后，打开马氏瓶阀门，同时启动秒表。每间隔一定时间记录上部电子秤读数、百分表读数、湿润锋前进位移。（4）拆样。土柱底部出水后每间隔一定时间记录底部电子秤读数，当土柱底部出水稳定时（电子秤读数变化小于1 g/h 且至少持续24 h），水-力耦合渗流试验结束。

4 试验结果分析

4.1 湿润锋前进速率采用湿润锋前进法（WFAM）开展了在水-力耦合作用下的一维土柱渗流试验，得到初始干密度分别为1.40 g/cm3、1.55 g/cm3和1.65 g/cm3的土柱在不同荷载作用下湿润锋高度随时间的变化如图6所示。每次试验中，湿润锋初始高度为零。当湿润锋到达土柱底部时，说明整个土柱已经湿润，对应的时间为完全湿化时间。

图6 不同干密度下湿润锋前进位移随时间变化关系曲线

由图6可得，在相同初始干密度条件下，当轴向力p由0 kPa变化到80 kPa时，土柱完全湿化时间增大。这是由于荷载作用下，土柱产生竖向压缩，干密度增大，土体内部闭合孔隙增多，阻碍了水流入渗。另外，对比图6（a）（b）（c）可得：轴向力相同时，土柱完全湿化时间随着初始干密度的增加而增加；随着初始干密度的增加，轴向力对土柱湿化的影响逐渐减弱。例如，初始干密度为1.40 g/cm3时，轴向力分别为0 kPa和80 kPa的完全湿化时间相差约200 000 s，而初始干密度增加至1.65 g/cm3，该差值缩小至100 000 s。表明初始干密度为1.65 g/cm3时，轴向力引起的干密度变化较小，土柱压缩已接近极限。

利用数据处理软件对图6数据进行拟合，湿润锋位移与时间呈现幂函数关系：

式中：y为湿润锋位移；t为时间；a和b常数，拟合参数见表3。

表3 湿化位移随时间变化拟合参数

对式（3）求导得到湿润锋速率随时间变化呈现对数关系：

式中：v为湿润锋速率；t为时间；λ和c为常数。

由式（4）可得不同干密度条件下湿润锋速率随时间变化关系（图7）。在不同初始干密度和轴向力作用下，土柱湿润锋速率随着入渗时间的增加而减小，并在入渗后期逐渐趋于一致。这是由于土样与容器之间存在不可避免的摩擦力，在荷载作用下，表层土体变形较大，深部土体变形较小，土柱干密度分布不均，导致湿润锋速率前期差异较大而后期趋于一致。

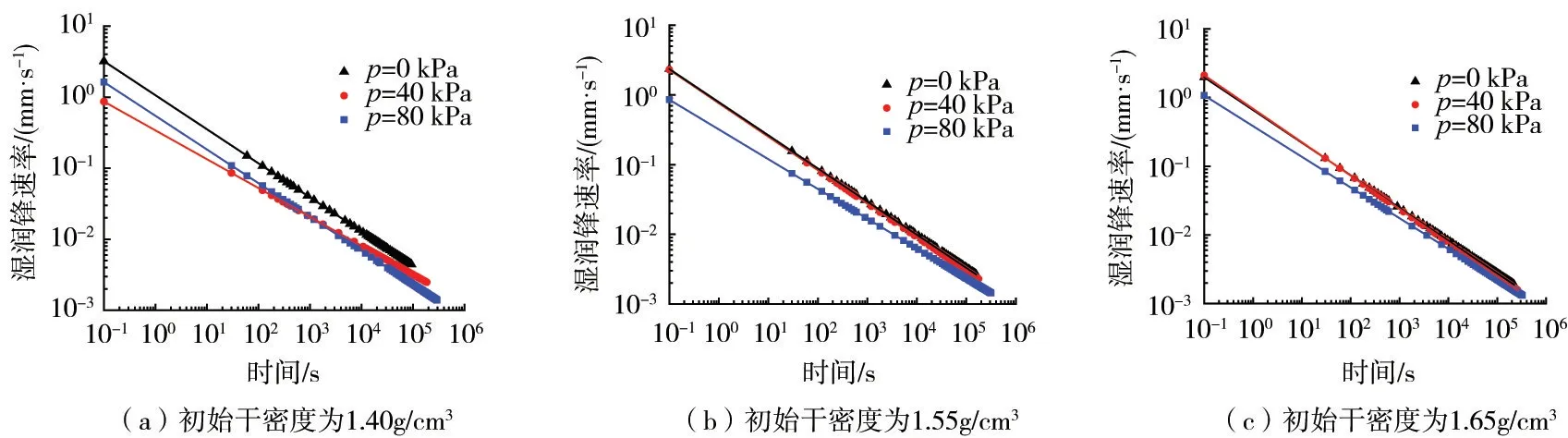
图7 湿润锋速率随时间变化曲线

图7（a）中，轴向力40 kPa时初始阶段的湿润锋速率略小于轴向力80 kPa时的湿润锋速率。这是因为初始干密度较小的土柱开始湿化时，表层土壤的不均匀性对湿润锋前进速率产生一定的影响，随着入渗深度增加，这种影响逐渐消失。由图7可知，初始干密度和轴向力均会导致湿润锋速率发生改变，而轴向力对湿润锋速率的影响，本质上是通过改变土体干密度实现的。这说明土体干密度是影响湿润锋速率的主要因素。

4.2 水-力耦合作用下砂质黄土渗透系数为探究砂质黄土在水力耦合作用下的渗透特性，开展了九组一维土柱渗透试验。在入渗过程中，假定在水分传感器周围土体在由干变湿时，土体变形量忽略不计。因此，可利用不同干密度条件下砂质黄土的SWCC，得到不同含水率所对应的基质吸力。该假定基于以下3个原因：（1）传感器周围土体由干燥变为接近饱和状态的时间较短，土体在短时间内未发生较大变形；（2）土柱湿化变形集中在湿化的初始阶段，变形速率随湿化时间增加而减小；（3）由于土体和容器间不可避免的摩擦力，加载变形主要发生土柱表面，传感器周围土体的干密度变化较小。

由式（1）计算得到不同初始干密度砂质黄土的渗透系数如图8—10所示。在不同初始干密度和轴向力作用下，渗透系数随基质吸力增加而减小。图8是初始干密度为1.40 g/cm3时，不同轴向力作用下不同测试截面的渗透函数曲线。可以看出，不同截面处渗透函数曲线呈现明显的分层现象，且分层性随轴向力增大而增大。例如，当轴向力为80 kPa时（见图8（c）），同一基质吸力下渗透系数最大值和最小值相差接近一个数量级。这是由于轴向力作用下，土柱各截面干密度分布不均。

图8 初始干密度为1.40 g/cm3时不同轴向力下渗透系数函数

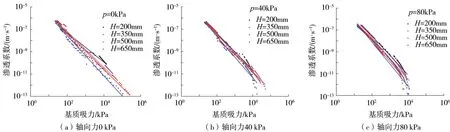
图9 初始干密度为1.55 g/cm3时不同轴向力下渗透系数函数

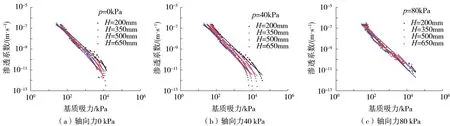
图10 初始干密度为1.65 g/cm3时不同轴向力下渗透系数函数

初始干密度为1.55 g/cm3时（图9），渗透函数曲线分层现象与图8类似，在相同轴向力作用下，各个剖面处渗透系数曲线的分层现象随着基质吸力增加而越发显著。当初始干密度增加到1.65 g/cm3时（图10），渗透系数曲线分层现象减弱。

对比图8—10中数据可知：（1）土体渗透系数随基质吸力的增加而减小；（2）不同测试截面处渗透函数曲线出现分层现象，相同初始干密度条件下，随着轴向力的增加分层现象越发显著；（3）土体初始干密度和轴向力越大，土体渗透系数越小。上述试验结果表明，轴向力作用下，由于土体和容器间不可避免的摩擦力，土柱不同高度处的密度不同，导致不同剖面处测得的渗透系数函数不同；随着土柱初始干密度的增加，试验中土柱干密度受到轴向力的作用逐渐减小，因而轴向力对非饱和土渗透系数影响效果减小。该结果与湿润锋速率相一致。

当湿润锋到达土柱底部，且至少24 h 内出水速率小于1 g/h，认为土柱达到稳定渗流，由Darcy定律可得稳定渗透系数如图11所示。同一初始干密度下，稳定渗透系数随轴向力增大而减小。例如，初始干密度为1.40 g/cm3时，空载（即轴向力为零）土样稳定渗透系数约为9.36×10-7m/s，是轴向力80 kPa 土样稳定渗透系数的4.27 倍。另外，轴向力由0增大到80 kPa时，不同初始干密度土柱的稳定渗透系数趋向一致。这是由于轴向力越大，加载后各个土柱的表层密实度大致相同，稳定渗流速率大小相近。

图11 土柱稳定渗透系数与轴向力关系曲线

4.3 轴向位移水-力耦合渗流试验中，对土柱施加轴向力，待变形稳定后，对土柱进行湿化。土柱在轴向力和湿化共同作用下体积减小，产生轴向压缩，因此土柱轴向位移可分为湿化前位移和湿化后位移两部分。

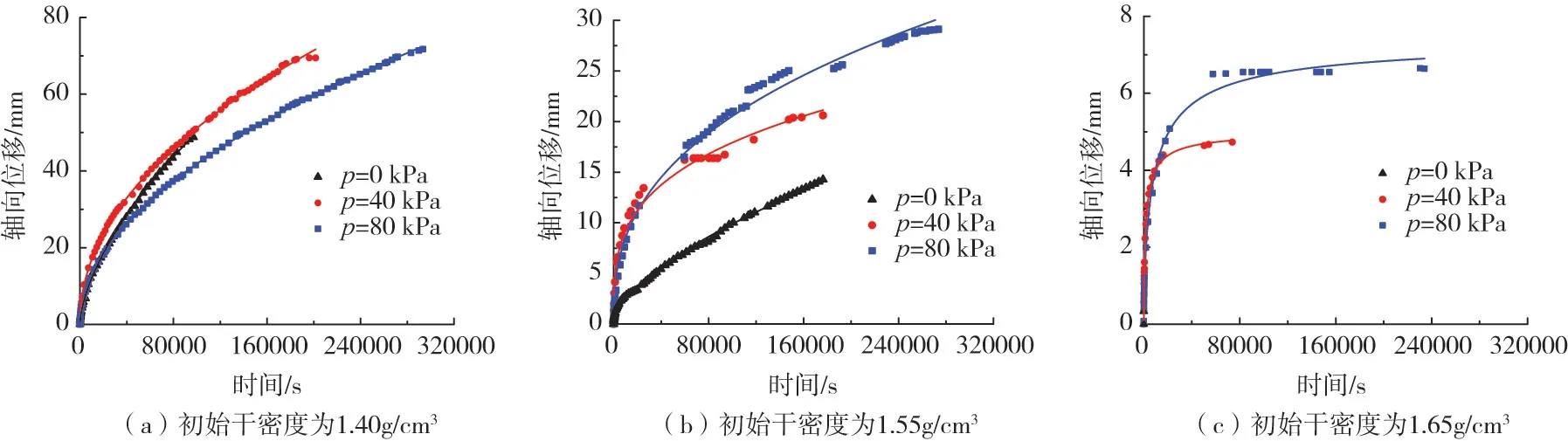
图12 不同干密度下土柱湿化后位移随时间变化曲线

图12是湿化后位移随时间的变化。由图可知，在湿化过程中，土柱轴向位移随时间的增加而增大，但增长速率逐渐减小。在轴向力p恒定时，轴向变形随初始干密度的增大而减小。当试件处于空载状态时，初始干密度为1.40 g/cm3与1.65 g/cm3的土柱轴向变形之比约为147。可见，初始干密度越大，土柱越难压缩。另外，轴向力的增加对湿化后位移也有显著影响。例如，在初始干密度为1.40 g/cm3时，当轴向力由0 kPa 增加至80 kPa，轴向位移增加了22.97 mm。

图13 土柱湿化前后位移对比曲线

在土柱湿化前，对土柱施加荷载，土柱变形通常在较短时间内即达到稳定，因此仅记录湿化前的稳定位移值。土柱湿化前后稳定位移与轴向力p的关系如图13所示。湿化前，初始干密度较小的土柱轴向位移较大，干密度较大土柱变形不明显。由此可见，当初始干密度较大时，处于干态的砂质黄土具有较高的强度，不易被压缩。湿化完成后，各试样的轴向位移变化较大。以上数据表明，砂质黄土具有较大的水敏性，在水-力耦合作用下土体结构破坏，导致湿化前后轴向位移差异较大。

5 结论

阳城隧道开挖过程中，内部砂质黄土遇水浸湿。在自重和附加应力作用下，土体的变形和渗流处于动态变化中。探究水-力耦合作用下砂质黄土的变形和渗透特性，对指导隧道施工和安全运营起到积极有效的作用。利用自主研制的水-力耦合试验装置对砂质黄土进行了一系列一维垂直渗透试验，得到水-力耦合作用下非饱和土渗透系数的演化规律。主要有以下结论：（1）在不同初始干密度和轴向力作用下，土柱湿润锋速率随着入渗时间的增加而减小，并在入渗后期逐渐趋于一致；（2）砂质黄土的渗透系数随基质吸力的增大而减小。在不同测试截面处，渗透函数曲线出现分层现象。相同初始干密度条件下，随着轴向力的增加分层现象越发显著；（3）初始干密度或轴向力的增大均会导致渗透系数减小，而轴向力对土体渗透性的影响是通过改变土体干密度实现的。这说明土体干密度是影响渗透性的主要因素；（4）砂质黄土具有较大的水敏性，在水-力耦合作用下土体结构破坏，导致湿化前后轴向位移差异较大。

水-力耦合特性是非饱和土区别于饱和土的重要特性之一。尤其在土质堤坝防渗、核废料处置库污染物迁移、隧道围岩支护等工程中，分析水-力耦合作用下土体的变形及渗透特性尤为重要，值得进一步开展相关研究。