基于蚁群算法的光伏并网逆变器孤岛检测

王 猛, 李梦达, 王星皓

(上海电机学院 电气学院, 上海201306)

近年来可再生能源所占比例逐年递增。分布式发电利用风能、光能等可再生能源,具有环境友好、可循环利用等优点。但由于发电系统靠近用户侧,一旦与电网断开,容易形成一个自给的网络,是为孤岛效应。而非计划性孤岛的发生,对用户端而言,会损坏用电设备中的敏感负荷,并使电能质量无法满足要求;对电网端而言,则会威胁电网维护人员安全。因此,近年来行之有效的孤岛检测方法成为研究热点[1-3]。

孤岛检测的方法可分为远程检测和本地检测两大类[4]。远程检测由于通信干扰和造价过高,不适用于小型系统。本地检测可分为被动式和主动式检测[5]。被动式检测由于存在检测盲区(Nondetection Zone,NDZ)的原因,检出率很难达到100%;而主动式检测由于注入了扰动,会造成谐波畸变,影响电能质量[6]。刘芙蓉等[7]提出了极端条件下主动频率偏移法(Active Frequency Drift,AFD),实现无NDZ需要的约束条件并给出了相关参数的优化。邹培源等[8]提出了基于模糊控制的滑模频率偏移孤岛检测方法,能够有效减小NDZ。但当负载负荷相频曲线倾斜幅度大于滑模频率曲线时,会发生漏检。孙振奥等[9]提出了一种新的截断系数控制策略,用以兼顾电能质量和检出效率。该方法的正反馈系数能根据负载性质的不同进行正反两个方向的偏移,但其大小无法针对不同的偏移程度进行自适应改变,难以实现精准控制。王康仲等[10]提出了基于模糊控制的AFD法,减少了电流谐波畸变率,缩短了检测时间,但并未对模糊控制器本身进行优化。

本文针对文献[10]所提的模糊控制器存在隶属度函数单纯依靠专家经验和控制规则冗余等问题,提出一种改进的蚁群算法用于优化模糊控制器。将模糊控制器的隶属度函数、模糊控制规则、以及比例因子、量化因子分为3个种群,给定搜索空间和同一个目标函数。当迭代至一定代数以后,目标函数将趋于稳定,找出最优解对应的隶属度函数和模糊规则,从而生成模糊控制器,使其能够根据公共耦合点(Point of Common Coupling,PCC)电压和逆变器输出电流的频率、相位误差自适应地调整正反馈系数,从而达到检测的目的[11]。

1 无NDZ的实现

当电网与负载断开后,若逆变器没有断开,则分布式电源向负载持续供电,PCC在产生波动后达到新的平衡,此时应满足的负载相角关系为

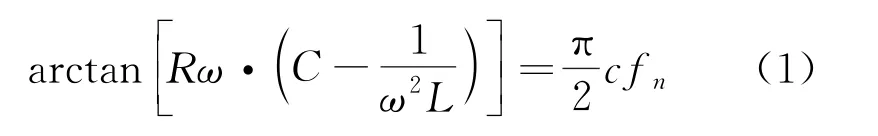
式中:ω为PCC电压角频率;R、L、C分别为并联负载的电阻、电感和电容;cf n称为主动频移法的截断系数(下标n代表当前时刻),反映电流频率偏移电压频率的程度。

设电网电压角频率为ω0,Δω为PCC电压频率与电网电压频率差值,Cres为谐振电容,则

为了表达方便,用负载电容的标值CN代替C,替代后有

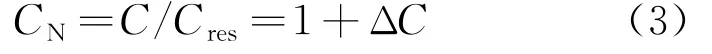
式中:(1+ΔC)为负载电容与谐振电容比值。

将式(2)、(3)代入式(1),可得

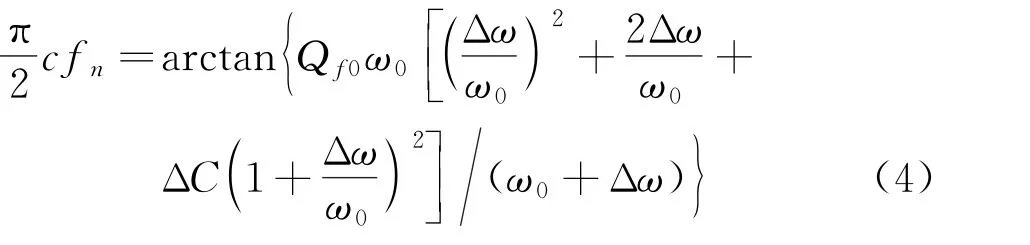
式中:Q f0为孤岛检测中设定的品质因数。

频率检测的阈值为±0.5 Hz,额定电网频率为50 Hz,与ω0相比,Δω的数值很小,可将式(4)变为

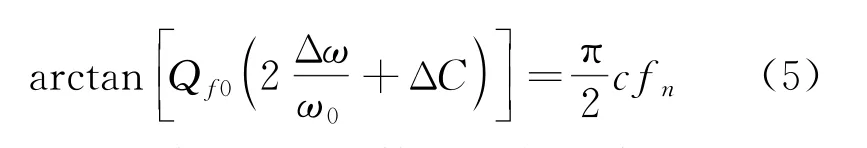
由式(5)可知,品质因数Q f0与电容ΔC一旦确认下来,截断系数cf n决定了频率偏移量Δω的大小。如果断网后Δω的数值始终小于阈值,则孤岛检测失败。而根据主动频移法的定义,截断系数的表达式为

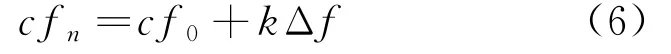
式中:k为正反馈系数;cf0为初始截断系数,用来在孤岛时加速频率偏移。

将式(6)代入式(5),有

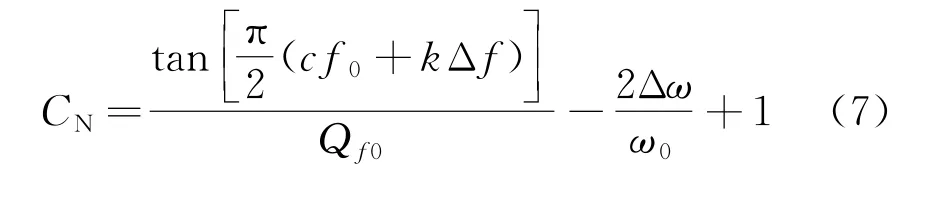
从式(7)可以看出,当坐标系取为CN×Q f0时,cf0和k的取值是导致NDZ位置变化的变量,这里将角频率波动的上下限Δω+、Δω-分别代入式(7),得到NDZ边界和,如图1所示。其中图1(a)为不同k下的NDZ,图1(b)为不同cf0下的NDZ。

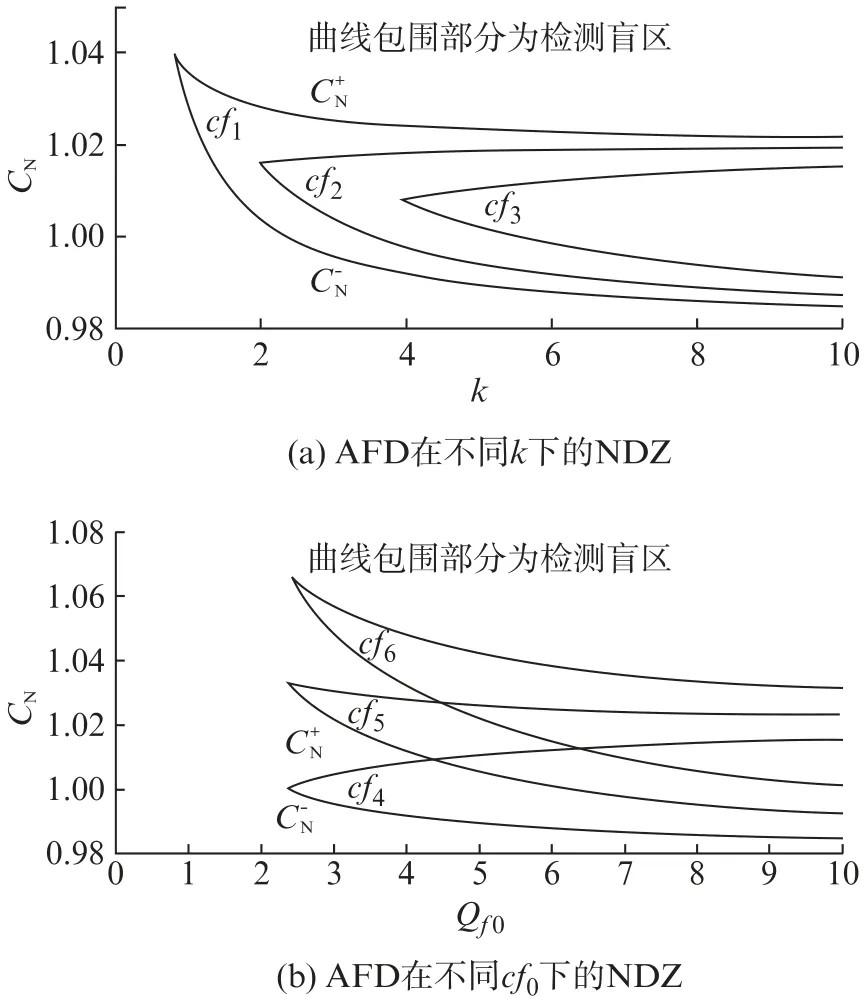
图1 AFD在不同因素下的NDZ

图1中:cf1=0.02+0.02Δf,cf2=0.02+0.05Δf,cf3=0.02+0.1Δf,cf4=0.06Δf,cf5=0.05+0.06Δf,cf6=0.1+0.06Δf。从图1可以得出以下结论:

(1) 曲线包围区域为NDZ。NDZ主要分布在CN=1附近,当负载的谐振频率为工频50 Hz时,检测失败的可能性最大;

(2) 由图1(a)可知,k的取值影响NDZ的面积:k取值越大,NDZ向右移动幅度越大,NDZ面积越小,反之,NDZ面积越大;

(3) 由图1(b)可知,初始截断系数cf0对NDZ的面积影响不大,仅使其上下移动。

为了满足负载的合理性[12],负载的品质因数Q f≤2.5。当角度很小时,tanθ≈θ,若检测无盲区需满足,对式(7)进行变换,求出k的取值范围,有

根据式(8),在Q f0=2.5,f=50 Hz的极端情况下,要使检测无盲区,需满足:k＞0.063 7。而初始截断系数cf0由于其大小对NDZ宽度基本无影响,且影响逆变器输出电流电能质量,其作用为断网时可以有效触发扰动动作,绝对值应较小[13]。

2 模糊控制器的设计及改进

2.1 模糊控制器的设计

由cf n的定义可知,k的大小无法改变,为了兼顾注入扰动对电能质量的影响和检测时间之间的矛盾,需要k自适应地变化:当电网正常时,在电网电压钳制作用下,PCC电压频率偏差e和频率偏差率ec基本保持不变,k输出为一小值以免发生误动;而当电网与负载之间连接断开时,由于失去钳制作用,则输出k值较大,这一较大的cf n影响PCC电压频率持续偏移,直至超出阈值后逆变器与负载断开。

上述控制策略的实现需要一个二维的模糊控制器,其输入量为e以及ec,输出量为k。在模糊控制器中制定相应的模糊控制规则,根据制定的规则自适应地选取最优k。模糊控制器的系统如图2所示。

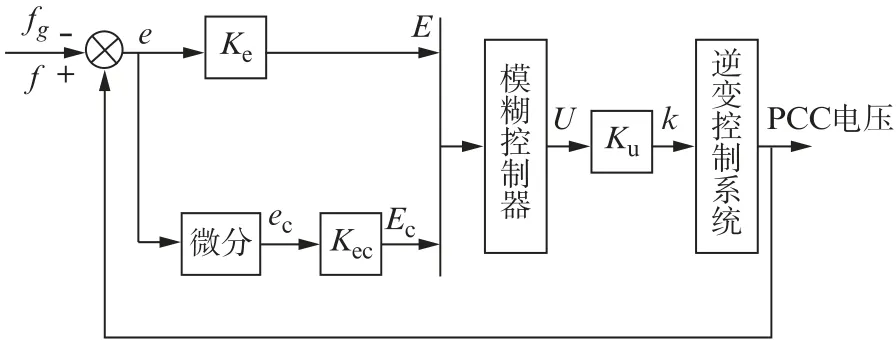
图2 模糊控制器的系统

图2中,f表示输入频率,fg表示给定频率50 Hz,E表示乘以比例因子Ke后的输入量e,Ec表示乘以比例因子Kec后的输入量ec。经过大量实验证明[14],e的合理阈值为±0.5。令e∈[-0.5,0.5],那么ec∈[-50,50]。经过对k值的推导及大量的仿真数据验证,k的范围取为[0.1,5.6]。则e、ec、k相对应的模糊集为图2中的E、Ec和U。定义E和Ec的论域为[-6,6],U的论域为[0.1,5.6],将E、Ec两个子集的论域都分为7档:{NB(负大)、NM(负中)、NS(负小)、ZE(零)、PS(正小)、PM(正中)、PB(正大)};U子集的论域与输入相同,也分为7档:{ZE(零)、SS(较小)、S(小)、M(中)、BB(较大)、B(大)、VB(极大)}。那么由参数的取值范围和论域可知,比例因子Ke=6,Kec=0.06,Ku=1。模糊控制采用T-S模型,控制规则如表1所示。

表1 模糊控制规则表

当确定适用的T-S模糊规则后,采用重心法求解并乘以量化因子Ku,得到k,并选用mamdani型控制器。

2.2 模糊控制器的优化

为了更精准地实现模糊控制,隶属度函数、模糊控制规则的选取不能仅依靠专家经验获得。遗传算法在解决单目标路径优化问题时,可以对离散变量在有限求解运算中得到最优解,在路径规划问题中使用较为广泛。但本身构造所带来的局限性,使其在解决多目标组合最优路径的规划问题时出现早期收敛和遗传偏移的现象。这些问题的出现是其本身的框架所决定的。由于问题空间和遗传操作空间存在一定耦合,其编码-交叉操作生成的染色体将在问题空间出现,成为致死个体。

粒子群算法由于其对初始值有一定要求,一旦初始值选取不够合理,最终将无法振荡收敛。而在模糊控制的优化中,初始值的选取是随机的,故该方法对于模糊控制器的优化效果并不明显。

蚁群算法同样适用于路径优化问题,且对多目标优化问题可以通过多种群共同进化进行求解,对于模糊控制模型的改进在理论上是可行的,关键在于每个种群的构建及目标函数的选取。

本文选择蚁群算法对模糊控制器中各参数进行优化,提出了一种基于蚁群算法的改进方法,并将其用于优化模糊控制器:将隶属度函数、模糊控制规则以及比例因子、量化因子分成3个独立的种群,共用同一个目标函数J,这里定义J为10个电网周期内误差的累积量,有

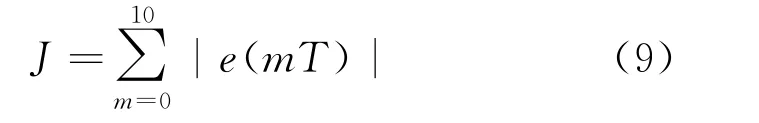
式中:T为采样周期;m为采样时刻。

算法的实现包含了初始化和路径构建两大部分。其中,初始化包括位置初始化和信息素的初始化两大类。隶属度函数采用三角形隶属度函数,为了保证其语义性和完备性,不再采用每个三角形左右端点和顶点作为初始点,而是对顶点bi、重叠因子αi和右跨度系数r i进行编码。以连续的两个隶属度函数PS、PM 为例,如图3所示。

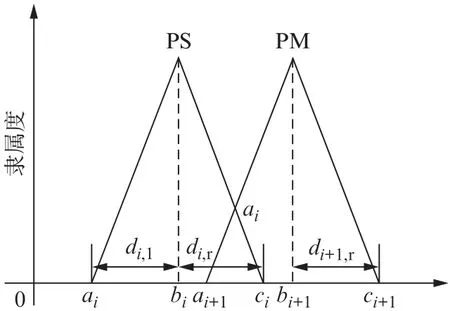
图3 三角形隶属函数编码

在图3中,横坐标表示宽度,为一标量;纵坐标表示隶属度;a、b、c表示三角形的3个顶点;d i,l和d i,r分别表示第i个三角形隶属函数的左跨度和右跨度。

定义右跨度系数为

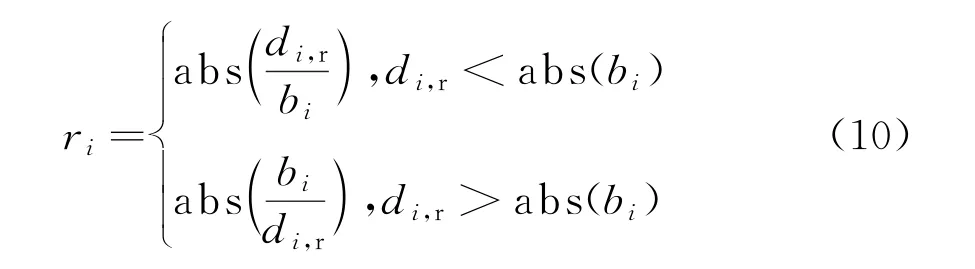
根据相似三角形之间的关系,推导出左宽度为

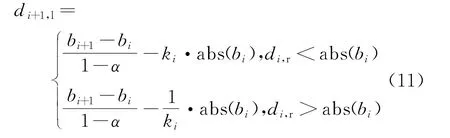
根据式(10)和式(11)就可以求得三角形隶属度函数的3个端点,其中r i∈(0,1),αi∈[0.3,0.8],整个种群待优化的参数有21个。模糊控制规则表的初始化按表1,为7×7的规则表,分别用表示7个模糊变量。

由于搜索空间是离散的,算法路径的构建将经典蚁群算法轮盘赌选择方式进行改进,有

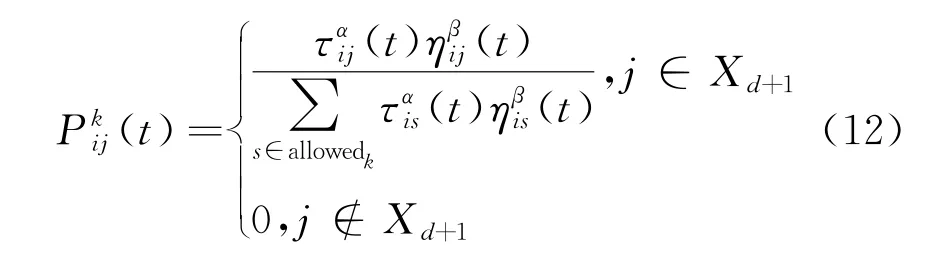
式中:P ij为节点i转移到节点j的概率;allowed表示在禁忌表之外的空间集合;ηij为从节点i转移到节点j所生成目标函数J的差值;τ为信息素浓度;α、β为启发因子,表示两者的重要程度。

路径的构建完成后,在第一轮迭代完成时,需要对后续迭代的信息素浓度进行更新,有

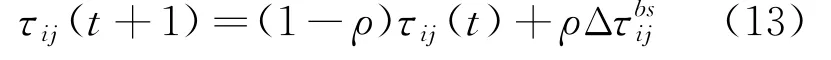
式中:0＜ρ＜1为信息素衰减系数;为节点i转移到节点j目标函数差值的倒数。

蚁群算法的基本步骤流程如图4所示(nc为迭代数)。

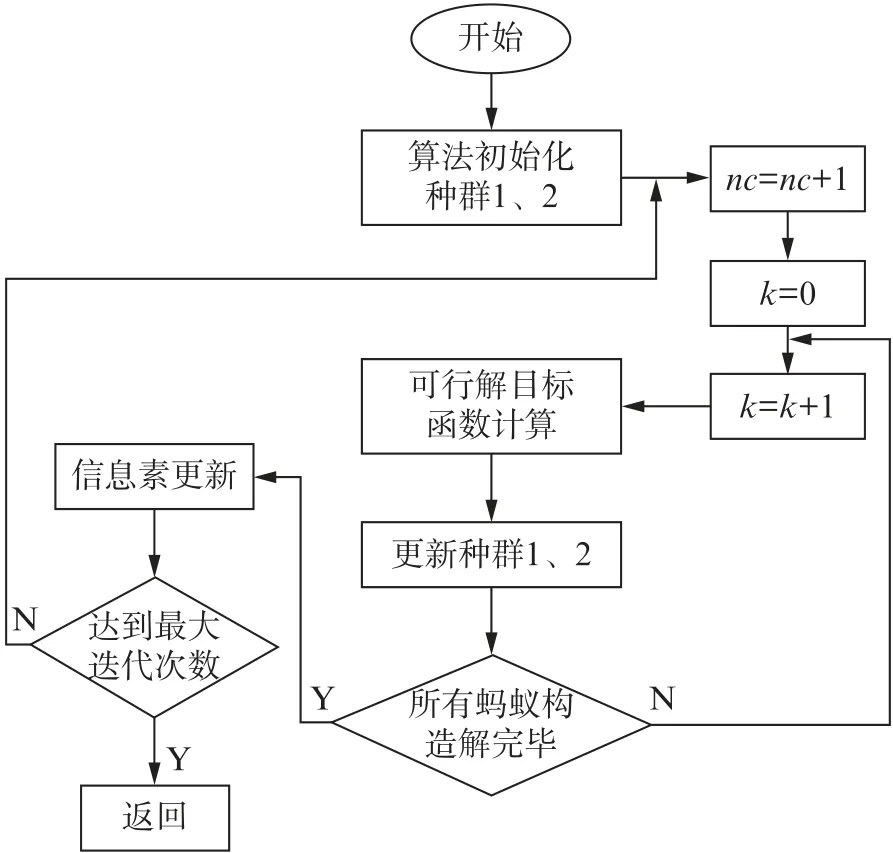
图4 蚁群算法流程

3 仿真建模及硬件系统设计

3.1 仿真结果分析

为了验证所提算法的有效性,本文通过在Matlab/Simulink仿真平台上搭建主电路及控制电路的仿真模型,对传统的正反馈AFD、模糊优化后的正反馈AFD以及加入蚁群算法优化后的正反馈AFD进行仿真实验。其中,蚁群算法的优化利用计算机编程实现。模型中的具体参数如表2所示。

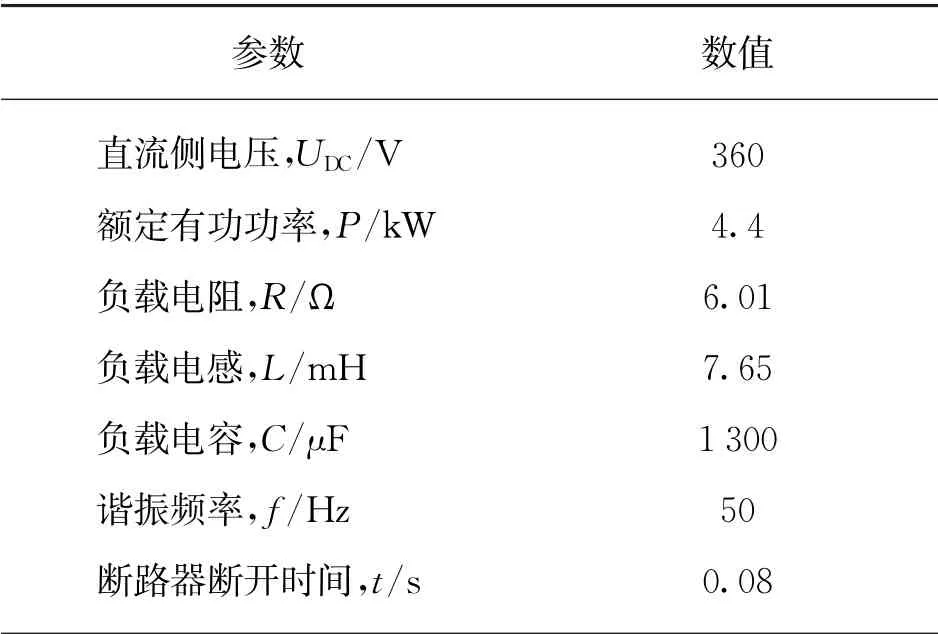
表2 Simulink仿真模型参数表

由图1(a)可知,当谐振频率与电网频率相同时,检测失败的可能性最大;且根据IEEE—929规定,负载Qf最大值为2.5,即对Qf≤2.5的负载组合,只要实现无NDZ即可。综上所述,仿真选取最恶劣情况下的负载组合:负载谐振频率为50 Hz,负载品质因数为2.5,其他仿真参数如表2所示,设置最大迭代次数为200,目标函数进化曲线如图5所示。

从图5可以看出,经过85次迭代后系统目标函数超过了0.5(0.509 3),这时将触发过频保护,若继续增大则会进一步影响电能质量,函数已趋于稳定,优化过程结束。

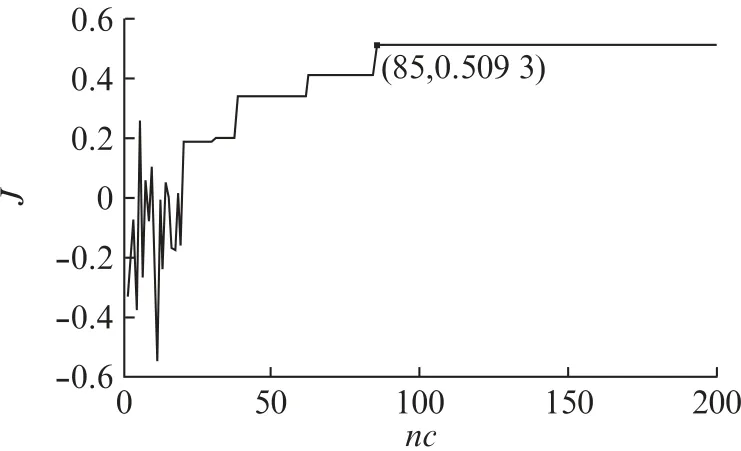
图5 目标函数进化曲线

控制器达到最优效果后,将输出的三角形隶属度函数效果与改进前相比较,具体如图6所示(纵坐标为0～1之间的连续实数,用来表示隶属度的大小)。

图6(a)是未优化的e和ec;图6(b)是蚁群算法优化后的e;图6(c)是蚁群算法优化后的ec;图6(d)是在蚁群算法优化后的e、ec以及控制规则作用下的输出u。

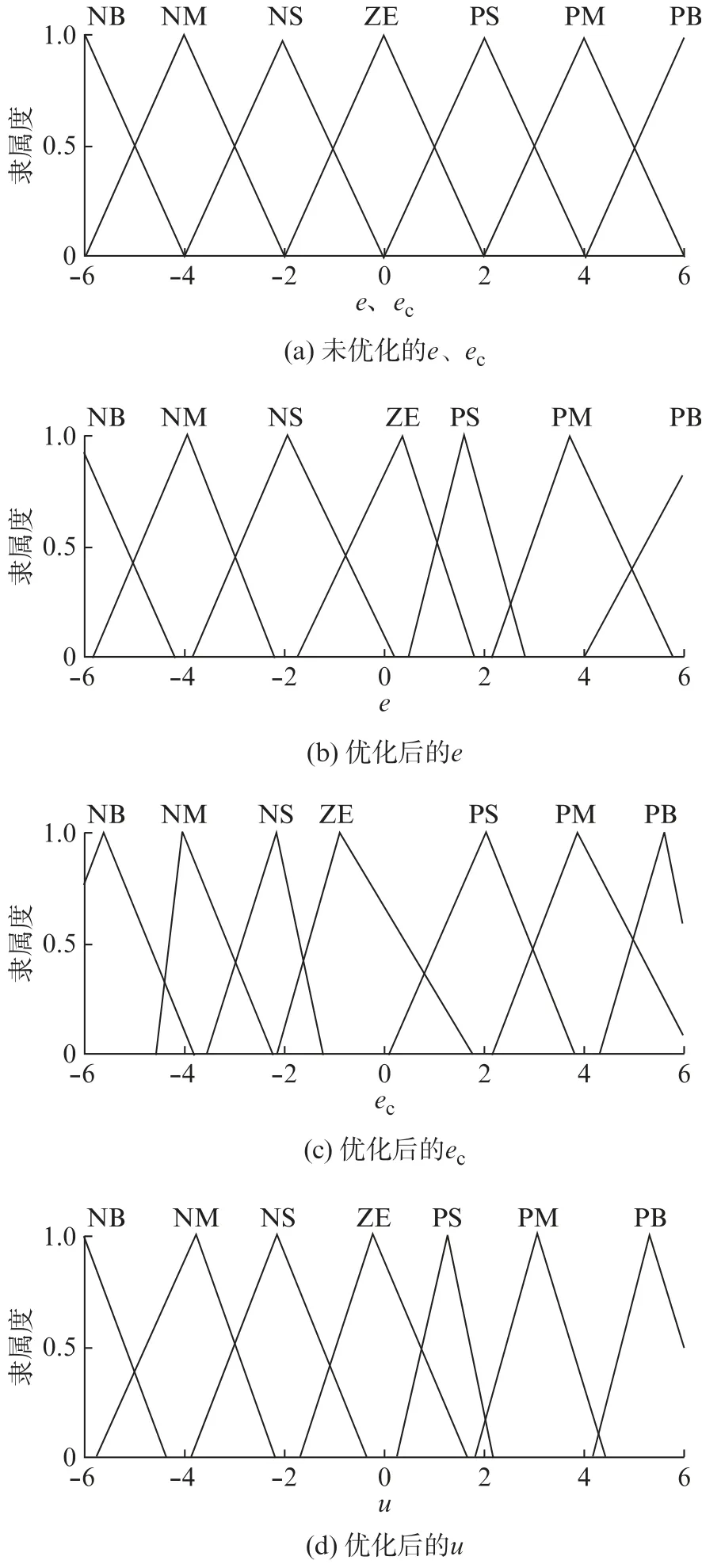
图6 改进前后隶属度函数

经过优化后的规则表如表3所示,加黑的表示优化后与优化前不同的结果。

为了证明改进后模糊控制器的优越性,本文用传统的AFD法、加入模糊控制器的AFD 法以及蚁群优化后的AFD法在同一模型中进行仿真,仿真时间为0.4 s,设置断路器在0.08 s时断开,用来模拟孤岛。仿真结果如图7所示。

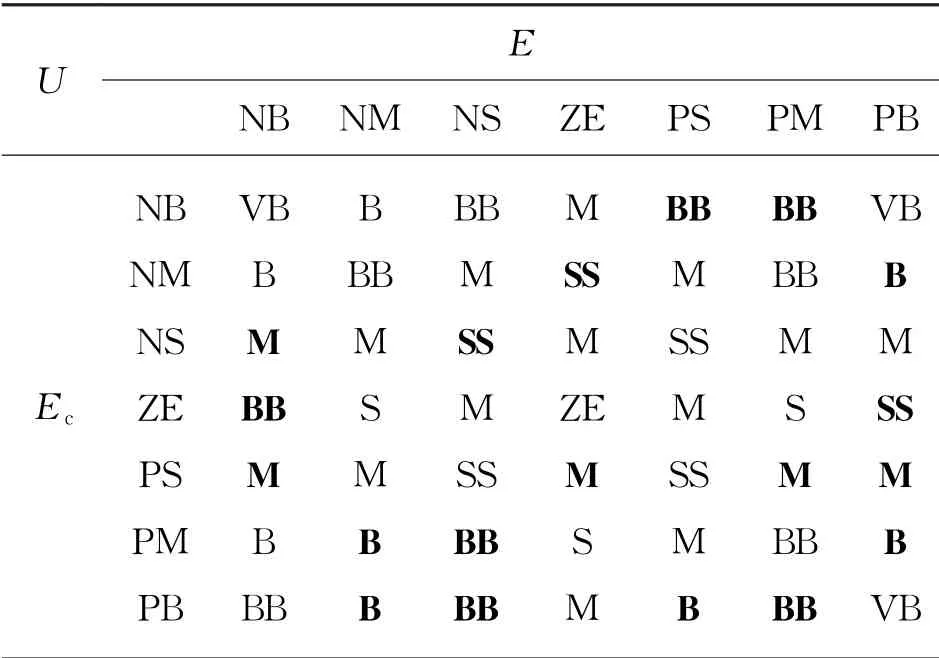
表3 优化后的模糊控制规则表

为了方便观察PCC电压与逆变器输出电流之间的频相关系,示波器输出的逆变器电流数值保持不变,将输出的PCC电压数值缩小为原来的1/8。仿真如图7所示。其中图7(a)为传统AFD 的电压、电流波形,图7(b)为传统AFD 的谐波畸变率(Total Harmonic Distortion,THD),图7(c)和图7(d)分别为加入模糊控制器后(未使用蚁群算法优化)的AFD 电压、电流波形和THD 含量,图7(e)和图7(f)分别为加入蚁群算法优化后的AFD电压、电流波形和THD 含量。具体结果如表4所示。

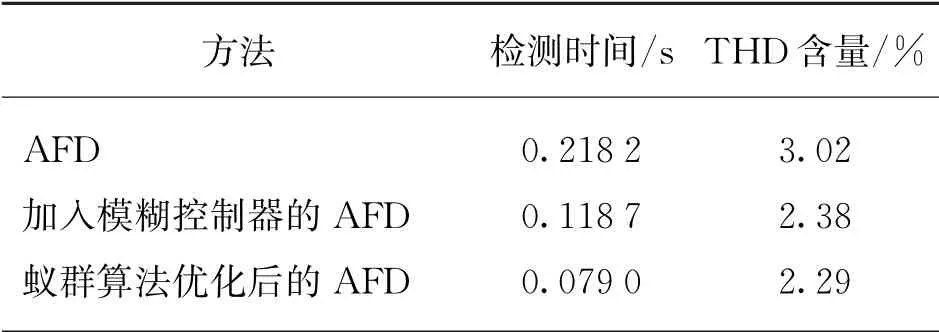
表4 仿真数据

从表4可以看出:

(1) 传统的AFD法由于检测时间超过0.2 s,无法满足IEEE—929规定;

(2) 加入模糊控制器后缩短了检测时间,并减小了逆变器电流中的THD含量;

(3) 蚁群算法优化后的模糊控制器不仅检测孤岛用时最少,对电能质量造成的影响也最小。

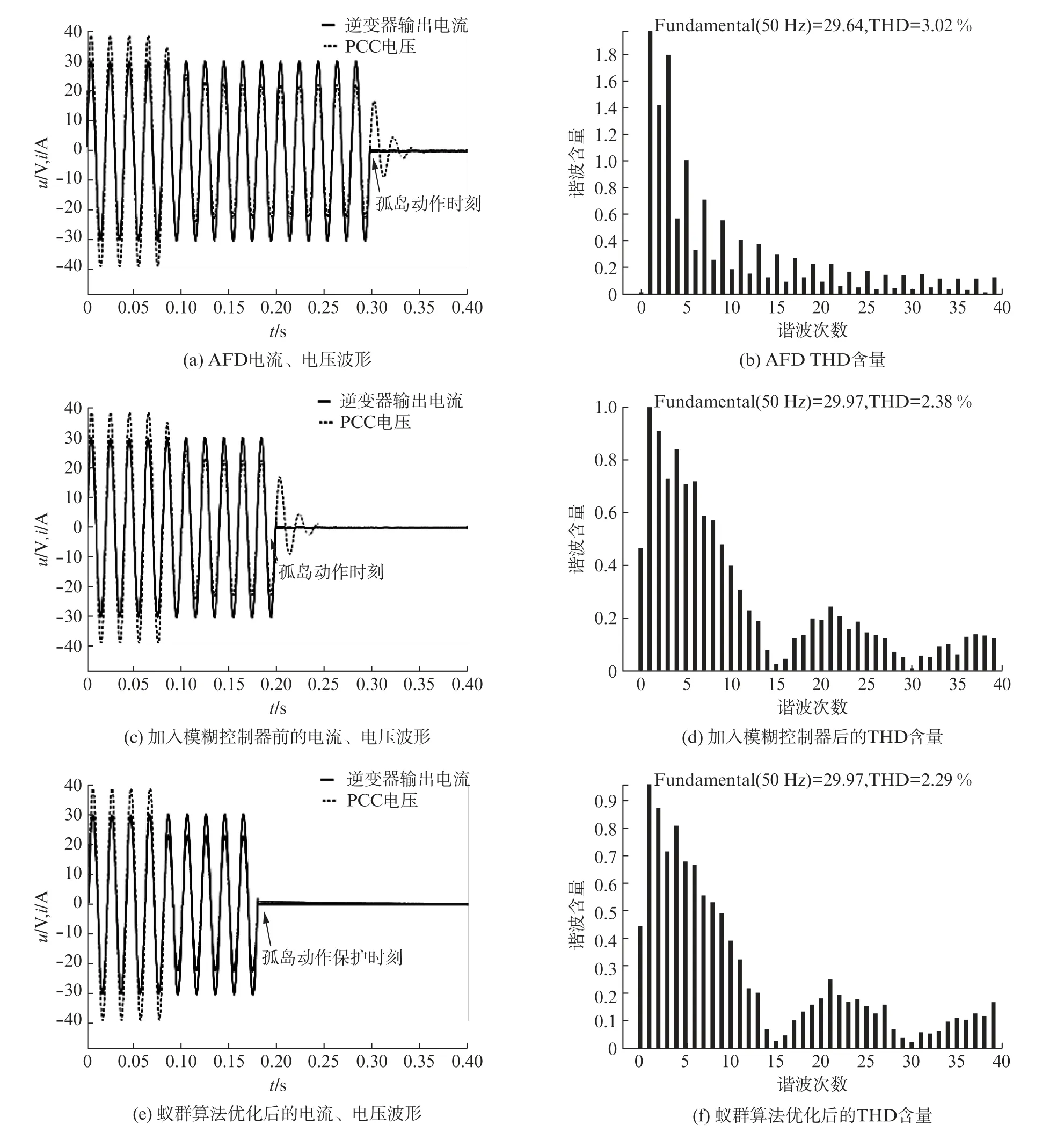
图7 3种不同方法电流电压波形和THD含量

3.2 半实物仿真分析

为了对模型合理性进行验证,采用RT-LAB半实物仿真进行了分析验证。在实验验证中,将RTLAB与DSP相结合完成半实物仿真实验。其中,RT-LAB用来模拟分布式发电并网系统,DSP28335负责采集PCC电压和电流信号,并通过算法判断孤岛信号是否产生。选用OP5330FPGA板卡输出模拟信号,OP5311FPGA 板卡输入数字信号,上位机与RT-LAB连接实现模型载入。

首先是主程序的初始化,在各变量初始化完成后,RT-LAB模拟的分布式发电并网系统处于循环等待中,即正常并网状态;接着通过设定延时时间来控制孤岛的发生时刻,从而模拟出系统的运行状态;最后判断孤岛发生,逆变器控制器输出电流为0。

实验结果如图8所示。其中图8(a)为并网0.4 s的PCC电压和逆变器输出电流波形(幅值大小已作处理)。可以看出在并网时由于PCC电位钳制作用,逆变器输出电流保持额定频率不变,周期为200 ms。图8(b)表示79 ms断网后输出波形,与图7(e)的检测时间基本一致,验证了该方法的可靠性。

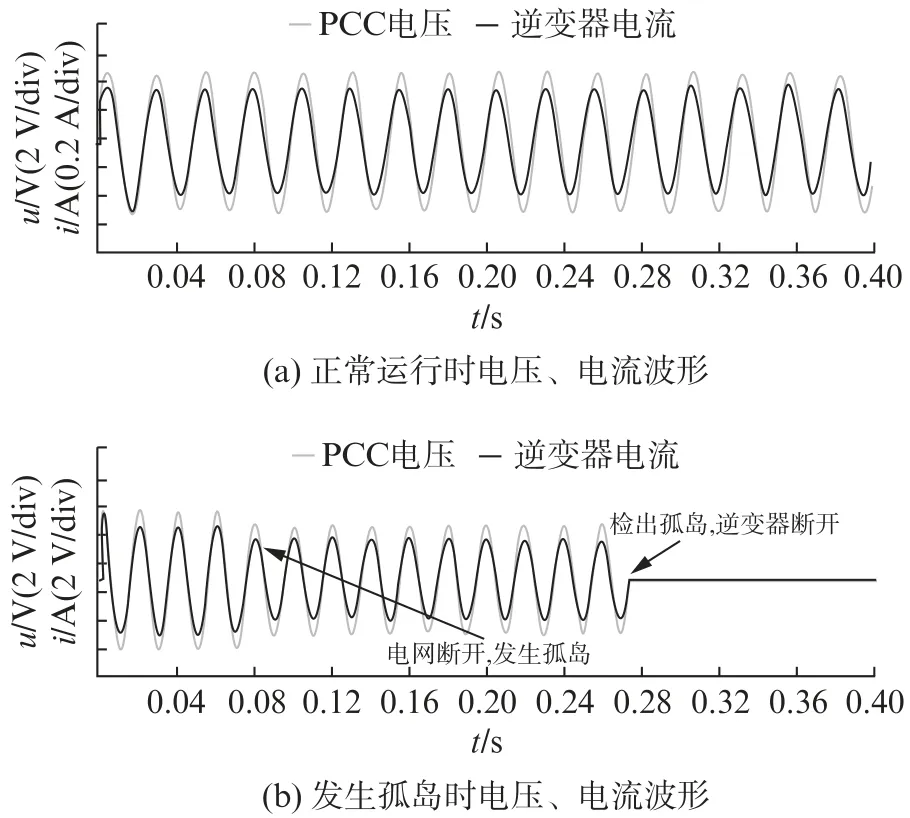
图8 实验结果

4 结 语

本文在AFD 的基础上,推导了无NDZ所需的条件,提出了对k值进行模糊优化,使它的取值能够自适应地按照制定的模糊规则调整,并采用改进的蚁群算法对模糊控制器进行进一步优化。本文通过仿真验证了所提算法的可行性:并网THD减少(低于5%的国家标准)。当负载频率同谐振频率相等的极端条件下,断网检测时间为0.079 s,并且在此负载条件下无NDZ,从而保证了分布式发电的并网可靠性。