基于新型蝙蝠算法的电动汽车停车充电优化调度
2021-05-08李春亭张体鹏朱志刚连志刚
李春亭, 张体鹏, 朱志刚, 连志刚
(上海电机学院 电子信息学院, 上海201306)
随着中国经济的快速发展,汽车已经成为越来越多家庭的必备交通工具[1-2]。汽车在给人们带来便利的同时,也带来了一系列环保问题和能源危机,电动汽车的发展可以很好地解决这些问题[3]。目前,有很多因素影响消费者对电动汽车的购买,包括消费者的经济状况、电动汽车的安全性、能耗成本等,停车位和充电设施的建设尚不完善是影响消费者购买电动汽车的主要因素。提高电动汽车停车位和充电设施的服务质量成为新能源汽车推广的关键[4]。私人充电桩存在建成后大量闲置、利用率普遍不高的现象,提高私人停车位及充电设施的利用率则成为破解停车难、充电难的新任务[5]。文献[6]引入一种智能电网环境下电动汽车协同充电模式,建立了最小化用户用电费用的最优充电模型。文献[7]将不确定优化方法应用到电动汽车充电路径优化调度中,建立了基于随机期望值的不确定优化调度模型。文献[8]基于用户对充电站的偏好程度,建立了用户对充电站的偏好表,以系统效率最大化为优化目标,对电动汽车充电调度进行研究。以上研究往往仅考虑电动汽车充电,由于充电桩所在车位也可用于停车,故停车位和充电位可协同共享,用于电动汽车停车和充电调度。将停车位和充电桩协同共享,对解决目前停车难、充电难的问题具有十分重要意义。
1 电动汽车停车充电调度
1.1 问题描述
电动汽车停车充电成本由电动汽车和停车位的状态决定[9]。电动汽车的基本状态信息包括:电池容量、服务请求类型、平均速度、当前荷电状态值、预期荷电状态值、停车时间、百公里耗电量、当前位置坐标、目的地位置坐标、适用充电桩型号。停车位的基本信息包括:充电桩型号、充电功率、停车费用、充电费用、服务费。
停车充电调度问题可描述为:区域内有s个停车充电站点,总共有m个共享车位可供电动汽车停车充电,其中包括配备充电桩的充电位和不配备充电桩的停车位。t时刻,区域内有n辆电动汽车预约停车充电,其中n辆电动汽车的预约类型和基本信息不尽相同。本文电动汽车停车充电调度的目标就是找到一种调度方案,使得n个电动汽车停车充电总费用最少。
设电动汽车i到停车位j进行停车充电的成本为Cij,电动汽车i是否到停车位j进行停车充电的布尔变量为

n辆电动汽车进行停车充电的总成本为
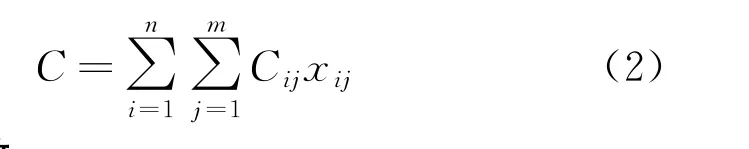
1.2 目标函数
所有电动汽车停车充电成本C由所有电动汽车从当前位置到目标停车位的电量耗费、充电费用、停车费用和服务费构成,即
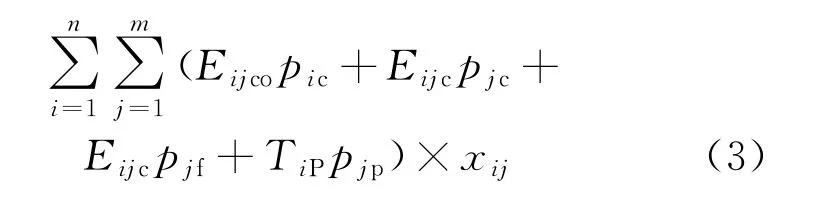
式中:E ijco为电动汽车i从发出请求地到停车位j的耗电量;p ic为电动汽车i现有上一次充电的充电单价;E ijc为电动汽车i的充电量;p jc为停车位j充电桩的充电单价;p jf为停车位j单位充电量的服务费;p jp为充电桩j的停车单价;T ip为电动汽车i的停车时长。
其中,电动汽车i从发出请求地到停车位j的耗电量
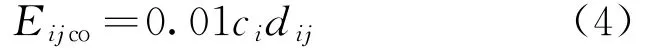
式中:c i为电动汽车i的百公里耗电量;d ij为电动汽车i从发出请求地到停车位j的路程。
1.3 约束条件
为了达到优化调度目标,要充分考虑所有电动汽车的预约类型和状态信息,还要考虑预约用户的停车时长,在为所有电动汽车分配合适的停车位的基础上使所有电动汽车停车充电总费用最少。
(1) 对于所有发出请求的电动汽车用户,其车辆剩余电量均能到达停车充电管控系统为其分配的停车位,即

式中:Soc,i为电动汽车i的电池剩余电量百分比;Soc,ij为电动汽车i到停车位j需消耗电池电量百分比。
(2) 对于仅充电用户和停车充电用户,停车充电管控系统为其分配的停车位j配备有充电桩,且所配备充电桩与电动汽车i型号相符,即

式中:Si为电动汽车i的型号;Sj为停车位j上充电桩可以匹配的车辆型号。
(3) 对于仅充电的电动汽车用户,电动汽车i的排队等待时间以及充电所用时间在车主可接受的限度以内,即

式中:T iw为车主iper能接受的最大等待时间;T ijw为车主iper的等待时间;T ijc为电动汽车的充电所用时间。
(4) 对于仅停车的电动汽车,电动汽车i的车主iper从停车位j步行至目的地的时间耗费在用户可接受的时间限度之内,即

式中:T1为电动汽车i的车主iper最大能接受的从停车位j步行至目的地的时间耗费;T2为电动汽车i的车主可接受的最长时间。
2 算法设计
2.1 新型蝙蝠算法的数学模型
蝙蝠算法是由Yang提出的一种高效生物启发式算法,在准确性和有效性方面远优于其他算法,且大部分参数无需调整[11],故本文采用蝙蝠算法来优化电动汽车停车充电费用最小优化调度问题。针对蝙蝠算法易陷入局部最优和过早收敛的问题,提出了一种局部搜索和全局搜索相结合的新型蝙蝠算法。
假设在一个d维的目标搜索空间中,有一个蝙蝠种群包括n只虚拟蝙蝠。t时刻,种群中蝙蝠i的频率、速度和位置分别为和为当前时刻整个蝙蝠种群搜索到的最优位置为当前时刻蝙蝠i的历史最优搜索位置为当前种群搜索到的最优位置。t+1时刻,第i只蝙蝠位置更新至,速度更新为在新型蝙蝠算法中,蝙蝠个体对自身频率、速度、位置的更新[12]如下:
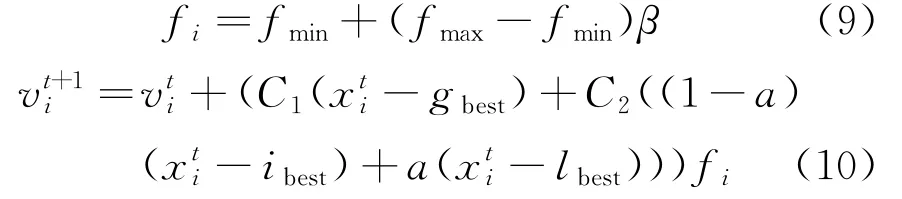
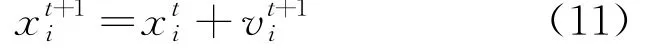
式中:fmax为蝙蝠最大脉冲频率;fmin为蝙蝠最小脉冲频率;β为[-1,1]内的随机数;C1、C2为学习因子,C1取值区间为[0.1,2]的一个常数,C2为取值区间[-1,2]的一个常数,本文均取2;a为取值区间[0,1]之间的一个常数,本文取值为0.8。
本文提出的新型蝙蝠算法通过4部分来更新蝙蝠i的速度:蝙蝠i前一次迭代时的速度;蝙蝠i当前位置与当前历史种群最优位置之间的距离;蝙蝠i当前位置与前一次迭代时种群内最优蝙蝠位置之间的距离;蝙蝠i当前位置与蝙蝠i的历史最优位置之间的距离。
2.2 新型蝙蝠算法的实现步骤
假设求f(x)的最小值,种群数量为n,迭代次数为N。新型蝙蝠算法的基本实现步骤如下:
(1) 蝙蝠种群初始化,在d维空间中,扩散分布一组初始解[13]。最大脉冲响度A0,最大脉冲率R0,搜索脉冲频率范围[fmin,fmax],音量的衰减系数α,搜索频率的增强系数γ,搜索精度ε和最大迭代次数N。
(3) 蝙蝠的搜索脉冲频率、速度和位置根据式(9)~(11)进行更新。
(4) 生成均匀分布随机数r1,蝙蝠i的脉冲频率为r i,如果r1>r i,则对当前最优解进行随机扰动,产生一个新的解,并对新解进行越界判断。
(5) 生成均匀分布随机数r2,如果r2<A i,且f(x i)<f(x*),则接受(4)产生的新解,然后更新脉冲响度A t和脉冲发射速率Rt。
(6) 对所有蝙蝠的适应度值进行排序,找出当前的全局最优解和最优适应值。
(7) 对当前种群内所有蝙蝠的适应度值进行排序,找出当前种群的最优蝙蝠个体
(9) 重复(2)~(5)直至满足设定的最优解条件或者达到最大迭代次数。
(10) 输出全局最优值和最优解。
2.3 编码和解码策略
蝙蝠算法最初采用实数编码来优化连续函数[14],蝙蝠在d维空间中的存在形式x2,…,x j,…,x d],其中,x j为蝙蝠在d维空间中的第j个维度上的分量,x j∈R(j=1,2,…,d)。电动汽车停车充电调度问题的解分布在离散空间内,使用蝙蝠算法求解电动汽车停车充电调度优化问题,首先需要考虑编码和解码问题,将实数编码转化为自然数编码[15]。
在实际问题中,车位数量大于电动汽车数量,即m>n,设蝙蝠所处的空间维度为d,且d=m。将停车位编号固定,对停车位进行编码,则编码长度为停车位的数量m,编码形式p m]。其中,1~m为停车位编号,各停车位上的编码表示该停车充电调度方案对应的停车位上的电动汽车编号。
由于停车位数量多于发出停车充电请求的电动汽车数量,此时部分停车位上没有电动汽车前来停车充电。在进行编码时,假设有m辆电动汽车发出停车充电请求,区域内有m个停车位为其提供停车充电服务,对于匹配到编号为n+1~m的电动汽车的停车位,其实际情况为该停车位上没有电动汽车前来停车充电,所以将该停车位上的电动汽车编号置空,即可得到m个停车位的编码[p1,p2,…,p i,…,p m],即本文电动汽车停车充电问题中各停车位上进行停车充电的电动汽车编号。
关于5辆电动汽车,8个停车位的泊位问题,从实数到自然数的编码转化过程如表1所示。

表1 编码和解码策略
蝙蝠各维度表示停车位的编号,蝙蝠Y各维度上的分量表示在该停车位上停车充电的电动汽车编号,5辆电动汽车到8个停车位停车充电的指派关系如表2所示。

表2 电动汽车到停车位停车充电的指派关系
3 仿真实验
设区域内共有10个停车充电站点,包括商场、私人小区、学校和单位等。将10个站点分别编号为S1,S2,…,S10,设每个站点有10个共享车位,包括停车位和充电位,则该区域内共有100个共享车位,其编号分别设为P1,P2,…,P100。某时段,该区域内有50辆电动汽车发出停车充电请求,并将其编号设为E1,E2,…,E50,50辆电动汽车的位置坐标分别为I1,I2,…,I50,目的地坐标分别为D1,D2,…,D50。100个共享车位和50辆电动汽车的基本信息使用Matlab随机生成。
编写基于所有电动汽车停车充电费用最少模型的优化调度程序,使用经典蝙蝠算法与本文提出的新型蝙蝠算法对所有电动汽车停车充电费用最少调度模型进行优化,获得最优停车充电调度方案。为验证本文提出的新型蝙蝠算法的优越性,两种算法设置相同的参数,种群规模均设置为200,最大迭代次数均设置为2 000。通过仿真测试,两种算法下50辆电动汽车停车充电费用的变化情况如图1所示。
由图1可知,经典蝙蝠算法在迭代到100代时陷入局部最优,在迭代到600代时跳出局部最优,逐步接近最优值,优化得到50辆电动汽车最小停车充电费用为102.883 5元;本文提出的新型蝙蝠算法在迭代到400代时接近最优值,收敛速度更快,且优化得到的50辆电动汽车最小停车充电费用为68.430 6元,比蝙蝠算法优化得到的最小停车充电费用少34.452 9元。使用蝙蝠算法和新型蝙蝠算法优化50辆电动汽车停车充电费用最少调度方案分别如表3和表4所示。
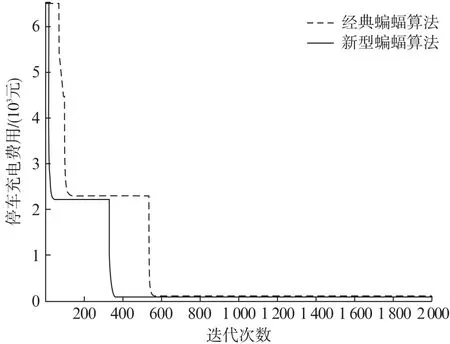
图1 停车充电费用最少调度方案寻优过程
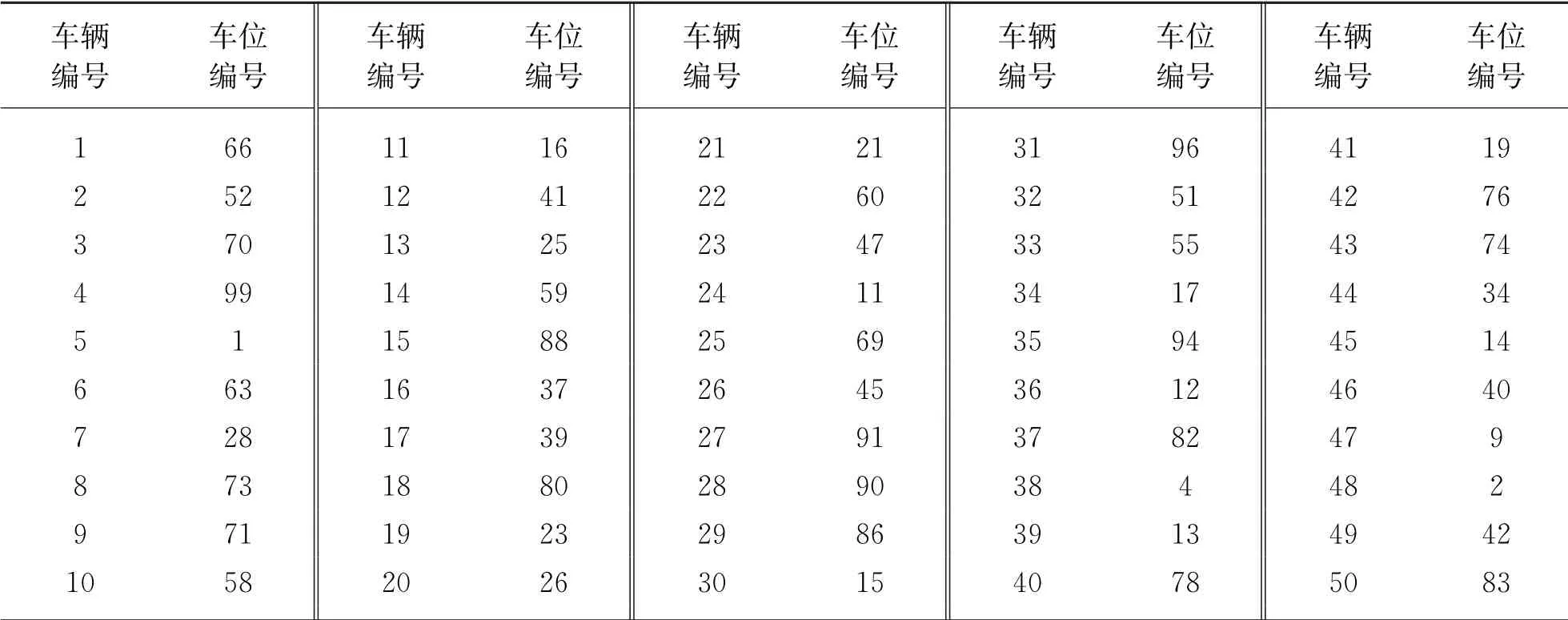
表3 基于蝙蝠算法的费用最少停车充电调度方案
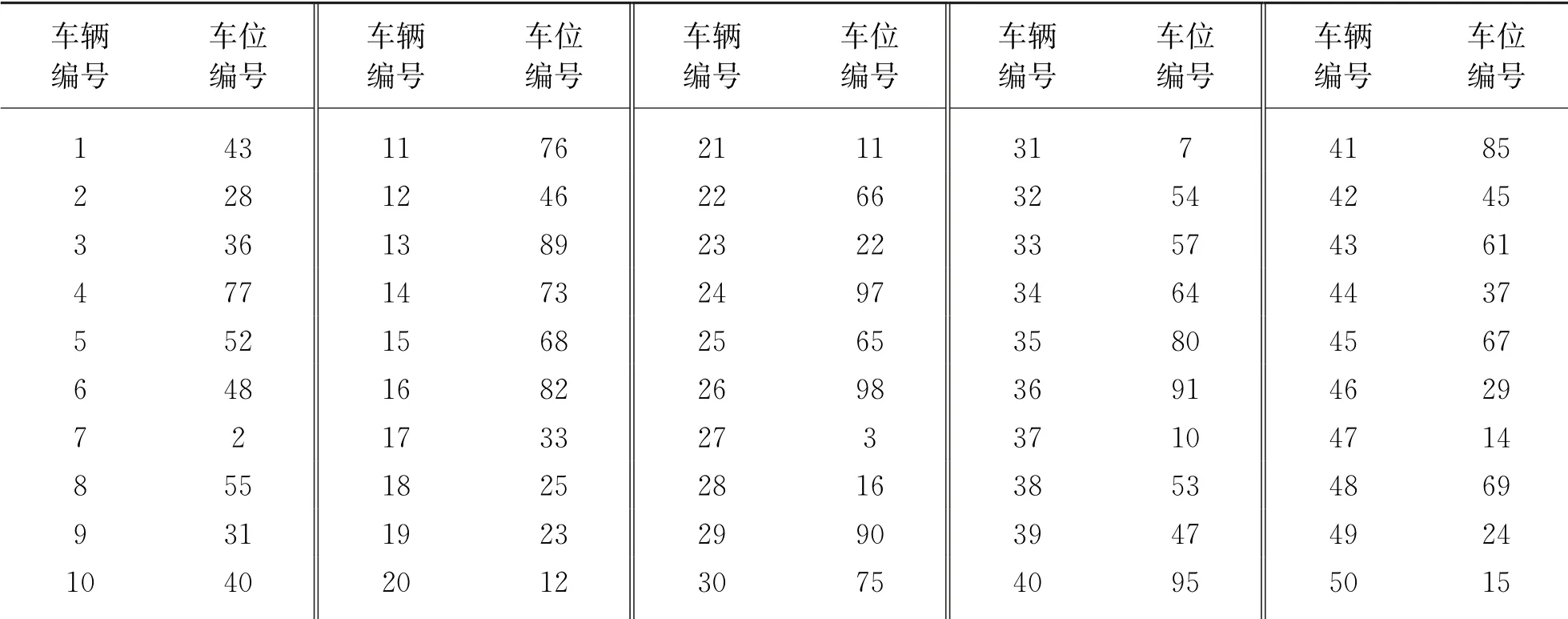
表4 基于新型蝙蝠算法的费用最少停车充电调度方案
由两种算法的仿真结果可知,蝙蝠算法和新型蝙蝠算法均可优化得到所有电动汽车停车充电费用最少调度方案;且新型蝙蝠算法优化得到的最优调度方案停车充电费用更少。
4 结 语
本文基于停车位和充电桩共享,建立了所有电动汽车停车充电费用最少调度模型,为电动汽车停车充电调度问题提供了理论依据。使用蝙蝠算法和本文提出的新型蝙蝠算法优化电动汽车停车充电费用最小调度模型,证明了本文电动汽车停车充电优化调度模型的可行性,且提出的新型蝙蝠算法具有较高的搜索精度和收敛速度。
